不同突觸的神經元網絡同步放電比較研究

劉瑾琬

（蘭州交通大學，蘭州 730070）

人腦中的神經系統是一個非常復雜的多功能系統，由千億個神經突觸連接的神經元構成，具有復雜的網絡動力學行為，是生物信息的進行傳遞、整合與協調的中樞， 為研究神經系統放電活動和信息行為提供了新的角度。研究神經網絡的放電過程，有助于探究神經信息編碼機制，是腦科學研究領域的重要內容[1]。

Stevens 等[2-3]研究發現，神經元之間放電序列的相關性和同步放電現象可以有效抑制噪聲對編碼的影響，提高編碼效果，保證神經信息編碼的可靠性。 常小龍等[4]采用FHN 神經元作為網絡節點搭建了神經元網絡，通過數值模擬的方法，研究并討論了神經網絡的同步放電特性，并對其與抗擾能力進行了分析計算。上述研究從神經信息處理角度研究了神經系統同步放電機制，但是研究中選用的多為較低維度的神經元模型，不能精確模擬真實神經元電生理特性。

本文選取最接近生物學實際的Hodgkin-Huxley（ HH）模型，基于MATLAB&Simulink 平臺，采用數值模擬的方法分別搭建由電突觸和化學突觸連接的具有生物特性的復雜神經元網絡， 對比分析了神經突觸對神經元網絡的同步放電特性的影響。

1 研究方法

1.1 Hodgkin-Huxley 模型

HH 模型在1952 年由Hodgkin 和Huxley 提出[5-8]，通過一組四階非線性微分方程描述了烏賊軸突細胞膜動作電位產生和傳導的過程， 能夠準確地解釋實驗結果，如式（ 1）所示

式中：I 為外部刺激電流，C 為細胞膜單位面積的電容，值為1 μV/cm2；V 是膜電壓， 初值-65 mV；GNa和GK分別代表鈉離子通道、鉀離子通道的最大電導，值分別為120 mS/cm2、360 mS/cm2；GL為漏電導，值為0.3 mS/cm2；ENa、EK、EL分別為鈉離子通道、鉀離子通道、漏電流的反轉電勢，值分別為50 mV，-77 mV，-54.5 mV；m 和h分別為鈉離子通道電導的激活變量和抑制變量，n 為鉀離子通道的激活變量，α 和β 是與膜電位有關而與時間無關的速率函數。

1.2 突觸模型

大腦神經系統中信號的傳遞、整合的過程需要依賴神經突觸連接構成的神經回路。神經突觸作為神經元之間相互聯系并通信的部位， 包括電突觸和化學突觸2類。 化學突觸廣泛存在于生物體神經系統中，電突觸是一種簡單的神經元之間的電耦合關系，一般存在于低等動物的神經系統中。 電突觸數學模型如式（ 2）所示

式中：Isyn為電突觸耦合電流，g 為突觸耦合強度，V 為突觸前神經元動作電位，V1為突觸后神經元動作電位， 此電流為突觸前神經元對突觸后神經元通過電突觸耦合產生的突觸電流。

Savtchenko[9]研究并提出了一個復雜的動力學模型， 該模型能夠精確描述化學突觸進行信息傳遞的過程且更接近于生物學實際， 故本文選取該化學突觸模型，其表達式如式（ 3）所示

式中：Isyn為突觸后電流，GS為突觸后電導，ES為突觸可逆電位，VP為突觸后保持電位，V1、V2分別為前后神經元的膜電位，-CmS2描述了突觸前神經元動作電位產生的電容電流，GS（ VP-ES+V1-V2）描述了通過突觸后配體門控通道的離子電流。

由Leonid 化學突觸連接的2 個HH 神經元數學模型如式（ 4）

式（ 4）說明了通過Leonid 化學突觸耦合的神經元中神經元膜電位和突觸電流之間的數學關系。 用其來描述由多個單神經元構成的具有非線性相互作用的復雜網絡。式中：i 和j 表示網絡中神經元的編號。根據所得到的數值解可以計算出不同情況下的膜電壓和相應的突觸電流。 這個耦合系統方程為單個神經元膜電位方程右側增加一項突觸電流Isyn（ j，i）。 在方程中i 是突觸前神經元，j 是突觸后的神經元。 突觸電流的數值是由前后神經元膜電位確定的， 且突觸電流的流向是j 到i，即突觸電流僅對突觸后神經元產生影響。 每一個神經元都能接受刺激信號Iext而不產生任何影響，在神經元僅傳導刺激，沒有外界電流刺激的情況下，對應的Iext值為0。 A（ i，j）是取1 或者0 的連接矩陣，值是1 說明神經元j 和神經元i 存在連接，否則，說明2 個神經元之間沒有聯系；Gji是突觸后的電導。

由電突觸連接的2 個HH 神經元數學模型如式（ 5）所示

式中：i、j 是網絡中的神經元的編號，Iext表示外部刺激電流的大小。前、后膜電位的差值與縫隙電阻相乘取得突觸電流值，突觸電流作用于2 個互相耦合神經元。

通過建立HH 神經元和突觸耦合的數學模型，為神經元網絡仿真建模提供了依據。 本節通過對耦合系統數學模型進行分析， 為后文通過軟件對生物神經元網絡進行數值模擬做好了鋪墊。

1.3 模擬仿真平臺

本文基于MATLAB&Simulink 平臺進行建模仿真。分別由化學突觸和電突觸耦合的神經元Simulink 模型如圖1 所示。

圖1 雙神經元耦合的Simulink 建模

如圖1 所示神經元和突觸模塊進行了封裝處理，在構建神經元網絡模型的過程中， 如需增加神經元個數或調整神經元網絡的拓撲結構時， 封裝好的神經元和突觸可根據對應拓撲結果直接連接。 本文在構建神經元網絡模型時，采用模塊化建模，能直觀地反應所建網絡模型各模塊之間的相互關系。

2 研究結果

在大腦的神經系統中， 神經元網絡的連接方式分為規則連接和不規則連接，實驗結果表明，真實的生物神經元網絡以不規則連接方式為主， 表現為小世界特性。本文通過構建小世界神經元網絡，比較研究了分別由電突觸和化學突觸連接的小世界神經元網絡在同一正弦信號刺激下的同步放電特性。

本文構建的神經元網絡模型中神經元個數為5，且為全同神經元。 網絡中神經元通過化學突觸依次有向連接，符合生物神經系統中信息傳遞結構。以化學突觸連接的簡單環網和小世界網絡為例， 在Simulink 中構建的模型如圖2 所示，圖中Synapse（ 1，2）表示神經元N1 和N2（ 后文神經元均由編號表示）之間的化學突觸，信息由N1 向N2 傳遞。 小世界神經元網絡是在簡單環網模型結構的基礎上， 不破壞原來環結構的任意一個連接，對網絡進行加邊處理，且神經元本身不能自連。 小世界神經元網絡模型中每個神經元依序與網絡中除自身外其他2 個神經元相連， 該模型在簡單環網的基礎上增加了10 條突觸，符合小世界網絡特點。 神經元網絡的輸入信號為正弦波信號Iext=10sin（ 0.1πt）+10，N1 接收刺激信號，其余神經元外加刺激為0，突觸后電導（ 耦合強度）取值設置為1 mS/cm2。

圖2 化學突觸連接的5 神經元網絡Simulink 模型

將正弦信號Iext=10sin（ 0.04πt）+10 作為刺激信號輸入神經元網絡，正弦信號時域波形圖如圖3 所示。神經元網絡中N1 接收刺激信號， 其余神經元外加刺激為零，設置仿真時間t 為100 ms。 圖4 為示波器模塊觀測的由電突觸和化學突觸連接的神經元網絡中N1 和N5 的動作電位波形。

圖3 正弦信號時域波形圖

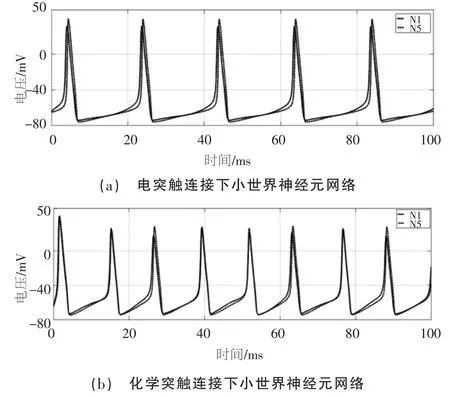
圖4 不同突觸連接下小世界神經元網絡同步放電效果

由仿真結果可以看出， 相同拓撲結構的神經元網絡在同一刺激信號下， 神經元都產生了穩定的周期電位，均包含完整的放電過程。電突觸連接的神經元網絡N1 和N5 動作電位會產生時延，最大時延為1.5 ms；化學突觸連接的神經元網絡N1、N5 動作電位時延較小，最大時延為0.5 ms，且放電波形不斷趨于重合，同時，當輸入信號不變， 化學突觸連接的神經元網絡放電頻率提高但依然保持節律性。

3 結論

本研究采用數值模擬的方法， 選取Hodgkin-Huxley 神經元作為神經元網絡的基本單元， 分別構建了由電突觸和化學突觸連接， 符合生物學實際的小世界神經元網絡。 對不同類型神經突觸連接的神經元網絡同步放電特性進行了對比研究。研究結果發現，在同一外加信號的刺激下， 分別由電突觸和化學突觸連接的具有相同拓撲結構的神經元網絡具有不同的同步放電特性。 電突觸連接的神經元網絡動作電位會產生時延，最大時延為1.5 ms；化學突觸連接的神經元網絡動作電位時延較小， 最大時延為0.5 ms， 且基本趨于同步。證明在同一刺激信號，相同拓撲結構的神經元網絡中， 化學突觸連接的網絡同步放電特性要優于電突觸連接的神經元網絡。同時，突觸類型的不同可能會改變神經信息的編碼方式但不會改變信息傳遞的可靠性。本文基于Hodgkin-Huxley 神經元模型，構建了具有生物屬性的神經元網絡， 考慮了真實神經系統中通過電突觸和化學突觸進行信息傳遞的過程， 這對后續研究神經信息傳遞的相關機制提供了一定的便利， 為大腦記憶功能的神經生物學機制提供了實驗方法。