配電網(wǎng)分布式電源和儲能協(xié)調(diào)控制方法研究

車紫瑩

（國網(wǎng)福建省電力有限公司 泉州供電公司，福建 泉州 362000）

0 引 言

能源的清潔高效利用離不開高水平的電氣化，技術(shù)進步和成本下降必然會導(dǎo)致大規(guī)模的分布式電源并網(wǎng)，然而分布式電源由于其自身的特性，會對電網(wǎng)的穩(wěn)定性造成影響[1-4]。針對這些問題，提出了一種新的基于分解的多目標(biāo)優(yōu)化算法，基于算法對多目標(biāo)協(xié)調(diào)控制策略進行求解，最后在MATLAB 平臺上驗證了本研究的可行性和有效性[5-8]。

1 基于模糊理論的分布式電源出力

本研究中考慮的是風(fēng)電模型，其模型表示為

式中：Pw,random為隨機調(diào)度模型；Pw,fuzy為模糊調(diào)度模型。

Pw,random的大小主要受風(fēng)速影響，風(fēng)速密度均值函數(shù)可以表示為

式中：s為尺度系數(shù)；v為實際的風(fēng)速大小；k為用來描述f(v)形狀的值，一般在[1.8,2.8]內(nèi)取值。Pw,random的具體表達式為

式中：vi、vo、vr為切入、切出與額定風(fēng)速；Pr為額定輸出功率。

在調(diào)度周期內(nèi)，Pw,fuzy相對應(yīng)的隸屬度函數(shù)可以表示為

隸屬度函數(shù)的形狀由隸屬度參數(shù)Pw1～Pw4決定，而參數(shù)Pw1～Pw4的取值公式為

式中：wk為比例系數(shù)，大小取決于風(fēng)電出力的歷史數(shù)據(jù)；Pfc為風(fēng)電出力的預(yù)測值。梯形模糊參數(shù)可被表示為

2 儲能充放電模型

充電過程為

放電過程為

式中：SOC(t)和SOC(t+Δt)分別為t、t+Δt時刻所儲存的電量；Δt為時間間隔；ε為系統(tǒng)的剩余損失電量率；SOCchg(t+Δt)和SOCdis(t+Δt)為電池儲能系統(tǒng)（Battery Energy Storage System，BESS）在t+Δt時刻的充放電功率，效率分別由α和β決定；SOCe為系統(tǒng)儲能容量。

3 儲能控制策略

本研究的儲能設(shè)備選定為鈉硫電池，并且考慮峰谷分時電價，儲能控制策略的流程主要針對2種情況：（1）負(fù)荷大于分布式電源出力；（2）負(fù)荷小于分布式電源出力。當(dāng)負(fù)荷大于分布式電源出力時，需要分布式電源和配電網(wǎng)同時提供電能；當(dāng)負(fù)荷小于分布式電源出力時，僅需要分布式電源提供電能。

4 多目標(biāo)協(xié)調(diào)控制策略

4.1 日成本

儲能調(diào)度成本為

式中：KESS為系統(tǒng)單位調(diào)度成本；和為t時段內(nèi)第m個系統(tǒng)的充放電功率。

風(fēng)電發(fā)電成本為

棄風(fēng)懲罰成本為

式中：Pwf(t)為系統(tǒng)被消納的發(fā)電總量；ec(t)為風(fēng)電上網(wǎng)電價。

微燃機發(fā)電成本為

式中：NG為總機組數(shù)；機組啟停狀態(tài)由h1,t確定；為l機組在t時刻的有功輸出；同l機組的燃耗系數(shù)由a1、b1和c1共同確定。

微燃機啟動停止成本為

式中：B1,t為當(dāng)前l(fā)機組的啟動停止成本。

4.2 日效益

電價效益為

式中：ed(t)、ew(t)分別為用戶分時電價和風(fēng)電補貼電價；Pe(t)、Pd(t)、Pw(t)分別為系統(tǒng)上網(wǎng)功率、用戶負(fù)荷功率以及風(fēng)機出力。

環(huán)境效益為

式中：m為風(fēng)電總個數(shù)；n污染物的種類個數(shù)；HsCP、HsMG,j分別為火電機組第s項污染物排放總額和第j個風(fēng)電第s項污染物的排放總額；Ve,s為第s項污染物減排價值。

節(jié)能效益為

式中：Mc為共消耗煤炭總額；pc為單價；Pw,j為第j個系統(tǒng)發(fā)電總量。

4.3 目標(biāo)函數(shù)

本研究基于模糊理論提出了一種新的多目標(biāo)協(xié)調(diào)控制策略，控制目標(biāo)如下：目標(biāo)函數(shù)定義為日凈利潤PPRO的最大化函數(shù)，綜合前面的日成本和日收益，PPRO最大值為

5 多目標(biāo)協(xié)同控制策略求解算法

MOEA/D 算法的流程如圖1 所示。為了克服最優(yōu)前沿形狀的不確定性，本研究基于切比雪夫分解法分解多目標(biāo)優(yōu)化問題[9,10]，其數(shù)學(xué)表達式為

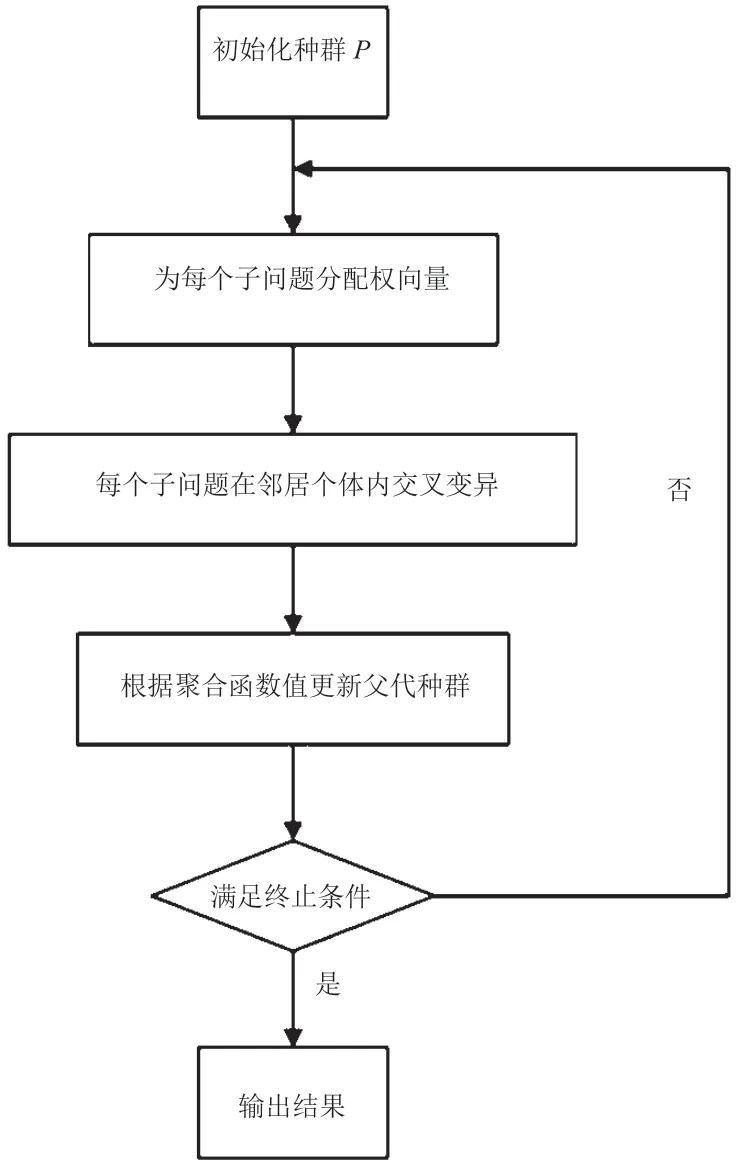
圖1 MOEA/D 算法的基本流程

式中：m為目標(biāo)函數(shù)數(shù)目；z*={z1*,…,zm*}T為參考點；λ={λ1,…,λm}為權(quán)重向量。

6 仿真驗證

文章選擇改進后的IEEE33 節(jié)點電力系統(tǒng)作為研究對象，如圖2 所示。

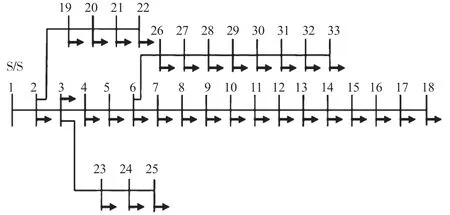
圖2 IEEE33 節(jié)點配單網(wǎng)系統(tǒng)

仿真后得到的并網(wǎng)前后負(fù)荷需求對比如圖3所示，可以清晰地看到，并網(wǎng)后負(fù)荷的需求、波動、峰谷差相較并網(wǎng)前都有明顯降低，并且有良好的削峰效果。另外，儲能并網(wǎng)改變了負(fù)荷峰值出現(xiàn)的時間，降低了配電網(wǎng)的備用容量。以上手段能夠降低負(fù)荷的波動性，提高經(jīng)濟效益。

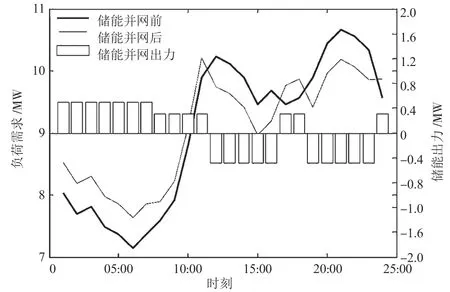
圖3 儲能并網(wǎng)前后的負(fù)荷需求

7 結(jié) 論

本研究的研究對象為風(fēng)力分布式電源，將電源處理作為模糊變量并建立了相應(yīng)的可信性分布函數(shù)及隸屬度函數(shù)；提出系統(tǒng)充放電模型并制訂了相應(yīng)的儲能控制策略。另外，基于所給出的IEEE33 節(jié)點電力系統(tǒng)，在MATLAB 平臺上進行策略有效性驗證。