無人工程機械路徑規劃算法應用

楊夏寧　黃位偉　李志恒　玉海韓

關鍵詞：無人裝載機；路徑規劃；AGV；土方機械；路徑沖突

中圖分類號：TP18 文獻標識碼：A

文章編號：1009-3044（2023）21-0024-04

0 引言

工程機械是體現國家高端制造水平的一個重要指標，目前我國的工程機械發展水平面臨著前所未有的挑戰。其中，核心技術不足，數字化和智能化發展落后是主要的原因。融入現代化信息技術，使機械設備向著更高端的自動化、智能化系統發展，推進“5G + 工程機械”模式[1]的發展是目前研究的重點之一。

近年來隨著物流技術的發展、5G通信技術的成熟和人工倉儲成本的提高。以AGV（AutomatedGuided Vehicle，AGV） 自動物料轉運小車為代表的倉儲自動調度和路徑規劃算法發展迅速，無人物流倉儲通過裝備分揀系統，極大地提高了現代物流的效率，進一步提高了自動化和智能化程度。AGV無人倉儲作業的成功帶動了各行業中無人作業的發展，相關技術的應用也不再局限于物流行業[2-3]。AGV路徑規劃問題一般分為全局路徑規劃和局部路徑規劃兩步。全局路徑規劃從全局出發，不考慮動態變化規劃出符合全局的最優路徑；后者則實時地更新自身運行狀態，實現動態地避障功能。目前常用的全局規劃算法主要是A*算法[4]、粒子群算法[5]和蟻群算法[6]。局部規劃常用的算法有動態窗口法[7]和人工視場法[8]。路徑規劃一般以路徑距離代價作為主要的代價函數，計算得到的路徑雖然是最短的，但是并不一定是最優的。

工程機械行業作業環境和自身運行狀態復雜，對路徑規劃的影響都很大。單純的以路徑距離代價作為總代價函數無法滿足復雜的工程問題。為了改善規劃算法在工程機械及相關領域的應用，本文結合全局規劃和局部規劃算法，對固定作業場景的裝載機倒料場景進行柵格化和拓撲化，采取A*算法尋找最短路徑，并通過CBS（Conflict Based Search， CBS）算法[9]解決路徑沖突問題，從而找到全局最優路徑，并基于路徑距離代價，考慮裝載機滿載和空載運行代價，面向不同的工況進行仿真實驗，以提高算法的魯棒性。

1 問題描述

為具象化算法的應用效果，本文將路徑規劃算法應用到實際的裝載機裝卸料固定作業場景中。結合實際生產需要和裝載機運行條件對場景進行建模，分析算法的可行性。

1.1 場景描述

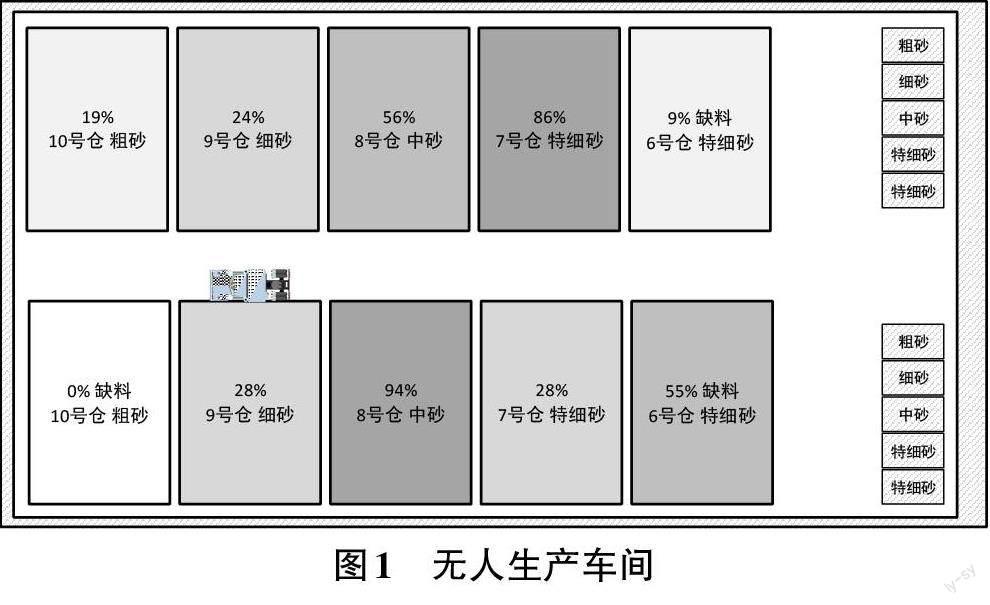
無人裝載機裝卸料任務在10個料倉和10個漏斗之間完成。由于場地空間的限制和對安全的考慮，裝載機在作業現場行駛的過程中不允許并行，所有的道路都是單行道，圖1是無人生產車間示意圖。

無人生產車間包括裝載機運行通道、粗砂倉庫和粗砂漏斗各4個、中砂倉庫和中砂漏斗各2個、特細砂倉庫和特細砂漏斗各4個。為了滿足生產需要，裝載機需要不斷地從料倉中運送砂料到漏斗，如何在規定的時間內高效地完成任務是本文方法要解決的主要問題。

多車任務調度規劃問題是一個復雜的問題，通常對物料轉運車的分配原則主要有最短路徑原則、最短工作時間原則、工作任務優先級原則和綜合指標的原則[10]。考慮到裝載機造價昂貴，且作業現場空間受限，安全代價大。本文通過采用雙車模型對路徑規劃問題進行求解，并對無人生產車間做出以下約束：

1） 通過嚴格限制作業場景動態信息，將作業場景固定，場景信息已知。裝載機可行走的道路固定不變，車輛路徑都為單行道。

2） 裝載機在漏斗和料倉的作業時間固定為t ∈ （t₁，t₂），時間參數由裝載機性能參數決定。

3） 兩臺裝載機的型號、速度等運行參數完全一致。

由于大型機械滿載和空載期間的運行狀態差異較大，場景描述除了對場景做出限制，車輛自身狀態的約束也是重要的舉措，盡可能地減少作業場景的動態信息是保證生產穩定的一個前提。

1.2 場景建模

將實際作業空間轉換為模型地圖是算法研究的第一步。目前常見的地圖構建方法有柵格圖法、可視圖法和拓撲圖法。拓撲結構簡潔直觀，對地圖進行全局規劃的效率高。柵格地圖精細化程度高，適合車端進行局部路徑規劃。為充分發揮二者的優勢，本文在云端使用拓撲地圖進行全局規劃，并結合車端柵格地圖進行局部規劃，最大限度保證路徑規劃的準確性和穩定性。

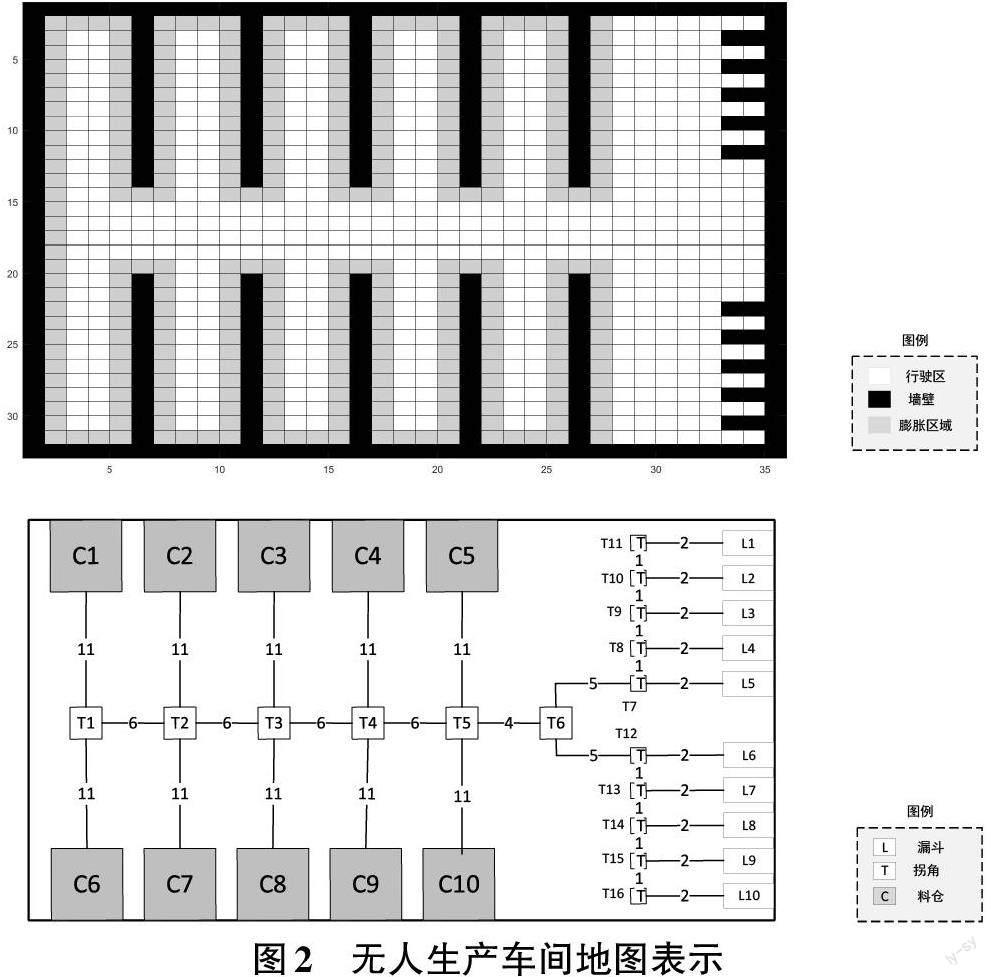
柵格圖法將實際三維地圖二維化，使用整齊排列的柵格來代表地圖中的路徑和障礙物。其中1代表障礙物，不可通行由圖2上中黑色柵格表示；0代表路徑，可通行由圖2上中白色柵格表示[11]。柵格圖表示法在場景開闊或細小障礙物較多的場景時，由于自身精細化表達能力差，刻意縮小柵格大小又會極大地增加計算量。故而并不適用于繁雜的作業場景。考慮到無人裝載機裝卸料生產車間場景固定，作業范圍比較小，同時嚴格控制生產區間障礙物等動態事件。使用柵格地圖足夠達到任務的精度，也有利于管理控制。無人生產區間使用柵格地圖表示后的場景如圖2 所示。為了提高作業的安全性，在柵格地圖中設立了膨脹區域由圖2上中灰色柵格表示，膨脹區域內的行進代價會增加，以降低路徑規劃撞墻的概率。

2 路徑規劃算法

路徑規劃算法的任務是從當下環境中尋找出一條無沖突，從起始點到終點路徑代價最小的路徑。基于1.1所描述的場景可以將路徑的沖突分為頂點沖突和邊界沖突。

2.1 沖突概述

2.2 CBS 算法

CBS算法是由Guni等人于2015年提出的用于解決多目標路徑規劃MAPF （Multi-Agent PathFinding，MAPF） 路徑沖突問題的方法。CBS算法的主要思想是通過尋找一系列連續的約束來處理所有目標路徑的沖突，直到找到沒有沖突點的路徑集合。CBS是一個雙級（two-level） 搜索算法，高級搜索部分（highlevel）是一個二叉搜索樹，稱為沖突樹CT（ConflictTree） ，樹的每個節點包含了單條的路徑的基本信息和約束條件。算法低級部分是在考慮新增約束的情況下，使用A*算法重新計算得到的最短路徑。

CBS算法在目標數量過多，或者路徑沖突密集的情況下，搜索到的路徑可能陷入局部最優解，但是對于目標數較少的模型（如雙目標模型）中卻有著足夠高的效率和性能。在本文的雙裝載機作業場景中，使用CBS算法是高效的。

2.2.1 CBS 高級搜索

CBS高級搜索由沖突樹完成，樹的每一個節點N包含了三個部分：

1） 一系列的約束（N.constrains） 。每一個約束都作用于某一路徑，根節點的約束為空，子節點繼承父節點的約束。

2） 局部最優路徑（N.solution） 。目前的節點路徑，路徑需要滿足所有約束。該路徑計算由A?算法完成。

3） 總代價（N.cost） 到該節點為止，得到的所有路徑總代價。

具體結構及沖突處理如圖5所示。

首先，規定沖突樹的左子樹給節點1添加約束，Con 為節點約束，Cost 為路徑代價，sol 為目前的路徑集合，標紅部分為沖突點。該二叉樹有如下特點：

1） 根結點約束為空；

2） 子結點繼承父節點的所有約束，并且所有路徑都是在以約束為前提的情況下得到，通過低級搜索得到；

3） 一旦搜索到目標結點，該遍歷即可提前結束。

總體上，需要先使用A? 算法進行低級搜索為所有的目標ai 尋找最短路徑（N₁.solution），并且該低級搜索繼承了所有來自父節點的約束（N₁.constrains）。一旦找到新的連續路徑，需要重新計算這些路徑的總代價（N₁.cost），并且這些目標點的新路徑會重新進行沖突檢測。若沖突依然存在，則在該節點的基礎上增加新的約束。兩個新的約束分別作用于沖突的兩個目標點，生成兩個新的子節點N₂，N₃繼承于N₁。依次遍歷直到為所有的目標尋找到無沖突的路徑。

初始給定兩條沖突的最短路徑1：{ D2，C2，B2，A2，A3}2：{C1，B1，B2，B3，B4}。t = 2 時，兩條路徑在B2點發生頂點沖突。左子樹為路徑1添加約束Con：{1，B2，2}，路徑1在t = 2時不得通過B2點，新路徑為1：{ D2，D3，C3，B3，A3}2：{C1，B1，B2，B3，B4}。重新計算新路徑的沖突，并以相同的方式解決，最終得到兩條無沖突的局部最優路徑：

類似地，沖突樹的右子樹為路徑2添加類似約束，重新計算得到新的路徑集合。一般地，最終沖突樹得到的多個局部最優解需要通過路徑代價Cost 做進一步篩選，但若僅以距離代價為代價總和，則沖突樹深度越深的節點代價會越高，故而一旦搜索到無沖突路徑即可解決CBS搜索。

對于多個目標（> 2） 的路徑規劃，可以生成k 個子節點構成約束森林，如圖6（a） 所示，節點1，2，3在t 時刻在v 處都發生了沖突。優先考慮節點1，2的沖突，處理之后再考慮加入節點3的沖突，從而將森林拆分為二叉樹進行新的迭代，如圖6（b） 所示。

綜合以上，CBS算法高級搜索的算法流程由表1 給出。

3 仿真實驗分析

為了驗證CBS路徑規劃算法在裝載機裝卸料模型中的有效性，本文通過OpenCV工具庫對算法進行驗證分析。柵格地圖用于裝載機車端的局部路徑規劃，拓撲圖用于云端全局路徑規劃，由此可以清晰地表示出CBS算法尋找出的路徑并實現精細化控制。

3.1 路徑規劃沖突仿真分析

針對兩種不同類型的沖突，設置一系列不同的任務以充分證明算法的有效性。任務序列如表2所示。

每一個裝料任務都包括了兩段距離，分別為裝載機起始位置St 到料倉C 和料倉C 到漏斗L。并且起始位置到料倉階段，裝載機空載，此時行駛的代價較小。

相反的，料倉到漏斗的距離階段，裝載機滿載，此時設定裝載機的行駛代價為空載時候的2倍。

假設兩輛裝載機的起始點分別為L1和L10，并且為方便計算，裝載機到達任務地點后的作業時間代價固定為11。首先由A? 算法根據任務列表尋得的最短路徑如表3所示，表中所有的路徑都使用圖1拓撲圖結構來表示。為解決路徑沖突，同時使得路徑的代價最小，約定空載裝載機需要為滿載運行的機械讓步，由此使用CBS算法得到新的無沖突路徑并計算其代價如表4所示。

綜上實驗結果，雙車模型在固定的裝卸料作業場景中沖突次數較少，在本文選取4個任務單次CBS計算中僅有3次沖突。同時運行過程中只要保證滿載車輛運行的路徑最短，則相應的任務總代價就會越小。由此證明了CBS算法在該應用場景中不僅高效簡單，更有不錯的穩定性。

4結論

本文針對無人裝載機裝卸料作業場景進行路徑規劃分析，提出一種符合實際生產需求的解決方案，并通過實驗分析證明了在固定的作業場景中，CBS算法在路徑規劃中的高效性。除此之外，采用柵格地圖進行路徑規劃的局部規劃，便于精確地控制車輛運行狀態；拓撲地圖進行路徑規劃的全局規劃，方便操作人員及時地調整，增強了算法的實用性。

實驗證明了在局限的場景中，CBS 算法簡單高效，且具有不錯的穩定性。在保證裝載機滿載運行路徑最短的情況下，可以得到規劃路徑的最優解。如何更精細化地考慮機械運行的其他參數，提高整個路徑規劃算法的魯棒性是后續工作需要研究的內容。