基于動態軋制力的四輥軋機垂直震動及扭轉震動特性探析

肖志明

（福建省三鋼冶金建設公司，福建 三明 365000）

隨著我國工業化進程的逐漸提升，軋機已經是各工廠中所必不可少的生產設備，但是在日常生產過程中，軋機振動問題一直為工作人員所困擾，一定程度上影響了企業產品質量的提升。而在如今軋機垂扭耦合系統非線性振動機理的研究還不是很完善，難以得到有效利用。所以，為了改變這一現狀，對四輥軋機垂直震動及扭轉震動特性的研究是十分必要的。本文在考慮動態軋制力的基礎上，建立四輥軋機垂直—扭轉耦合振動動力學模型，結合實際軋機工作參數對其性質進行研究。

1 動態軋制力和動態軋制力矩模型

在忽略潤滑因素的影響下，依照軋制生產中軋制帶材的受力情況，將軋制變形過程簡化為如圖1 所示的力矩模型。

圖1 中各項標注分別為：穩態軋制時，軋件入口厚度H；穩態軋制時，軋件出口厚度h；軋輥半徑R；軋件所受前張力τf；軋件所受后張力τb；上輥垂直方向振動位移x1；下輥垂直方向振動位移x2；輥旋轉速度v0；軋件咬入角度α。

計算公式：

其中，K 為主應力影響系數， 通常情況下K=1.15σ，σ 是材料變形阻力；KT是張力影響系數；Qp是外摩擦影響系數；Le是軋輥和軋件接觸弧的水平長度；B 是軋件寬度。

通過以下模型完成對材料變形阻力的計算。

將各式全部帶入F=BleQpKTK 后進行泰勒展開，可得動態軋制力為：

其中，ΔF 代表軋制力動態變化量；F1代表穩態軋制力。

2 四輥軋機垂直-扭轉耦合振動動力學模型

考慮到動態軋制力和動態軋制力矩的影響，建立四輥軋機垂直—扭轉耦合振動動力學模型見下圖2 所示。

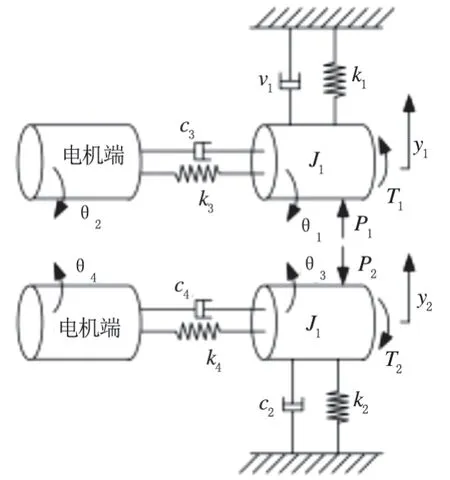
圖2 四輥軋機垂直-扭轉耦合振動動力學模型

圖2 中各項標注分別為：

上輥旋轉角度θ10；下輥旋轉角度θ20；上下傳動系統電機端旋轉角分別為θ30、θ40；上下輥系上動態軋制力矩為T1、T2；上下輥系所受等效合力為P1、P2；上輥系與上橫梁間的等效阻尼c1；下輥系與下橫梁間的等效阻尼c2；上下輥系與電機端間的等效阻尼為c3、c4；上輥系與上橫梁間的等效剛度k1；下輥系與下橫梁間的等效剛度k2；上下輥系與電機端間的等效剛度為k3、k4；上下輥系等效轉動慣量為J1、J2；上下輥系的等效質量為m1、m2。

由此可以得到四輥軋機垂直—扭轉耦合振動方程為：

在工作輥質量遠小于支撐輥時，因為軋機結構與振動的對稱性，存在m1=m2，k1=k2，c1=c2，y1=y2，x1=x2，p1=p2，J1=J2，k3=k4，c3=c4，θ1=θ2，θ3=θ4，T1=T2。

令y=x1可得：

3 四輥軋機耦合振動方程主共振響應求解

設軋機在軋制過程中，受到周期性的外部擾動

設其解為：

代入后令，消除久期項得：

4 仿真分析

圖3 和圖4 為變化參數條件下的幅頻曲線。

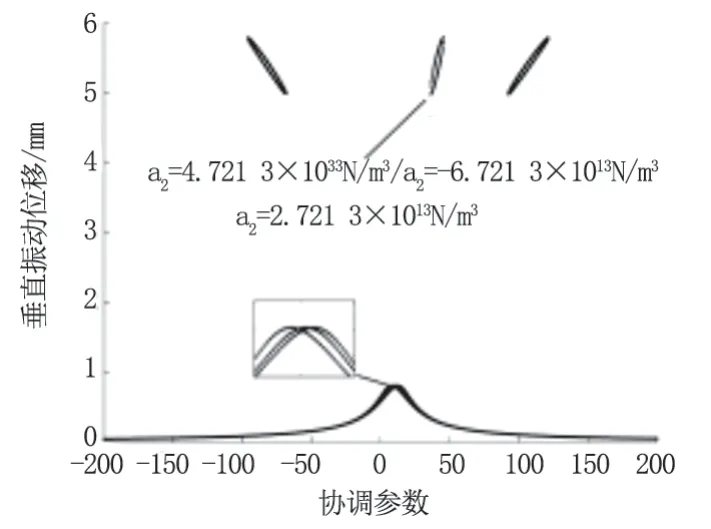
圖3 a2 變化下豎直方向共振幅頻

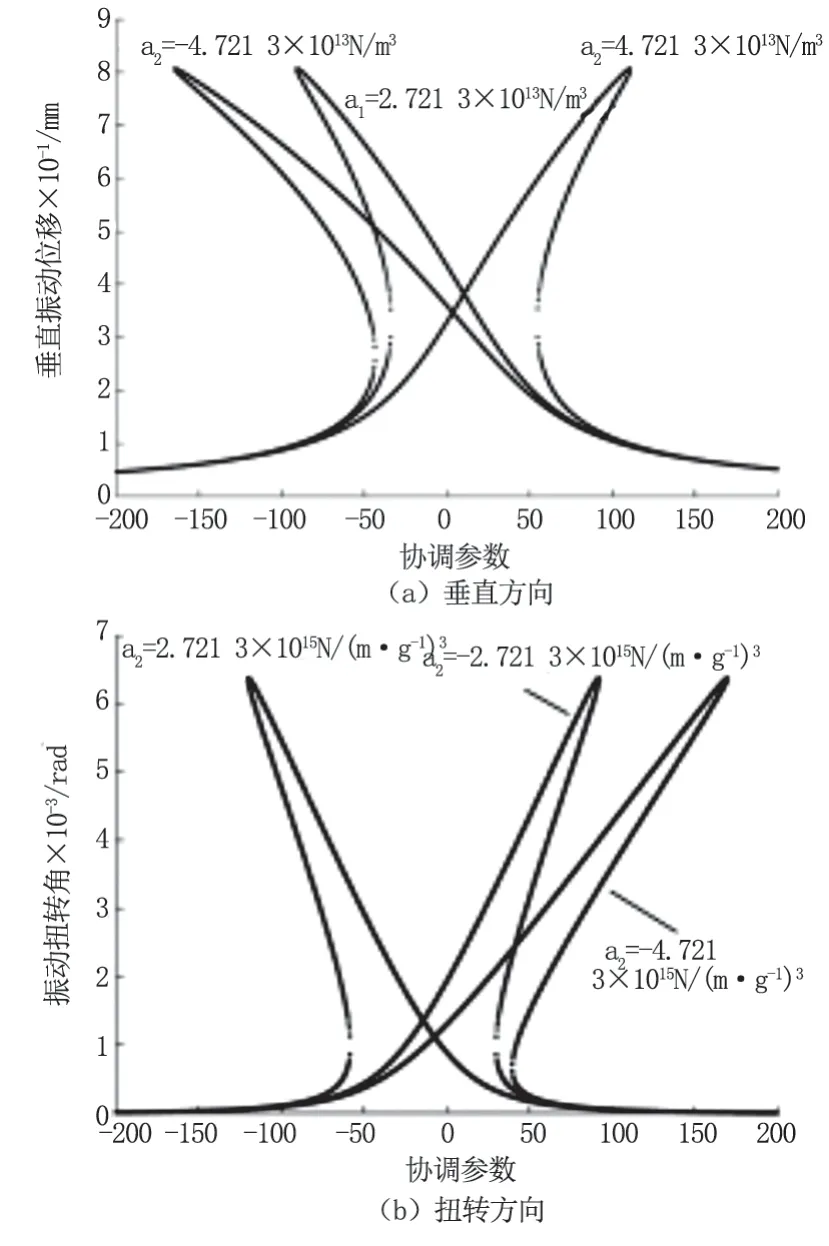
圖4 a2 變化時垂直和扭轉方向主共振幅頻曲線

圖3 是指在系數a2 發生變動的情況下，軋機幅度頻率曲線有“跳躍圈”現象發生，在這時在跳躍圈范圍里軋機會發生非常明顯的主共振現象。

圖4 為參數a2 在較大值變化下，軋機垂直和扭轉方向幅頻特性曲線。從圖中我們能夠得到的信息是a2的變動不僅能夠使軋輥在垂直方向發生跳躍，也能夠使軋輥在扭轉方向發生跳躍現象。

圖5 中為外擾力幅值F0 變化下軋機在垂直和扭轉方向的全局分岔曲線。可以看出，軋機在垂直和扭轉方向都出現了多種運動形態。

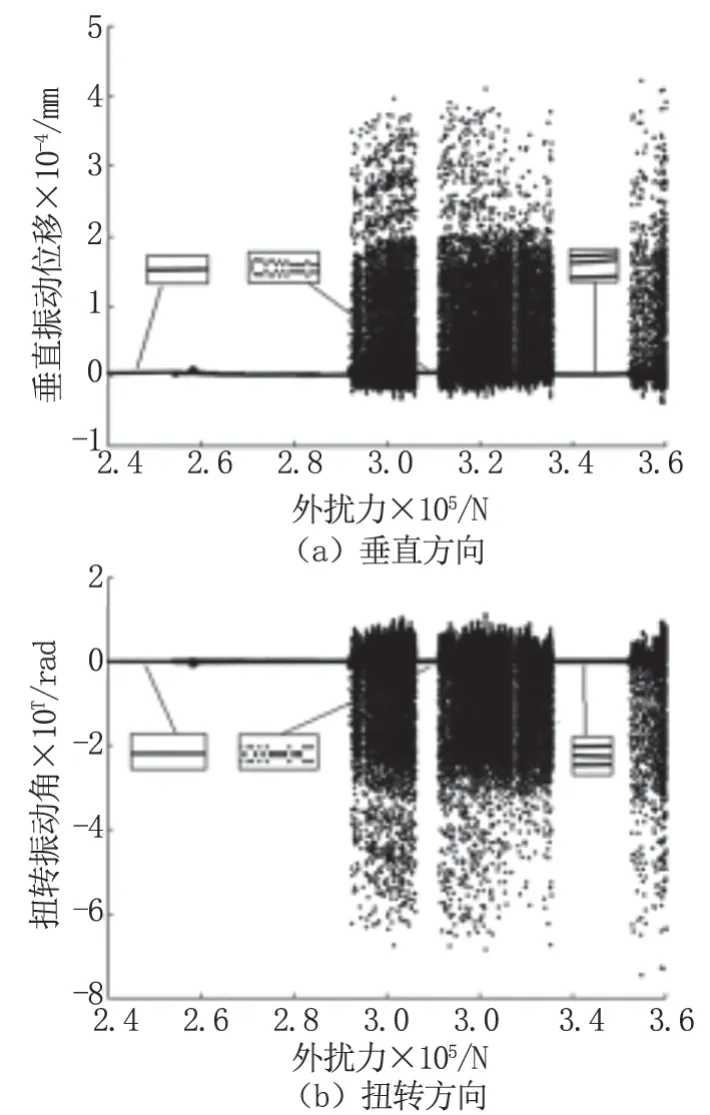
圖5 外擾力F0 變化下軋機的局部分岔圖

5 結語

本文采用多尺度法，利用四輥軋機垂直—扭轉耦合振動動力學模型，再結合實際軋機工作參數，研究在不同參數變化情況下的四輥軋機垂直震動及扭轉震動呈現出的不同狀態，例如，外擾力化時軋機主共振幅頻，F0 值為2.495×105N、3.081×106N、3.235×105N 時軋機的狀態。以期能夠為研究解決軋機震動問題提供參考。