水下儲氣裝置的水動力學特性分析*

劉超群,謝迎春,李相坤,白 亮

(中國海洋大學 工程學院,山東 青島 266100)

0 引 言

截至2022年6月底,我國火電發電量占總發電量的68.24%。作為主要的發電方式之一,火力發電引發了大量的碳排放。大量的碳排放造成了全球變暖和氣候變化等危害[1,2]。在此背景下,開發新能源發電成為必然趨勢。然而,可再生能源存在著明顯的間歇性、隨機性等問題,因此,需要儲能系統來解決這一問題[3]。

因其調節速率快、容量配置靈活等特點,儲能系統受到了業界人士廣泛的關注[4]。作為儲能技術的一種,水下壓縮空氣儲能十分適用于海上大規模新能源發電系統[5-7]。水下儲氣裝置作為水下壓縮空氣儲能系統中的關鍵部件,一方面要承受巨大的空氣壓力,另一方面還要承受復雜多變的環境載荷,這就要求水下儲氣裝置擁有更高的結構強度。

水下儲氣裝置一旦發生損壞,整個儲能系統及周圍設施與環境將會遭受嚴重損害[8,9]。因此,筆者選取水下儲氣裝置作為研究對象,對水下儲氣裝置在海流環境下的水動力特性進行研究,為水下儲氣裝置的結構強度設計與水動力學分析提供參考。

對于水下儲氣裝置的流體動力學研究,國內外學者大多采用數值模擬的方法。

孫川等人[10]采用計算流體動力學(computational fluid dynamics,CFD)方法,分析了負壓吸附裝置的流場特性;但其未對負壓吸附裝置進行受力分析。王金舜等人[11]采用了大渦模擬方法,對不同海流條件下的水下儲氣裝置流體動力學特性進行了數值模擬;但其未通過實驗對數值模擬結果進行驗證。WANG Z W等人[12]采用大渦模擬方法,分析了全尺寸水下儲能裝置時均和瞬態流動結構及其受力特性。VASEL-BE-HAGH A R等人[13-15]分別采用k-ω和LES Dyna-SM兩種湍流模型,對氣球狀儲氣裝置周圍的流場結構及受力特性進行了分析,結果發現,儲氣裝置后部可能產生旋渦形式與旋渦脫落過程,并得到了儲氣裝置升阻力系數與渦脫頻率;但該研究集中于數值模擬,沒有對數值模擬結果進行對比驗證。WANG Z W等人[16,17]使用標準的k-ω模型,研究了不同雷諾數條件下氣球狀儲氣裝置的受力特性及流場結構,結果發現了k-ω模型能夠預測時均水動力特性;但k-ω模型不能捕捉到瞬態的湍流特性,且其對于力系數的計算結果偏大。

綜上所述,國內外許多學者對水下儲氣裝置進行了流體動力學研究,但大多數研究是采用數值模擬的方法進行的,而很少有研究者采用數值模擬與模型實驗相結合的方法。

筆者將已有的氣球狀儲氣裝置作為研究對象,采用結合數值模擬與模型實驗的方法,對氣球狀儲氣裝置的受力特性及流場結構進行分析,探究氣球狀水下儲氣裝置的水動力學特性。

1 理論分析

1.1 物理參數定義

為了描述水動力系數的變化規律,筆者引進了無量綱雷諾數Re,其計算公式如下:

(1)

其中:

(2)

式中:ρ為海水密度,kg/m3;U為自由流速,m/s;μ為海水的動力黏度,Pa·s;D為特征長度,m;V為鈍體體積,m3。

筆者選擇黃海海域作為研究環境。經過調研得知,海水密度為1.025×103kg/m3,平均流速范圍為0.1 m/s～0.25 m/s,該海域的平均溫度為16.5 ℃,該溫度下海水的動態黏度為1.001 4×10-3Pa·s[18]。

根據莫里森方程,升力系數(CL)與阻力系數(CD)由下式進行推導,即:

(3)

(4)

式中:FL,FD為儲氣裝置所受的升力、阻力,N;SL,SD為儲氣裝置在升力、阻力方向上的投影面積,m3。

1.2 LES湍流模型

筆者在對圓柱鈍體繞流進行數值模擬時發現,相比雷諾時均法模型,利用LES湍流模型仿真得到的結果更加穩定和精確。并且,自由端效應能夠更加容易地被觀測到。

筆者將進行過良好檢測的Smagorinsky-Lilly LES模型應用于不可壓縮流動的Navier-Stokes方程。

經過濾波處理后的方程如下:

(5)

(6)

式中:u為速度,m/s;p為壓力,N;ρ為密度,kg/m3;τij為Smagorinsky-Lilly模型中的次網格尺度應力,N。

次網格尺度應力計算公式如下:

(7)

(8)

(9)

(10)

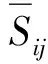
2 水下儲氣裝置水動力實驗

2.1 實驗模型設計

筆者選取SUBSALVE USA CORPORATION公司生產的專業(PF)系列水下升力氣球作為研究對象[19]。

根據水動力實驗室的實驗條件以及模型材料強度,筆者按照相似準則對模型進行縮放,選定縮尺比為1∶10,從而得到了該次實驗的實驗模型。

實驗模型設計圖如圖1所示。

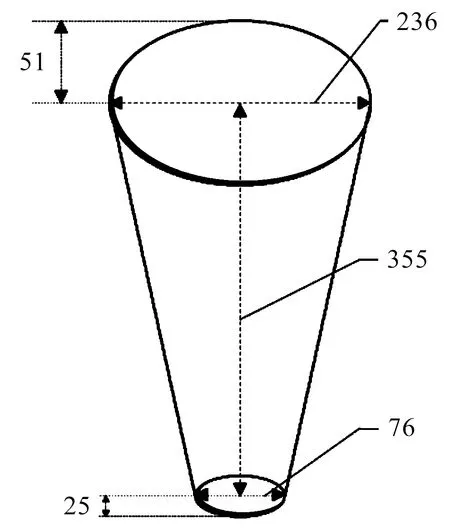
圖1 實驗模型設計圖

在實驗模型時,筆者首先利用連接桿將模型與六維力傳感器連接起來,然后使用G型夾,將六維力傳感器固定在水槽測試段的工裝架上。

儲氣裝置實驗模型圖如圖2所示。

圖2 儲氣裝置實驗模型圖

2.2 實驗測試平臺及實驗參數

實驗在中國海洋大學海洋工程重點實驗室的隨機波流耦合水槽中進行。該水槽長60 m,寬3 m,深1.5 m,水槽一側配有造流系統自動控制軟件。

實驗過程中,筆者設置水深為1.12 m,實驗模型放置于水槽中部,從而保證了穩定流速所需的距離。

實驗水槽圖如圖3所示。

圖3 實驗水槽圖

為保證實驗模型與實際模型的雷諾數相似,實驗工況的流速計算公式如下:

(11)

(12)

式中:D為儲氣裝置特征直徑,m;Dm為儲氣裝置模型特征直徑,m;ρ為海水密度,kg/m3;μ為海水的動力黏度,Pa·s;V為海流速度,m/s。

具體實驗參數表如表1所示。

表1 實驗參數

為保證實驗數據的準確性,筆者搭建了包括六維力傳感器、振動加速度傳感器及流速傳感器在內的多傳感器融合采集系統。

儲氣裝置模型實驗的測試系統如圖4所示。

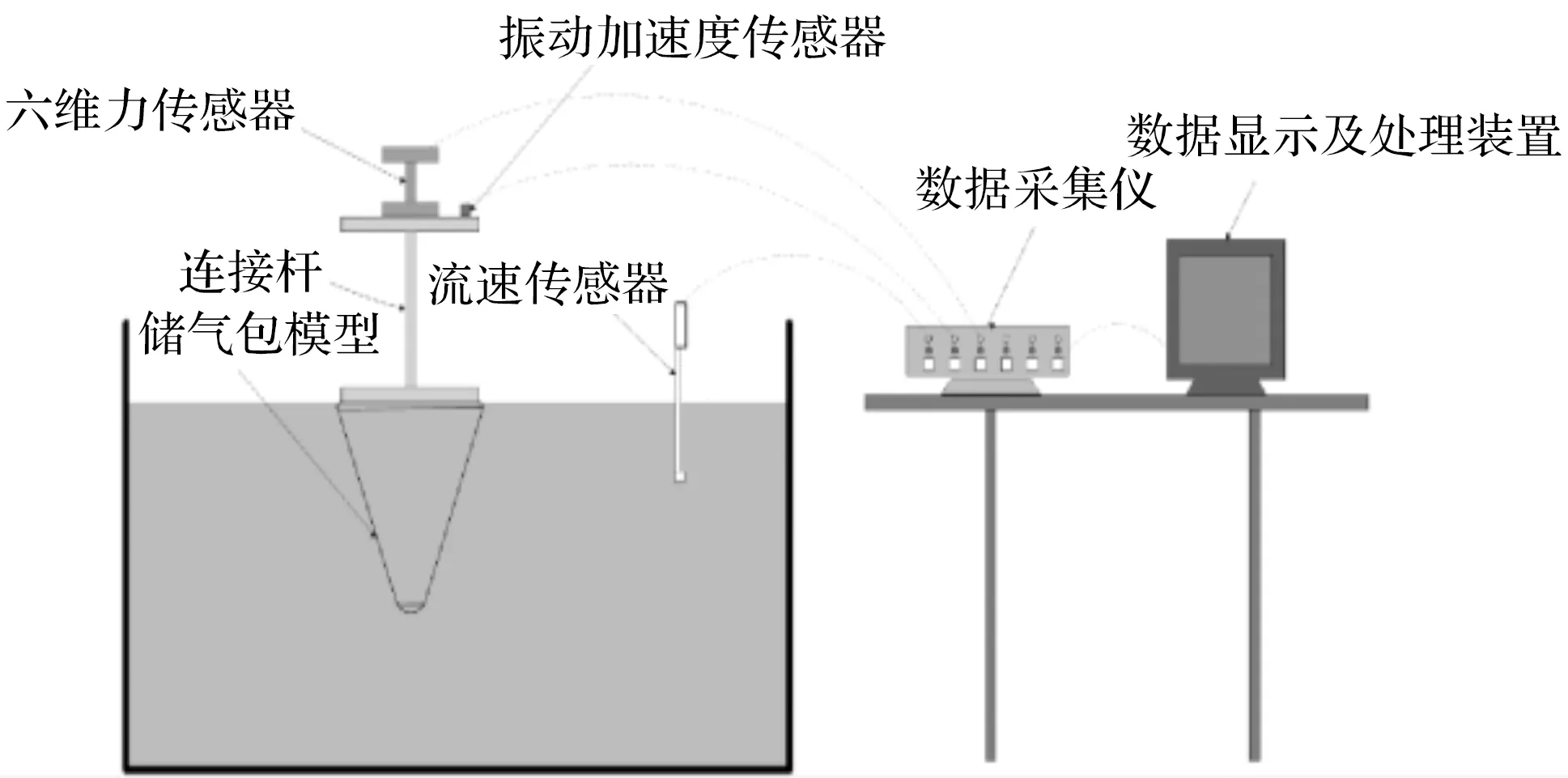
圖4 儲氣裝置模型實驗測試系統

實驗測試系統中,六維力傳感器的最大阻力測量量程為±500 N,靈敏度為1 mV/V。所有數據由八通道的無線動態應變采集儀(DH5902)集中采集處理,采集儀的采集頻率為10 kHz。流速傳感器用于采集實驗過程中的實時流速信號。振動加速度傳感器用于實時監測模型的振動加速度信號。

為了避免實驗數據的偶然性,筆者每組實驗重復測試,并取平均值作為實驗值。

2.3 實驗數據處理

不同流速下,水下儲氣裝置力系數結果圖如圖5所示。

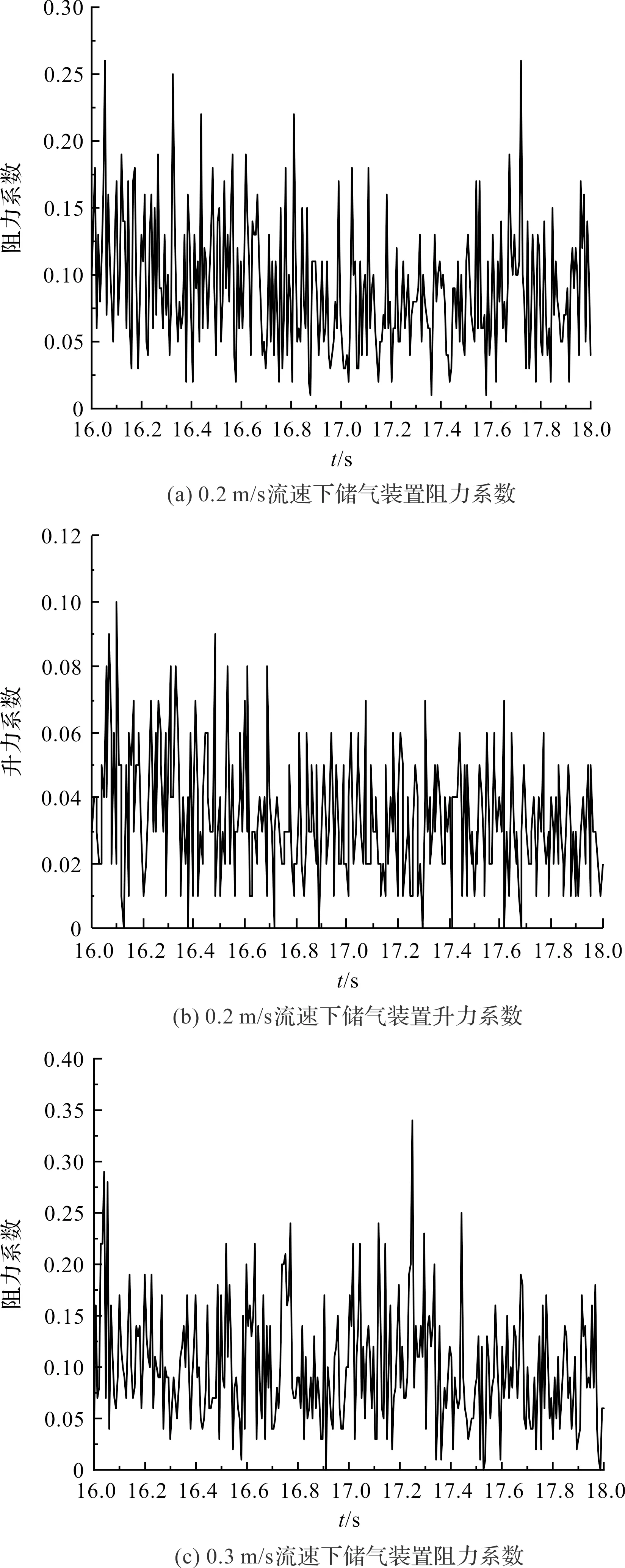
圖5 不同流速下水下儲氣裝置力系數結果圖

由圖5得:儲氣裝置發生渦脫落時,阻力系數與升力系數會在一定的穩定值范圍內波動。隨著工況流速的增大,儲氣裝置脈動頻率也隨之增大。

不同流速力系數平均值如表2所示。

表2 不同流速力系數平均值

由表2可得:隨著流速的增大,儲氣裝置承受的阻力和升力逐漸增大。由于渦街的存在,儲氣裝置在橫流方向上承受的流體力隨時間周期性地變化。當流速為0.4 m/s時,儲氣裝置升力系數的波動表明其側向存在一對交替產生的旋渦。

3 數值模擬

3.1 數值模型建立

為減少數值模擬的計算量,筆者忽略掉了儲氣裝置的設計細節,將儲氣裝置簡化為氣球狀物理模型,創建了與實驗模型尺寸相同的三維數值模型。

簡化后儲氣裝置三維模型圖如圖6所示。

圖6 簡化后儲氣裝置三維模型圖

在進行網格劃分時,為保證計算精度,筆者將計算域劃分為18塊,并在包含儲氣裝置模型的區域中采用非結構化網格,其余區域均采用結構化網格。

同時,為了對儲氣裝置的受力狀況進行準確監測,筆者對儲氣裝置壁面進行了邊界層網格劃分,隨后進行網格獨立性檢驗。

網格無關性結果如圖7所示。

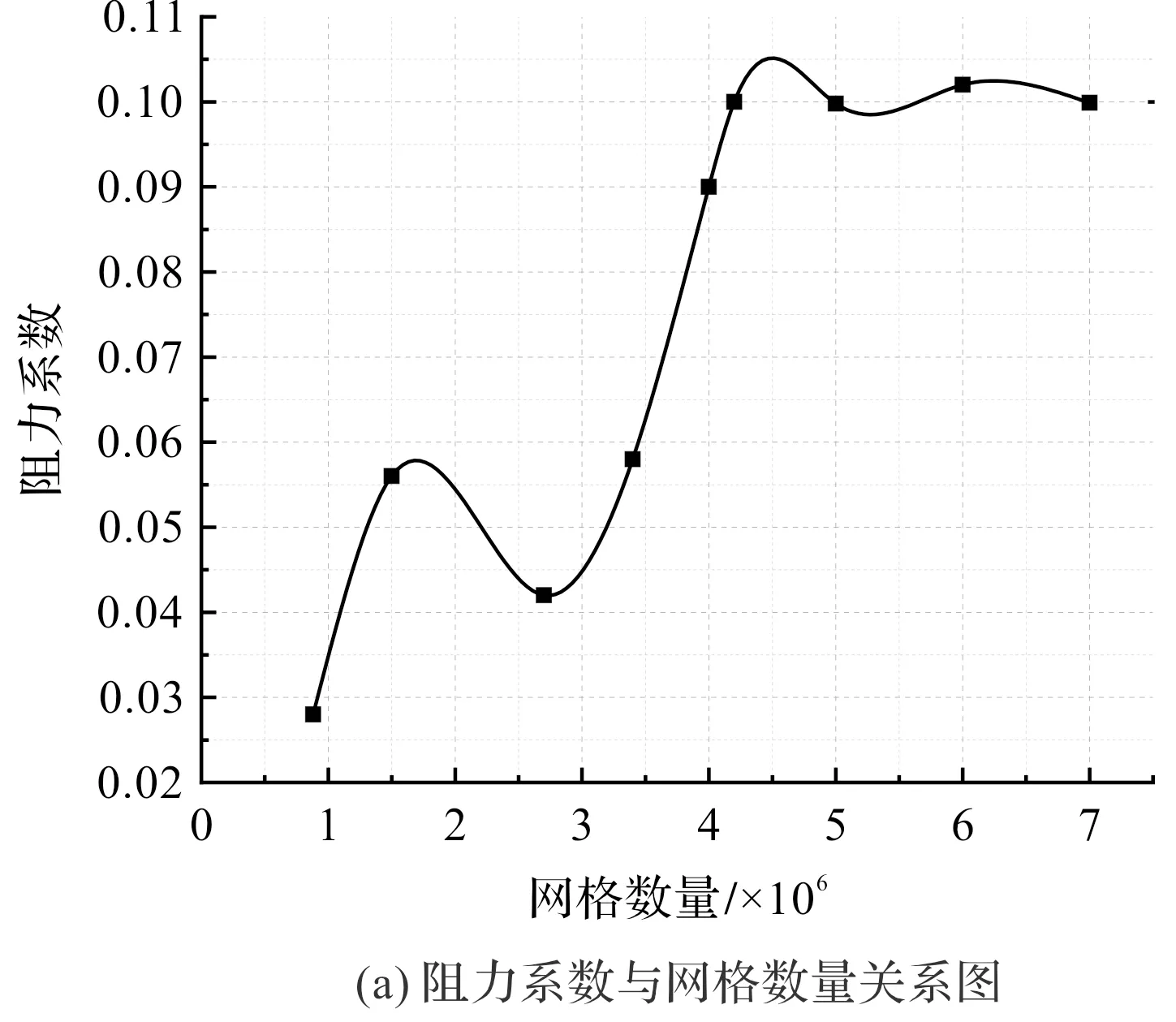
圖7 網格無關性結果

由圖7可得:在網格數量達到4.1×106個時,儲氣裝置的力系數幾乎不再隨網格數量變化而變化。

在數值計算過程中,離散格式對求解結果有著重要影響。BREUER W等人[20,21]對此進行了研究,發現了低階迎風格式無法用于準確捕捉回流區長度。因此,筆者在對儲氣裝置進行數值模擬時,選取高階迎風格式進行了計算。在進行求解設置時,筆者選用Smag-orinsky-Lilly模型,對亞格子湍流黏度系數進行了求解(Smagorinsky參數設置為0.1)。

為避免在計算過程中因浮點溢出而導致計算中斷,筆者在進行數值模擬時對時間步長進行設定。時間步長計算公式如下:

(13)

式中:Δt為時間步長;Vd為X、Y、Z這3個方向上的對應速度,m/s;Δd為3個方向上的對應網格最小尺寸。

3.2 模擬結果分析

3.2.1 流體力分析

筆者將0.4 m/s流速下儲氣裝置的數值模擬結果與實驗結果進行比較,得到儲氣裝置力系數時間歷程圖,如圖8所示。

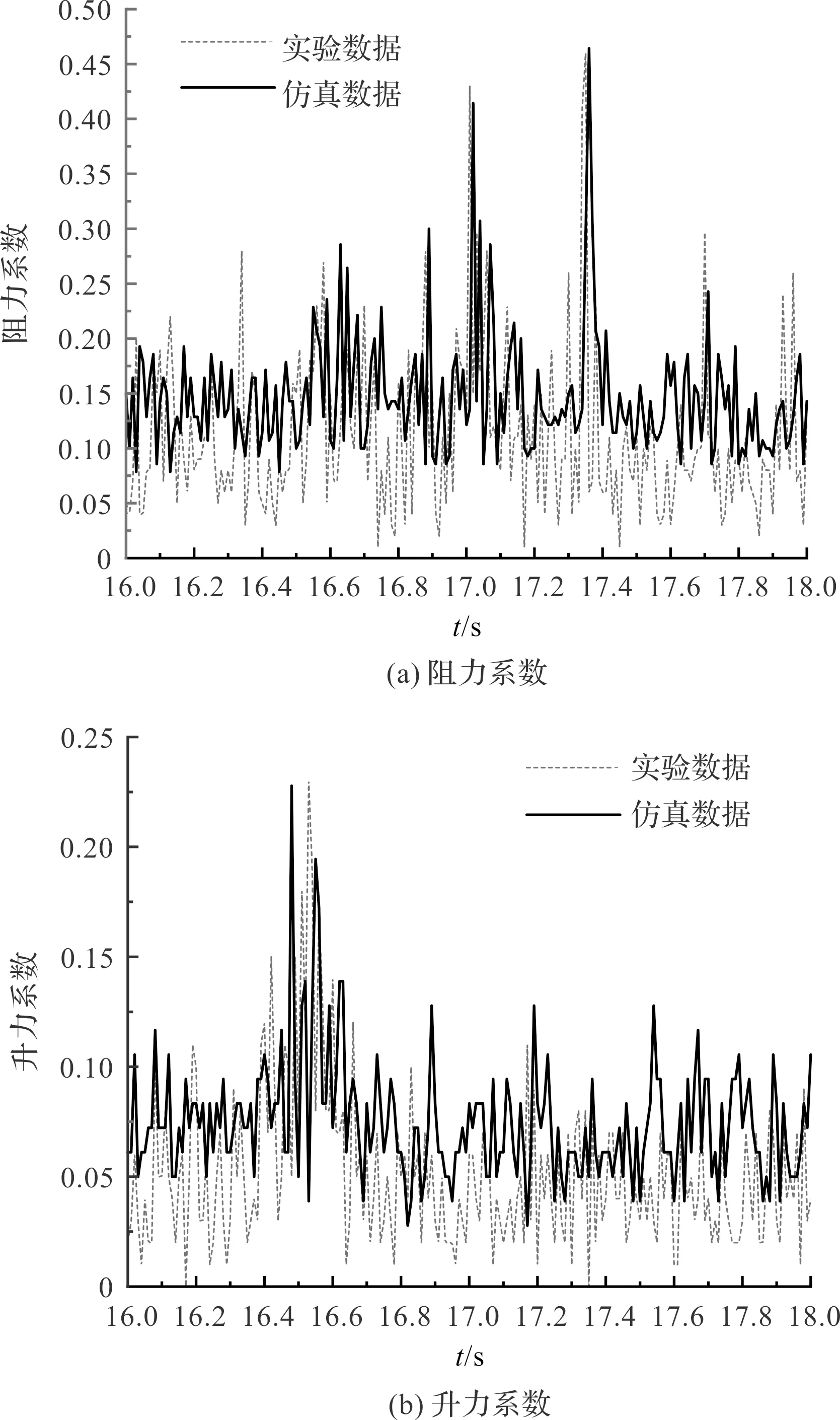
圖8 儲氣裝置力系數時間歷程圖

由圖8可得:采用LES湍流模型進行計算時,仿真所得的瞬態結果收斂,且呈現出寬帶湍流特征,模型阻力系數和升力系數均趨于平穩;

同時,實驗結果略大于仿真結果,其主要原因是實驗模型表面存在一定粗糙度,但在數值模擬中模型表面被處理為光滑表面。表面粗糙度增加了實驗模型的摩擦阻力,從而導致實驗測得的結果較大。

0.4 m/s流速下,實驗與仿真力系數平均值如表3所示。

表3 實驗與仿真力系數平均值

由表3可得:模型平均升力系數不為零,這是由模型非對稱結構導致的。模型下表面的壓力大于上表面的壓力,因此產生向上的升力。由于模型迎風面的壓力比背風面的壓力大,因此會產生向后的壓阻。

由于實驗與仿真所得的模型力系數非常接近,因此,筆者采用LES湍流模型進行數值模擬時,其計算結果是可以接受的[22]。

3.2.2 尾跡流場分析

在流體力學中,渦量是描述旋渦運動的常用物理量[23]。在渦量的計算中,來自流體形變而導致的旋度變化通常會被計算在內,但實際上流體并未發生旋轉運動。

所以HUNT J等人[24]提出了Q-criterion,其定義如下:

(14)

式中:Ω為渦量張量;S為變形張量。

根據Q-criterion準則,氣球狀水下儲氣裝置的瞬時流場渦結構圖,如圖9所示。

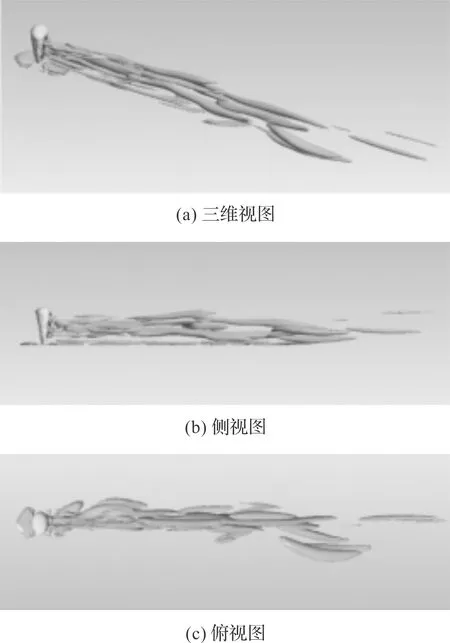
圖9 氣球狀水下儲氣裝置的瞬時流場渦結構

由圖9可得:采用LES湍流模型進行數值模擬時,氣球狀水下儲氣裝置的瞬時流場渦結構和尺度比較復雜,并且流場中存在明顯扭曲的卡門渦街;繞流形成的旋渦具有明顯的三維結構特征,流經儲氣裝置側向的流體在裝置背風面附近逐漸扭曲形成旋渦結構;背風面附近區域兩側的旋渦關于流場中面對稱分布,并經過裝置頂部后形成分離渦,從而導致海水向下運動;分離渦在裝置半高處附近與側向向下扭曲的旋渦合流,形成下行海流。下行海流的出現是尾跡流場中豎直方向負速度流體出現的原因之一。

0.4 m/s流速下,流場內的流場流線圖如圖10所示。

圖10 流場流線圖

由圖10可得:儲氣裝置背風面出現流動分離現象,并伴有旋渦。由于流動的不穩定性,當流體從儲氣裝置流過時,儲氣裝置后部會發生旋渦脫落現象。儲氣裝置表面產生脈動的壓力分布,從而使其受到脈動的流體力,導致儲氣裝置出現渦激振動現象。當渦激振動頻率與儲氣裝置固有頻率接近時,儲氣裝置會發生鎖頻共振現象,從而受到嚴重的疲勞損傷。

在0.4 m/s流速下,對稱面速度矢量圖如圖11所示。

圖11 對稱面速度矢量圖

由圖11可得:在儲氣裝置工作過程中,由于受到渦流的影響,周圍流體的速度響應會增加。但儲氣裝置在水下工作區域的流速非常小,并且儲氣裝置配有壓載。所以,儲氣裝置不會對流場產生較大的擾動,也不會對海底環境造成破壞。

4 結束語

筆者采用數值模擬與模型實驗相結合的方法,對氣球狀水下儲氣裝置水動力學特性進行了研究,選擇LES湍流模型對氣球狀水下儲氣裝置進行了仿真分析,并利用實驗數據對數值模擬結果進行了驗證。

研究結果表明:

1)通過對比實驗結果可知,LES湍流模型模擬精度良好,對氣球狀水下儲氣裝置的流場形態及力系數的仿真結果較為準確;

2)在0.4 m/s流速下,氣球狀水下儲氣裝置的阻力系數與升力系數分別為0.09和0.04;

3)氣球狀水下儲氣裝置的頂部結構能夠抑制裝置頂部附近的回流現象,還可以有效地利用下洗流擾亂側向旋渦的規則形成與脫落。

筆者當前所得的研究結論對于水下壓縮空氣儲氣裝置的結構強度設計和水動力學分析具有重要的參考價值和借鑒意義。

未來,筆者將對儲氣裝置充放氣過程水動力學特性進行進一步研究。