一種基于屬性值權重的k-modes 聚類分析算法*

郝榮麗 胡立華

（太原科技大學計算機科學與技術學院 太原 030024）

1 引言

聚類分析是數據挖掘和機器學習等領域中的主要研究內容之一，它是將物理或抽象的數據對象根據某種相似準則劃分成多個對象類的過程，使得同一個類中的對象之間具有較高的相似性，而不同簇中的對象具有較高的相異性［1］，并已經廣泛地應用在基因分類［2］、股市波動的特征分析［3］、天光光譜特征分析［4］、文檔的分類［5］、圖像處理［6］等許多領域。聚類分析主要分為劃分聚類［7］、層次聚類［8］、密度聚類［9］和網格聚類［10］。k-means算法［11］是一種經典、常用的劃分聚類算法，具有簡單高效，易于理解和實現等優點，但在實際應用中，由于存在大量的分類型數據，k-means 方法不能處理包含分類屬性的數據集，限制了其實際應用領域。

k-modes［12］作為k-means 聚類分析算法的一種擴展，可適用于含有分類屬性的數據集，具有計算簡單、復雜度低等優點，但該聚類算法采用簡單匹配差異法，未能充分體現數據集的分布特征，將所有屬性視為同等地位，忽略了屬性之間的重要性差異，若頻率最高的屬性值有多個，傳統k-modes 算法無法選出最恰當的屬性值作為該簇模式。本文利用粗糙集中的等價類計算屬性值權重的思想，提出了一種k-modes 聚類分析算法。由于該算法充分利用了屬性值在數據集中的分布特征與屬性值自身的差異，有效地解決了屬性值之間的差異性度量，并利用屬性值頻率和各屬性值的權重，給出一種聚類中心更新途徑，從而有效地提高了聚類分析的效果。本文主要貢獻為

1）利用屬性值之間的差異和屬性值的權重，重新定義了相異度度量公式；

2）采用屬性值頻率和各屬性值的權重，給出了一種聚類中心更新迭代公式；

3）提出了一種基于屬性值權重的k-modes 聚類算法。

2 相關工作

k-modes 作為k-means 算法的一種擴展，根據分類數據的特點，采用簡單的0-1 匹配法來度量分類數據間的距離，用模式代替均值，但是這種采用簡單匹配差異法忽略了屬性之間的差異性，導致差異性度量不準確。對k-modes 改進的典型成果為：He［13］等使用屬性值在類內出現的頻率提出新的類內屬性距離計算公式；Hsu［14］等提出一種基于概念層次的方法來計算屬性值之間的距離，但該方法需要專家經驗；賈彬［15］等使用信息熵為屬性加權來解決屬性之間的差異問題，但是該方法在確定屬性權重時只考慮了某一屬性的分布，沒有考慮相關屬性對其的影響；白亮［16］等利用粗糙集中的上、下近似提出了一種新的相似性度量，改善了聚類效果，卻提高了計算的復雜度；趙亮［17］等基于樸素貝葉斯分類器中間運算結果計算屬性值之間的距離；黃苑華［18］等基于相互依存的冗余理論提出一種新的距離公式，采用內部距離和外部距離共同衡量兩個對象屬性值之間的距離，在進行外部距離計算時，僅從相關屬性的角度對屬性值在整個數據集上的分布情況進行描述，導致差異性度量不準確，這些算法不能夠準確應用屬性空間中數據間的關系，因而會丟失數據間的相似關系。針對傳統k-modes 算法中的模式問題，賈彬［15］提出了多屬性值modes 的相異度度量方法，每個屬性都保留全部屬性值和其出現頻率，但這樣也使得數據對象與modes 之間的距離計算變得復雜化。

綜上所述，k-modes 雖然將k-means 聚類分析算法應用范圍擴展到了分類數據集，但其多種距離度量都無法有效地度量分類數據之間的距離，未能充分體現分類變量間的差異，以及在整個數據集中的分布特征。

3 聚類目標函數與多屬性權重

為適用于分類數據的聚類分析，Huang 等于1998年提出了k-modes聚類算法，給定一組分類數據對象X={x1，x2，…，xn}和整數k（k≤n），數據集隨機初始劃分成k個互斥的簇，對數據對象迭代重定位簇，最終搜索得到使簇內平方誤差和，即目標函數F最小化的k個互斥的簇，參照文獻［12］，其目標函數定義如下：

聚類目標函數為

在式（1）中，W是一個n×k的{0 ，1} 矩陣，n表示數據集U中數據點的個數，k表示聚類的個數，Z={z1，z2，…，zk}，zl為第l 個類的中心點，zl={zl1，zl2，…，zlm} ，zlm是第l個類的第m個屬性上出現頻率最高的屬性值，d(xi，zl)為簡單的0-1匹配計算得出的分類變量間的距離。

多屬性值權重是屬性值在屬性空間中分布特征的體現，可從本地屬性和相關屬性兩個角度，來有效地刻畫屬性值在屬性空間上的分布特征。則參照文獻［19］，相關概念如下：

對于任意ai∈A，設xki∈Vai，從本地屬性ai的角度度量xki的單屬性權重為

從相關屬性aj的角度度量xki的多屬性權重為

結合本地屬性和相關屬性定義屬性值的權重為

其中：[xk]ai表示數據對象xk在屬性ai的等價類，表示屬性值xki和xkj的共現次數。屬性值權重W(xki)體現了屬性值在整個屬性空間中的分布特征。

4 基于屬性值權重的k-mode 聚類分析

兩個數據對象同一屬性下兩個值之間是否相似既取決于屬性值本身，又取決于其所處的環境，即屬性值所處的屬性空間［16］。可利用屬性值的權重來表示屬性空間的分布特征對屬性值相異度的影響，即外部相異度；同時，也需考慮屬性值本身之間的差異性，即內部相異度。因此，數據對象屬性值之間的相異度是由外部相異度和內部相異度共同決定，其相異度越大，距離也越大。

設xi和xj為數據集中的任意兩個數據對象，at為任一屬性，則參照文獻［18］，數據對象xi和數據對象xj在屬性at上的相異度度量公式重新定義如下：

在式（5）中，d1(xit，xjt)表示兩個數據對象屬性值本身的差異度，即內部相異度；d2(xit，xjt)表示兩個數據對象在整個屬性空間中分布的差異度，即外部相異度；1 2 表示兩種差異度的重要性相當，共同決定了屬性值之間的距離，差異度越高，距離越遠。

參照文獻［18］，數據對象xi和數據對象xj在屬性at上的內部相異度的度量公式如下：

在式（6）中，使用簡單0-1 匹配來計算兩個屬性值間的內部相異度。

由式（4）引入的屬性值權重，可得出第i個數據對象和第j個數據對象在屬性at上的外部相異度的度量公式如下：

式中W(xit)，W(xjt)分別代表屬性值xit和xjt對應的權重，用權重的差值來表示他們之間的外部相異度。

傳統的k-modes 算法在每個簇的每個屬性上選擇出現次數最多的屬性值作為該簇中心點在該屬性上的值，但是屬性上出現頻率高的屬性值有多個的話難以獲得最合適的中心點，因此，利用屬性取值的頻率以及屬性值的權重，重新描述類中心，并找出類中心對應的平均權重，從而可有效提高聚類精度。聚類族中心和對應的平均權重定義如下：

定義1 類l中某屬性at上某一屬性值的平均權重為該類中屬性at對應的該屬性值的所有權重之和的平均值。

定義2 類l的中心為zl={zl1，zl2，…，zlm} ，其中zlm為類l中數據對象在屬性am上出現頻率最高的，且具有最高平均權重的屬性值。每一個中心點對應一個平均權重集平均權重集代表模式中每個屬性值在屬性空間中的分布情況。

5 基于屬性值權重的k-mode 聚類算法

根據第3 節和第4 節的描述，在分類型數據集中，采用重新定義的相異度度量方式以及聚類簇中心選擇的聚類分析基本步驟為利用粗糙集中的等價類，計算數據集中所有數據對象的屬性值的屬性權重；隨機選擇數據集U中k個數據點作為初始的聚類中心；計算數據集中所有數據對象與k個聚類中心之間的相異度，然后將每個對象分配到與其相異度最小的聚類中心所在的簇中；在得到的k個簇中，更新簇的中心點及其對應的權重；重復上述兩個步驟，直到目標函數達到最小值，k個簇的類中心不再發生變化為止。算法偽代碼描述如下：

算法：MCAMAW（K-modes clustering algorithm based on multiple attribute weights）

輸入：分類數據集，簇的個數k

輸出：聚類簇

1）for（int i=0；i＜n；i++）｛

2）for（int j=0；j＜m；j++）｛

3） 利用xit在屬性at上的等價類，根據式（2）～（4）計算出屬性值xit的屬性權重W( )xit。

4）｝

5）｝

6）隨機初始找出k個簇中心，平均權重集為其對應的屬性值的權重

7）for（int i=0；i＜n；i++）｛

8） for（int cu=0；cu＜k；cu++）｛

9） for（int j=0；j＜m；j++）｛

10） 根據式（5）～（7）計算出所有數據對象與簇中心之間的距離，然后將各個數據對象

11） 分配到離其最近的簇中。

12）｝｝｝

13）for（int cu=0；cu＜k；cu++）｛

14） 根據定義1 和定義2 更新各個簇的中心及其平均權重集

15）｝

16）重復第7）步到第17）步，直至式（3）達到最小值，k個簇的類中心不再發生變化為止

17）返回聚類簇

6 實驗結果及分析

為了驗證所提MCAMAW 算法的有效性，從UCI數據集中選取Mushroom、Vote、Breast-cancer三個數據集，詳見表1 所示。采用python 語言實現了MCAMAW 算法、傳統k-modes 算法［12］和基于相互依存冗余度量k-modes 算法［18］，并分別從分類正確率、分類精度和召回率三個指標進行評價。

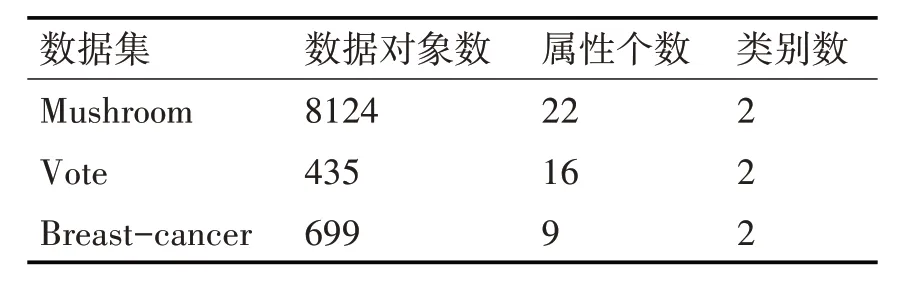
表1 UCI數據集

表2～4 給出了MCAMAW 算法與傳統k-modes算法［12］和基于相互依存冗余度量k-modes 算法［18］的實驗比較結果。可以看出在Mushroom、Vote、Breast-cancer數據集上MCAMAW 算法的三個指標均有所提高，聚類效果也優于其他兩個算法。其主要原因是MCAMAW 算法充分利用數據對象在數據集中的空間特征，準確地描述了數據對象之間的關系，有效地避免了其他兩個對比算法中分類數據對象之間距離度量不準確的問題。

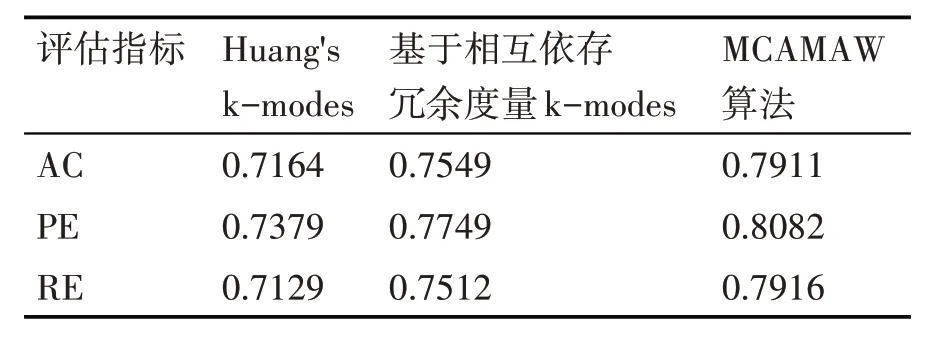
表2 Mushroom數據集

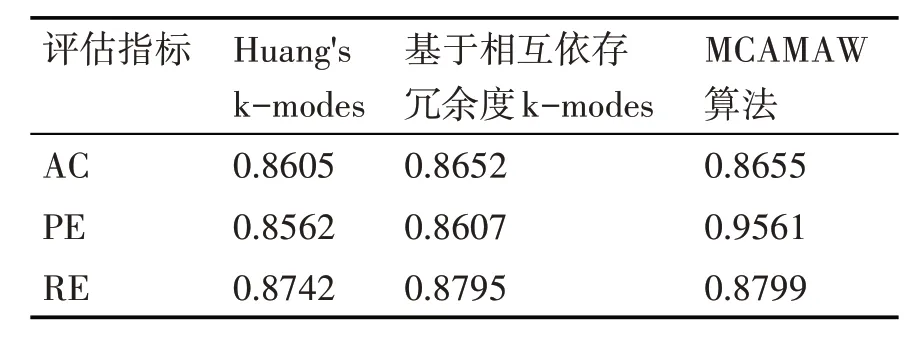
表3 Vote數據集

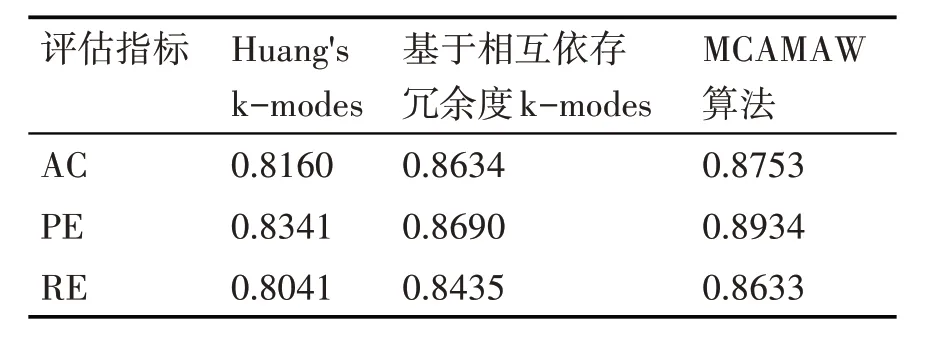
表4 Breast-cancer數據集

7 結語

本文采用多屬性權重，提出了一種k-modes 聚類算法。該算法從本地屬性和相關屬性兩個角度，描述了數據對象的屬性空間分布特征。在度量數據對象間的距離時，不僅考慮了數據對象本身的差異性，而且考慮了數據對象在整個屬性空間結構中的差異性。此外，在屬性值分布過于分散或相對均等時，可以根據屬性值的平均權重進一步確定模式中的屬性值，以便能夠找到更恰當的屬性值作為該類的模式，從而有效地提高聚類效果。