一種DS/FH混合擴(kuò)頻的抗干擾波形設(shè)計方法

蔡 武,張世超,邱碩豐,陳凱翔,閔柏成

(中國船舶集團(tuán)有限公司第七二三研究所,江蘇 揚州 225101)

0 引 言

伴隨空間電子對抗技術(shù)領(lǐng)域的不斷發(fā)展進(jìn)步,測控系統(tǒng)需要較為優(yōu)良的抗干擾能力,以滿足空間信息系統(tǒng)的正常運行需求,提高測控系統(tǒng)的抗干擾能力逐漸成為測控領(lǐng)域的重中之重。國內(nèi)外許多學(xué)者為改善測控系統(tǒng)的抗干擾能力進(jìn)行了許多研究工作,主要包括:波形的優(yōu)化設(shè)計、天線的極化處理、波瓣優(yōu)化設(shè)計和信號處理方法等,其中,波形的優(yōu)化設(shè)計是改善測控系統(tǒng)抗干擾能力[1]的重要手段之一。波形的優(yōu)化設(shè)計作為一個頂層的手段,可直接決定測控系統(tǒng)的信號處理方法,并對系統(tǒng)的測量精度、雜波抑制能力及系統(tǒng)本身的分辨力產(chǎn)生直接影響。因此,測控系統(tǒng)的整體構(gòu)建,應(yīng)首先考慮測控信號所采用的模型及其模型本身固有的抗干擾能力,保證測控系統(tǒng)的有效使用,并對測控系統(tǒng)其他環(huán)節(jié)的處理優(yōu)化提供改進(jìn)思路。

為提高測控系統(tǒng)在復(fù)雜電磁環(huán)境中的抗干擾能力,國內(nèi)外專家學(xué)者開展了大量抗干擾信號波形的優(yōu)化設(shè)計工作,使連續(xù)波雷達(dá)發(fā)射的測控信號難以被電子戰(zhàn)設(shè)備捕捉,并能提高測控信號在復(fù)雜電磁干擾環(huán)境中的抗干擾能力,確保測控系統(tǒng)在現(xiàn)代電子戰(zhàn)爭中的技術(shù)優(yōu)勢。抗干擾波形應(yīng)具有較低的截獲概率和較大的信號能量,使其難以被截獲、干擾;同時波形具備較高的參數(shù)測量精度、較小的距離/速度模糊和較好的目標(biāo)分辨力;另外,波形的產(chǎn)生和處理方式上要易于實現(xiàn)。考慮上述幾方面的約束,擴(kuò)頻體制既能滿足航天測控系統(tǒng)抗干擾、抗截獲的要求,又能保證測控信號的高精度和高分辨力。直接序列擴(kuò)頻(DSSS)是現(xiàn)行測控系統(tǒng)中常用的測控體制[2],該體制的信號具有頻譜密度低、抗干擾及抗截獲能力強(qiáng)的特點,實現(xiàn)起來也相對簡單。但伴隨低截獲概率(LPI)信號檢測技術(shù)的不斷發(fā)展進(jìn)步,周期平穩(wěn)隨機(jī)過程及譜相關(guān)理論的不斷完善,該體制下的測控系統(tǒng)受到嚴(yán)重威脅。因此,為進(jìn)一步提高測控系統(tǒng)的抗干擾性能、抗截獲性能,在現(xiàn)有體制的基礎(chǔ)之上,采用性能更優(yōu)的DS/FH混合擴(kuò)頻體制成為當(dāng)前的一種主流趨勢[3]。DS/FH混合擴(kuò)頻體制是在DSSS體制的基礎(chǔ)之上,增加了載波跳變的功能,結(jié)合了2種處理方式的優(yōu)勢,可進(jìn)一步提高測控系統(tǒng)的抗干擾能力[4]。該體制也是目前研究較多的擴(kuò)頻抗干擾技術(shù)。

針對直接序列擴(kuò)頻測控系統(tǒng)的抗干擾能力較差的問題,本文首先通過LAS碼作為DS/FH混合擴(kuò)頻信號的擴(kuò)頻序列,并增加了載波跳變的功能,對信號進(jìn)行建模,然后通過模糊函數(shù)理論,結(jié)合DS/FH混合擴(kuò)頻信號自身特性,分析信號的固有抗干擾性能,最后建立3種常見的壓制式噪聲干擾模型,驗證DS/FH混合擴(kuò)頻信號的抗干擾效果。采用本文所提的波形設(shè)計方法可大大改善匹配接收前后的信干比,滿足測控系統(tǒng)在阻塞式干擾環(huán)境下的抗干擾需求。

1 DS/FH混合擴(kuò)頻信號模型

DS/FH混合擴(kuò)頻體制是在DSSS體制的基礎(chǔ)之上,增加了載波跳變的功能。本文采用LAS(Large Area Synchronized)碼作為DS/FH混合擴(kuò)頻信號的擴(kuò)頻序列[5],LAS碼采用了正交互補(bǔ)碼的設(shè)計理論,通過LA(large-area)碼和LS(Loosely Synchronous)碼的組合編碼方式,形成一種新型編碼,該編碼無干擾窗口。LAS碼的具體產(chǎn)生方式是在LS碼序列組成當(dāng)中插入LA碼,將LA碼與LS碼經(jīng)過某種周期特定的方式聯(lián)合起來。相比于LA碼,LAS碼的占空比較高,且優(yōu)化了無干擾窗口和相關(guān)特性。LAS碼生成示意圖如圖1所示。

DS/FH混合擴(kuò)頻信號在基于LAS碼擴(kuò)頻的基礎(chǔ)之上,采用二進(jìn)制相移鍵控(BPSK)調(diào)制,信號模型為:

(1)

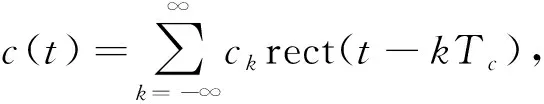
DS/FH混擴(kuò)信號的瞬時自相關(guān)函數(shù)為:

R(τ)=s(t)s(t-τ)=

[cos(ωo+ωk(t))τ+cos(ωo+ωk(t))(2t-τ)]=

P[s1(t)+s2(t)]·[cos(ωo+ωk(t))τ+cos(ωo+ωk(t))(2t-τ)]

(2)

由式(2)可得:

(3)

由式(3)可得單倍載頻和二倍載頻成分的功率譜分別為:

G1(ω)=Pcos(ω0+ωk)τ·[S1(ω)+S2(ω)]

(4)

(5)

DS/FH混擴(kuò)信號瞬時自相關(guān)函數(shù)相應(yīng)的功率譜如下:

G(ω)=G1(ω)+G2(ω)

(6)

通過DS/FH混合擴(kuò)頻系統(tǒng)的模型特征可以看出,混擴(kuò)信號主要成分為載頻跳變的直擴(kuò)信號,其頻譜由若干個直擴(kuò)信號的頻譜組成,一定帶寬的直擴(kuò)信號根據(jù)特定的跳頻圖案,其出現(xiàn)具有偽隨機(jī)性,因此導(dǎo)致每個直擴(kuò)信號在系統(tǒng)總帶寬中僅瞬時覆蓋一小部分。

2 模糊函數(shù)及抗干擾性能分析

模糊函數(shù)(AF)理論拋開了敵方電子戰(zhàn)系統(tǒng)的體制、信號處理手段、截獲及解調(diào)方法等因素,僅從信號固有的特征來分析判斷本身的分辨力、測量精度和抗干擾性能,具有重要的研究意義。

2.1 模糊函數(shù)理論

模糊函數(shù)的數(shù)學(xué)模型[6]為:

(7)

式中:τ為時延;fd為多普勒頻移。

測控系統(tǒng)的信號發(fā)射波形直接影響測量精度、模糊程度、分辨力及抗干擾和抗雜波能力等,而模糊函數(shù)可對分辨率、副瓣特征、距離/速度模糊等方面進(jìn)行有效的定性分析,可直觀地反映發(fā)射波形在距離及速度的二維分辨率及測量精度,充分描述由信號波形所帶來的測量精度及抗干擾和抗雜波能力特性。

在測量精度方面,可通過模糊圖的原點處主響應(yīng)來顯示距離/速度測量精度[7]。距離精度通過時間軸的寬度決定,高的測距精度需要頻域內(nèi)的大時寬分辨力;速度精度通過頻率軸的寬度決定,高的測速精度需要時域內(nèi)具有大時寬分辨力。

在分辨力方面,需具備多目標(biāo)環(huán)境下區(qū)分多個鄰近目標(biāo)的能力。分辨力是由所選波形和信號處理方法決定的。在大信噪比且信號處理系統(tǒng)具有比較優(yōu)良的處理效果時,分辨力僅取決于信號波形的選擇,而信號波形的分辨力可完全取決于模糊函數(shù)圖的中心相應(yīng)寬度。

在模糊程度方面,模糊函數(shù)圖中出現(xiàn)的附加高響應(yīng)情況即為模糊,其大小與原點處的峰值響應(yīng)相當(dāng)。此時,需采取一些有效的措施區(qū)分主響應(yīng)和附加響應(yīng)。

在抗干擾及抗雜波方面,模糊函數(shù)圖的時間、頻率所覆蓋的二維平面會將干擾及雜波與回波信號相重疊,此時即可看出模糊函數(shù)圖中信號波形的抗干擾及抗雜波的能力[8]。若信號波形的抗干擾能力較強(qiáng),則模糊圖中的干擾及雜波響應(yīng)區(qū)域很小,甚至沒有。

2.2 DS/FH混合擴(kuò)頻信號的抗干擾性能分析

通常情況下,針對擴(kuò)頻測控系統(tǒng)的抗干擾性能,主要分析測控系統(tǒng)信息的誤碼率。但在抗干擾評價標(biāo)準(zhǔn)中,誤碼率不作為信號抗干擾的評價準(zhǔn)則[9]。本文從設(shè)計的信號自身特性出發(fā),分析擴(kuò)頻測控信號的固有抗干擾性能,DS/FH混合擴(kuò)頻信號的模糊函數(shù)為:

χ0(τ-mTc,fd+fl-m-fl)+χ0(τ-mTc,fd+fn-fn+m)·

(8)

(9)

由上述模糊函數(shù)的模型可知,DS/FH混合擴(kuò)頻信號的模糊圖為釘床型,相比于直擴(kuò)信號模糊圖中的多間隔離散型旁瓣釘床型,其旁瓣的間隔較低,主要原因在于混擴(kuò)信號中跳頻編碼的加權(quán)作用,抑制了多間隔離散型旁瓣。DS/FH混合擴(kuò)頻信號中,最大無模糊距離為一個包含全部跳頻頻點數(shù)目的混合擴(kuò)頻信號周期長度所能測量的距離,而不再是直接序列擴(kuò)頻中的一個直擴(kuò)偽碼的周期。由于混合擴(kuò)頻信號為一連續(xù)波周期函數(shù),其速度模糊圖為辛克函數(shù),距離分辨力和速度分辨力較高,并且對頻率的調(diào)制沒有帶來距離速度的耦合問題。由上述分析可知,混合擴(kuò)頻信號可用于抗干擾測控中。

2.3 壓制式噪聲干擾模型

所有的雷達(dá)/通信接收機(jī)都無法消除內(nèi)部噪聲,接收機(jī)的內(nèi)部噪聲嚴(yán)重影響測控系統(tǒng)的綜合性能。因此,敵方只需將發(fā)射的干擾信號近似于接收機(jī)的內(nèi)部噪聲,測控系統(tǒng)就很難消除進(jìn)入接收機(jī)的干擾信號。利用噪聲調(diào)制出的干擾信號通常具有以下3個特點:(a)噪聲干擾信號的頻譜較寬;(b)噪聲干擾的功率較大;(c)在時域及頻域上幾乎將目標(biāo)信號完全覆蓋。本文針對下述3種常用的壓制式干擾[10],驗證DS/FH混合擴(kuò)頻信號波形的抗干擾性能。

(1) 射頻噪聲干擾:該干擾又稱為純噪聲干擾,其產(chǎn)生原理是將噪聲源中的射頻噪聲經(jīng)射頻放大器放大后形成的一種壓制式干擾。射頻噪聲干擾的數(shù)學(xué)模型為:

uj(t)=Un(t)cos[ωjt+φ(t)]

(10)

式中:Un(t)為幅度函數(shù),服從瑞利分布;φ(t)為相位函數(shù),服從[0,2π]的均勻分布,且幅度函數(shù)與相位函數(shù)是相互獨立的;ωj為載波頻率,為常數(shù)且遠(yuǎn)大于uj(t)的頻譜寬度,所以射頻噪聲干擾是一種頻率較窄的信號形式。

該干擾的概率分布函數(shù)為正態(tài)分布,從熵譜角度而言,純噪聲干擾的波形較好但干擾電平較低,不適合大功率干擾需求,因此引入噪聲調(diào)幅干擾和噪聲調(diào)頻干擾。

(2) 噪聲調(diào)幅干擾:該干擾是通過噪聲對載波進(jìn)行幅度調(diào)制后形成的一種干擾信號。與射頻噪聲干擾相比,噪聲調(diào)幅干擾也是通過噪聲功率來壓制目標(biāo)信號,區(qū)別在于噪聲調(diào)幅干擾具有一個較強(qiáng)的載波,噪聲調(diào)幅干擾的數(shù)學(xué)模型為:

uj(t)=[U0+un(t)]cosωjt

(11)

式中:un(t)為調(diào)制噪聲;U0一般為常數(shù),代表載波幅度;ωj為載波頻率。

(3) 噪聲調(diào)頻干擾:該干擾是通過噪聲對載波進(jìn)行頻率調(diào)制后形成的一種干擾信號,它同噪聲調(diào)幅干擾一樣具有一個較強(qiáng)的載波,噪聲調(diào)頻干擾的數(shù)學(xué)模型為:

(12)

式中:un(τ)為調(diào)制噪聲;KFM一般為常數(shù),代表調(diào)頻斜率。

3 仿真驗證及分析

3.1 DS/FH混合擴(kuò)頻信號模型仿真

本文通過LAS碼作為DS/FH混合擴(kuò)頻信號的擴(kuò)頻序列,首先需產(chǎn)生LA碼和LS碼序列,然后根據(jù)圖1所示的LAS碼的產(chǎn)生原理,在LA碼中插入LS碼的序列組成,生成LAS碼。

圖2(a)和圖2(b)分別為LA碼自相關(guān)和互相關(guān)特性仿真圖;圖2(c)和圖2(d)分別為LS碼自相關(guān)和互相關(guān)特性仿真圖;圖2(e)和圖2(f)分別為LAS碼自相關(guān)和互相關(guān)特性仿真圖。可以看出,相比于LA碼、LS碼和LAS碼的互相關(guān)特性,3種碼的自相關(guān)函數(shù)在原點處較為尖銳,通過LAS碼作為信號的擴(kuò)頻序列,可在一定范圍之外抑制干擾信號。

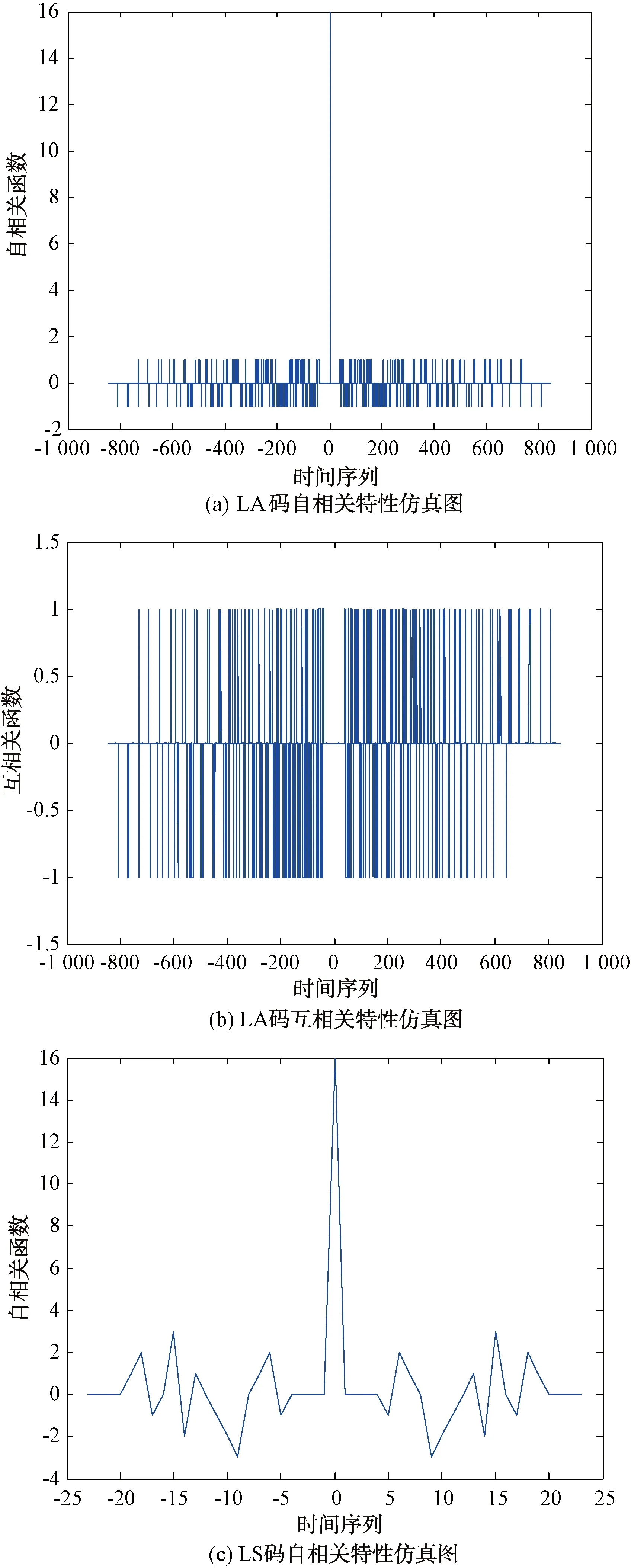
圖2 擴(kuò)頻序列相關(guān)性仿真圖

本文將生成的LAS碼作為DS/FH混合擴(kuò)頻信號的擴(kuò)頻序列,通過設(shè)置調(diào)頻圖案調(diào)制載波信號,進(jìn)而產(chǎn)生DS/FH混合擴(kuò)頻的信號模型。

圖3(a)和圖3(b)分別為DS/FH混合擴(kuò)頻信號的時域波形和頻譜仿真圖;圖3(c)和圖3(d)分別為DS/FH混合擴(kuò)頻信號的自相關(guān)特性和功率譜仿真圖。可以看出,混擴(kuò)信號的波形隨著碼元序列的跳變而變化,信號的頻譜及功率譜與高斯白噪聲相似,在整個頻帶上的分布是比較均勻的;混擴(kuò)信號的自相關(guān)特性表現(xiàn)形式為原點處比較明顯的沖擊函數(shù),其余位置相對平坦且分布均勻,說明該信號具有良好的距離分辨力,進(jìn)而抑制一定范圍之外的干擾信號。

3.2 DS/FH混合擴(kuò)頻信號模糊函數(shù)模型仿真

本文根據(jù)式(8)～(10)所推導(dǎo)的DS/FH混合擴(kuò)頻信號的模糊函數(shù)模型進(jìn)行仿真,可得如圖4所示的信號模糊函數(shù)仿真圖。其中,圖4(a)為DS/FH混合擴(kuò)頻信號的模糊函數(shù);圖4(b)為DS/FH混合擴(kuò)頻信號的一維距離及速度模糊圖。可以看出,DS/FH混合擴(kuò)頻信號的模糊函數(shù)在原點處、時延及多普勒坐標(biāo)軸呈現(xiàn)對稱形狀,且在原點處存在一個尖峰,尖峰附近的旁峰較低,旁峰的走向均沿著時延軸變化較小,不受多普勒軸的變化影響。因此,DS/FH混合擴(kuò)頻信號具有較好的抗干擾性能,在速度軸上無模糊,在距離軸上存在的模糊較小,幾乎可以忽略不計,提高了低截獲性能及測量精度。

3.3 抗干擾性能分析

本文通過對3種常見的壓制式噪聲干擾進(jìn)行仿真,根據(jù)匹配接收的方法,計算匹配接收前后的信干比變化,進(jìn)而分析DS/FH混合擴(kuò)頻信號的抗干擾性能。

圖5(a)和圖5(b)分別為匹配接收前后DS/FH混合擴(kuò)頻信號在射頻噪聲干擾下的時域波形;圖5(c)和圖5(d)分別為匹配接收前后DS/FH混合擴(kuò)頻信號在噪聲調(diào)幅干擾下的時域波形;圖5(e)和圖5(f)分別為匹配接收前后DS/FH混合擴(kuò)頻信號在噪聲調(diào)頻干擾下的時域波形。可以看出,混合信號在匹配接收前,DS/FH混合擴(kuò)頻信號完全被噪聲干擾信號淹沒,混合信號經(jīng)匹配接收后,干擾信號失配,DS/FH混合擴(kuò)頻信號得到匹配,信干比改善明顯。

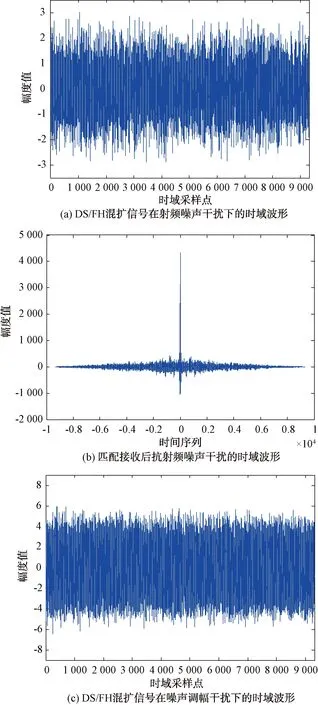
圖5 DS/FH混合擴(kuò)頻信號抗干擾情況仿真圖

為進(jìn)一步分析DS/FH混合擴(kuò)頻信號的抗干擾性能,計算匹配接收前后DS/FH混合擴(kuò)頻信號和直接序列擴(kuò)頻信號(DSSS)的信干比[11]如表1所示。

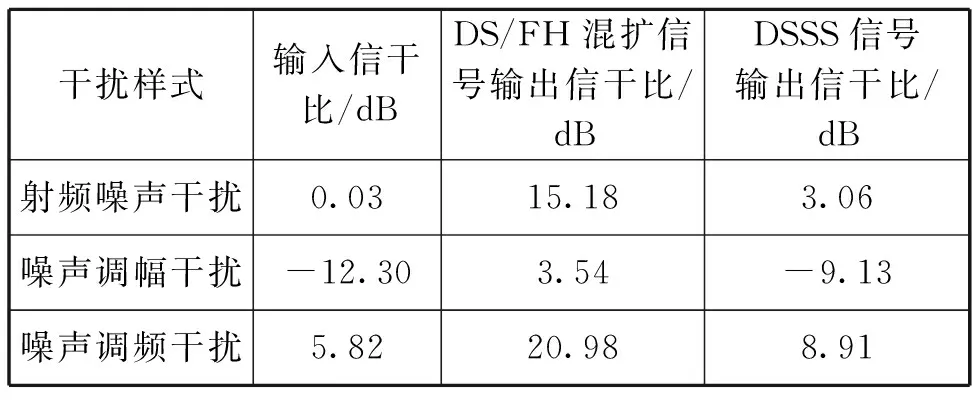
表1 2種信號與干擾匹配接收前后信干比變化

從表1可以看出,DS/FH混合擴(kuò)頻信號抗3種壓制式噪聲干擾的效果較好,經(jīng)匹配接收后信干比分別提高了15.15 dB、15.84 dB和15.16 dB,與DSSS相比,直擴(kuò)信號經(jīng)匹配接收后信干比僅分別提高了3.03 dB、3.17 dB和3.09 dB。結(jié)合圖2(e)和圖3(c)中2種信號的自相關(guān)特性可以看出,相比于DSSS的自相關(guān)特性,DS/FH混合擴(kuò)頻信號的自相關(guān)特性更加優(yōu)良,因此,DS/FH混合擴(kuò)頻信號經(jīng)匹配接收后的信干比改善效果更加明顯。

4 結(jié)束語

直接序列擴(kuò)頻的測控體制實現(xiàn)相對簡單,易于截獲,保密性及抗干擾能力較差。針對此問題,本文采用了一種DS/FH混合擴(kuò)頻的抗干擾波形設(shè)計方法,通過LAS碼作為DS/FH混合擴(kuò)頻信號的擴(kuò)頻序列,并增加了載波跳變的功能,用模糊函數(shù)理論分析信號的固有抗干擾性能。結(jié)合本文的仿真結(jié)果可以看出,采用本文所提的波形設(shè)計方法,信號經(jīng)匹配接收后,信干比得到了良好的改善,測控系統(tǒng)的保密性以及抗干擾能力也得以提高。