全局擾動和互利因子作用的飛蛾撲火優化算法

靳儲蔚，李姍鴻，張琳娜，張達敏+

(1.貴州大學 大數據與信息工程學院，貴州 貴陽 550025；2.貴州大學 機械工程學院，貴州 貴陽 550025)

0 引 言

群智能優化算法[1]是受自然界生物種群的運動、捕食等行為所啟發而提出的一類算法，當前，國內外已經提出了大量的群智能算法，且根據沒有免費的午餐(no-free-lunch，NFL)定理[2]，即過去、現在或未來都不會出現一種算法能夠很好地解決所有的優化問題，因此只有不斷地提出新的群智能算法才能夠解決這些現實優化問題。近幾年已經出現了較多新穎的群智能算法[3-7]，這類算法的使用簡單方便、參數少、運行時間短等特點，為其能夠廣泛運用在實際問題上提供了先決條件。

飛蛾撲火優化(moth-flame optimization，MFO)[8]算法是Mirjalili等提出的新型群智能算法，其基本思想是受飛蛾在夜間飛行所啟發，但同其它智能優化算法相似，MFO算法也具有收斂速度慢、求解的精度不高無法找到理論值、容易陷入局部最優不再隨著迭代的進行向理論更優的位置搜索等問題。在MFO算法提出之后，不斷的有研究者使用MFO算法對工程問題進行優化，文獻[9]使用MFO算法優化認知無線電系統的參數；文獻[10]用差分進化改進的MFO算法求解電力系統負荷經濟調度；文獻[11]使用差分進化改進的MFO算法進行特征選擇。同時也有研究者在其原始算法基礎上進行改進，如文獻[12]將Lévy飛行引入飛蛾撲火優化算法以提高算法的收斂速度和求解精度；文獻[13]將融合折射原理的反向學習引入MFO算法，提高種群的多樣性跳出局部最優解；文獻[14]使用二進制編碼改進MFO算法以解決實際問題，雖然上述改進算法的求解精度和尋優能力相對原始算法有所提升，但其收斂速度以及求解精度仍然存在著較大的改進空間，因此本文提出一種基于全局擾動和互利因子的飛蛾撲火優化算法(DBMFO)。在算法初始化階段使用Bernoulli混沌映射代替原始算法中隨機產生的初始種群，使得初始化的種群具有更優的多樣性；在算法更新公式中增加一個全局擾動因子，增加算法的全局搜索能力，避免算法陷入局部最優；采用互利因子增加種群多樣性，獲得更好的最優解。

1 飛蛾撲火優化算法

飛蛾撲火優化MFO[8]算法是模擬飛蛾在自然界的群體行為而提出的元啟發式智能算法，在MFO算法中，飛蛾飛行的空間即為目標問題的解的空間，一只飛蛾即為目標問題的一個解，火焰的位置即是目標問題的一個較優解，雖然兩者都作為MFO算法中的解，但兩者之間存在區別，火焰的位置代表著MFO局部找到的一個最優位置，在每一次迭代中，飛蛾的位置可能發生改變，但火焰的位置即上一次迭代的最優位置不會隨著飛蛾的飛行而消失。在MFO算法中，飛蛾與火焰的位置分別用矩陣表示，飛蛾和火焰的適應度值分別用向量表示，向量中按適應度值的大小對飛蛾和火焰進行排序，飛蛾位置及火焰周圍空間如圖1所示。

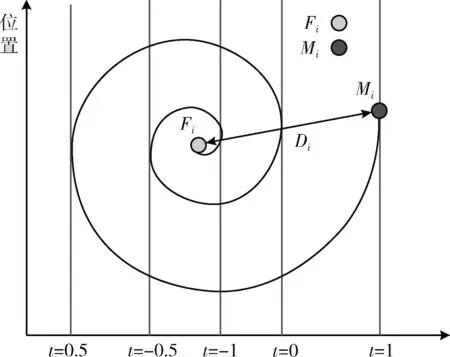
圖1 對數螺旋以及火焰周圍空間

MFO算法中飛蛾的螺旋線飛行更新公式如下

S(Mi，Fj)=Di·ebt·cos(2πt)+Fj

(1)

Di=|Fj-Mi|

(2)

其中，Mi為第i只飛蛾的位置，Fj是第j個火焰的位置，Di為當次迭代中飛蛾與火焰之間的距離，b為對數螺旋線系數，在本文中為1。在更新結束飛蛾的位置之后，使用式(3)使得火焰的數量隨著迭代減少

flameno=round(N-L·N-1T)

(3)

式中：N為最大的火焰數量，L為當前迭代數，T是最大迭代次數，隨著迭代的進行，火焰的數量逐步減少，在迭代末期，飛蛾僅根據最優的火焰位置更新位置。

2 改進的飛蛾撲火優化算法

2.1 Bernoulli混沌映射

目前在群智能算法中使用的混沌映射[15]進行初始化種群，混沌有很多種，其主要使用Logistic混沌映射、Tent混沌映射等[16]，但Logistic映射對初始參數敏感，而且遍歷性較差，而Tent映射的混沌序列又存在小周期、不確定周期點等方面的不足。綜上，本文采用Bernoulli混沌映射來初始化更加均勻的初始種群，相比傳統初始化，使用Bernoulli混沌映射進行初始化可以在搜索空間中遍歷得更加均勻，幫助算法更好的收斂，Bernoulli混沌映射的定義如式(4)

X(i+1)={X(i)1-λ，X(i)∈(0，1-λ]

X(i)-1+λλ，X(i)∈(1-λ，1)

(4)

式(4)中當λ的值取0.5時，混沌性最好。由于MFO算法的模型簡單，參數少，容易實現，而Bernoulli映射遍歷性和隨機性的特點使得算法擁有更加廣泛的搜索范圍。使用Bernoulli混沌映射代替傳統MFO算法的隨機生成初始化種群，提高了種群的多樣性，使得初始的飛蛾種群分布更好，同時讓改進算法有更多機會擺脫局部極值，從而在一定程度上提高了算法的性能。

2.2 全局擾動因子

傳統MFO算法里，算法后期的收斂速度較慢，且隨著火焰數量隨著迭代次數不斷減少，在迭代末期，算法容易受到火焰位置控制，這表明火焰位置會影響每只飛蛾的下一個位置，可知MFO全局搜索能力相對不足，也就是說MFO易陷入之前迭代的局部最優值，為了解決MFO算法的這個缺陷，本節引入全局擾動機制，從而增加飛蛾種群在迭代過程中的多樣性以及隨機性，全局擾動因子μ定義如式(5)所示

μ=tTmax·tanh(1-tTmax)·rand

(5)

其中，t是當前迭代次數，Tmax是MFO算法的最大迭代次數，由式(5)可以看出全局擾動因子的影響，其擾動的趨勢為迭代初期擾動力度逐漸增加，到達迭代中期擾動力度達到頂峰，此時算法的全局搜索能力最好局部搜索能力最弱，最后到迭代末期，擾動力度逐漸降低并且隨著迭代次數到達最大，擾動最后消失，在這一階段算法的全局搜索能力逐漸降低，局部搜索能力逐步提高，且由于每次迭代都會隨機生成一個介于0～1之間的隨機數作為隨機系數對全局擾動因子進行影響，這更增加了全局擾動因子對MFO算法更新公式的影響的隨機性和多樣性。全局擾動因子的變化趨勢如圖2所示。

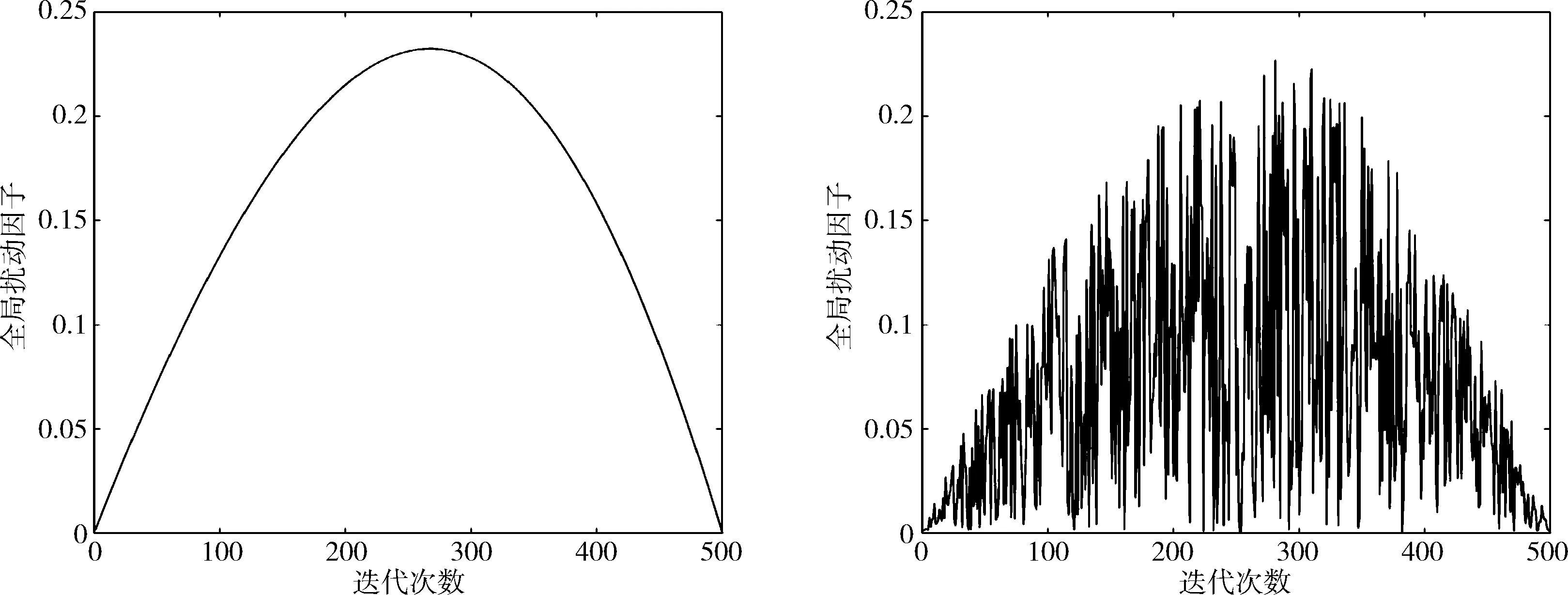
圖2 全局擾動因子μ變化曲線

圖2中，左圖代表沒有受到隨機系數影響的全局擾動因子，其曲線較為光滑，對全局擾動因子的影響缺乏隨機性，右圖代表受到隨機系數影響的全局擾動因子，其隨著迭代次數的增加，按其原有光滑曲線變化的趨勢，不斷波動，使得全局擾動因子更具隨機性與多樣性

S(Mi，Fj)=μ·(Di·ebt·cos(2πt)+Fj)

(6)

式(6)為引入了全局擾動因子后的位置更新公式，與原來位置更新式(1)只使用螺旋線飛行方式產生的新飛蛾位置直接替換原飛蛾位置相比，增加了MFO算法的隨機性和多樣性，以獲得比較不錯的全局最優解。

2.3 互利因子

標準MFO算法的飛蛾的螺旋線飛行更新公式產生的新飛蛾位置直接替換原飛蛾位置，存在以下缺點：第i只飛蛾的位置會根據螺旋線飛行方式選擇第j個火焰的位置和當前種群最優飛蛾位置進行更新，對隨機選擇的第j個火焰的位置個體依賴性較強，缺乏與其它個體學習的部分。在引入了2.2節中所提出的全局擾動因子之后，新的MFO算法的隨機性與多樣性得到了提升，但算法在對于部分測試函數的優化效果欠佳，因此引入互利因子[17]進行完善，互利因子對完成全局擾動后的位置再次進行更新，之后對改進后的新位置與改進前位置進行比較，選擇其間更為優秀的位置，如下

δ=t/Tmax

(7)

b=MA+MB2

(8)

S(Mi，Fj)new=S(Mi，Fj)+δ·(FBest-b·r)

(9)

其中，式(7)的δ為收縮因子，對互利因子更新公式的影響進行收縮，保證更新后的位置處于一個合理的范圍內，避免存在過大的偏差；式(8)中的b為互利因子，代表在搜索空間中，隨機兩個飛蛾的位置的共生量，即通過兩個隨機的位置找到一個新的位置；式(9)為引入了被收縮因子收縮之后的互利因子后的位置更新公式，r為位于區間1到2之間的隨機數，與全局擾動的MFO位置更新式(6)相比，引入收縮因子和互利因子，使其不再局限在前一個火焰位置搜索，即增加了飛蛾的種群多樣性，以獲得最好的全局最優解。

2.4 DBMFO算法步驟

由2.1、2.2、2.3可得基于全局擾動和互利因子的飛蛾撲火優化算法(DBMFO)的步驟如下：

玉皇大帝曾賜給漢人竹片片，讓漢人記錄他們的歷史、言行，也給了傈僳人獐皮，用以寫信等。但是，領獐皮的是一個小孩，他想獐皮這樣笨重難拿，不如吃了還可以飽肚子。于是，在一塊玉米地里偷偷地吃了，回到家里說獐皮被人搶走了，或者在遇到人時說玉帝什么也沒給，因此，傈僳無記錄之紙，也就不能創造文字了。[注]李永憲、馬云喜：《鹽邊縣巖門公社傈僳族調查報告》，編寫組：《四川省苗族傈僳族傣族白族滿族社會歷史調查》，四川省社會科學院出版社，1986年。

步驟1 初始化算法參數，建立搜索空間的矩陣。

步驟2 在搜索空間中使用Bernoulli混沌映射初始化飛蛾種群，計算飛蛾的適應度值并進行排序。

步驟3 使用改進后的更新式(6)對飛蛾的位置進行更新，更新火焰位置及其適應度值。

步驟4 使用互利因子影響的更新位置式(9)對步驟3的結果再一次進行更新，并判斷該步驟是否使飛蛾位置更優秀，若結果更好則使用新的位置，否則保持步驟3的位置。

步驟5 判斷迭代次數是否達到上限，若是則停止迭代，得到最優位置以及其適應度值，否則重復執行步驟3～步驟5，直到滿足終止迭代條件，算法流程如圖3所示。

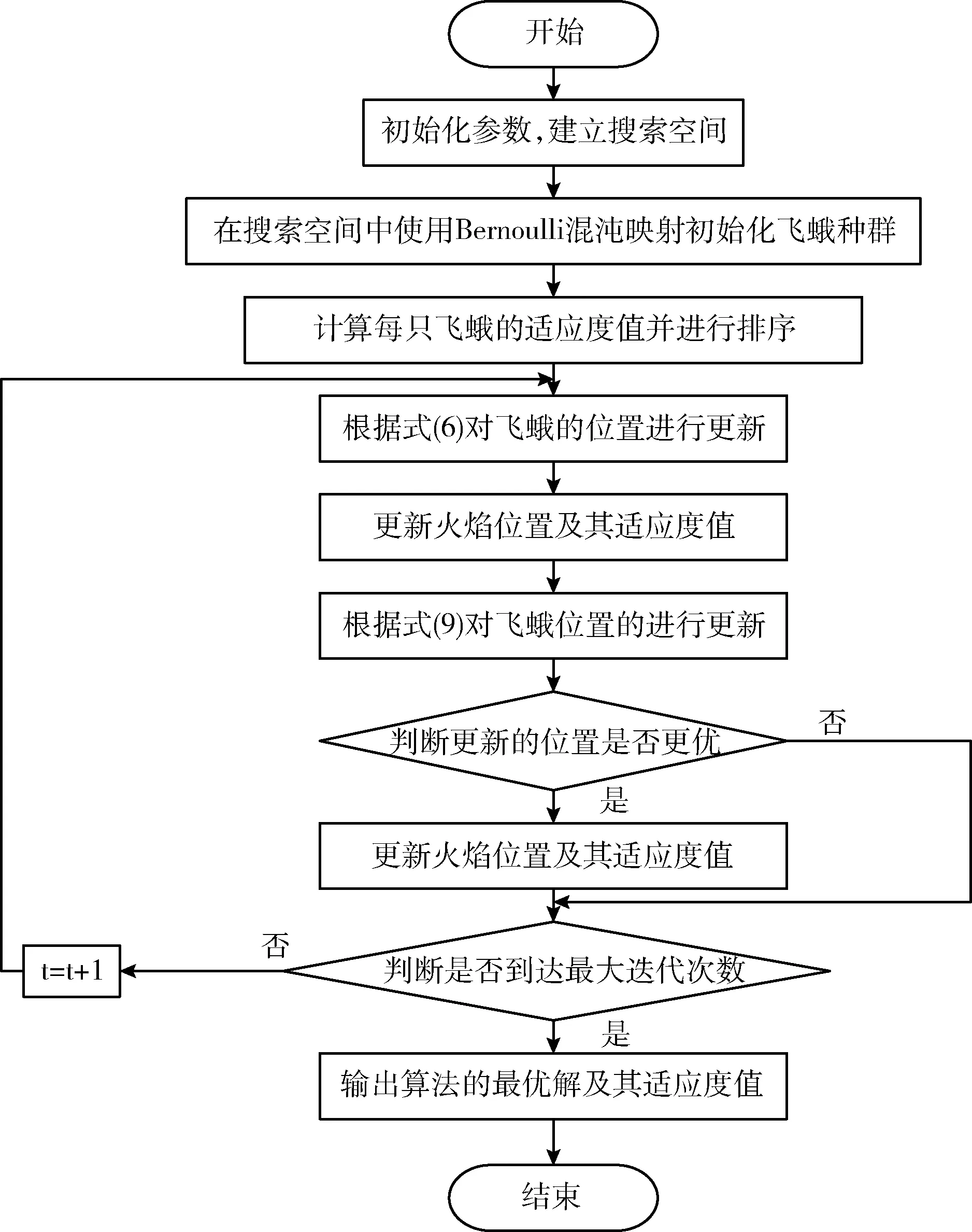
圖3 算法流程

3 仿真實驗和結果分析

3.1 函數選取與參數設置

本文采用MATLAB R2018a進行實驗仿真，運行環境為64位Windows 10操作系統，處理器類型為Intel Core i7-6700。

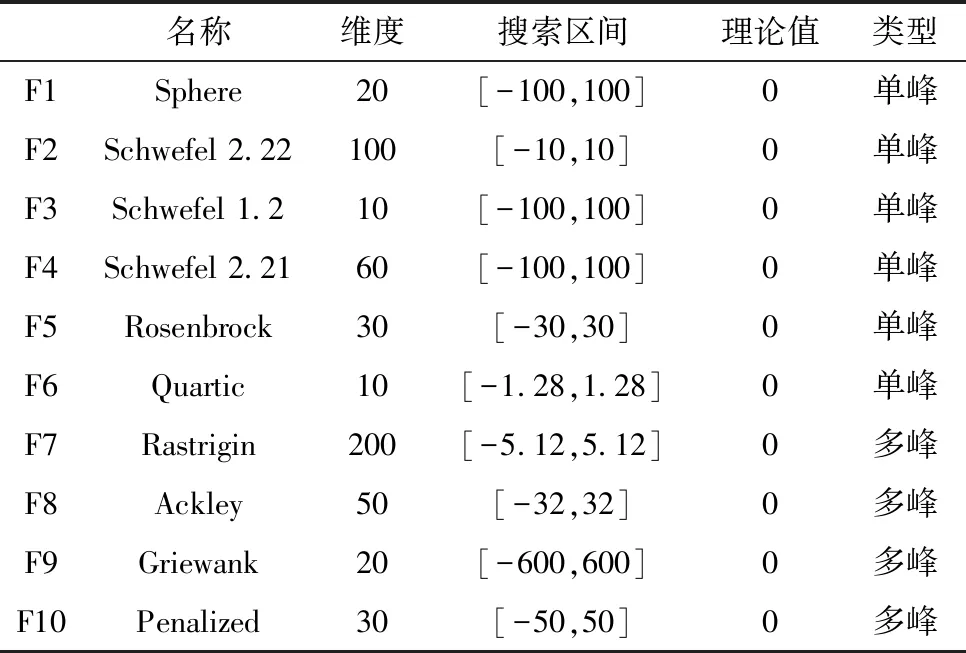
表1 測試函數

實驗中的10個基準測試函數如表1所示。實驗中各算法的基本參數見表2。

表2 算法參數

本文所提出的DBMFO算法同其它傳統算法以及本文提出的各種策略對應的算法相比較的數據結果見表3。

表3 不同算法的結果比較

由表3可以看出，在與其它的傳統群智能優化算法相比時，F1到F4這4個單峰函數上DBMFO算法的表現都是遠超過其它的傳統群智能算法，且其尋優都到達了最優值，且其尋優穩定性好，在30次實驗中均未出現個別尋優值偏離理論值的現象；在F5和F6這兩個單峰函數上，雖然DBMFO算法沒有找到測試函數的理論值，但其優化的精度相比于傳統的MFO算法、SCA、SSA都有至少2個數量級的提升，且相比于優化性能較為優秀的BOA，本文提出的改進算法也能與之優化精度持平；在F7與F9這兩個多峰函數上，DBMFO算法同樣能夠找到測試函數的理論值，值得注意的是雖然函數F7的維度是200維，但DBMFO算法并沒有因此受到過多的影響，同時在尋得理論值的同時，30次數據的標準差為0，即其尋優過程非常穩定；在F8與F10這兩個多峰函數上，雖然DBMFO算法沒有搜索到算法的理論值，但其相比與其它的幾個傳統算法有著較大的改進，其中在F8函數上，在30次實驗中每一次都在迭代后期陷入了局部最優值8.88E-16，其尋優精度相比于除BOA以外的其它傳統算法提高了16個數量級，相比于BOA，其精度提高了7個數量級，在F10函數上其精度相比于BOA以外的其它算法提高了至少7個數量級，對于BOA僅提高了2個數量級；綜上，雖然相比于其它的各種傳統群智能算法DBMFO算法對各個測試函數精度以及穩定性的提升不盡相同，但總的來說，DBMFO算法在求解各種基準函數都具有一定的優勢。

其次，在算法的改進策略里，由表3可以清楚地看到，僅引入全局擾動這一策略主導了DBMFO算法的效果，雖然DMFO算法相比于傳統的MFO算法已經有了相當可觀的精度提升，但其在一些單峰函數上如F2和F4，單一的全局擾動策略在500次迭代下不足以找到測試函數的最優值，在進行進一步測試后發現，DMFO算法在測試函數F2上要達到DBMFO算法所達到的效果在30次實驗里最多需要1195次迭代，在測試函數F4上需要1216次迭代，雖然其500次迭代的精度超過了E-150，但這相比于DBMFO的效果仍有一定的差距，若算法未來解決實際問題，這樣細微的差距可能會造成不利的影響。反觀BMFO算法，從表3可以看到，僅僅使用互利因子對于傳統MFO算法的改進并不明顯，BMFO算法在多峰函數上運行的耗時非常高，且其在測試函數F4上，甚至陷入了局部最優，雖然BMFO對算法的尋優精度和尋優穩定性有著諸多的不利影響，但當互利因子與全局擾動因子相結合后，所得的DBMFO算法在部分函數上的尋優精度以及尋優穩定性取得了明顯的提升，同時，由于全局擾動因子改進后的更新公式更新的位置有利于互利因子的應用，DBMFO算法在高維、多峰的測試函數上的運行并沒有過多的運行時間，其運行時間相比BMFO算法有減少。綜上，全局擾動因子與互利因子的結合是有一定意義且有必要的，改進后的DBMFO算法有效地解決了傳統MFO算法尋優精度、尋優速度、魯棒性不足的缺點。

3.2 測試函數收斂曲線

根據實驗所得數據，各個算法以及策略分別10個測試函數獨立運行30次的平均收斂曲線如圖4所示。

圖4 不同算法的平均收斂曲線

3.3 Wilcoxon秩和檢驗

雖然在30次獨立實驗所得到的平均值與標準差雖然有一定的參考意義，但在多次實驗中，可能會出現某一次實驗的效果極優或極差的情況，這是實驗數據的平均值與標準差無法體現的，因此在評估改進的算法的性能時，僅僅依據平均值與標準差是不夠的，進行統計檢驗來驗證本文所提出的改進算法是非常有必要的，在5%的顯著性水平下進行Wilcoxon秩和檢驗[18]從而判斷DBMFO算法在某些特定問題上有顯著的性能提升。

表4列出所有測試函數中DBMFO算法與其它算法的Wilcoxon秩和檢驗的p值，其中，每個數據代表DBMFO算法與該數據對應的算法在對應的測試函數中相比的p值，由于改進算法無法與算法本身進行比較，因此表中第二列均為N/A，由于p小于0.05即可認為是拒絕零假設的有利證據，即認為“改進算法與其對比的算法是有顯著區別”這一說法是錯誤的概率小于5%，因此，在表中的數據越小就越能夠驗證改進的算法與之對比的算法區別越大，結合表3的數據，即可綜合判斷改進算法的效果，在表中唯有DBMFO算法與BOA在F7上的Wilcoxon秩和檢驗的p值大于0.05，這是由于雖然DBMFO算法在F7上已經穩定尋找到了理論值，但傳統BOA在30次獨立實驗中也有找到理論值，由于秩和測試的定義，兩者數據的差別不太大，因此導致秩和檢驗的p值大于0.05，除此之外，DBMFO算法與其它算法在各個測試函數的Wilcoxon秩和檢驗的p值均小于0.05，驗證本文所提出的改進算法在統計上是具有優越性的。

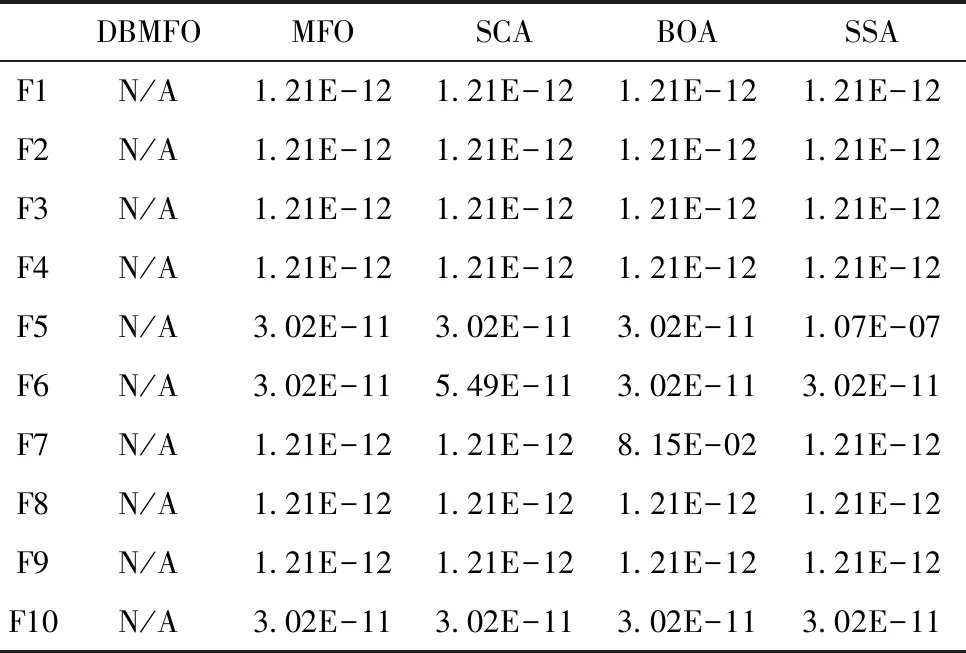
表4 Wilcoxon秩和檢驗的p值

4 結束語

針對傳統MFO算法的缺點，首先引進Bernoulli混沌映射初始化飛蛾種群，使得搜索范圍內種群分布更加均勻，提高種群的多樣性；然后引入全局擾動因子，增加飛蛾種群在迭代過程中的多樣性和隨機性，提高算法的尋優精度和尋優穩定性；最后，使用互利因子與全局擾動因子結合，進一步地提高算法的尋優精度、尋優速度以及尋優穩定性。通過對比實驗證明，改進的算法在具有良好的全局以及局部尋優能力的同時，也具有較好的魯棒性。在未來的研究中，計劃將改進的算法應用于認知無線電系統的參數優化問題上，改進算法的實際應用。