改進(jìn)麻雀算法求解帶模糊需求的低碳路徑優(yōu)化
黃琴,張惠珍,魏欣,鄧歆樂
改進(jìn)麻雀算法求解帶模糊需求的低碳路徑優(yōu)化
黃琴,張惠珍*,魏欣,鄧歆樂
(上海理工大學(xué) 管理學(xué)院, 上海 200093)
針對(duì)低碳背景下帶模糊需求的低碳多式聯(lián)運(yùn)規(guī)劃問題(Low-carbon Multimodal Transportation Planning Problem with Fuzzy Demand, LCMTPP-FD),以成本最小化構(gòu)建數(shù)學(xué)模型。同時(shí),結(jié)合現(xiàn)有的強(qiáng)制碳排放、碳稅、碳交易和碳補(bǔ)償?shù)日邔?duì)LCMTPP-FD進(jìn)行模型轉(zhuǎn)換,研究不同低碳政策對(duì)物流成本和碳排放量的影響。主要根據(jù)模型的特征,設(shè)計(jì)一種分布麻雀搜索算法,對(duì)不同低碳政策下的模型進(jìn)行求解,將迭代次數(shù)作為分布的自由度來提高麻雀算法的性能。將改進(jìn)算法及多個(gè)模型應(yīng)用于實(shí)際運(yùn)輸案例中,改進(jìn)的麻雀算法能在較短時(shí)間內(nèi)獲得最優(yōu)解,并且在強(qiáng)制碳排放下碳排放量最少為9 522.28,在碳交易和碳補(bǔ)償政策下成本分別降低了11.41%、17.24%。改進(jìn)的麻雀搜索算法具有較好的收斂性和搜索能力。強(qiáng)制碳排放能有效地降低碳排放量,碳交易和碳補(bǔ)償能有效降低企業(yè)成本,適合于低碳運(yùn)輸?shù)耐茝V。
低碳多式聯(lián)運(yùn);模糊需求;麻雀搜索算法;自適應(yīng)分布
近年來全球氣候變暖,低碳物流已成為運(yùn)籌優(yōu)化和物流領(lǐng)域的研究熱點(diǎn)之一[1]。國(guó)家倡導(dǎo)調(diào)整運(yùn)輸結(jié)構(gòu),推動(dòng)多式聯(lián)運(yùn),構(gòu)建低碳、經(jīng)濟(jì)和循環(huán)發(fā)展的運(yùn)輸體系。由此,低碳多式聯(lián)運(yùn)規(guī)劃問題(Low-carbon Multimodal Transportation Planning Problem, LCMTPP)成為物流企業(yè)和學(xué)術(shù)界關(guān)注的重點(diǎn)。低碳多式聯(lián)運(yùn)指利用不同運(yùn)輸方式的優(yōu)點(diǎn)將產(chǎn)品從運(yùn)輸起點(diǎn),途經(jīng)若干個(gè)中轉(zhuǎn)節(jié)點(diǎn),運(yùn)往目的地的過程[2]。低碳多式聯(lián)運(yùn)利用不同運(yùn)輸方式的特點(diǎn)進(jìn)行組合,實(shí)現(xiàn)能源充分利用的低碳運(yùn)輸。鄧紅星等[3]考慮了聯(lián)運(yùn)和中轉(zhuǎn)過程中的成本和時(shí)間的影響,構(gòu)建了以成本、碳排放量和運(yùn)輸時(shí)間等目標(biāo)最小化的低碳多式聯(lián)運(yùn)規(guī)劃模型,并采用NSGA-Ⅱ進(jìn)行求解。程興群等[4]分別構(gòu)建了在強(qiáng)制碳排放、碳交易、碳稅和碳中和等政策下考慮道路擁堵情況的多式聯(lián)運(yùn)模型,并基于保優(yōu)策略和移民策略的遺傳算法對(duì)該問題進(jìn)行求解[4]。劉杰等[5]構(gòu)建了總成本和碳排放最小化的多目標(biāo)0-1規(guī)劃模型,并采用改進(jìn)的帶精英策略的NSGA-Ⅱ?qū)δP瓦M(jìn)行求解。
為了將低碳運(yùn)輸推廣至各個(gè)運(yùn)輸企業(yè)中,國(guó)家制定了諸多政策來減少碳排放,實(shí)現(xiàn)綠色運(yùn)輸,如強(qiáng)制碳排放、碳稅、碳交易和碳補(bǔ)償?shù)萚6]。對(duì)于不同的低碳政策,企業(yè)會(huì)選擇不同的運(yùn)輸方案[7]。現(xiàn)有文獻(xiàn)中對(duì)在不同碳政策下帶不確定性條件的低碳多式聯(lián)運(yùn)問題鮮有研究,交通擁堵[4]、天氣和季節(jié)性需求[8]等都會(huì)增加運(yùn)輸?shù)牟淮_定性。王慧等[8]建立了需求模糊且采用集裝箱進(jìn)行運(yùn)輸?shù)亩嗍铰?lián)運(yùn)路徑優(yōu)化模型,并采用粒子群算法和蟻群算法求解該問題。為了使企業(yè)更好地響應(yīng)低碳運(yùn)輸?shù)奶?hào)召和應(yīng)對(duì)環(huán)境變化的不確定性,文中對(duì)帶模糊需求的低碳多式聯(lián)運(yùn)規(guī)劃問題(Low-carbon Multimodal Transportation Planning Problem with Fuzzy Demand, LCMTPP-FD)展開研究。該問題結(jié)合現(xiàn)有主流研究的強(qiáng)制碳排放、碳稅、碳交易和碳補(bǔ)償?shù)鹊吞颊哌M(jìn)行模型轉(zhuǎn)換,制定不同低碳政策下的最佳運(yùn)輸方案。
麻雀搜索算法(Sparrow Search Algorithm, SSA)是由Xue等[9]于2020年首次提出的一種新穎的群集智能優(yōu)化算法。該算法具有收斂速度快、易實(shí)現(xiàn)和參數(shù)少等優(yōu)點(diǎn),已成功應(yīng)用于設(shè)施選址問題[10]、三維路徑規(guī)劃[11]、車間調(diào)度[12]和無人機(jī)航跡規(guī)劃[13]等領(lǐng)域,但在多式聯(lián)運(yùn)方向鮮有應(yīng)用。這里根據(jù)構(gòu)建的模型,將分布模型[14]應(yīng)用于SSA的搜索過程,設(shè)計(jì)了求解不同低碳政策下的LCMTPP-FD的自適應(yīng)分布麻雀搜索算法(Sparrow Search Algorithm with AdaptiveDistribution, ATDSSA)。該算法將迭代次數(shù)作為分布的自由度進(jìn)行變異搜索,該操作不僅避免了SSA易陷入局部最優(yōu),還彌補(bǔ)了該算法易過早收斂的缺陷。最后,在實(shí)際案例中,將原算法和改進(jìn)算法在實(shí)際運(yùn)輸中不同低碳政策下的LCMTPP-FD進(jìn)行求解,以驗(yàn)證模型和改進(jìn)算法的可行性和有效性。
1 帶模糊需求的低碳多式聯(lián)運(yùn)模型
1.1 模糊機(jī)會(huì)約束規(guī)劃

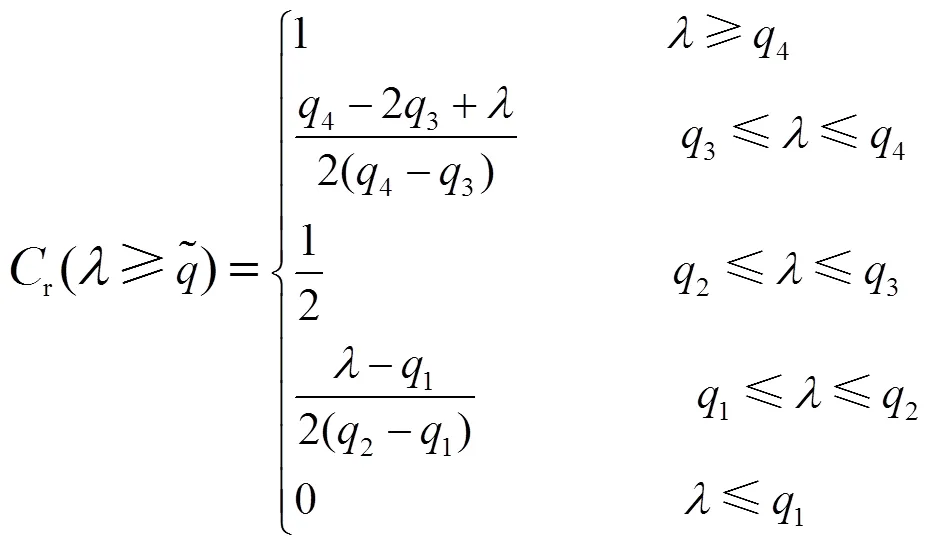
圖1 梯形模糊變量隸屬度函數(shù)
Fig.1 Membership function of trapezoidal fuzzy variable

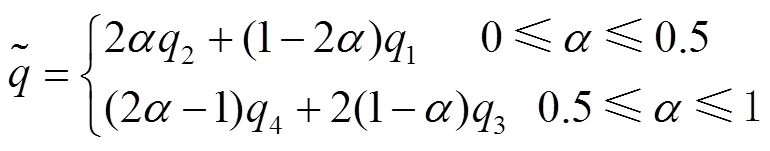
1.2 LCMTPP-FD模型
在某物流企業(yè)的由若干中轉(zhuǎn)節(jié)點(diǎn)和多種運(yùn)輸方式組成的交通系統(tǒng)中,將需求量不確定的貨物從運(yùn)輸起點(diǎn),途經(jīng)若干中轉(zhuǎn)節(jié)點(diǎn),運(yùn)至目的地。同時(shí),為了響應(yīng)國(guó)家低碳運(yùn)輸?shù)奶?hào)召,企業(yè)需在不同碳政策下制定出相應(yīng)的方案進(jìn)行運(yùn)輸。為了便于構(gòu)建模型,給出如下假設(shè):貨物在運(yùn)輸途中不可拆分;在2個(gè)中轉(zhuǎn)節(jié)點(diǎn)間至多選擇1種模式運(yùn)輸;每個(gè)中轉(zhuǎn)節(jié)點(diǎn)至多進(jìn)行1次模式轉(zhuǎn)換;在運(yùn)輸過程中需考慮各路段和節(jié)點(diǎn)的容量限制;不考慮運(yùn)輸過程中天氣、貨損和設(shè)備故障等因素。

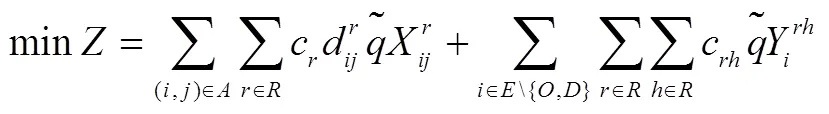
s. t.

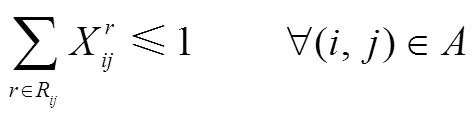

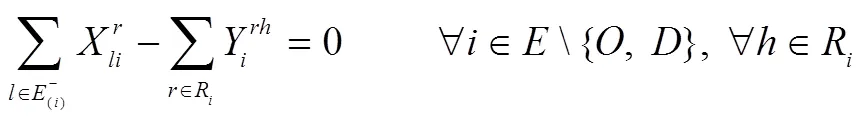
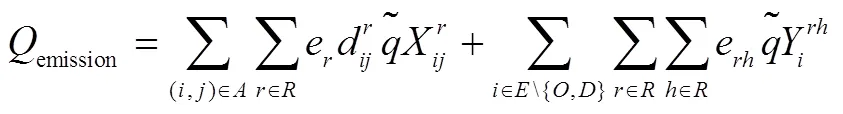
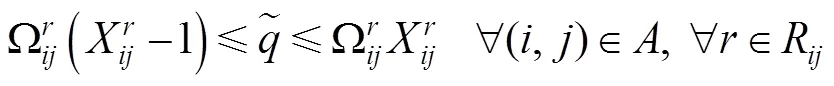
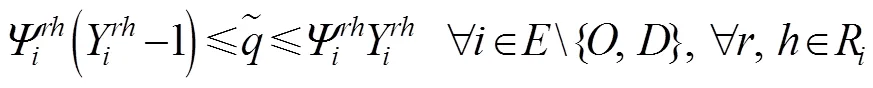

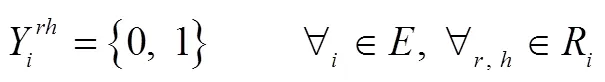
1.3 不同碳政策下的LCMTPP-FD模型
現(xiàn)有的文獻(xiàn)中對(duì)于多式聯(lián)運(yùn)的研究大多數(shù)在確定的環(huán)境中進(jìn)行,但是交通運(yùn)輸系統(tǒng)中包含多種不確定因素,需在需求不確定環(huán)境下進(jìn)行運(yùn)輸任務(wù)的安排。LCMTPP-FD考慮了運(yùn)輸需求的不確定性,并結(jié)合了當(dāng)前多種低碳政策,符合實(shí)際運(yùn)輸。LCMTPP-FD模型分別與強(qiáng)制碳排放、碳稅、碳交易和碳補(bǔ)償?shù)?種政策相結(jié)合,其對(duì)應(yīng)政策下的轉(zhuǎn)換模型依次記為模型Ⅰ、模型Ⅱ、模型Ⅲ、模型Ⅳ,分述如下。
1.3.1 強(qiáng)制碳排放政策下的模型——模型Ⅰ
在強(qiáng)制碳排放政策下,物流運(yùn)輸需嚴(yán)格按照政府的碳排放限制進(jìn)行。由此,約束式(9)應(yīng)滿足該政策下的碳排放額度限制,構(gòu)建模型Ⅰ,見式(14)。

約束式(14)表示運(yùn)輸碳排放量必須小于政府規(guī)定的碳排放量。同時(shí),式(3)—(13)成立。
1.3.2 碳稅政策下的模型——模型Ⅱ

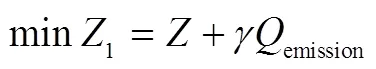
1.3.3 碳交易政策下的模型——模型Ⅲ
碳交易指企業(yè)有一定量的碳排放額度,企業(yè)可根據(jù)實(shí)際運(yùn)輸情況從外購(gòu)買或者出售碳排放額度,在運(yùn)輸完成的同時(shí)盡可能降低成本,模型Ⅲ的構(gòu)建見式(16)。目標(biāo)函數(shù)式(16)表示最小化總物流成本,它包括運(yùn)輸路徑成本、模式中轉(zhuǎn)成本和碳交易成本;式(17)表示碳交易量與實(shí)際排放量之間的關(guān)系;約束式(18)確保碳交易量不低于0,符合實(shí)際情況。同時(shí),約束式(4)—(13)成立。

s. t.
trading+emission=T(17)
T≥0(18)
1.3.4 碳補(bǔ)償政策下的模型——模型Ⅳ
根據(jù)碳補(bǔ)償政策的規(guī)定,如果企業(yè)的碳排放量額度不能滿足實(shí)際運(yùn)輸時(shí),則可從外購(gòu)買,以保證貨物的成功運(yùn)輸。如果企業(yè)完成運(yùn)輸后有剩余的額度,則不可對(duì)外進(jìn)行售賣。LCMTPP-FD在碳補(bǔ)償政策下轉(zhuǎn)換為模型Ⅳ,具體見式(19)—(20)。
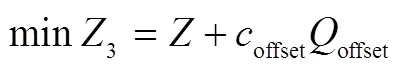
s. t.
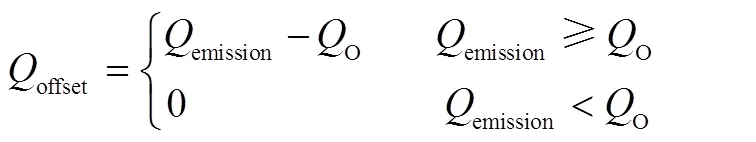
目標(biāo)函數(shù)式(19)表示包含碳補(bǔ)償成本的最小系統(tǒng)總成本,式(20)表示碳補(bǔ)償量由實(shí)際碳排放量和碳補(bǔ)償下配額量之間的關(guān)系決定。同時(shí),約束式(4)—(13)成立。
2 求解LCMTPP-FD的ATDSSA
2.1 麻雀搜索算法
SSA通過模擬麻雀的覓食行為對(duì)解空間進(jìn)行探索,根據(jù)適應(yīng)度的優(yōu)劣程度將適應(yīng)度較優(yōu)的麻雀作為發(fā)現(xiàn)者,負(fù)責(zé)整個(gè)種群食物的搜索,指引雀群的搜索方向。適應(yīng)度較差的個(gè)體為加入者,相較于發(fā)現(xiàn)者,其搜索范圍有限。如果麻雀察覺到危險(xiǎn),則會(huì)通過更新位置進(jìn)行反撲行為。文獻(xiàn)[9]表明,麻雀能夠在發(fā)現(xiàn)者與加入者之間轉(zhuǎn)換。在SSA中,發(fā)現(xiàn)者和加入者的搜索策略分別如式(21)—(22)所示。

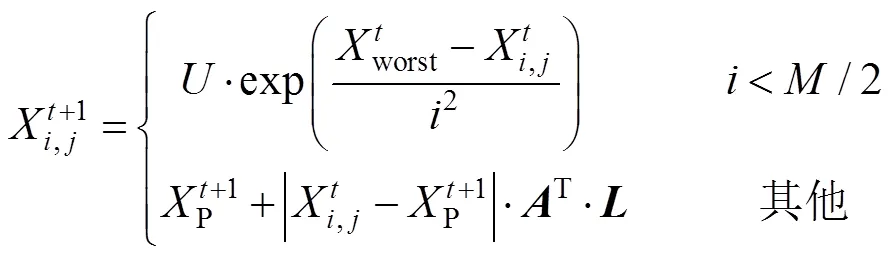
2.2 t分布
分布又稱學(xué)生分布[14],其自由度參數(shù)決定了分布曲線的圖像特點(diǎn)和形態(tài),自由度參數(shù)越小,其曲線變化越平坦,峰值越低,其概率密度函數(shù)根據(jù)式(23)計(jì)算。

2.3 自適應(yīng)t分布麻雀搜索算法
ATDSSA在原SSA的基礎(chǔ)上將算法的迭代次數(shù)作為分布的自由度,對(duì)SSA個(gè)體的搜索策略進(jìn)行擾動(dòng)。在迭代前期,分布趨向于柯西分布變異,其全局搜索能力較強(qiáng);在迭代后期,近似于高斯分布,具有良好的局部探索能力。分布的自由度隨著迭代次數(shù)的變化而不斷調(diào)整,以此平衡局部搜索和全局搜索,加快收斂速度。自適應(yīng)分布更新見式(24)。

這里用分布對(duì)基本的SSA進(jìn)行改進(jìn),首先采用參數(shù)調(diào)優(yōu)方法,即在測(cè)試1個(gè)或1對(duì)參數(shù)對(duì)ATDSSA性能的影響時(shí),其他參數(shù)保持不變,比較不同取值下調(diào)試參數(shù)對(duì)實(shí)驗(yàn)結(jié)果的影響,從而確定算法性能最佳的參數(shù)值。根據(jù)調(diào)試結(jié)果,種群規(guī)模=30,迭代次數(shù)=200,預(yù)警值T=0.6,發(fā)現(xiàn)者和加入者的比例1∶2=0.3∶0.7,發(fā)現(xiàn)危險(xiǎn)程度D=0.2。根據(jù)設(shè)置的參數(shù)隨機(jī)生成初始種群,并計(jì)算每只麻雀的適應(yīng)度值,按升序排列。其次,根據(jù)適應(yīng)度將種群個(gè)體分為發(fā)現(xiàn)者和加入者,分別對(duì)發(fā)現(xiàn)者和加入者進(jìn)行位置更新。最后,當(dāng)分布的密度函數(shù)值大于隨機(jī)數(shù)時(shí)對(duì)種群進(jìn)行分布變異操作。當(dāng)滿足最大迭代次數(shù)時(shí)結(jié)束循環(huán),輸出最優(yōu)解。自適應(yīng)分布麻雀搜索算法具體流程如圖2所示。
圖2 自適應(yīng)t分布麻雀搜索算法流程
Fig.2 Process of sparrow search algorithm with adaptive t distribution
2.3.1 解的表示
采用兩段式自然數(shù)編碼方式,每個(gè)個(gè)體長(zhǎng)度為?1。第1段為長(zhǎng)度的路徑編碼,遍歷過的節(jié)點(diǎn)用其對(duì)應(yīng)的自然數(shù)表示,未遍歷的節(jié)點(diǎn)用0代替。第2段由長(zhǎng)度為?1的模式編碼,1、2、3分別表示公路、鐵路和水路。某10多式聯(lián)運(yùn)網(wǎng)絡(luò)的可行解編碼如圖3所示,該可行解從運(yùn)輸起點(diǎn)出發(fā),依次經(jīng)過節(jié)點(diǎn)3、6、8,到達(dá)目的地,未經(jīng)過節(jié)點(diǎn)2、4、5、7、9。

圖3 某個(gè)體的表示方式
2.3.2 位置更新過程
原始SSA的更新方式適合于連續(xù)優(yōu)化問題。由于這里涉及的各個(gè)節(jié)點(diǎn)為離散分布,因此對(duì)麻雀中的發(fā)現(xiàn)者(加入者)位置更新進(jìn)行改進(jìn),具體步驟如下。
2)從父代從隨機(jī)選擇一個(gè)中轉(zhuǎn)節(jié)點(diǎn)進(jìn)行路徑(運(yùn)輸模式)交叉。
3)調(diào)整交叉節(jié)點(diǎn)前后節(jié)點(diǎn)的連接關(guān)系,使路徑可行。
2.3.3分布變異
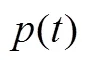
1)計(jì)算出變異節(jié)點(diǎn)采用不同運(yùn)輸模式到各個(gè)后向節(jié)點(diǎn)的局部適應(yīng)度。
2)選擇最小局部適應(yīng)度對(duì)應(yīng)的后向節(jié)點(diǎn)及運(yùn)輸模式作為該變異點(diǎn)的后向局部路徑。
3)將選擇的后向節(jié)點(diǎn)作為新的變異節(jié)點(diǎn),重復(fù)步驟1)—3),直至變異節(jié)點(diǎn)為終點(diǎn)時(shí),結(jié)束循環(huán)。

3 算例分析
為了驗(yàn)證改進(jìn)的算法求解上述模型的有效性,以南寧市到哈爾濱市的實(shí)際運(yùn)輸進(jìn)行計(jì)算。實(shí)驗(yàn)環(huán)境:Windows 11系統(tǒng)下的Matlab 2016a,使用AMD Ryzen 7 5800U with Radeon Graphics、CPU 1.90 GHz、16.0 GB RAM的個(gè)人筆記本電腦。
3.1 算例簡(jiǎn)介
以國(guó)內(nèi)某多式聯(lián)運(yùn)網(wǎng)絡(luò)為例,該運(yùn)輸網(wǎng)絡(luò)涉及南昌、貴陽(yáng)、重慶、南昌、長(zhǎng)沙、武漢、合肥、上海、徐州、濟(jì)南、鄭州、太原、北京、大連和哈爾濱等15個(gè)城市,且分別以、1、2…13和表示。通過輪船票網(wǎng)、火車票網(wǎng)和高德地圖獲得水路、鐵路和公路等運(yùn)輸方式在兩兩城市間不同運(yùn)輸模式對(duì)應(yīng)的距離,如表1所示。
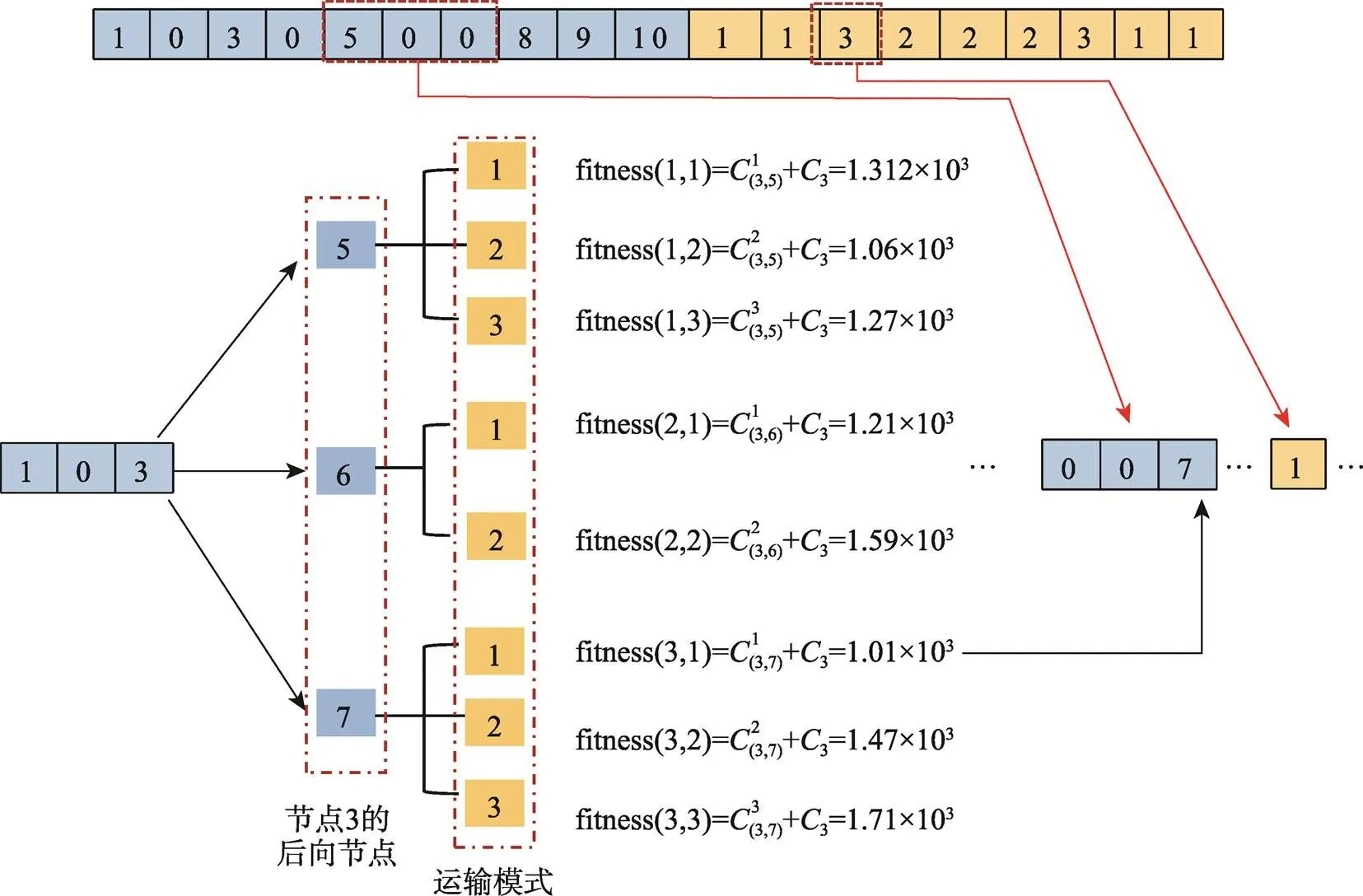
圖4 t分布變異
表1 不同運(yùn)輸方式下兩城市間的距離
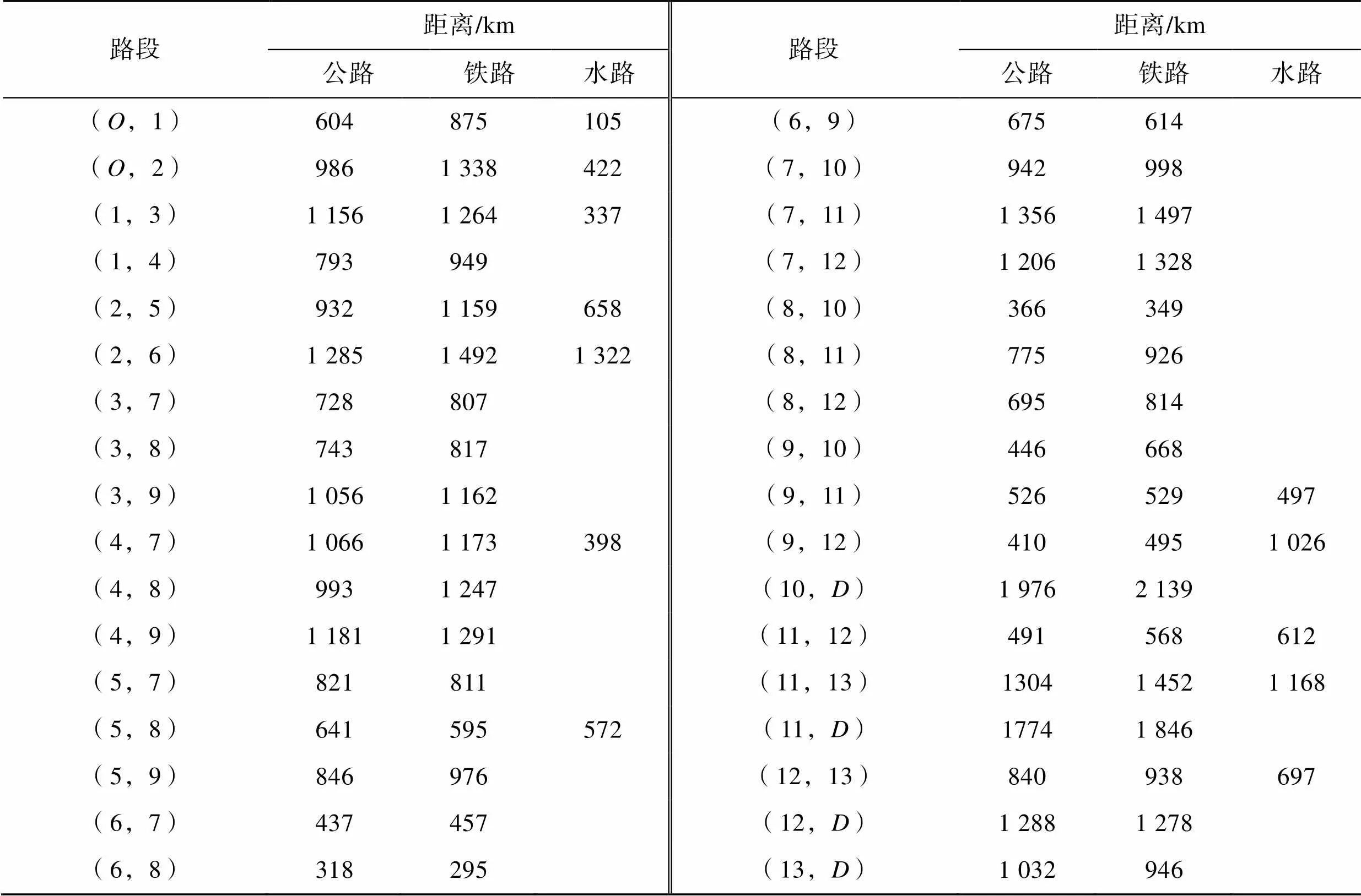
Tab.1 Distance between two cities under different modes of transportation
表2 不同運(yùn)輸方式的參數(shù)

Tab.2 Parameters of different transportation modes
3.2 結(jié)果對(duì)比分析
根據(jù)上述數(shù)據(jù),采ATDSSA、SSA分別對(duì)強(qiáng)制碳排、碳稅、碳交易和碳補(bǔ)償政策下的LCMTPP-FD模型進(jìn)行求解,如表3所示。ATDSSA和SSA在求解強(qiáng)制碳排放和碳稅政策下的LCMTPP-FD均能找到相同的滿意解。同時(shí),不同碳政策下的碳排放量結(jié)果表明,強(qiáng)制碳排放政策有利于減排,且優(yōu)于其他3種政策下的減排效果。由此,在環(huán)境污染較重時(shí)期推行強(qiáng)制碳排放政策有利于減輕環(huán)境污染。ATDSSA在求解碳交易和碳補(bǔ)償時(shí)獲得的結(jié)果中,總成本均為132 946.44,而SSA在碳交易和碳補(bǔ)償下的總成本分別為148 115.19、155 861.72,其增加的成本主要源于節(jié)點(diǎn)3到節(jié)點(diǎn)8或節(jié)點(diǎn)9的模式轉(zhuǎn)換成本,增加了轉(zhuǎn)運(yùn)成本,2個(gè)政策下成本改進(jìn)百分比分別為11.41%、17.24%。在這2種低碳政策下,企業(yè)運(yùn)輸在滿足碳排放約束情況下,為了降低運(yùn)輸成本,會(huì)偏向于選擇ATDSSA獲得的運(yùn)輸方案。由此,在推行低碳初期,碳交易和碳補(bǔ)償可以在一定程度上降低運(yùn)輸成本,利于低碳運(yùn)輸?shù)耐茝V和實(shí)踐。其中,多式聯(lián)運(yùn)路徑中的H、R、S分別表示公路、鐵路和水路運(yùn)輸,見表3。
ATDSSA和SSA在不同低碳政策下獲得的成本和運(yùn)輸所產(chǎn)生的總碳排放量如圖5—6所示,可以發(fā)現(xiàn),在強(qiáng)制碳排放、碳交易和碳補(bǔ)償?shù)日呦逻\(yùn)輸成本明顯低于在碳稅政策下的成本;強(qiáng)制碳排放政策能有效降低碳排放量,利于低碳運(yùn)輸目標(biāo)的實(shí)現(xiàn)。此外,由于這里構(gòu)建的LCMTPP-FD是在成本最小的前提下降低碳排放量,因而ATDSSA在4種低碳政策下的成本均優(yōu)于SSA。由圖6可知,SSA在碳交易和碳補(bǔ)償政策下的碳排放量低于ATDSSA,符合需求主體利益。
為了驗(yàn)證ATDSSA算法在求解LCMTPP-FD的有效性,這里將改進(jìn)的ADTSSA在碳交易政策下的收斂情況與原始的SSA[9]、遺傳算法(Genetic Algorithm,GA)[18]和粒子群優(yōu)化算法(Particle Swarm optimization, PSO)[19]進(jìn)行比較分析。如圖7所示,PSO和SSA的收斂速度較慢,容易陷入局部最優(yōu);ATDSSA和GA均能獲得較好解,但是ATDSSA的收斂速度和初始解的質(zhì)量明顯優(yōu)于GA。將4種算法在同一設(shè)備上迭代200次,其中,GA、PSO、SSA和ATDSSA的運(yùn)行時(shí)間分別為31.4、17.8、20.67、6.22 s。在1個(gè)理想時(shí)間內(nèi),ATDSSA每次迭代獲得的最優(yōu)解明顯優(yōu)于SSA和PSO,且在保證獲得同樣優(yōu)質(zhì)解的同時(shí),ATDSSA所需的計(jì)算時(shí)間更少。由此可見,分布變異操作有效,改進(jìn)算法不僅能節(jié)約時(shí)間,還可有效提高算法性能。
表3 實(shí)驗(yàn)結(jié)果
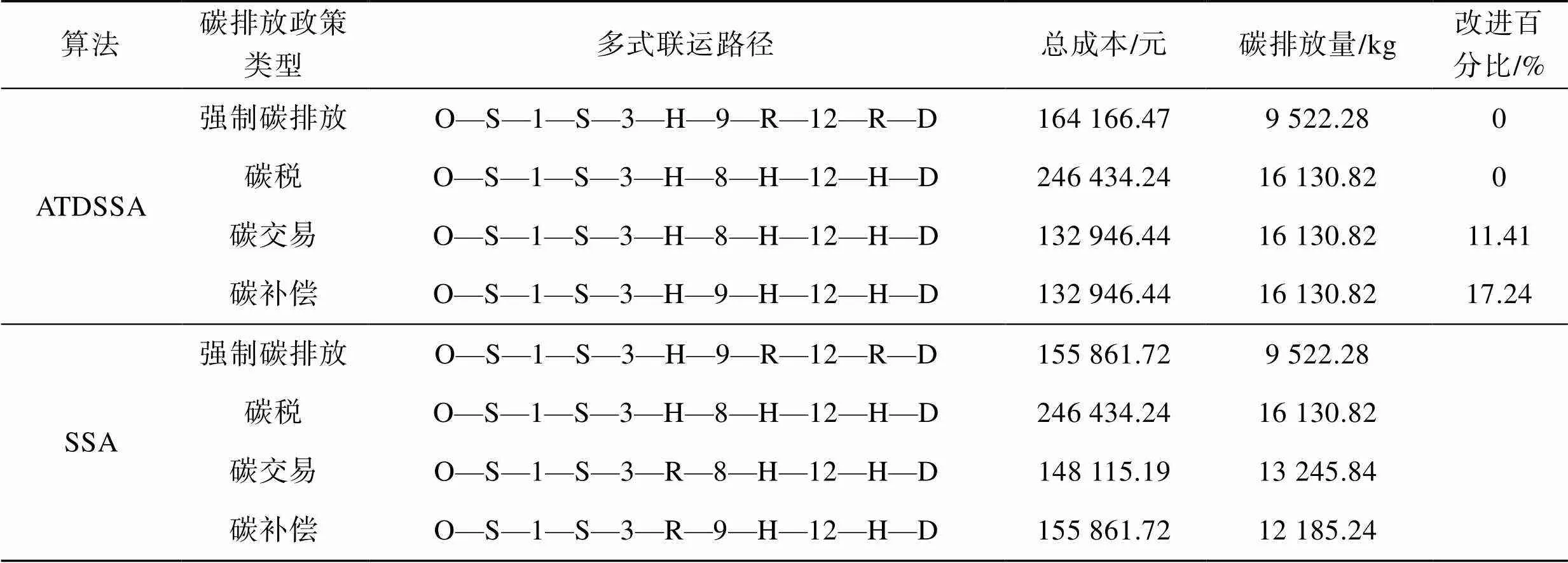
Tab.3 Experimental results

圖5 不同低碳政策下的成本

圖6 不同低碳政策下的碳排放量
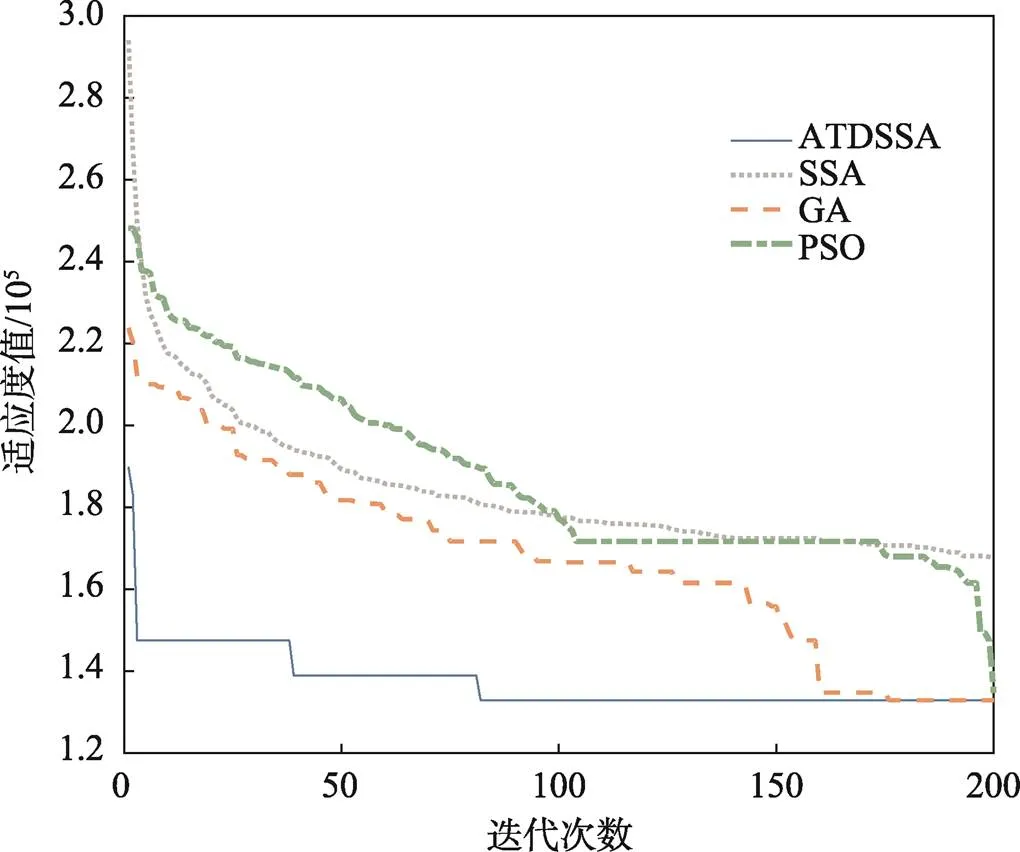
圖7 收斂曲線
4 結(jié)語(yǔ)
針對(duì)不同碳排放政策下帶模糊需求的多式聯(lián)運(yùn)路徑問題,以最小化運(yùn)輸成本、模式轉(zhuǎn)換成本及碳排放成本之和為目標(biāo),構(gòu)建了4種低碳政策下的LCMTPP-FD。構(gòu)建的數(shù)學(xué)模型考慮了環(huán)境變化和實(shí)際情況約束,從而達(dá)到了實(shí)現(xiàn)經(jīng)濟(jì)、低碳運(yùn)輸?shù)哪康摹8鶕?jù)不同的低碳政策模型獲得的結(jié)果表明,強(qiáng)制碳排放政策可以有效降低碳排放量,適合在急需減排的情況下推行;碳交易和碳補(bǔ)償政策對(duì)減少碳排放的力度較小,但可降低企業(yè)成本,適合于低碳運(yùn)輸初期的推廣。LCMTPP-FD為后續(xù)的低碳運(yùn)輸和相關(guān)部門制定政策提供了理論依據(jù)。
通過對(duì)SSA算法進(jìn)行改進(jìn),以迭代次數(shù)作為分布的自由度,以引導(dǎo)雀群進(jìn)行變異搜索,平衡了SSA的全局搜索能力和局部搜索能力,彌補(bǔ)了SSA算法易陷入局部最優(yōu)的缺陷,提高了算法的搜索能力。實(shí)驗(yàn)結(jié)果表明,在算法的搜索能力和收斂性等方面,ATDSSA與SSA、GA和PSO等智能優(yōu)化算法相比,它在運(yùn)行時(shí)間和獲得的解質(zhì)量上都具有較強(qiáng)的競(jìng)爭(zhēng)力。該算法具有較好的性能,可應(yīng)用于離散或連續(xù)的諸多組合優(yōu)化問題研究中,如車輛路徑問題、設(shè)施選址問題和選址路徑問題等。后續(xù)應(yīng)繼續(xù)將該算法應(yīng)用于易腐蝕物品和危險(xiǎn)物品等特殊場(chǎng)景的運(yùn)輸。
[1] 李想, 閔德權(quán), 張祺. 隨機(jī)需求下半開放式冷鏈物流車輛路徑優(yōu)化[J]. 包裝工程, 2022, 43(7): 160-169.
LI Xiang, MIN De-quan, ZHANG Qi. Routing Optimization of Semi-Open Cold-Chain Logistics Vehicle under Random Demand[J]. Packaging Engineering, 2022, 43(7): 160-169.
[2] ZHU C, ZHU X N. Multi-Objective Path-Decision Model of Multimodal Transport Considering Uncertain Conditions and Carbon Emission Policies[J]. Symmetry, 2022, 14(2): 221.
[3] 鄧紅星, 宋雅婧. 考慮碳排放的多式聯(lián)運(yùn)多目標(biāo)路徑規(guī)劃[J]. 重慶理工大學(xué)學(xué)報(bào)(自然科學(xué)), 2022, 36(11): 219-225.
DENG Hong-xing, SONG Ya-jing. Multi-Objective Route Planning for Multimodal Transportation Considering Carbon Emissions[J]. Journal of Chongqing University of Technology (NaturalScience), 2022 36(11): 219-225.
[4] 程興群, 金淳. 低碳政策下考慮道路擁堵的多式聯(lián)運(yùn)路徑選擇問題[J]. 運(yùn)籌與管理, 2019, 28(4): 67-77.
CHENG Xing-qun, JIN Chun. Route Selection Problem in Multimodal Transportation with Traffic Congestion Considered under Low-Carbon Policies[J]. Operations Research and Management Science, 2019, 28(4): 67-77.
[5] 劉杰, 彭其淵, 殷勇. 低碳背景下的多式聯(lián)運(yùn)路徑規(guī)劃[J]. 交通運(yùn)輸系統(tǒng)工程與信息, 2018, 18(6): 243-249.
LIU Jie, PENG Qi-yuan, YIN Yong. Multimodal Transportation Route Planning under Low Carbon Emissions Background[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(6): 243-249.
[6] 楊珺, 盧巍. 低碳政策下多容量等級(jí)選址與配送問題研究[J]. 中國(guó)管理科學(xué), 2014, 22(5): 51-60.
YANG Jun, LU Wei. A Location and Distribution Model with Hierarchical Capacities under Different Carbon Emission Policies[J]. Chinese Journal of Management Science, 2014, 22(5): 51-60.
[7] HOEN K M R, TAN T, FRANSOO J C, et al. Effect of Carbon Emission Regulations on Transport Mode Selection under Stochastic Demand[J]. Flexible Services and Manufacturing Journal, 2014, 26(1): 170-195.
[8] 王慧, 汪傳旭. 模糊需求環(huán)境下集裝箱多式聯(lián)運(yùn)箱型和運(yùn)輸方式的選擇[J]. 公路交通科技, 2012, 29(4): 153-158.
WANG Hui, WANG Chuan-xu. Selection of Container Types and Transport Modes for Container Multi-Modal Transport with Fuzzy Demand[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 153-158.
[9] XUE J K, SHEN B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[10] 羅晴川. 基于改進(jìn)麻雀搜索算法的電動(dòng)汽車充電站選址定容在規(guī)劃區(qū)的應(yīng)用[D]. 大慶: 東北石油大學(xué), 2022: 1-64.
LUO Qing-chuan. Application of Location and Capacity Determination of Electric Vehicle Charging Station Based on Improved Sparrow Search Algorithm in Planning Area[D]. Daqing: Northeast Petroleum University, 2022: 1-64.
[11] 白文杰, 賈新春, 呂騰. 改進(jìn)麻雀搜索算法在三維路徑規(guī)劃中的應(yīng)用[J]. 控制工程, 2022, 29(10): 1800-1809.
BAI Wen-jie, JIA Xin-chun, LYU Teng. Application of Improved Sparrow Search Algorithm in 3D Path Planning[J]. Control Engineering of China, 2022, 29(10): 1800-1809.
[12] LUAN F, LI R T, LIU S Q, et al. An Improved Sparrow Search Algorithm for Solving the Energy-Saving Flexible Job Shop Scheduling Problem[J]. Machines, 2022, 10(10): 847.
[13] 李楠, 薛建凱, 舒慧生. 基于自適應(yīng)t分布變異麻雀搜索算法的無人機(jī)航跡規(guī)劃[J]. 東華大學(xué)學(xué)報(bào)(自然科學(xué)版), 2022, 48(3): 69-74.
LI Nan, XUE Jian-kai, SHU Hui-sheng. A Sparrow Search Algorithm with Adaptive t Distribution Mutation-Based Path Planning of Unmanned Aerial Vehicles[J]. Journal of Donghua University (Natural Science), 2022, 48(3): 69-74.
[14] 周方俊, 王向軍, 張民. 基于t分布變異的進(jìn)化規(guī)劃[J]. 電子學(xué)報(bào), 2008, 36(4): 667-671.
ZHOU Fang-jun, WANG Xiang-jun, ZHANG Min. Evolutionary Programming Using Mutations Based on the t Probability Distribution[J]. Acta Electronica Sinica, 2008, 36(4): 667-671.
[15] LIU B D. Fuzzy Random Chance-Constrained Programming[J]. IEEE Transactions on Fuzzy Systems, 2001, 9(5): 713-720.
[16] SUN Y, ZHANG G J, HONG Z J, et al. How Uncertain Information on Service Capacity Influences the Intermodal Routing Decision: A Fuzzy Programming Perspective[J]. Information, 2018, 9(1): 24.
[17] 袁旭梅, 降亞迪, 張旭. 低碳政策下基于區(qū)間的模糊多式聯(lián)運(yùn)路徑魯棒優(yōu)化研究[J]. 工業(yè)工程與管理, 2021, 26(4): 134-141.
YUAN Xu-mei, JIANG Ya-di, ZHANG Xu. Research on Robust Optimization of Interval-Based Fuzzy Multimodal Transport Paths under Low-Carbon Policies[J]. Industrial Engineering and Management, 2021, 26(4): 134-141.
[18] HOSAGE C M, GOODCHILD M F. Discrete Space Location-Allocation Solutions from Genetic Algorithms[J]. Annals of Operations Research, 1986, 6(2): 35-46.
[19] KANNAN S, SLOCHANAL S M R, SUBBARAJ P, et al. Application of Particle Swarm Optimization Technique and Its Variants to Generation Expansion Planning Problem[J]. Electric Power Systems Research, 2004, 70(3): 203-210.
Improved Sparrow Algorithm for Low-carbon Routing Optimization with Fuzzy Demand
HUANG Qin, ZHANG Hui-zhen*,WEI Xin,DENG Xin-le
(School of Management, University of Shanghai for Science & Technology, Shanghai 200093, China)
For low-carbon multimodal transportation planning problem with fuzzy demand (LCMTPP-FD) under the low-carbon background, the work aims to construct a mathematical model to minimize the cost, and transform the LCMTPP-FD by combining existing policies, such as mandatory carbon emission, carbon tax, carbon trading and carbon offset, so as to study the impact of different low-carbon policies on logistics costs and carbon emissions. According to the characteristics of the model, a sparrow search algorithm withdistribution was designed to solve the model under different low-carbon policies, and the number of iterations was taken as the degree of freedom ofdistribution to improve the performance of the sparrow algorithm. The improved algorithm and several models were applied to a real transportation case. The improved sparrow algorithm could obtain the optimal solution in a short time, and the minimum carbon emission under the mandatory carbon emission was 9 522.28. The costs under the carbon trading and carbon offset policies were reduced by 11.41% and 17.24%, respectively. The experimental results show that the improved sparrow search algorithm has high convergence and search ability. Moreover, mandatory carbon emission can effectively reduce carbon emissions. Carbon trading and carbon offset can reduce the total costs, which are suitable for the promotion phase of low-carbon transportation.
low-carbon multimodal transportation; fuzzy demand; sparrow search algorithm; adaptivedistribution
TP301.6
A
1001-3563(2023)17-0220-09
10.19554/j.cnki.1001-3563.2023.17.027
2023-01-16
國(guó)家自然科學(xué)基金(72101149);教育部人文社會(huì)科學(xué)基金(21YJC630087)
責(zé)任編輯:彭颋

