基于LAWSTAC模型的植物生長(zhǎng)條件下層狀土壤水鹽運(yùn)移的數(shù)值模擬

李睿冉，劉思岐，劉 旭，王均香，宋增偉

（1.山東水利職業(yè)學(xué)院，山東 日照 276826；2.北京市南水北調(diào)團(tuán)城湖管理處，北京 100195；3.日照市土地發(fā)展集團(tuán)，山東 日照 276826；4.日照市國(guó)有大沙洼林場(chǎng)，山東 日照 276826；5.日照市政務(wù)服務(wù)中心，山東 日照 276826）

0 引 言

農(nóng)業(yè)生態(tài)水文模型是改善農(nóng)田的鹽堿化防治和水資源短缺現(xiàn)狀的重要工具[1-3]。對(duì)于層狀土壤來(lái)說(shuō)，由于其水流運(yùn)動(dòng)方式的改變，傳統(tǒng)的用于模擬水分和鹽分在非飽和土壤中運(yùn)移的Richards方程和對(duì)流彌散方程不再適用，許多學(xué)者在傳統(tǒng)方程基礎(chǔ)上進(jìn)行改進(jìn)并探索了新的水鹽運(yùn)移計(jì)算及模擬方法。1997 年黃冠華等[4]利用隨機(jī)方法對(duì)一維和二維層狀土壤的非飽和水分運(yùn)動(dòng)進(jìn)行了模擬。1998 年王全九等[5]在對(duì)層狀土入滲機(jī)制的研究中將層狀土入滲過(guò)程分為兩個(gè)階段，用Green-Ampt 模型描述第一階段均質(zhì)土入滲的入滲過(guò)程，用以砂層的進(jìn)水吸力改進(jìn)的Green-Ampt 模型描述第二階段滲透問(wèn)題。2001 年任理等[6]利用傳遞函數(shù)的方法對(duì)室內(nèi)人工構(gòu)造的兩種非均質(zhì)土柱進(jìn)行了模擬，以此研究穩(wěn)定流場(chǎng)中飽和及非均質(zhì)土壤鹽分優(yōu)先運(yùn)移的隨機(jī)特性。2010 年毛曉敏等[7]根據(jù)土壤水動(dòng)力學(xué)的基本原理，提出了計(jì)算多層土壤穩(wěn)滲率的飽和層最小通量法。為了描述非飽和土壤中水流和溶質(zhì)的運(yùn)動(dòng)，Liu 等[8]根據(jù)土壤介質(zhì)和土壤水流運(yùn)動(dòng)自身的特點(diǎn)建立了活動(dòng)流場(chǎng)模型。活動(dòng)流場(chǎng)模型將分形理論引入連續(xù)性模型，解決了大尺度實(shí)際問(wèn)題，也能捕捉小尺度下流動(dòng)的細(xì)部特征[9]。盛豐等建立了活動(dòng)流場(chǎng)模型下描述和模擬非飽和帶土壤中水流運(yùn)動(dòng)和溶質(zhì)運(yùn)移過(guò)程的控制方程，更好的描述了土壤優(yōu)先流運(yùn)動(dòng)整體的非均勻特征[10]。孫燕等[11]提出了通過(guò)累積入滲量和濕潤(rùn)鋒深度求得模型參數(shù)，還提出了生化黃腐酸在鹽堿土水分入滲條件下的水鹽分布及其對(duì)入滲模型參數(shù)的影響，明晰了對(duì)土壤鹽分降低和水分運(yùn)移的作用效果[12]。

目前層狀土水鹽運(yùn)移研究比較成熟的軟件有HYDRUS 和SWAP 等。HYDRUS 模型是由美國(guó)國(guó)家鹽漬土改良中心(US Salinity Laboratory)開發(fā)的一套用于模擬變飽和多孔介質(zhì)中水分、能量、溶質(zhì)運(yùn)移的新型數(shù)值模擬軟件[13]；軟件在模擬土壤中水分、溶質(zhì)及能量的分布，時(shí)空變化及運(yùn)移規(guī)律方面效果較好，對(duì)于分析農(nóng)田灌溉、施肥、環(huán)境污染等實(shí)際問(wèn)題也有很大的幫助[14]；同時(shí)，HYDRUS可以與其他地下水、地表水模型相結(jié)合，從宏觀上分析水資源的轉(zhuǎn)化規(guī)律。SWAP是由荷蘭瓦赫寧根大學(xué)開發(fā)的，主要用于模擬農(nóng)田尺度水鹽運(yùn)移的軟件，適用于多層土壤，同時(shí)考慮了地下水動(dòng)態(tài)變化的影響；SWAP模型不僅可以模擬土壤水分運(yùn)動(dòng)和溶質(zhì)運(yùn)移，同時(shí)也可以對(duì)土壤中的熱量傳輸、土壤蒸發(fā)、植物蒸騰及作物生長(zhǎng)進(jìn)行模擬[15]。但是HYDRUS 模型缺少作物生長(zhǎng)模擬模塊，SWAP模型的溶質(zhì)運(yùn)移模塊采用的是顯式差分，劃分節(jié)點(diǎn)較粗。因此，應(yīng)用SWAP 和HYDRUS 模型模擬農(nóng)田土壤中水鹽運(yùn)移過(guò)程存在一定的局限性。

以往的研究多是在土質(zhì)差異較小、入滲或蒸發(fā)單一條件下的室內(nèi)土柱試驗(yàn)的數(shù)值模擬，缺少對(duì)強(qiáng)異質(zhì)層狀土壤在植物生長(zhǎng)條件下的水鹽運(yùn)移試驗(yàn)進(jìn)行的數(shù)值模擬。本研究以一維土柱水鹽運(yùn)移試驗(yàn)為基礎(chǔ)[16]，進(jìn)行了表面栽種富貴竹的層狀土水鹽運(yùn)移數(shù)值模擬研究，利用層狀土壤水鹽運(yùn)移模型(Layered Soil Water Solute Transport and Crop Growth Model，LAWSTAC)模擬，可以更好的對(duì)研究自然界中土壤質(zhì)地差異較大的農(nóng)田的鹽堿化防治以及灌溉水的高效利用提供數(shù)據(jù)支持。

1 研究方法及內(nèi)容

1.1 研究方法

本文主要利用LAWSTAC 模型對(duì)表面栽種植物的上細(xì)下粗型異質(zhì)層狀土柱水鹽運(yùn)移規(guī)律和溶質(zhì)運(yùn)移對(duì)變化邊界的響應(yīng)進(jìn)行模擬分析，并分析了在蒸發(fā)條件下不同土壤排列(上粗下細(xì)、上細(xì)下粗)對(duì)土壤中的水鹽動(dòng)態(tài)以及蒸散發(fā)量的影響。LAWSTAC 模型是以土壤水、鹽動(dòng)態(tài)遷移的Richards、CDE 方程和作物生長(zhǎng)的基本原理為基礎(chǔ)，利用有限差分方法構(gòu)建的一維層狀土條件下土壤水鹽運(yùn)移和作物生長(zhǎng)的耦合模型，主要由水分運(yùn)動(dòng)模塊、鹽分運(yùn)移模塊和作物生長(zhǎng)模塊這3個(gè)子模塊組成，模型中考慮了土壤的層狀結(jié)構(gòu)對(duì)土壤水鹽運(yùn)移和作物生長(zhǎng)的影響，并對(duì)有限差分網(wǎng)格中的半節(jié)點(diǎn)參數(shù)采用了算術(shù)平均、幾何平均、調(diào)和平均、間接算術(shù)平均、間接幾何平均、間接調(diào)和平均、三點(diǎn)平均和迎風(fēng)平均等8種不同的平均方式，為土壤水鹽運(yùn)移和作物生長(zhǎng)耦合模擬提供了更多的數(shù)值模擬算法[3,17]。

1.2 研究?jī)?nèi)容

1.2.1 LAWSTAC模型模擬與對(duì)比

本文根據(jù)對(duì)有植物生長(zhǎng)的上細(xì)下粗型強(qiáng)異質(zhì)層狀土建立了LAWSTAC 模型，利用LAWSTAC 模型在土柱水鹽運(yùn)移的試驗(yàn)基礎(chǔ)上進(jìn)行模擬，并與試驗(yàn)結(jié)果進(jìn)行對(duì)比，驗(yàn)證LAWSTAC(Layered soil Water-Solute Transport And Crop growth model)模型對(duì)強(qiáng)異質(zhì)層狀土水鹽運(yùn)移模擬的可靠性，并對(duì)粗質(zhì)土的部分基本水力參數(shù)進(jìn)行敏感性分析。

1.2.2 情景分析

利用LAWSTAC 模型對(duì)植物生長(zhǎng)條件下不同層狀土壤排列的蒸發(fā)過(guò)程進(jìn)行模擬，分別設(shè)置上細(xì)下粗型和上粗下細(xì)型兩種不同排列的土壤，評(píng)價(jià)土壤的不同層狀結(jié)構(gòu)對(duì)植物蒸騰、水分運(yùn)動(dòng)以及鹽分累積的影響。

1.2.3 LAWSTAC模型驗(yàn)證與評(píng)價(jià)方法

LAWSTAC 模型模擬層狀土柱的水鹽運(yùn)移過(guò)程，通過(guò)對(duì)下層河砂的基本水力特性參數(shù)比如α、n進(jìn)行調(diào)節(jié)，從而可以較好的模擬層狀土壤入滲率、累積入滲量、含水率以及鹽分濃度的變化，考慮了非穩(wěn)定流情況以及植物的蒸騰作用對(duì)水鹽運(yùn)移產(chǎn)生的影響。將試驗(yàn)結(jié)果與模擬結(jié)果進(jìn)行對(duì)比分析，利用均方根誤差（RMSE）和決定系數(shù)（R2）來(lái)衡量模擬值和實(shí)測(cè)值[16]之間的符合程度，其中RMSE越接近于0、R2越接近于1表示符合效果越好，通過(guò)分析符合程度驗(yàn)證模型模擬的可靠性。

2 均質(zhì)土和層狀土水鹽運(yùn)移的數(shù)值模擬

2.1 模型建立及參數(shù)的確定

利用LAWSTAC 分別模擬一維均質(zhì)壤土土柱和一維層狀土柱的水鹽運(yùn)移全過(guò)程，模擬深度是50 cm，剖分為51 個(gè)節(jié)點(diǎn)，節(jié)點(diǎn)之間間距為1 cm。模擬過(guò)程中設(shè)置3個(gè)土壤體積含水率和電導(dǎo)率的監(jiān)測(cè)點(diǎn)，深度分別為5 cm、15 cm 和25 cm。入滲過(guò)程中上表面設(shè)置為2 cm薄層積水。

2.1.1 土壤水力特性參數(shù)

模型中需要設(shè)置的參數(shù)有飽和體積含水率θs，殘余體積含水率θr，飽和導(dǎo)水率Ks、經(jīng)驗(yàn)參數(shù)α、n。其中θs和Ks是由試驗(yàn)測(cè)得，l是土柱高度，其余參數(shù)是由人工神經(jīng)網(wǎng)絡(luò)模型調(diào)試得到，調(diào)試后的參數(shù)如表1所示。

表1 土壤水力特性參數(shù)Tab.1 Parameters of soil hydraulic characteristics

2.1.2 溶質(zhì)運(yùn)移參數(shù)

模型是以對(duì)流-彌散方程為基礎(chǔ)的，溶質(zhì)運(yùn)移模型有縱向機(jī)械彌散系數(shù)DL和水中的溶質(zhì)分子自由擴(kuò)散系數(shù)D0兩個(gè)，本研究中縱向機(jī)械彌散系數(shù)DL取10 cm，自由擴(kuò)散系數(shù)D0取2.5 cm/h2。

2.2 均質(zhì)土柱模擬結(jié)果與實(shí)測(cè)結(jié)果對(duì)比

2.2.1 入滲過(guò)程

均質(zhì)土土柱的入滲率、累積入滲量、土壤體積含水率和土壤鹽分濃度隨時(shí)間變化的模擬值與實(shí)測(cè)值[16]的對(duì)比圖，如圖1～圖4所示。從圖1～圖4中可以看出，入滲率及累積入滲量的模擬值與實(shí)測(cè)值[16]符合程度較好，土壤體積含水率與土壤鹽分濃度的模擬結(jié)果與實(shí)測(cè)結(jié)果存在一定的差異，主要表現(xiàn)在：25 cm 層土壤體積含水率在入滲初期的實(shí)測(cè)值[16]變化快于模擬值，鹽分濃度模擬值的變化快于實(shí)測(cè)值[16]是由于壓實(shí)不均導(dǎo)致濕潤(rùn)鋒受空氣阻力影響產(chǎn)生優(yōu)先流。通過(guò)誤差統(tǒng)計(jì)（表2）可知，R2在0.9以上，RMSE最大為0.261 cm。兩者誤差都在可接受范圍內(nèi)，表示LAWSTAC 模型可以較好的模擬入滲過(guò)程中均質(zhì)壤土的水鹽運(yùn)移，模型相關(guān)參數(shù)可以直接用于層狀土土柱的模型中。薄麗媛等人驗(yàn)證了LAWSTAC 模型對(duì)模擬不同灌溉水平下土壤水鹽運(yùn)移與制種玉米生長(zhǎng)的適用性[3]。

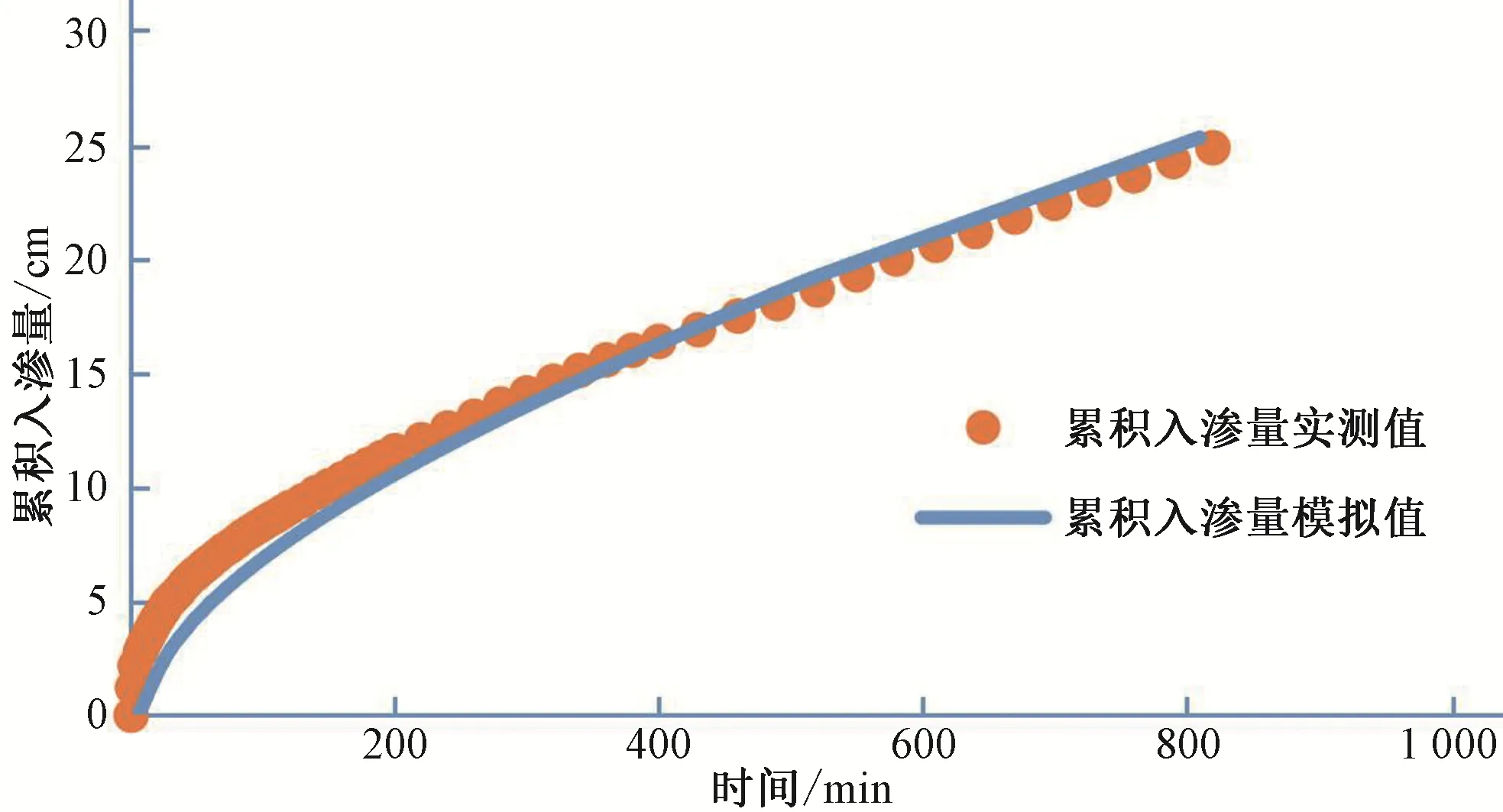
圖1 均質(zhì)土土柱入滲過(guò)累積入滲量模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.1 Comparison between simulated and measured values of cumulative infiltration volume of soil column infiltration in homogeneous soil

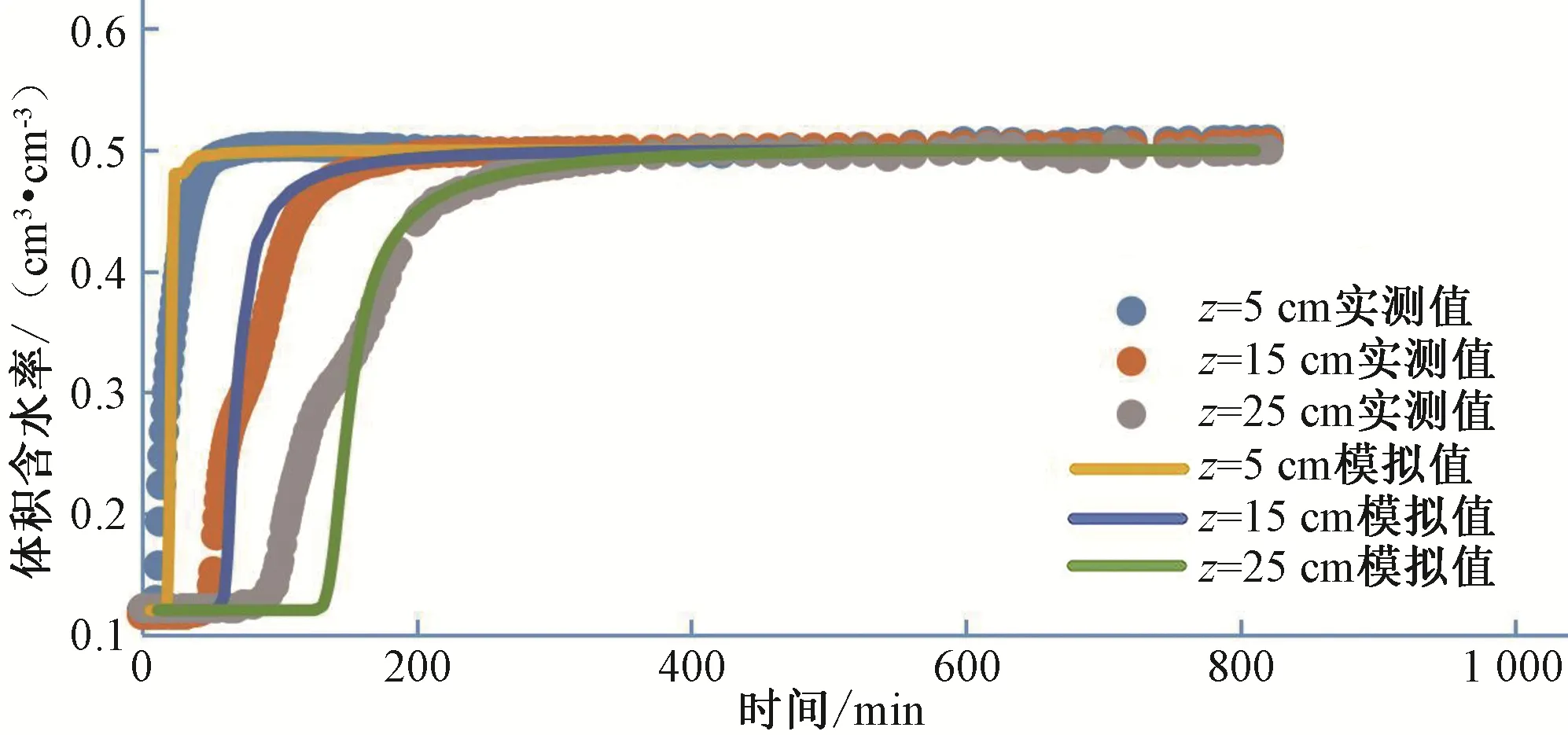
圖3 均質(zhì)土土柱入滲過(guò)程體積含水率模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.3 Comparison between simulated and measured volumetric water content in the process of soil column infiltration in homogeneous soil

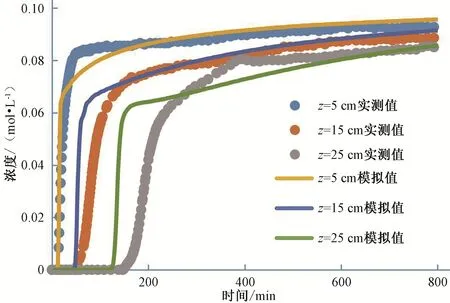
圖4 均質(zhì)土土柱入滲過(guò)程濃度模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.4 Comparison of simulated and measured concentrations in the process of soil column infiltration in homogeneous soil

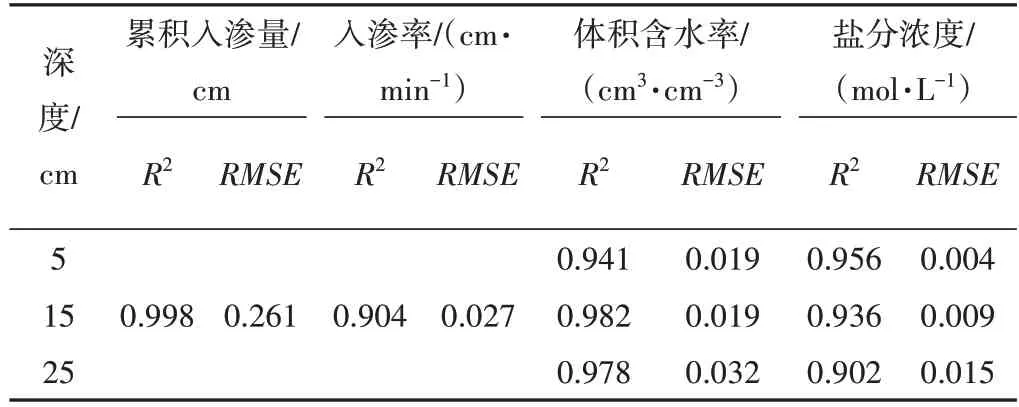
表2 均質(zhì)土入滲過(guò)程模擬效果Tab.2 Simulation of infiltration process of homogeneous soil

2.2.2 蒸發(fā)過(guò)程

均質(zhì)土土柱的蒸發(fā)體積含水率和土壤鹽分濃度隨時(shí)間變化的模擬值與實(shí)測(cè)值[16]的對(duì)比圖，如圖5 和圖6 所示。由圖5和圖6 可見，15 cm 層和25 cm 層水分符合較好，誤差統(tǒng)計(jì)值較為理想（表3），但是5 cm 層水分模擬值與實(shí)測(cè)值[16]不符，原因是實(shí)測(cè)蒸發(fā)過(guò)程中，土壤表面壓實(shí)程度較低，蒸發(fā)過(guò)程中出現(xiàn)裂隙延伸至探頭處，對(duì)體積含水率的測(cè)量造成了影響，導(dǎo)致上層體積含水率測(cè)量出現(xiàn)誤差，下降較快。在鹽分濃度模擬中，鹽分模擬趨勢(shì)與實(shí)際相符，蒸發(fā)過(guò)程中，隨著水分的蒸發(fā)，鹽分濃度應(yīng)該增加，但是在實(shí)測(cè)結(jié)果[16]中鹽分卻是降低的，原因之一是在蒸發(fā)過(guò)程中，土壤中部分鹽分析出，探頭無(wú)法測(cè)得，其二由于土壤三參數(shù)傳感器探頭之間的相互影響，導(dǎo)致測(cè)量出現(xiàn)誤差。

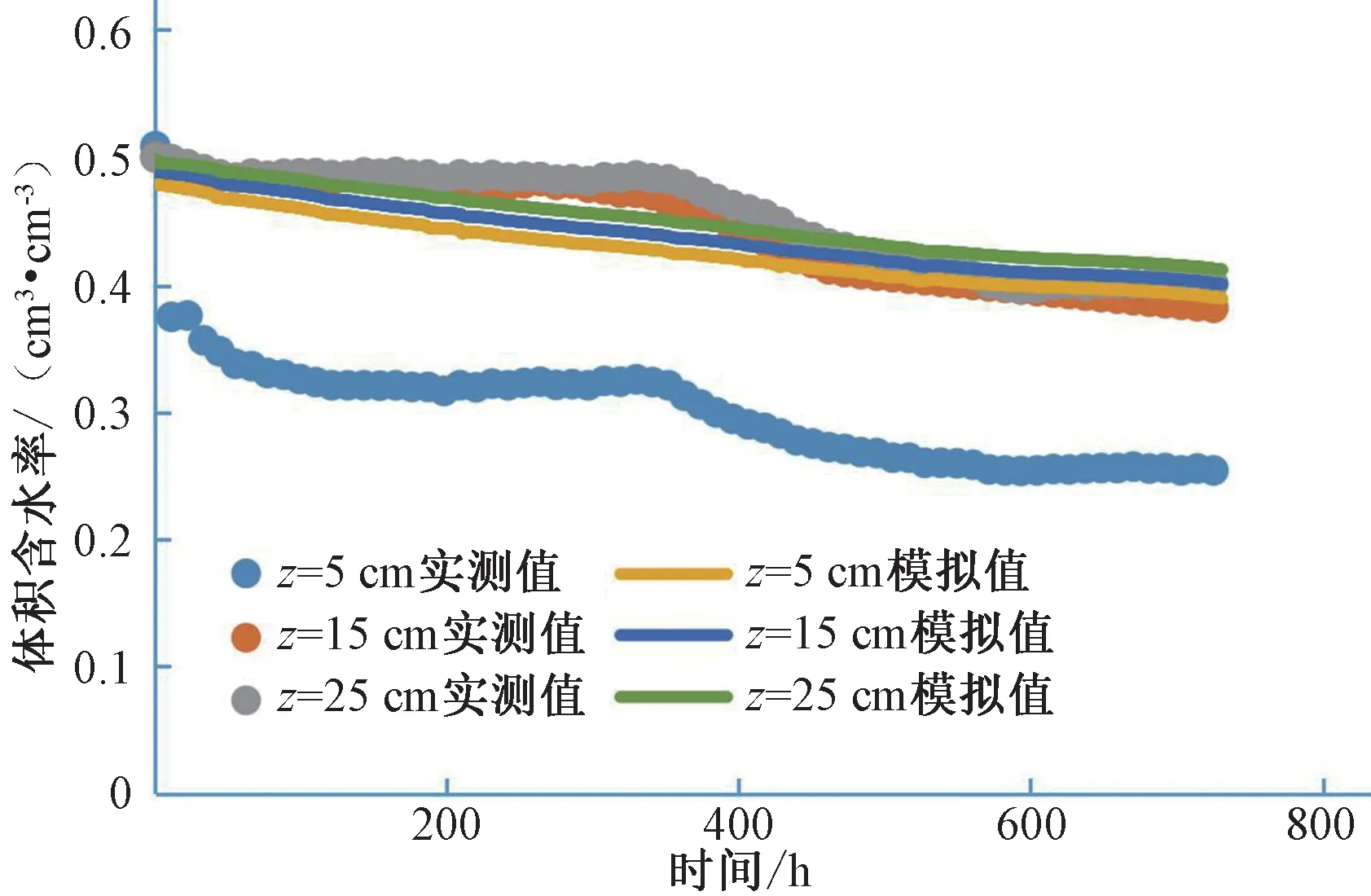
圖5 均質(zhì)土土柱蒸發(fā)過(guò)程體積含水率模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.5 Comparison between simulated and measured volumetric water content during evaporation of soil column in homogeneous soil

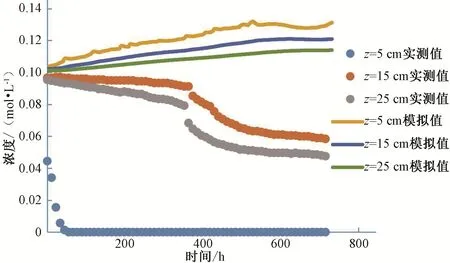
圖6 均質(zhì)土土柱蒸發(fā)過(guò)程濃度模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.6 Comparison of simulated and measured concentrations during evaporation of soil column in homogeneous soil

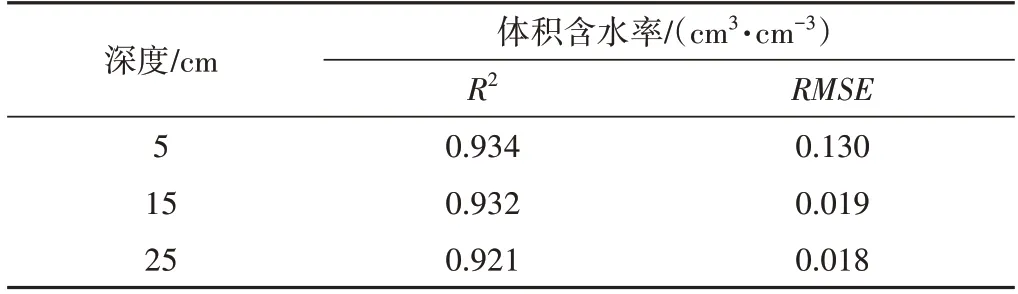
表3 均質(zhì)土蒸發(fā)過(guò)程模擬效果Tab.3 Simulation of evaporation process of homogeneous soil

2.3 層狀土柱模擬結(jié)果與實(shí)測(cè)結(jié)果對(duì)比

2.3.1 入滲過(guò)程

層狀土土柱的入滲率、累積入滲量、土壤體積含水率和土壤鹽分濃度隨時(shí)間變化的模擬值與實(shí)測(cè)值[16]的對(duì)比圖，如圖7～圖10所示。由圖7～圖10可見，由于試驗(yàn)過(guò)程中在土層交界處發(fā)生了指流，導(dǎo)致累積入滲量出現(xiàn)轉(zhuǎn)折，入滲率后期較大，與模擬值符合情況比均質(zhì)土稍差，但是經(jīng)過(guò)誤差統(tǒng)計(jì)（表4），R2在0.8 以上，RMSE最大為0.387 cm，誤差在可接受范圍之內(nèi)。體積含水率和鹽分濃度的模擬值與實(shí)測(cè)值符合程度不理想，尤其是25 cm 層，模擬值變化快于實(shí)測(cè)值[16]，原因是交界面處入滲水流不穩(wěn)定，有指流產(chǎn)生，而且受到上層植物的影響，阻滯了鹽分的運(yùn)移，對(duì)于下層河砂的水力基本參數(shù)把控不佳，造成實(shí)測(cè)值存在誤差，導(dǎo)致入滲過(guò)程中的體積含水率以及濃度模擬值與實(shí)測(cè)值符合程度較差。

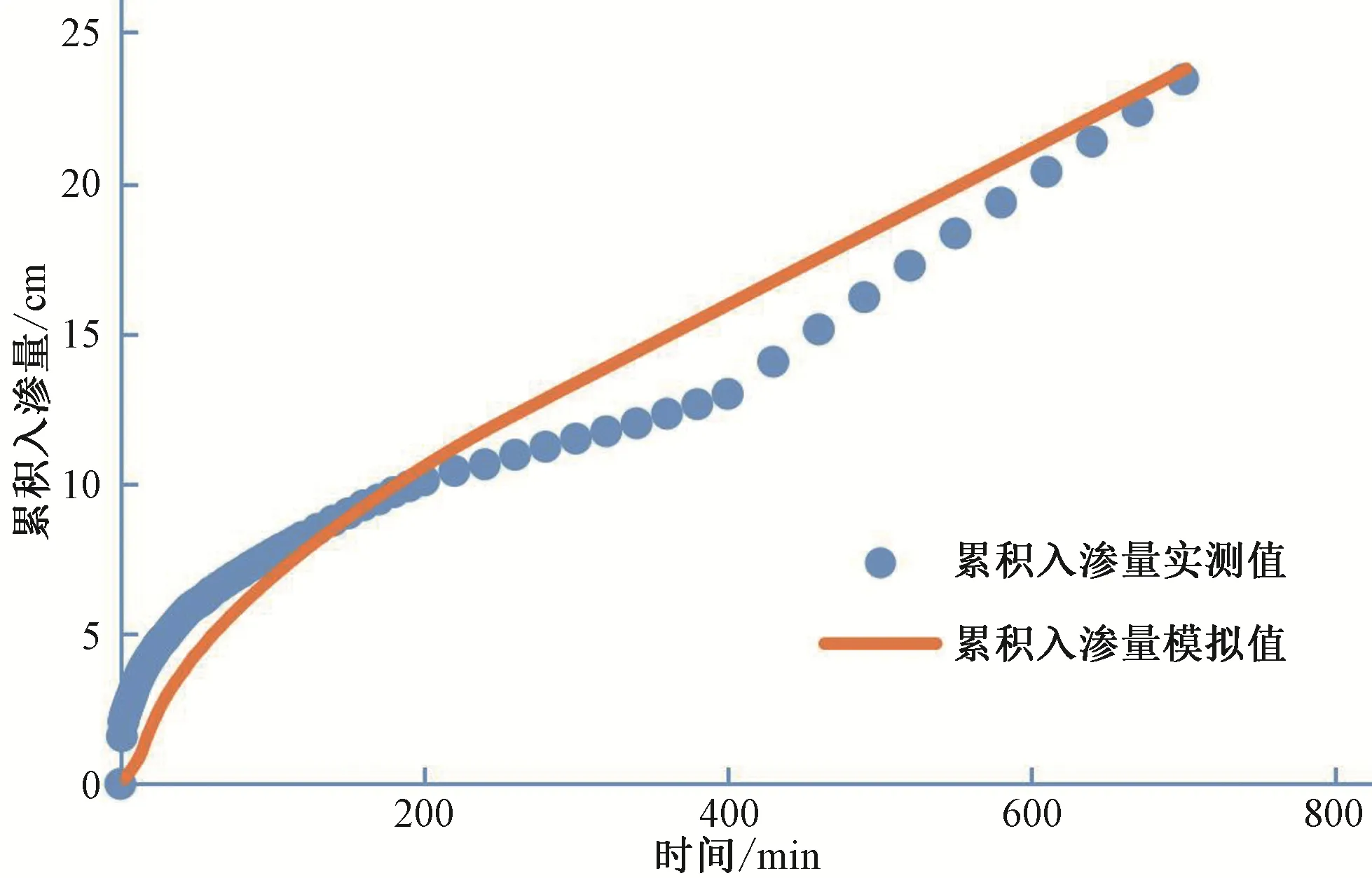
圖7 層狀土土柱入滲過(guò)程累積入滲量模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.7 Comparison results of simulated and measured cumulative infiltration volume in layered soil column infiltration process

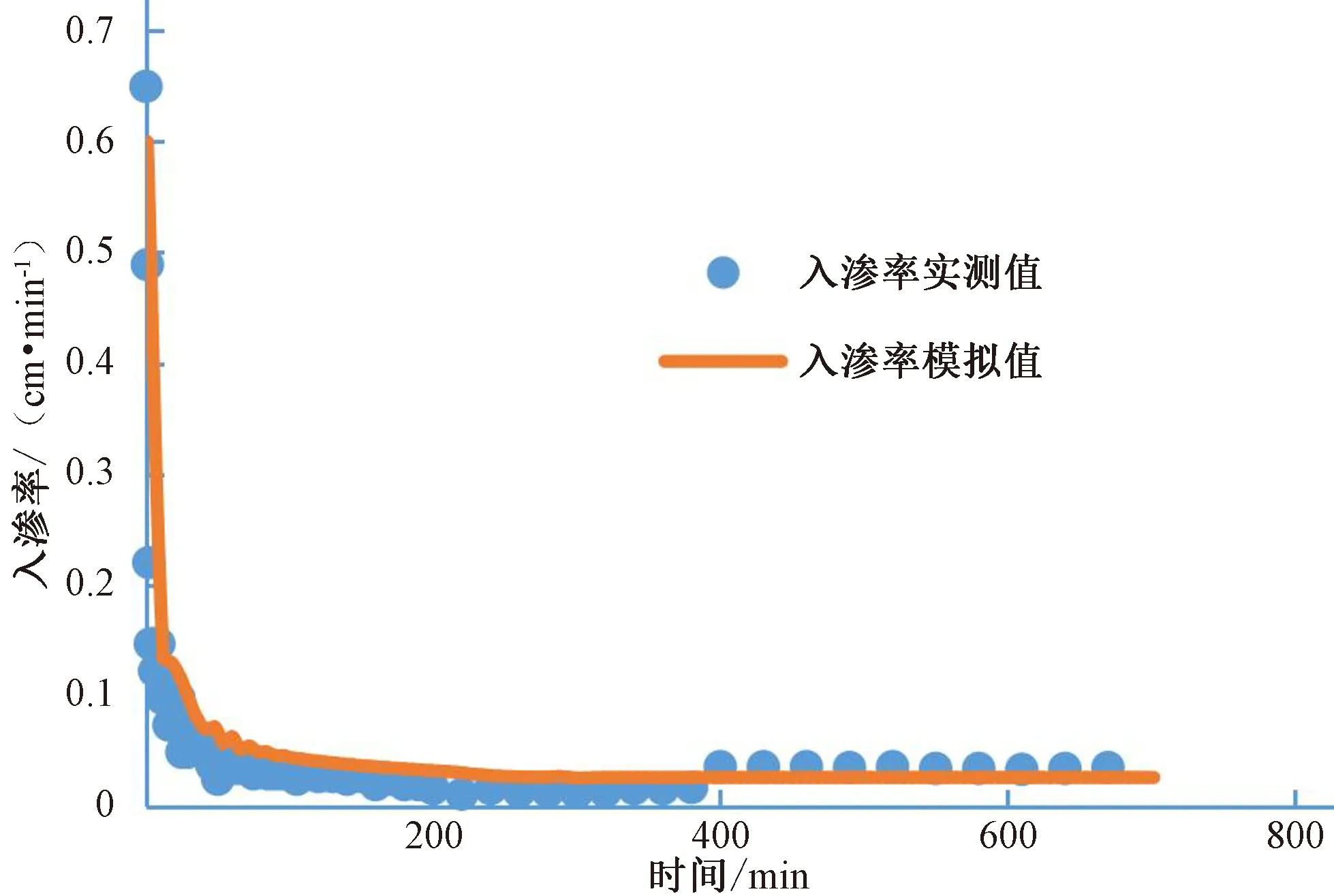
圖 8 層狀土土柱入滲過(guò)程入滲率模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.8 Comparison between simulated and measured infiltration rates of layered soil column infiltration process

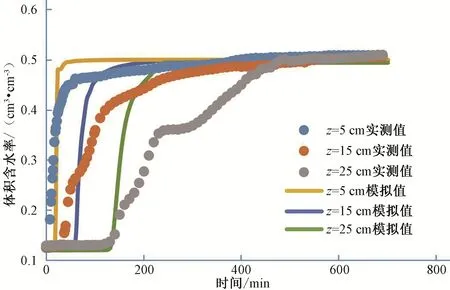
圖9 層狀土土柱入滲過(guò)程體積含水率模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.9 Comparison results between simulated and measured volumetric water content in layered soil column infiltration process

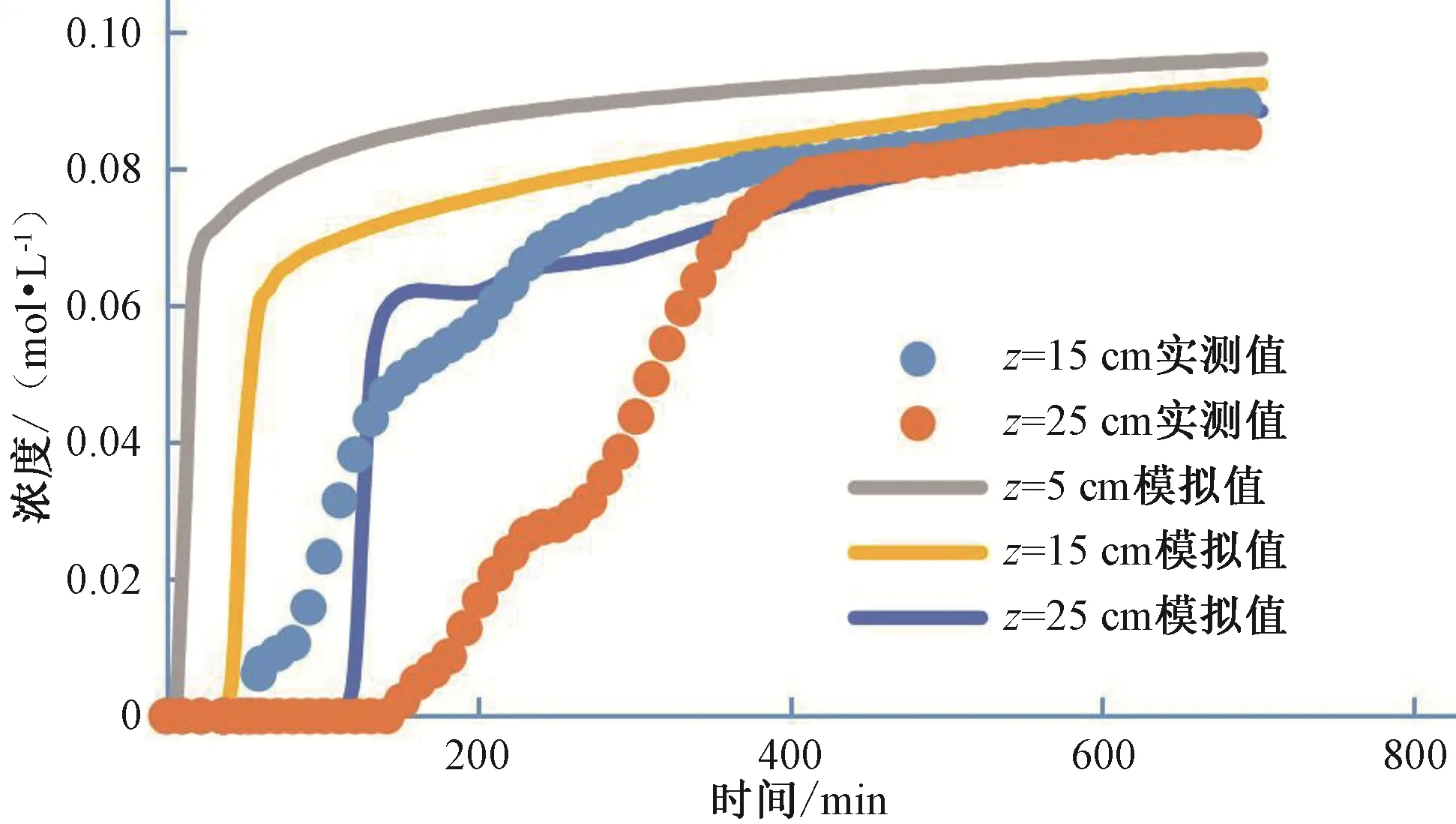
圖10 層狀土土柱入滲過(guò)程濃度模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.10 Comparison between simulated and measured concentrations of layered soil column infiltration process

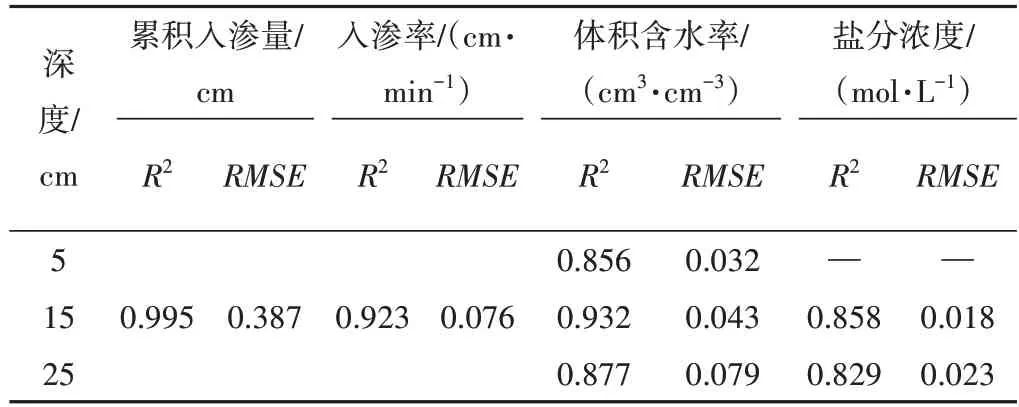
表4 層狀土入滲過(guò)程模擬效果Tab.4 Simulation effect of layered soil infiltration process

2.3.2 蒸發(fā)過(guò)程

層狀土土柱的蒸發(fā)體積含水率和土壤鹽分濃度隨時(shí)間變化的模擬值與實(shí)測(cè)值[16]的對(duì)比圖，如圖11 和圖12 所示。由圖11和圖12可見，100 h以前，除表層外的其他兩層體積含水率符合較好，100 h 之后，實(shí)測(cè)值[16]體積含水率隨時(shí)間減小量增加，與模擬值之間的差距變大，所以之后的符合程度較差。體積含水率100 h 后符合較差的原因之一是由于下層河砂粒徑過(guò)大，不完全符合Richard 方程及對(duì)流彌散方程，利用LAWSTAC 模型模擬的結(jié)果不符合實(shí)際，蒸發(fā)時(shí)，兩層交界以下河砂體積含水率較低，下層基本不向上層供水，導(dǎo)致層狀土壤實(shí)測(cè)體積含水率下降較均質(zhì)土大；其二是對(duì)參數(shù)的把握不好，所以導(dǎo)致差異明顯，于是進(jìn)行了敏感性分析。濃度的實(shí)測(cè)值[16]在5 cm 處無(wú)數(shù)據(jù)，由于鹽分析出，傳感器無(wú)法測(cè)出在含水率較低狀態(tài)下的鹽分，在15 cm 和25 cm 處濃度實(shí)測(cè)值降低。

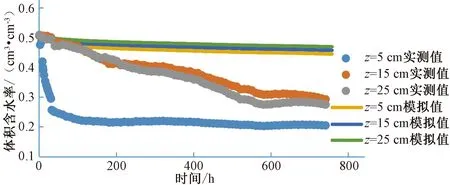
圖11 層狀土土柱蒸發(fā)過(guò)程體積含水率模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.11 Comparison of simulated and measured volumetric water content in the evaporation process of layered soils

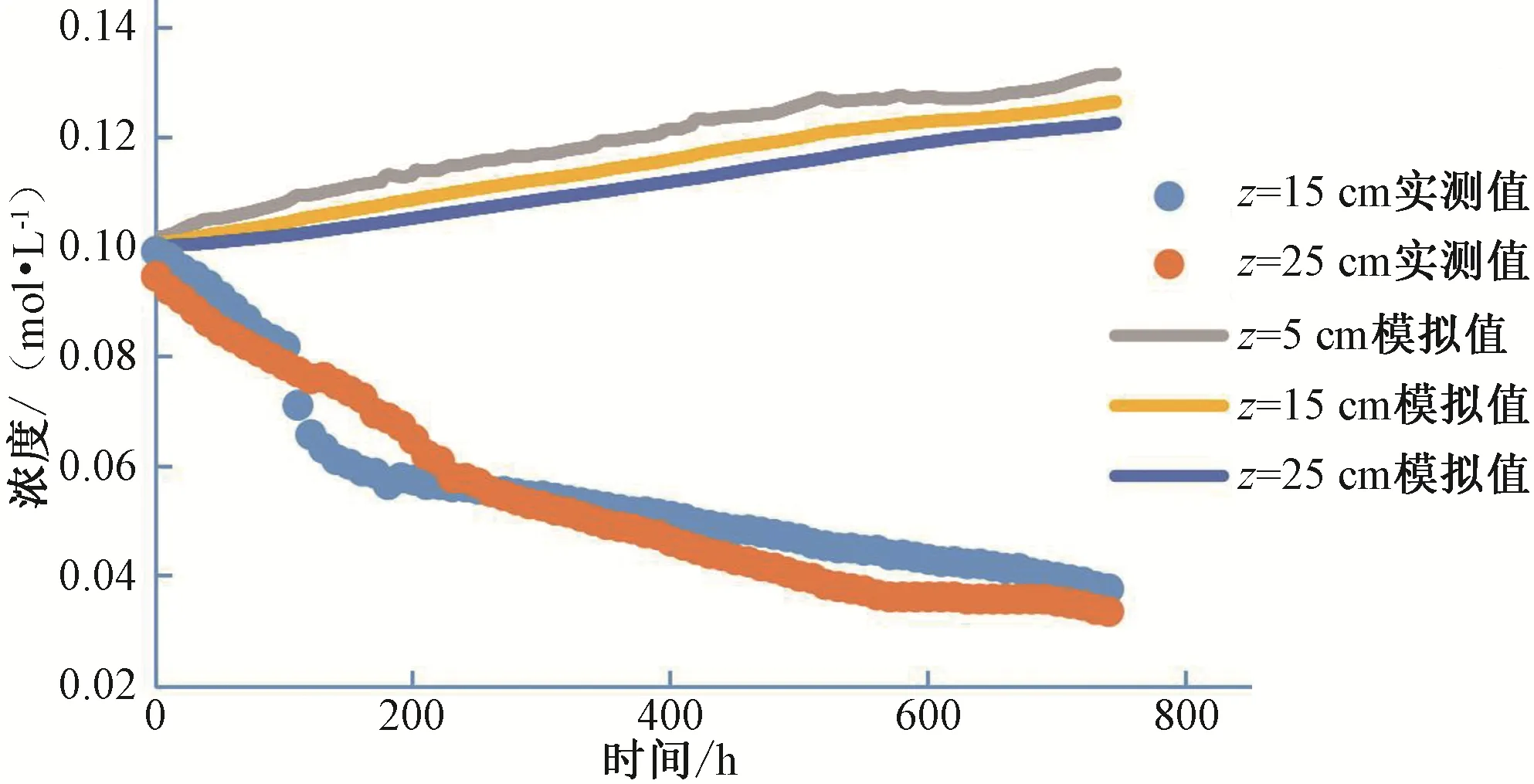
圖12 層狀土土柱蒸發(fā)過(guò)程濃度模擬值與實(shí)測(cè)值對(duì)比結(jié)果Fig.12 Comparison between simulated and measured concentrations of layered soil column evaporation process

2.4 模型敏感性分析

敏感性分析是將模型表示為y=f(x1,x2,…,xn) (xi為模型的第i個(gè)屬性值)，每個(gè)屬性值在可能的取值范圍內(nèi)變動(dòng)，進(jìn)而研究出這些屬性對(duì)模型輸出值的影響程度，這種影響程度大小稱為該屬性的敏感性系數(shù)。敏感性系數(shù)越大，即該屬性對(duì)模型輸出值的影響越大。進(jìn)行敏感性分析的目的主要是分析模型的屬性，求得各屬性的敏感性系數(shù)，在應(yīng)用中主要考慮敏感性系數(shù)大的屬性，減小模型的復(fù)雜程度，從而減輕數(shù)據(jù)分析的工作量，提高模型精度[18]。

由于在層狀土蒸發(fā)過(guò)程中，蒸發(fā)實(shí)測(cè)體積含水率與模擬值符合程度不理想是由于對(duì)下層河砂的水力特性參數(shù)影響的理解不透徹，所以對(duì)層狀土蒸發(fā)條件下河砂的參數(shù)進(jìn)行敏感性分析，以期更好的理解模型結(jié)構(gòu)，發(fā)現(xiàn)模型的缺陷，進(jìn)而對(duì)模型結(jié)構(gòu)進(jìn)行改善。經(jīng)過(guò)對(duì)模型參數(shù)的調(diào)試，發(fā)現(xiàn)下層河砂的α 和n這兩個(gè)經(jīng)驗(yàn)參數(shù)的影響較大，所以本文采用局部敏感性分析法對(duì)蒸發(fā)條件下模型中河砂的參數(shù)α和n進(jìn)行單因素敏感性分析，詳見下式[19]，敏感系數(shù)見表5。

式中：RS為相對(duì)敏感度；x為模型參數(shù)中的某一個(gè)參數(shù)值；Δx為該參數(shù)的改變量；y(x)和y(x+Δx)分別為參數(shù)改變前后的模擬輸出值，包括植物蒸騰量、蒸發(fā)結(jié)束30 cm 根區(qū)儲(chǔ)水量及30 cm 根區(qū)含鹽量。RS越大即該參數(shù)的敏感性越大。將α和n的值分別減少或增加50%、40%、30%、20%、10%，而其他的參數(shù)保持原值不變。然后將變化的參數(shù)代入模型，求解得出相應(yīng)輸出值。

通過(guò)表5 可以看出，蒸發(fā)過(guò)程中，植物出現(xiàn)了水分脅迫。對(duì)于植物蒸騰量來(lái)說(shuō)，增大α值對(duì)其影響不大，增大n值幾乎無(wú)影響，但是減小n值對(duì)其影響很大，且減小幅度越大，敏感性系數(shù)越大。說(shuō)明蒸發(fā)過(guò)程中，河砂孔隙度越小，水分脅迫越明顯。基本水力特性參數(shù)α越大，對(duì)于30 cm 根區(qū)儲(chǔ)水量的相對(duì)敏感度越小，α減小50%時(shí)，相對(duì)敏感度在0.07左右。河砂孔隙度n對(duì)30 cm 根區(qū)儲(chǔ)水量的影響較為顯著，n越小，相對(duì)敏感度越大，n減小50%時(shí)，其相對(duì)敏感度在0.2 左右。對(duì)于30 cm 根區(qū)含鹽量來(lái)說(shuō)，α越小，相對(duì)敏感度越高，但是總體影響較小；根據(jù)模擬結(jié)果可知，河砂孔隙度減小，30 cm 根區(qū)含鹽量反而增大，在n減小40%時(shí)，30 cm 根區(qū)含鹽量的相對(duì)敏感系數(shù)最大，在0.105 左右。說(shuō)明在上細(xì)下粗的強(qiáng)異質(zhì)層狀土的蒸發(fā)過(guò)程中，下層河砂的孔隙度對(duì)于30 cm 根區(qū)儲(chǔ)水量影響較大，對(duì)于其他結(jié)果影響較小。

3 層狀土結(jié)構(gòu)對(duì)水鹽運(yùn)移影響的情景模擬分析

在蒸發(fā)過(guò)程中，由于實(shí)測(cè)值[16]與模擬值的符合效果不佳，因此，為了更好的分析層狀結(jié)構(gòu)對(duì)蒸發(fā)過(guò)程的影響，以植物生長(zhǎng)條件下的一維土柱水鹽運(yùn)移試驗(yàn)為基礎(chǔ)[16]，利用LAWSTAC 模型對(duì)植物生長(zhǎng)條件下不同層狀土壤排列對(duì)蒸發(fā)過(guò)程中水鹽動(dòng)態(tài)的影響進(jìn)行了分析。

在情景模擬中用到兩種不同質(zhì)地的土壤，土壤參數(shù)見表1，模擬深度是50 cm，剖分為51 個(gè)節(jié)點(diǎn)，節(jié)點(diǎn)之間間距為1 cm，植物根系層厚度設(shè)置為10 cm。在不同的情景模擬中，上邊界條件采用受蒸發(fā)控制的大氣邊界。下邊界采用0 通量邊界，其他條件與以植物生長(zhǎng)條件下的室內(nèi)層狀（上層為壤土，下層為河砂）一維土柱水鹽運(yùn)移試驗(yàn)條件一致[16]。

在土柱試驗(yàn)的基礎(chǔ)上，分別設(shè)置上細(xì)下粗型和上粗下細(xì)型兩種不同排列的土壤，用LAWSTAC 模型模擬這兩種情景在蒸發(fā)條件下土壤中的水鹽狀況，并分析層狀土對(duì)蒸發(fā)量和土壤中鹽分累積的影響，圖13 和圖14 給出了情景設(shè)置的示意圖。

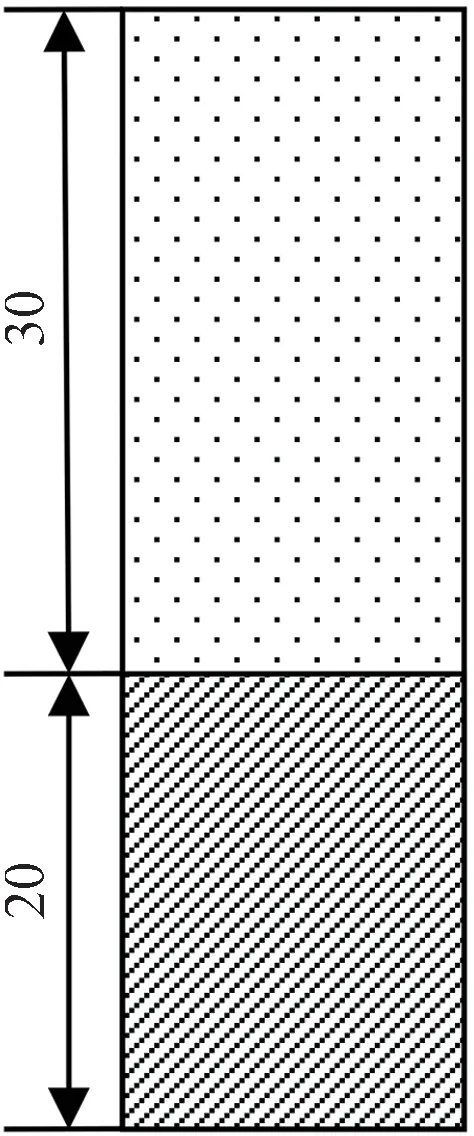
圖13 “上細(xì)下粗”型土壤情景設(shè)置示意圖（單位：cm）Fig.13 Schematic diagram of "fine on top and coarse on bottom fine" soil scenario setting

3.1 蒸散發(fā)量分析

不同排列下的蒸散發(fā)量如表6所示。上細(xì)下粗型層狀土的植物蒸騰量與土壤蒸發(fā)量的比例約為0.1，而在上粗下細(xì)型層狀土中，植物蒸騰量與土壤蒸發(fā)量相差不大。上粗下細(xì)型層狀土的植物蒸騰量要比上細(xì)下粗型層狀土的植物蒸騰量少0.002 cm，說(shuō)明上層為粗質(zhì)土是不利于植物的蒸騰的，土質(zhì)結(jié)構(gòu)的改變影響了植物的蒸騰速率。對(duì)于棵間蒸發(fā)量來(lái)說(shuō)，上粗下細(xì)型層狀土的棵間蒸發(fā)量要遠(yuǎn)遠(yuǎn)小于上細(xì)下粗型層狀土，這是由于粗質(zhì)土對(duì)下層水分運(yùn)動(dòng)有阻礙作用，這與李毅等[20,21]的研究結(jié)論一致，即粗質(zhì)土在土表時(shí)，蒸發(fā)量最小。

表6 不同排列下蒸散發(fā)量 cmTab.6 Evapotranspiration under different arrangements

3.2 土壤水分運(yùn)動(dòng)分析

不同排列下蒸發(fā)時(shí)的體積含水率模擬結(jié)果如圖15 和圖16所示，分別取上層5 cm、15 cm 和25 cm 3 個(gè)觀測(cè)點(diǎn)和下層35 cm 一個(gè)觀測(cè)點(diǎn)來(lái)分析體積含水率的變化。由圖15 可知粗質(zhì)土體積含水率低于細(xì)質(zhì)土體積含水率。上層細(xì)質(zhì)土體積含水率隨時(shí)間減小，但是減小幅度不大，蒸發(fā)進(jìn)行到100 h 左右時(shí)，上層粗質(zhì)土的體積含水率開始變化，而且下層體積含水率降低幅度要大于上層細(xì)質(zhì)土，說(shuō)明上細(xì)下粗型層狀結(jié)構(gòu)蒸發(fā)失水主要來(lái)自下層粗質(zhì)土，粗質(zhì)土位于下層時(shí)對(duì)水分運(yùn)動(dòng)的阻礙作用不明顯。

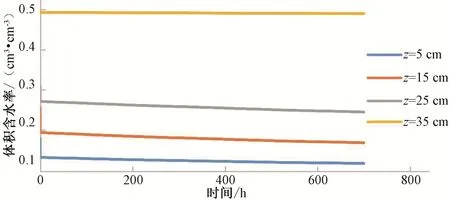
圖16 上粗下細(xì)型體積含水率模擬結(jié)果對(duì)比Fig.16 Comparison of simulation results of upper coarse and lower fine bulk moisture content

由圖16 可知下層細(xì)質(zhì)土的體積含水率基本不變，那么蒸發(fā)失水主要來(lái)自上層粗質(zhì)土，上層粗質(zhì)土在蒸發(fā)初始階段體積含水率瞬間減小，之后以較小的速率穩(wěn)定蒸發(fā)，產(chǎn)生這種現(xiàn)象主要是粗質(zhì)土的導(dǎo)水率以及孔隙度過(guò)大，由于蒸發(fā)是在各層體積含水率接近飽和的狀態(tài)下開始的，所以水分在蒸發(fā)的同時(shí)也向下運(yùn)動(dòng)，水分下滲速率遠(yuǎn)遠(yuǎn)大于蒸發(fā)速率，導(dǎo)致初始階段的體積含水率下降很快。由于下層粗質(zhì)土的級(jí)配越差，有效粒徑越大，越不利于水分的運(yùn)行，所以上層的粗質(zhì)土有阻礙水分運(yùn)動(dòng)的作用，下層細(xì)質(zhì)土蒸發(fā)失水較少，體積含水率變化不大，這與史文娟等[21-23]的研究結(jié)果一致。

對(duì)比上細(xì)下粗型層狀土和上粗下細(xì)型層狀土的體積含水率變化可知，上細(xì)下粗型層狀土體積含水率變化幅度遠(yuǎn)大于上粗下細(xì)型層狀土，即上細(xì)下粗型層狀土的累積蒸發(fā)量要遠(yuǎn)大于上粗下細(xì)型層狀土，也可以得出粗質(zhì)土位于上層起到抑制蒸發(fā)的作用，這與Huang等[21,24]人的研究結(jié)果一致。

3.3 土壤鹽分濃度的分析

不同排列下蒸發(fā)時(shí)的土壤鹽分濃度的模擬結(jié)果如圖17 和圖18 所示，分別取上層5 cm、15 cm 和25 cm 3 個(gè)觀測(cè)點(diǎn)和下層35 cm 一個(gè)觀測(cè)點(diǎn)來(lái)分析土壤鹽分濃度值的變化。由圖17可知各層的濃度是隨蒸發(fā)的進(jìn)行而增加的，鹽分隨水分向上遷移，水分蒸發(fā)之后鹽分就累積在各層土中，所以鹽分濃度升高，下層粗質(zhì)土并未對(duì)鹽分的運(yùn)移產(chǎn)生抑制作用。由圖18可知15 cm 和25 cm 上層鹽分濃度逐漸減小，由于粗質(zhì)土層對(duì)鹽分的吸附作用較小，鹽分無(wú)法在層間停留，導(dǎo)致鹽分濃度隨后降低，鹽分濃度的降低可以有效降低根系層內(nèi)的含鹽量，減小植物的鹽分脅迫。5 cm 土層鹽分濃度前期有上升趨勢(shì)是由于上層植物根系的阻滯作用，增加了根系層內(nèi)的鹽分。下層細(xì)質(zhì)土蒸發(fā)初期隨蒸發(fā)的進(jìn)行鹽分會(huì)向上累積，后期土壤的鹽分濃度趨于穩(wěn)定，上層粗質(zhì)土對(duì)鹽分遷移有一定的阻礙作用，鹽分遷移受到抑制，最終鹽分累積在交界面處，這與鄒桂梅[25]等研究夾砂土有阻隔鹽分的結(jié)果一致。

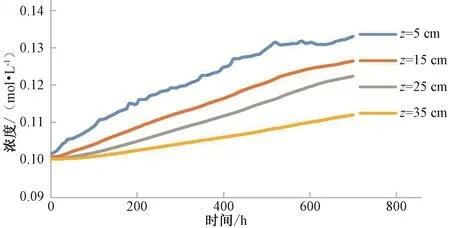
圖17 上細(xì)下粗型土壤鹽分濃度模擬結(jié)果對(duì)比Fig.17 Comparison of simulation results of salt concentration in fine and coarse soils

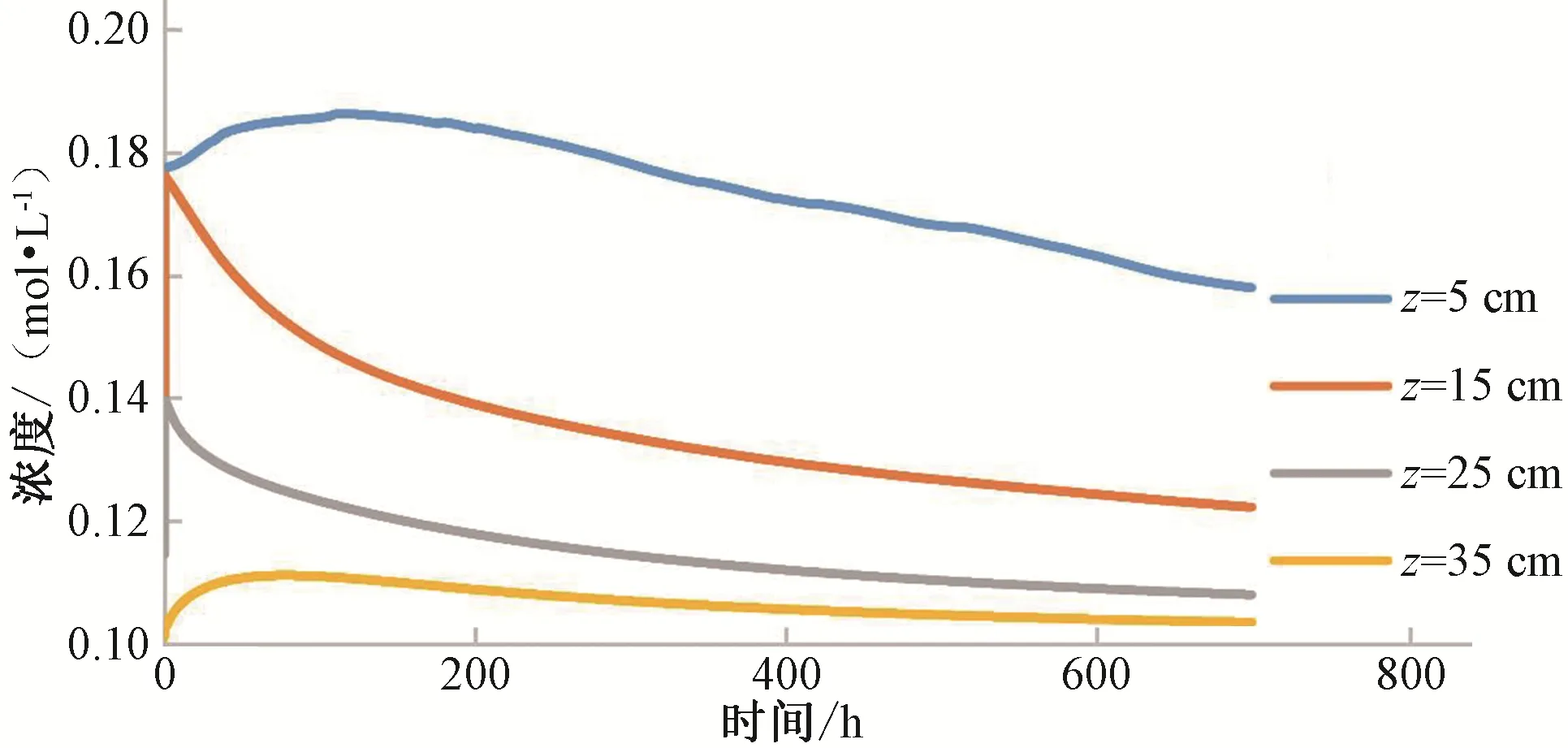
圖18 上粗下細(xì)型土壤鹽分濃度模擬結(jié)果對(duì)比Fig.18 Comparison of simulation results of salt concentration in coarse and fine soils

4 結(jié) 論

在植物生長(zhǎng)條件下的一維土柱水鹽運(yùn)移試驗(yàn)的基礎(chǔ)上[16]，利用Matlab 軟件的LAWSTAC 模型分別模擬均質(zhì)土柱和層狀土柱中的水鹽運(yùn)移全過(guò)程，得到以下結(jié)論：

（1）如果LAWSTAC 模型選擇的壤土的水力特性參數(shù)合理，那么LAWSTAC 模型可以較好的模擬植被生長(zhǎng)條件下的均質(zhì)土柱在入滲及蒸發(fā)條件下的水鹽運(yùn)移過(guò)程。

（2）對(duì)于有植被生長(zhǎng)上細(xì)下粗型強(qiáng)異質(zhì)層狀土來(lái)說(shuō)，LAWSTAC 模型可以較好的模擬入滲條件下的層狀土水鹽運(yùn)移情況，但是對(duì)于蒸發(fā)過(guò)程來(lái)說(shuō)，由于下層河砂參數(shù)選取的誤差亦或由于目前水鹽運(yùn)移理論在有優(yōu)先流存在的層狀土中適用性不好，導(dǎo)致模型模擬蒸發(fā)過(guò)程的效果不佳。

（3）對(duì)蒸發(fā)過(guò)程中層狀土下層河砂的基本水力特性參數(shù)α和n進(jìn)行單因素敏感性分析，結(jié)果發(fā)現(xiàn)參數(shù)n對(duì)于植物蒸騰量、根區(qū)儲(chǔ)水量及含鹽量的影響程度大于參數(shù)α。

（4）應(yīng)用LAWSTAC 模型分析在蒸發(fā)條件下不同土壤排列(上粗下細(xì)、上細(xì)下粗)對(duì)土壤中的水鹽動(dòng)態(tài)以及蒸散發(fā)量的影響中得出：粗質(zhì)土覆蓋細(xì)質(zhì)土能有效減小蒸發(fā)量及蒸騰量，上層粗質(zhì)土對(duì)水分運(yùn)動(dòng)和鹽分運(yùn)移均有抑制作用。上粗下細(xì)型層狀結(jié)構(gòu)土壤的蒸發(fā)失水主要來(lái)自上層粗質(zhì)土；而上細(xì)下粗型層狀結(jié)構(gòu)土壤的蒸發(fā)失水主要來(lái)自下層粗質(zhì)土，且其累積蒸發(fā)量遠(yuǎn)大于上粗下細(xì)型層狀土。

本文選取的下層粗質(zhì)土過(guò)粗，這種情況易出現(xiàn)優(yōu)先流，水流和溶質(zhì)運(yùn)移出現(xiàn)較大空間變異，給試驗(yàn)觀測(cè)、結(jié)果分析以及數(shù)值模擬帶來(lái)較大困難，這也為優(yōu)先流理論的發(fā)展提出了挑戰(zhàn)。

由于實(shí)測(cè)值試驗(yàn)選取的植物是特定水生植物，且不夠耐旱耐鹽，蒸發(fā)進(jìn)行到一定程度時(shí)，植物出現(xiàn)凋萎現(xiàn)象。同時(shí)受測(cè)試儀器的工作原理所限，本文中層狀土中的土壤體積含水率和鹽分濃度實(shí)測(cè)值是土壤中某個(gè)深度范圍的平均值。在土壤水鹽分布具有較大空間變異的情況下（例如發(fā)生指流、層狀土壤交界面處），土壤中水分及鹽分的變化還需要更精細(xì)的監(jiān)測(cè)。另外，本研究中層狀土中鹽分的監(jiān)測(cè)是通過(guò)監(jiān)測(cè)土壤溶液中電導(dǎo)率的變化，再利用標(biāo)定曲線轉(zhuǎn)化為鹽分濃度的，當(dāng)土壤鹽分濃度較高或者產(chǎn)生結(jié)晶情況下，測(cè)量誤差較大，這些為模型模擬帶來(lái)困難。同時(shí)為精密介入式測(cè)量?jī)x器的研制提出了挑戰(zhàn)。

文章建立的植物生長(zhǎng)條件下的層狀土水鹽運(yùn)移的LAWSTAC 模型，在模擬下層粗質(zhì)土較粗情況時(shí)，由于參數(shù)設(shè)置的導(dǎo)水率偏大以及實(shí)際情況中出現(xiàn)優(yōu)先流，導(dǎo)致模型模擬情況不佳，可以在模型設(shè)置與程序計(jì)算方法上進(jìn)行改進(jìn)。