結(jié)構(gòu)鋼試件不同載荷下斷鉛聲發(fā)射信號的混沌特征＊

劉婷，張堃，郭曉艷

（中山火炬職業(yè)技術(shù)學(xué)院，廣東 中山 528437）

Q235 鋼是一種碳素結(jié)構(gòu)鋼，由于它含碳適中，綜合性能較好，因此無論是在建筑、工程結(jié)構(gòu)中，還是在機(jī)械零件中，Q235 鋼都有很大的需求體量。也正因Q235 鋼應(yīng)用的廣泛性，在實際的工程應(yīng)用中，對Q235鋼內(nèi)部損傷程度進(jìn)行無損檢測，無論在事故預(yù)防，還是在舊零件再制造等方面都具有極其重要的意義[1]。現(xiàn)在常用的無損檢測方法有很多，如超聲檢測、電磁監(jiān)測、聲發(fā)射檢測、紅外檢測等，而在諸多無損檢測方法中，聲發(fā)射檢測技術(shù)因其靈敏度高、抗干擾能力強(qiáng)等優(yōu)點(diǎn)，日益成為無損檢測方面的研究熱點(diǎn)[2]。

張穎等[3]對由Q235 鋼可視化原位拉伸實驗所獲取的聲發(fā)射源信號進(jìn)行了分析，根據(jù)聲發(fā)射源動態(tài)觀察結(jié)果及圖像分析，建立了Q235 的聲發(fā)射細(xì)觀損傷模型；陳冰等[4]通過時頻特征分析在聲發(fā)射信號中提取帶鋸條全生命周期的磨損信號特征，判斷帶鋸條的初始劇烈磨損時間；毛漢穎等[5]通過斷鉛聲發(fā)射信號，估算金屬材料的聲阻抗值，表征了金屬材料的損傷程度；賀秀麗等[6]利用聲發(fā)射技術(shù)對鎂合金進(jìn)行監(jiān)測，分析了在腐蝕及疲勞載荷等不同情況下的聲發(fā)射波形特征；綦磊等[7]以聲發(fā)射技術(shù)為基礎(chǔ)，采用混沌-BP 神經(jīng)網(wǎng)絡(luò)相結(jié)合的方法，實現(xiàn)了泄漏檢測及對漏孔大小的評估。

為了有效分析Q235 鋼金屬材料內(nèi)部損傷程度，基于金屬材料損傷非線性的特點(diǎn)，本文首先對不同損傷情況的Q235 鋼進(jìn)行斷鉛聲發(fā)射試驗，激勵其內(nèi)部損傷特征，獲取斷鉛聲發(fā)射信號；然后采用混沌分形理論對獲得的斷鉛聲發(fā)射信號進(jìn)行特征分析，通過計算不同損傷程度下的結(jié)構(gòu)鋼的聲發(fā)射信號的關(guān)聯(lián)維數(shù)、最大Lyapunov 指數(shù)及Kolmogorov 熵值，進(jìn)行綜合比較，以期檢測出聲發(fā)射信號中的損傷信息，從而實現(xiàn)對金屬材料內(nèi)部損傷程度的判斷。

1 斷鉛聲發(fā)射試驗設(shè)置

試件采用尺寸為210 mm×30 mm×1 mm 的Q235鋼材料，為了模擬損傷狀態(tài)，對所有鋼材進(jìn)行拉伸試驗，最大拉力分別設(shè)為0 kN、4 kN、8 kN、12 kN、14 kN。受到5 種不同級別的最大拉力的試件，分別用于模擬5 種不同損傷程度的損傷試件。

本試驗平臺采用美國物理聲學(xué)公司（PAC）生產(chǎn)的PCI-II系統(tǒng)進(jìn)行斷鉛試驗：在試件的一端放置傳感器，試件另一端設(shè)置斷鉛點(diǎn)，位置如圖1 所示。試驗中，使用HB 鉛筆，保證其與試件表面成30°夾角，均勻用力壓斷鉛芯，采集產(chǎn)生的聲發(fā)射信號。

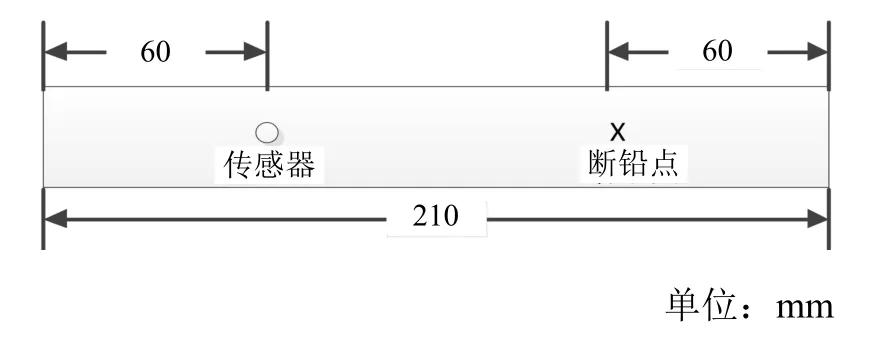
圖1 試件示意圖

分別對先前制備的5 種不同損傷程度的試件進(jìn)行斷鉛試驗，斷鉛產(chǎn)生的聲發(fā)射信號沿試件傳遞，經(jīng)過損傷部位后被傳感器接收，記錄聲發(fā)射信號數(shù)據(jù)。為減少誤差，對每組試件分別進(jìn)行5 次試驗后，取獲得的數(shù)據(jù)的平均值進(jìn)行后續(xù)分析。

2 混沌特征量算法

2.1 關(guān)聯(lián)維數(shù)

在機(jī)械故障診斷中，經(jīng)常用關(guān)聯(lián)維數(shù)[8-10]來定量說明系統(tǒng)的復(fù)雜程度，這是機(jī)械故障診斷中一種重要的方法。

關(guān)聯(lián)維數(shù)有多種計算方法，本文采用G-P 算法進(jìn)行計算：首先對原始時間序列進(jìn)行相空間重構(gòu)，取該相空間中的一個相點(diǎn)為中心，計算相點(diǎn)落入超球體之內(nèi)的概率，即關(guān)聯(lián)積分為：

式中：m為相空間重構(gòu)中的嵌入維數(shù)的數(shù)值；N（m）為重構(gòu)向量的個數(shù)；r為超球體半徑的數(shù)值；H為Heaviside 函數(shù)。

Heaviside 函數(shù)的公式為：

將r適當(dāng)縮小，根據(jù)關(guān)聯(lián)積分與r的關(guān)系式，可得：

式中：d為關(guān)聯(lián)維數(shù)的數(shù)值。

關(guān)聯(lián)維數(shù)d的公式為：

如果關(guān)聯(lián)維數(shù)隨著嵌入維數(shù)m的增加而不斷增加，則表示數(shù)據(jù)為隨機(jī)序列；如果關(guān)聯(lián)維數(shù)隨著嵌入維數(shù)m的增加而增加，最后無限趨于飽和，則表示為混沌序列。

根據(jù)G-P 法獲得關(guān)聯(lián)維數(shù)的計算結(jié)果，如圖2 所示。首先對lnC（r）-lnr曲線（如圖2（a）所示）中的直線段部分進(jìn)行最小二乘擬合，即可求得每條直線段的斜率，結(jié)果如圖2（b）所示。關(guān)聯(lián)維數(shù)d即斜率隨m的增加而趨向飽和的那個值。

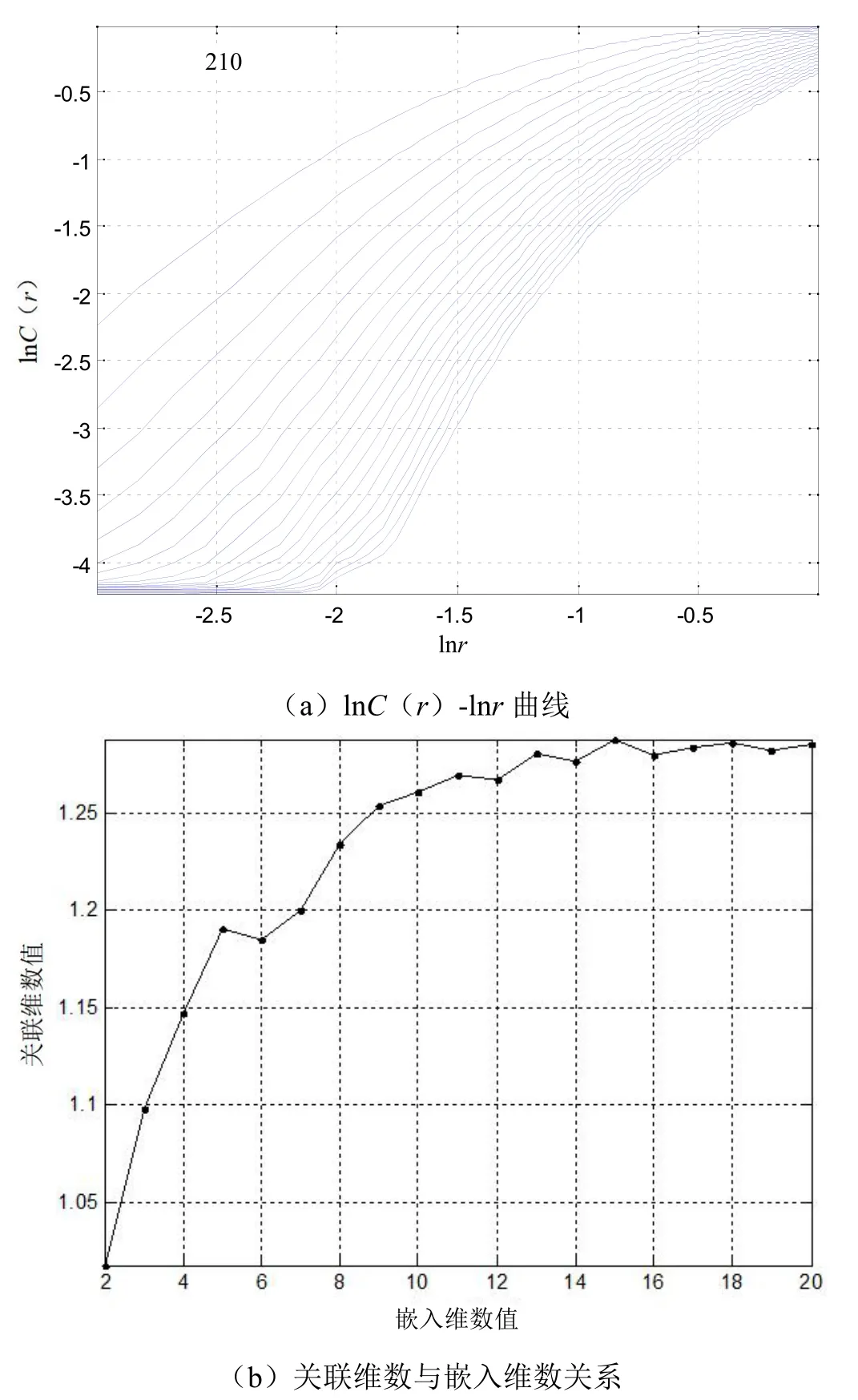
圖2 關(guān)聯(lián)維數(shù)計算過程

從圖2（b）的曲線中可以看出，一開始，斜率隨m的增加而增加，當(dāng)m增加到14 之后，斜率變化變成在一定的區(qū)間內(nèi)波動，并且逐漸平穩(wěn)，趨于飽和。此時，對平穩(wěn)區(qū)間內(nèi)的斜率取平均值，即得到時間序列的關(guān)聯(lián)維數(shù)為1.28。

同理，可以計算得到其他不同損傷程度的試件的信號的關(guān)聯(lián)維數(shù)值，從而得到不同損傷程度下的試件的聲發(fā)射信號的關(guān)聯(lián)維數(shù)的變化趨勢，如圖3 所示。

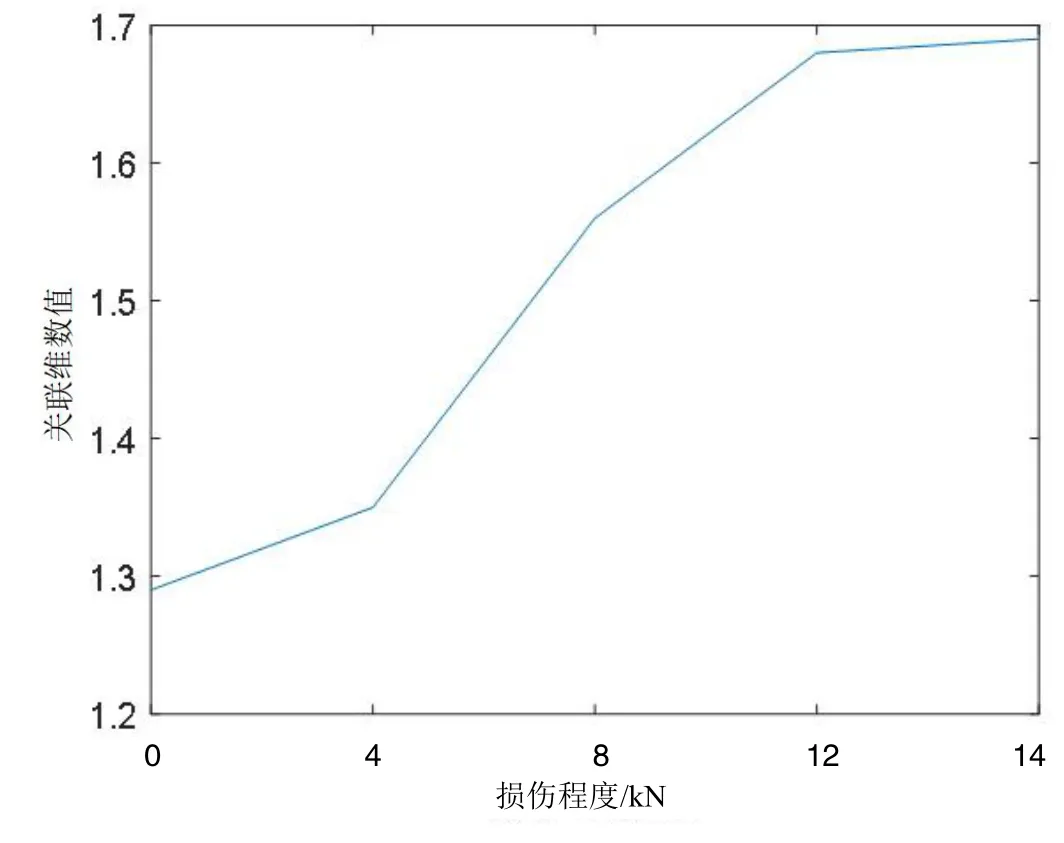
圖3 不同損傷程度下的關(guān)聯(lián)維數(shù)值

2.2 最大Lyapunov 指數(shù)

Lyapunov 指數(shù)是相鄰相空間軌道按指數(shù)發(fā)散或收斂的速度的一種定量描述，本文采用小數(shù)據(jù)量法計算各損傷程度下時間序列的最大Lyapunov 指數(shù)值λ1[11-12]。首先在重構(gòu)的相空間中計算第j個參考點(diǎn)Xj與最近相鄰點(diǎn)Xj?之間的初始距離dj（0），即：

式中：p為時間序列的平均周期的數(shù)值。

計算出各參考點(diǎn)Xj與最近相鄰點(diǎn)Xj?的第i個離散時間步長后的距離dj（i），即：

這里假設(shè)參考點(diǎn)Xj與最近相鄰點(diǎn)Xj?具有λ1的指數(shù)發(fā)散率，根據(jù)上式計算可得到：

利用最小二乘法擬合y（i）曲線中的線性區(qū)域即可得到最大Lyapunov 指數(shù)值λ1。如果最大Lyapunov指數(shù)值大于0，則判定系統(tǒng)混沌，并且最大Lyapunov指數(shù)值越大，系統(tǒng)越混沌。

以無損條件下試件為例，其最大Lyapunov 指數(shù)值的計算過程如圖4 所示。根據(jù)小數(shù)據(jù)量法，用最小二乘法對y（i）曲線的線性部分進(jìn)行擬合，得到的斜率就是此時的最大Lyapunov 指數(shù)值，為0.012 4。同理，可以得到其他幾種不同損傷程度下試件的聲發(fā)射信號的最大Lyapunov 指數(shù)值，其變化趨勢如圖5 所示。

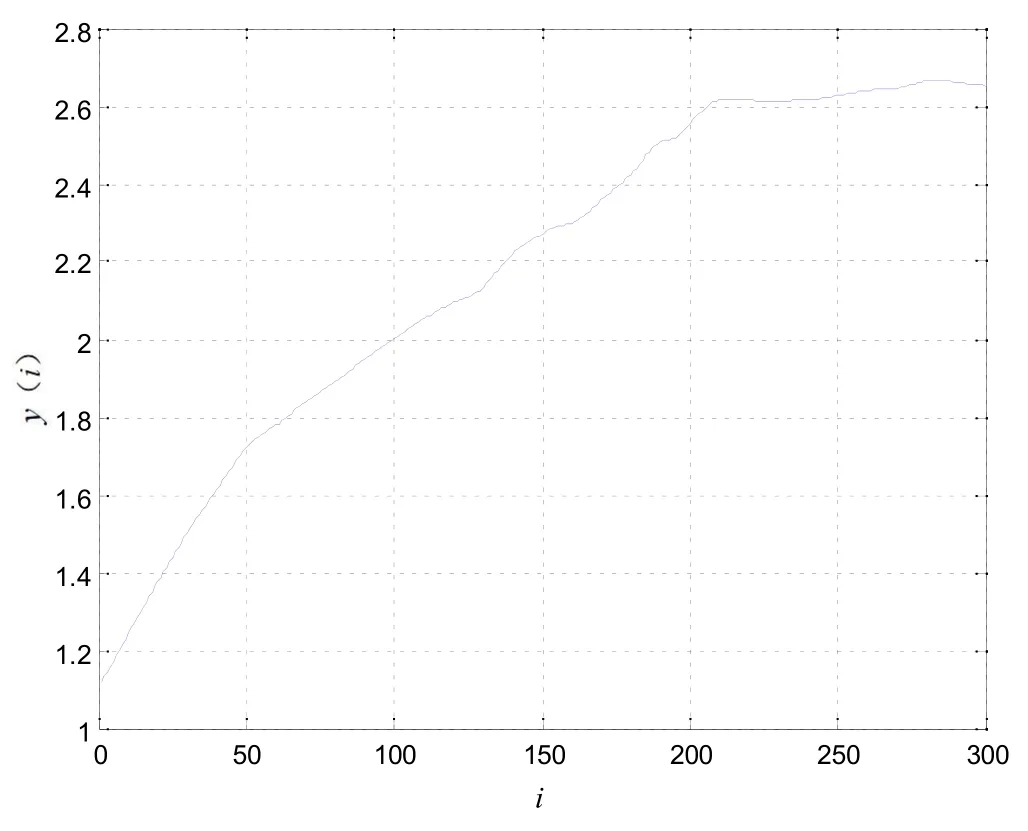
圖4 最大Lyapunov 指數(shù)值的計算過程

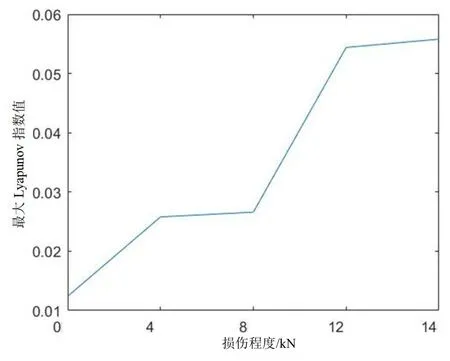
圖5 不同損傷程度下的最大Lyapunov 指數(shù)值

2.3 Kolmogorov 熵

Kolmogorov 熵（以下簡稱“K 熵”）是表達(dá)混沌系統(tǒng)的一個非常重要的量，它反映了系統(tǒng)的混亂度，其數(shù)值根據(jù)不同類型的動力學(xué)系統(tǒng)而不同：若K 熵的值為0，則系統(tǒng)為規(guī)則系統(tǒng)；若K 熵的值是無界的，則系統(tǒng)為隨機(jī)系統(tǒng)；若K 熵的值大于0 且有限，則系統(tǒng)為混沌運(yùn)動系統(tǒng)，并且K 熵值越大，信息損失速率越大，系統(tǒng)的混沌程度越高[13]。

本文根據(jù)最大似然法計算各組不同損傷程度下試件的聲發(fā)射信號的K 熵，得到的結(jié)果如圖6 所示。

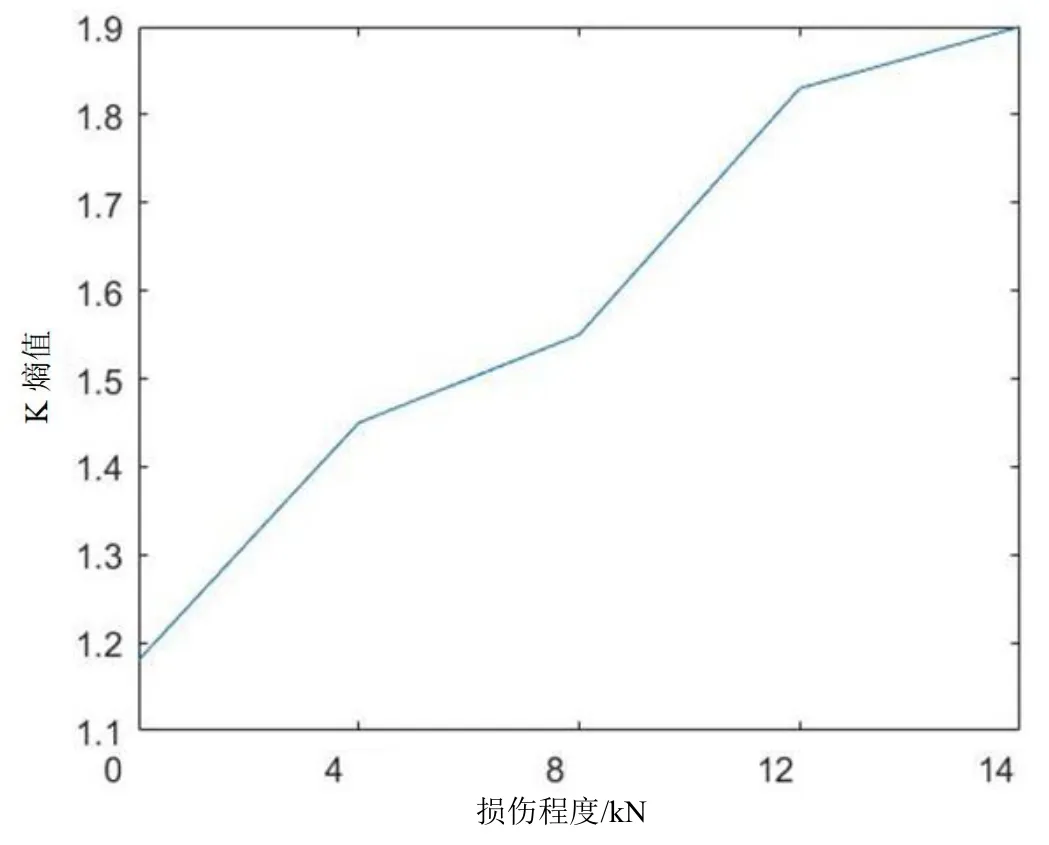
圖6 不同損傷程度下的K 熵值

3 斷鉛聲發(fā)射信號的混沌特征分析

由上述計算結(jié)果顯示，采集到的不同損傷程度的試件的聲發(fā)射信號時間序列均具有正的最大Lyapunov指數(shù)，并且關(guān)聯(lián)維數(shù)都能夠達(dá)到飽和狀態(tài)，表明采集得到的聲發(fā)射信號時間序列具有混沌特征。

為了便于分析，將上述計算得到的3 種混沌特征量的值進(jìn)行歸一化處理，并繪制趨勢圖，如圖7 所示。

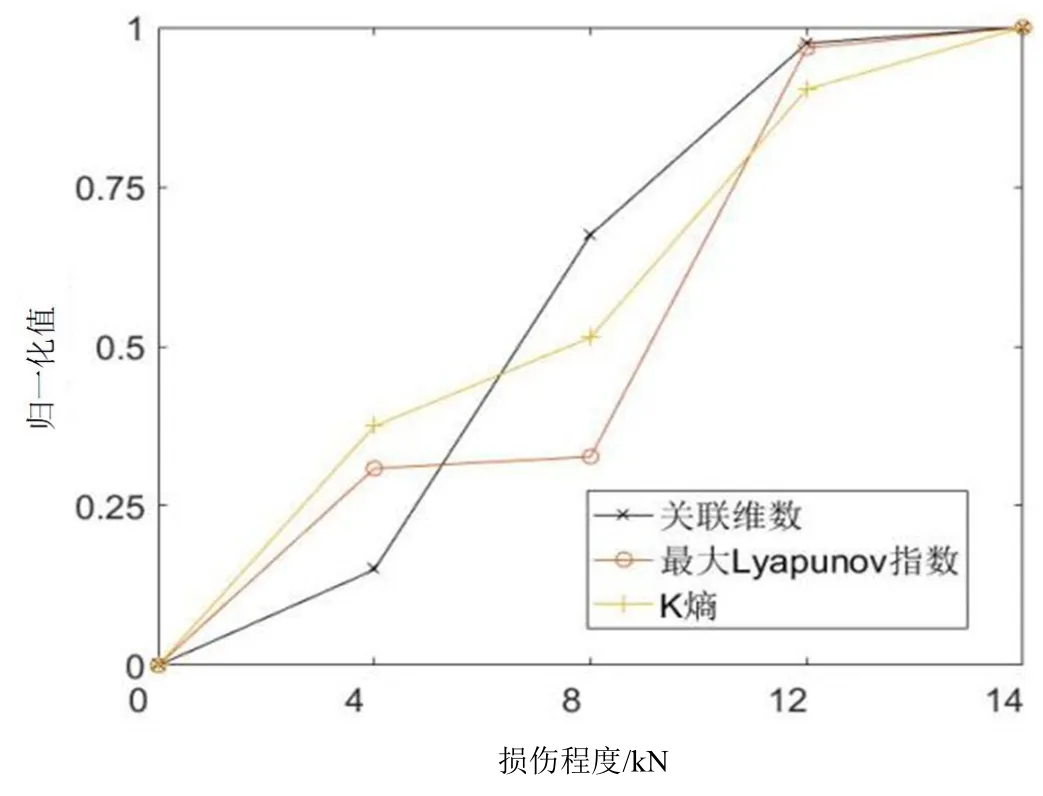
圖7 歸一化特征值

從圖中可以看到，隨著試件損傷程度的增加，3種混沌特征值都呈上升趨勢，不難分析，隨著試件所受拉力的增加，試件的損傷程度不斷增大，大量的微裂紋開始發(fā)生萌生，并且不斷擴(kuò)展，導(dǎo)致試件的非線性程度不斷增加，所以混沌特征值也隨之不斷上升。

同時可以發(fā)現(xiàn)，在模擬試件損傷前期（所受拉力為0～8 kN 時），關(guān)聯(lián)維數(shù)的增幅相較其他2 種混沌特征值更明顯。分析可知，此時的試件處于拉伸變形的彈性變形階段，微裂紋開始萌生，試件內(nèi)部復(fù)雜程度高，而關(guān)聯(lián)維數(shù)正好能夠很好地描述系統(tǒng)的復(fù)雜程度，因此該值的增幅程度相對較大；在模擬試件損傷中后期（所受拉力為8～12 kN 時），試件處于拉伸曲線由屈服階段到塑性變形階段的過程中，分布不均的微裂紋大量萌生和擴(kuò)展，此時可以發(fā)現(xiàn)最大Lyapunov指數(shù)的增幅更大，說明Lyapunov 指數(shù)對金屬材料內(nèi)部損傷的發(fā)展階段更加敏感；在模擬試件損傷后期（所受拉力為12～14 kN 時），試件到達(dá)塑性變形階段，發(fā)生形變并趨于斷裂，此時內(nèi)部裂紋擴(kuò)展大小方向趨于統(tǒng)一，混沌特征量也趨于飽和，其變化幅度不再像受損傷前中期那樣劇烈，而是逐漸趨于平穩(wěn)。

4 結(jié)束語

為了實現(xiàn)對金屬損傷程度的判定，本文通過利用Q235 鋼進(jìn)行聲發(fā)射斷鉛試驗，激勵對其內(nèi)部損傷進(jìn)行混沌特征量分析，得到以下結(jié)果：①試驗結(jié)果表明，隨著試件損傷程度的增大，混沌特征值也增大。因此，通過聲發(fā)射信號計算得到的關(guān)聯(lián)維數(shù)、最大Lyapunov指數(shù)、K 熵的值與結(jié)構(gòu)鋼試件的損傷程度呈正相關(guān)關(guān)系，這3 種混沌特征值反映了結(jié)構(gòu)鋼試件內(nèi)部的復(fù)雜性和無序性，其變化趨勢能夠在一定程度上對金屬材料損傷程度進(jìn)行表征。②不同損傷程度下試件的聲發(fā)射信號所對應(yīng)的混沌特征值敏感程度不同。不難發(fā)現(xiàn)，試驗結(jié)果中計算得到的關(guān)聯(lián)維數(shù)對結(jié)構(gòu)鋼試件內(nèi)部發(fā)生損傷的萌生階段更敏感，而在結(jié)構(gòu)鋼試件內(nèi)部損傷的發(fā)展階段，最大Lyapunov 指數(shù)的增量更明顯，因此，不同損傷階段的結(jié)構(gòu)鋼利用不同的混沌特征值能夠更好地實現(xiàn)損傷程度判定。③通過試驗證明，斷鉛聲發(fā)射信號能夠激勵結(jié)構(gòu)鋼內(nèi)部的損傷信息，并且結(jié)合結(jié)構(gòu)鋼聲發(fā)射信號的多個混沌特征值，可以從不同角度來實現(xiàn)對結(jié)構(gòu)鋼損傷程度的共同判定，為金屬損傷程度判斷奠定了基礎(chǔ)，并且為金屬損傷識別的應(yīng)用方面提供了一定的試驗依據(jù)。