基于梯度提升決策樹的鍋爐燃燒優(yōu)化控制策略研究

肖 勇，馬 樂，胡 波，王藝晴，毛 華

（西安熱工研究院有限公司，陜西西安 710054）

鍋爐燃燒控制系統的合理管控，對于提高燃燒效率、減少污染物排放及降低成本具有重要意義[1-3]。其中，超超臨界的鍋爐燃燒調整需要基于風煤比、煤水比與功煤比進行。但由于超超臨界鍋爐受到多種因素的影響，故其具有強耦合度及高非線性的特點，需要進行大量的反饋校正與基于經驗的調整。換言之，只有當系統出現問題時才會進行校正，極大地降低了效率，并有可能影響調整效果。此外，若校正設置不合理，還會帶來相反的結果，影響鍋爐及周邊設備的安全運行。因此，開展超超臨界鍋爐燃燒的最優(yōu)化控制研究至關重要。

文中針對超超臨界鍋爐的最優(yōu)化控制問題，引入了梯度提升決策樹（Gradient Boosting Decision Tree，GBDT）技術，同時基于燃燒粒子模型建立了相關算法，并通過實驗進行了驗證。

1 鍋爐燃燒模型

該研究中的鍋爐模型由一組偏微分方程構成[4]，這些方程描述了氣態(tài)流體在反應爐中的時間及空間運動。此外，還使用了非均質模型，用于預測氣固相之間的邊界層厚度等重要屬性。

該文設計的鍋爐燃燒模型考慮的假設如下：

1）反應粒子被建模為完美的球形粒子；

2）反應粒子具有恒定的體積；

3）反應粒子顆粒具有宏觀上均勻的結構，且不受反應的影響；

4）反應粒子顆粒內金屬氧化物分布均勻；

5）反應器內的反應粒子分布均勻。

圖1 為反應爐示意圖，其說明了反應器模型與反應粒子模型在邊界條件下的相互作用。在此基礎上，建立反應器和反應粒子的質量及熱平衡方程。

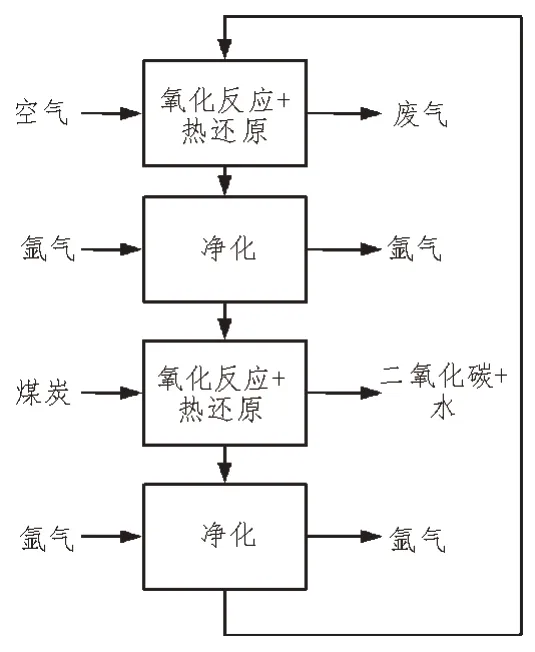
圖1 反應器示意圖

填充床反應器的質量和能量平衡公式如下：

式中，Ci,j為階段j的初始濃度，Fi,j為氣體種類的摩爾流量，Daxi,j為第j階段物種i的軸向色散系數，x和z表示反應器的兩個方向，t為時間，V為流速。εb、Ac、kci,j和av為對應標量參數，Tcj和Tj分別表示入口及反應中的溫度[5]。同樣，體相的邊界條件如下：

式中，yifeedj為進料中第i種物質的摩爾分數，Finj為入口處氣體種類i的摩爾流量，Ac為直管截面積，Cpjj為反應粒子在階段j的熱容量，ρin,j為j階段氣體混合物的熱導率，εb和λaxj是對應的標量參數。

在反應器的質量與能量平衡方程中，軸向位置由z(0≤z≤L)表示，L為反應器的長度。類似地，時間變化表示為t(0≤t≤tj,final)，其中tj,final表示反應中每個階段j的批處理時間。此外，Tj(z,t)表示反應過程中每個階段在空間及時間域上的溫度分布。式（1）-（2）明確考慮了反應器體相與位于反應器中軸向位置z的反應粒子顆粒間的對流、軸向擴散、質量和熱傳遞；式（3）-（4）表述的邊界條件，分別描述了反應器入口處的質量和熱量進料流條件；式（5）則描述了反應器出口流的質量與隔熱條件，而方程式（6）描述了每個階段j的入口質量通量。

反應粒子的質量和能量平衡公式如下：

粒子相所需的邊界條件如下：

式中，粒子的徑向位置由rc(0≤rc≤Rp)表示；Rp表示粒子的半徑；Ci,j(z,r,t)表示粒子徑向和時間域中在每個階段j時氣體種類i的濃度，而Tcj(z,r,t)則表示反應過程中每個階段j的粒子溫度曲線。式（7）-（8）所示的粒子模型明確考慮了徑向擴散。式（9）則描述了反應粒子中心的質量及隔熱條件，并在此基礎上使用方程（7）-（8）中的Ri,j描述反應過程的動力學項。

2 基于梯度決策樹的優(yōu)化控制

該文在建立了鍋爐燃燒反應模型的基礎上，使用梯度提升決策樹研究鍋爐燃燒的優(yōu)化策略[6]。其中，XGBoosting（Extreme Gradient Boosting）是最常用的梯度決策樹算法之一。當決策樹在此過程中生長時，XGBoosting 通過計算方差增益來執(zhí)行拆分[7]。例如，令O為決策樹固定節(jié)點上的訓練集，則該節(jié)點在節(jié)點d處分裂特征j的方差增益可表示為：

對于特征j，梯度決策樹算法選擇=arg maxdVj(d)并計算最大增益[8-9]。然后根據特征j?在點dj處將數據拆分為左右子節(jié)點。大多數梯度決策樹學習算法如該文使用的XGBoosting 均是按層次生長樹，這意味著在每個集成時間步長，最深層次的所有節(jié)點均會增長。

LightGBM（Light Gradient Boosting Machine）是微軟開發(fā)的開源梯度提升決策算法軟件[10-11]。其使用基于直方圖的算法來加快訓練過程、減少內存消耗，同時結合先進的網絡通信來優(yōu)化并行學習，故被稱為并行梯度決策算法。該算法使用逐葉策略進行樹的生長，并找到具有最大方差增益的葉子進行分割。此外，還可通過計算變化增益的方式將其與其他梯度決策模型加以區(qū)分。在LightGBM 中，考慮到弱學習器與強學習器的區(qū)別，根據子集估計方差的最大增益對實例進行分割。

2.1 數據處理

若數據出現缺失，則所用算法的表現可能不佳，因此需要對數據加以處理，即數據清洗[12-14]。文中數據處理根據以下規(guī)則對所有數據集中的缺失值進行替換：若缺失觀測值的數量少于該特征實例總數的5%，則刪除這些觀測值；而在其余情況下，缺失值將替換為相應特征的眾數；此外，還對可能的異常值進行了分析。

數據處理的第二階段是將分類特征轉換為數值，以便于后續(xù)處理。

2.2 模型訓練

為了對測試集進行預測，LightGBM 訓練過程中使用的主要參數為葉子數、葉子中的最小數據量與線程數，目標是通過梯度決策樹算法使數據回歸。同時采用分層隨機抽樣方法（Stratified Random Sampling）將已處理過的數據集劃分為更小的組[15]，且該方法的分層是根據相似的屬性或特征形成的。此外，在LightGBM 中有必要為執(zhí)行的所有訓練定義層數。通過使用分層隨機抽樣方法，可以提供更多的子集來訓練模型，進而使模型表現更優(yōu)。

2.3 評價標準建立

在所有可能的模型評估指標中，均方根誤差（RMSE）沒有物理單位，其可用于衡量LightGBM 和XGboosting 預測值之間的差異。故該文選用RMSE跟蹤預測誤差的大小并衡量模型的執(zhí)行情況[16]。RMSE 是對預測值與實際值的差的平方求均值后的平方根，計算公式為：

式中，n是觀察次數，yj是預測值，是實際值。

3 實驗驗證

首先對梯度提升決策樹算法部署進行實驗驗證，將迭代次數固定為1 000 次，并計算了時間與RMSE 等輸出度量，具體如圖2 所示，其中RMSE 為虛線上每個點的標簽。觀察圖2 可知，對于較小的學習率，當時間最大時訓練精度的表征RMSE 并不是最優(yōu)的。而隨著學習率的增加，處理時間逐漸減少，但RMSE 值的變化并未出現明顯差異。因此，在將該算法用于鍋爐的最優(yōu)控制策略時，需要在訓練時間成本與準確性之間做取舍。

圖2 時間、RMSE與學習率的關系曲線

為了對選擇部署的模型進行說明，該文對兩種梯度提升決策樹技術的部署算法LightGBM 和XGBoosting 進行了驗證，以證明LightGBM 作為梯度提升決策樹組合模型的性能更優(yōu)。因此，為這兩種情況設置了相同的參數集及固定的學習率、迭代次數等信息。測量二者的RMSE，結果如圖3 所示。從圖中可以發(fā)現，LightGBM 在使用的所有學習率間隔中均比XGBoosting 表現更優(yōu)，由此表明了LightGBM更適用于設計鍋爐燃燒的優(yōu)化控制策略。

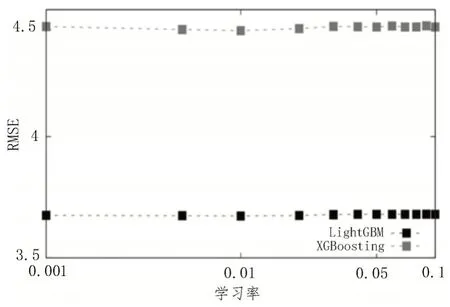
圖3 LightGBM和XGBoosting性能對比實驗

此外，為了驗證文中基于梯度提升決策樹的鍋爐燃燒最優(yōu)控制策略的優(yōu)越性，還設計了兩種情形。表1 為兩種情形的具體參數，包括各種初始條件。實驗1 相比于基本實驗情況，入口溫度更高，故其出口溫度也會較高。這便需要在控制反應物流通量的基礎上，對反應爐的壓力與溫度加以控制，因而也對燃燒控制算法提出了更加嚴苛的要求。而實驗2 所代表的情形中，在提高了壓力的基礎上降低了入口溫度，因此控制算法將重點改變反應物的流通速率。

表1 優(yōu)化實驗參數

優(yōu)化控制策略增加前后的對比實驗如圖4 所示。由圖可知，實驗1 有更長的熱回收過程，即出口氣體溫度保持額外的時間約為300 s；實驗2 的輸出能量隨著過程的發(fā)展而逐漸降低。通過積分運算可知，優(yōu)化前的基本情景能夠產生36.6 MW·h 能量，實驗1 產生45.9 MW·h 能量，增加了26%的產能；實驗2產生了43.2 MW·h 能量，增加了18%的產能。

圖4 優(yōu)化控制策略增加前后的對比實驗

4 結束語

為了提高燃燒效率，文中對具體燃燒的情況進行了分析，并建立了燃燒粒子的鍋爐燃燒模型，實現了對于氣態(tài)流體在反應爐中時空運動的準確描述，從而為控制策略的設計提供準確的系統模型。但由于燃燒粒子模型數據量較大，傳統的單輸入輸出控制算法難以進行準確控制，因此該文引入梯度提升決策樹技術，研究了大量數據情況下鍋爐燃燒的最優(yōu)化控制策略。通過實驗，對算法的部署及控制算法的有效性進行了探索。

鍋爐模型建模的復雜程度，會進一步決定優(yōu)化策略的有效性。此外，使用傳感器網絡進行控制反饋，對于控制精度的提升也具有重要意義。因此，該研究的下一步工作將在有限計算資源的情況下進行，以提高建模的精度，并建立高效、準確的傳感器網絡，從而實現更為環(huán)保的鍋爐燃燒控制算法。