輪式機器人雙環軌跡物聯網安全傳感控制技術

蔡 娜，劉 磊

（北京計算機技術及應用研究所，北京 100854）

軌跡控制技術[1-3]是機器人完成指令與任務的基礎與關鍵，只有高精度控制，才能保證機器人在復雜環境中的工作效率。為取得理想的機器人軌跡控制效果，相關領域研究人員從不同角度展開了深入探索。如文獻[4-6]分別采用機器視覺技術、變增益自抗擾技術、Udwadia-Kalaba 理論，提出有效且可行的軌跡控制方法。

機器人是物聯網技術的移動終端，兩者關系密切，且適配度較高。輪式機器人[7]作為移動類機器人的主要代表，機械結構簡單，機動性與靈活性較大，應用范圍最廣。文中基于上述特征，在物聯網中嵌入安全傳感節點，結合雙環控制技術與輸出調節自動控制技術，設計出輪式機器人的運動軌跡控制技術。

1 輪式機器人運動軌跡物聯網安全傳感定位

1.1 物聯網安全傳感架構

1.1.1 物聯網網絡

針對輪式機器人的大部分工作環境，采用感知層、網絡層、應用層三個部分，構建物聯網網絡結構，各部分之間通過高分辨率無線信道相連[8]。該網絡架構中各部分的技術支持與具體功能如表1 所示。

表1 物聯網網絡各層級功能

1.1.2 安全傳感節點

在物聯網感知層中，存在三種傳感節點，即終端感知節點、數據集成節點、數據管理節點。采用Zigbee技術[9]動態添加傳感節點至無線傳感網絡，通過射頻遙控技術實現該節點與服務器之間的無線通信。安全傳感節點架構如圖1 所示。

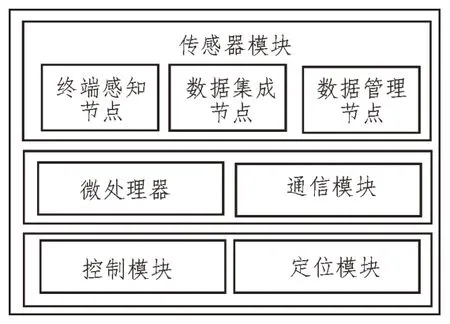
圖1 安全傳感節點架構

采用的微處理器型號為FC-3180，通信模塊關聯各傳感器節點及物聯網，采用基于WebSocket 的MQTT 協議作為通信協議，采用單片機開發控制模塊，以ATMEGA2560 為控制核心。定位模塊主要通過激光傳感器獲得定位信息，基于各模塊的功能完成機器人運動控制。

1.2 運動軌跡定位

結合基于測距到達的時間差高精度定位技術[10]與最小二乘估計策略[11]，根據待定位節點與基站的間距，通過幾何關系獲取輪式機器人具體位置。

為降低運動過程中傳感器產生的測量誤差，采用最小二乘估計算法處理節點信號，給后續定位提供精準的節點數據。具體流程如下所述：

1）根據傳感節點的信號測量值X，建立下列線性回歸模型，以獲取信號測量值X的預估值Y：

其中，α表示自變量系數，β表示偏置項。

由此推導出測量誤差向量表達式：

3）將解值X′代入回歸式（1），得到測量值的預估結果Y，即最小測量誤差的傳感信號。

假設k個基站的坐標集合是[(xa1,ya1),(xa2,ya2),…,(xak,yak)]，待定位節點坐標是(x0,y0)，利用信號誤差處理流程，優化各基站與待定位節點的傳感信號，測量兩目標之間的信號發送時長，利用下列方程式得出各目標對的距離集合(Δ1,Δ2,…,Δk)：

將式（3）代入下列矩陣式中，解得待定位目標具體坐標(x0,y0)，即機器人方位：

2 輪式機器人軌跡雙環自動控制策略

2.1 輪式機器人動力學模型優化

為精準控制機器人的運動軌跡，構建輪式機器人的動力學模型[12]。輪式機器人的輪子共有三個：一個前輪，兩個驅動與定向的后輪。假設兩后輪的半徑與間距分別是r、d，相對于水平方向的移動角度是θ，則基于歐拉-拉格朗日[13-14]的動力學模型界定公式如下所示：

式中，τ表示控制力矩；λ表示拉格朗日乘子；u表示未知擾動；F表示摩擦力；B(q)、A(q)、M(q)、C(q)分別表示轉換矩陣、非完整約束矩陣、正定矩陣、科里奧利向心力矩陣[15]。

根據廣義坐標系下的機器人位姿q=[x,y,θ]T，建立動力學模型的約束條件：

依據三角形函數定理[16]，通過下列矩陣解得機器人的位姿控制誤差e：

一階求導誤差e，將所得導數代入動力學模型界定公式（7），加強自動控制過程中誤差的穩定性，則動力學優化模型為：

2.2 基于雙環積分滑模控制技術的軌跡自動控制

利用雙環積分滑模控制技術，構建出由速度環與位置環組成的輪式機器人軌跡控制技術。設定外環為位置環，內環為速度環，前者用于控制姿態的角速度，將輸出作為內環輸入，通過網絡的應用層達成自動控制目標。

已知外環增益矩陣Dw與機器人位姿角控制誤差ew，采用下列表達式界定用于外環的積分滑模面sh：

其中，dt表示積分函數因子。

假設位姿角控制誤差ew的偏導數是，外環的三維正常數矩陣是ρw，則位置環的控制律ηw界定公式如下所示：

其中，n(ew)表示取控制誤差ew的整數值。

由此推導出基于外環積分滑模面的位置環控制模型，如下所示：

已知內環增益矩陣Dn與機器人角速度控制誤差en，采用下列表達式界定用于內環的積分滑模面s′h：

同理，結合速度環的控制律ηn界定公式（16），推導出基于內環積分滑模面的速度環控制模型，如式（17）所示：

3 實驗與結果分析

3.1 實驗準備

選取EBY-PD-2040型號輪式機器人作為實驗對象，在實驗平臺上搭建物聯網運行環境。利用平臺相關軟件模擬不同期望軌跡下的機器人控制結果，以驗證文中方法的有效性與可行性。設置機器人的實際起始位置為初始參考位置，線速度與角速度均為勻速，設定期望線速度與角速度分別為2 m/s、1 rad/s。

3.2 圓形運動軌跡控制效果分析

采用文中方法控制目標機器人的運動軌跡，控制軌跡與期望軌跡的擬合情況如圖2 所示。

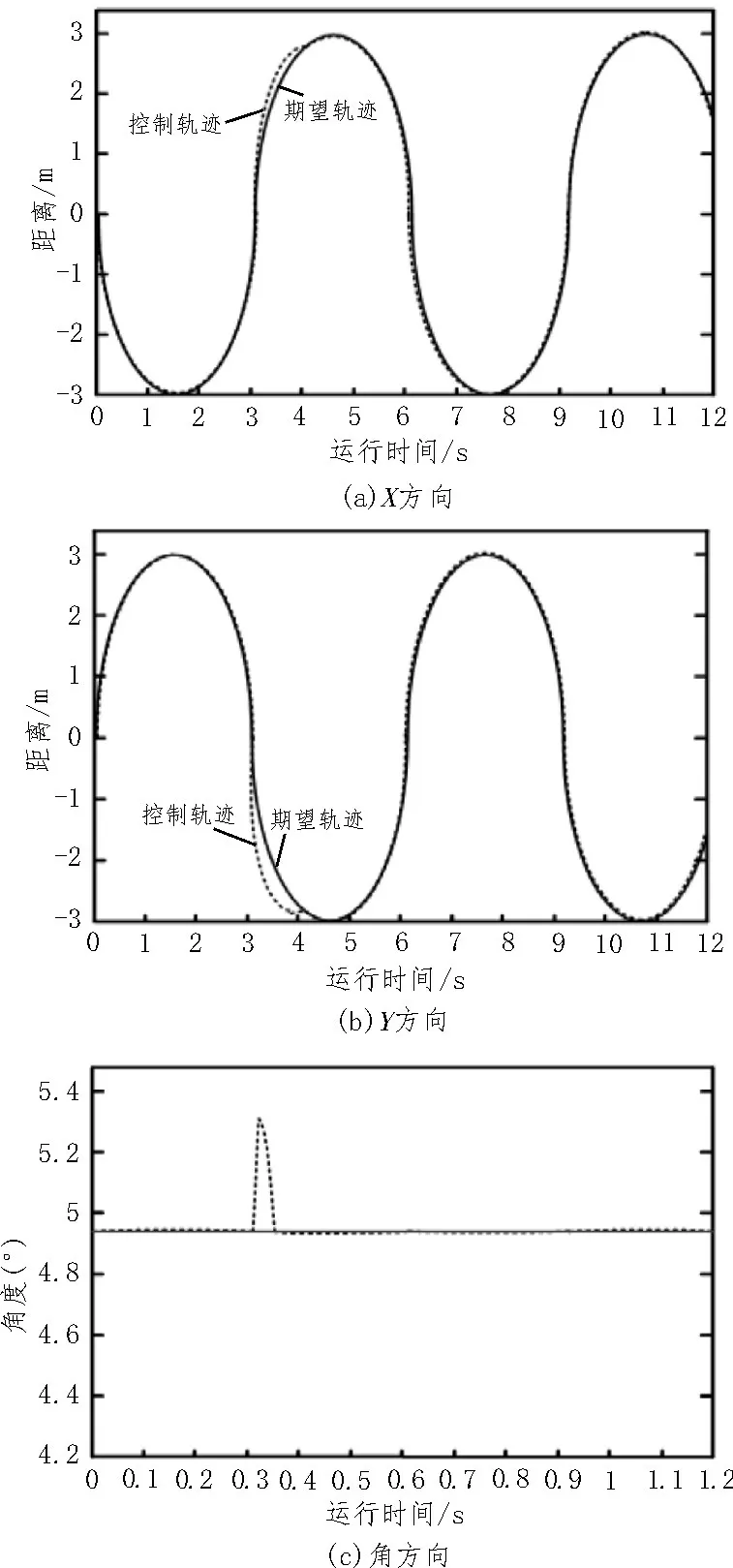
圖2 圓形運動軌跡控制結果示意圖

由圖2 可以看出，除3.1 s 左右時機器人驅動輪打滑，導致軌跡產生小幅度偏離之外，控制軌跡與期望軌跡始終保持著高度的重合狀態。該突出表現主要得益于文中傳感節點信號處理與內外環控制模型優勢，采用最小二乘估計算法降低傳感器測量誤差，通過抑制機器人非完整約束條件，利用外環控制姿態的角速度，并將輸出作為內環輸入，實時調整機器人的運動角度，使其很快返回至期望軌跡上，滿足對大多數工作環境的適應性需求。

4 結論

面向輪式機器人控制過程中控制效果不良的問題，文中提出利用雙環積分滑模控制技術，在物聯網和無線傳感網絡環境下，實現輪式機器人的運動控制。利用最小二乘估計算法補償了信號傳遞誤差，通過三角形函數定理結合期望位姿優化了動力學模型，借助雙環積分滑模控制技術輸出機器人的角速度等控制參數，從而實現輪式機器人的高精度運動軌跡控制。