淺探圓錐擺問題

2023-09-19 09:44:06華中科技大學附屬中學

中學生數理化(高中版.高考理化) 2023年9期

■華中科技大學附屬中學許文

如圖1所示,將不可伸長的輕繩一端固定,另一端系一個小球,讓小球獲得某一速度后,小球在水平面內做勻速圓周運動,在運動過程中輕繩掃過的形狀為一圓錐,則這個運動稱為圓錐擺運動。在生活中有很多類似圓錐擺的運動,以圓錐擺為背景的物理試題在近幾年的高考試卷中頻繁出現。分析圓錐擺的運動特點,探究圓錐擺的運動條件,研究圓錐擺的臨界狀態與極值問題,將有助于我們更好地將圓錐擺的運動規律應用到實際問題的求解中。

圖1

一、基本模型

設繩長為l,小球質量為m,小球做勻速圓周運動的角速度為ω,小球運動過程中輕繩與豎直方向間的夾角為θ,則小球做圓周運動的水平面與輕繩懸點間的距離(圓錐的高度)h=lcosθ。

1.運動分析。

做圓錐擺運動的小球在水平面內做勻速圓周運動。

2.受力分析。

(1)受力特點:小球受到豎直向下的重力mg、沿繩向上的拉力T,如圖2所示。在豎直方向上,合力為零,有Tcosθ=mg;在水平方向上,向心力Fn由重力mg與拉力T的合力(拉力T的水平分力)提供。

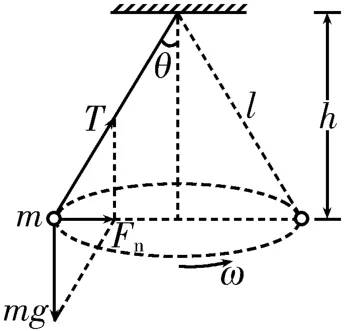
圖2

(2)大小關系:向心力大小Fn=Tsinθ=mgtanθ=mω2lsinθ,輕繩的拉力大小。

3.周期分析。

(2)特點:圓錐擺的周期T由圓錐的高度h與重力加速度g決定。

例1如圖3 所示,兒童玩具撥浪鼓上分別系有長度不等的兩根細繩,細繩一端系著小球,另一端固定在關于手柄對稱的鼓沿上。現使鼓繞豎直放置的手柄勻速轉動,兩小球在水平面內做周期相同的勻速圓周運動。兩球的位置關系可能正確的是(圖4 中細繩與豎直方向間的夾角α＜θ＜β)( )。

圖3

解析：手柄勻速轉動,穩定后兩小球均做周期為T的圓錐擺運動。設鼓的半徑為r,繩長為l,細繩與豎直方向間的夾角為θ,則繩長的豎直分量h=lcosθ;由小球的重力與細繩拉力的合力提供向心力,則mgtanθ=,變形得因此當轉動周期T相同時,若細繩與豎直方向間的夾角θ越大,則繩長的豎直分量h越大。由α＜θ＜β可知,只有選項C正確。

答案：C

點評:鼓隨手柄勻速轉動,用輕繩系于鼓沿上的兩小球穩定時做與手柄轉動周期相同的圓錐擺運動。小球在水平面內做圓周運動的軌跡半徑為r+lsinθ。上述求解過程是基于小球做圓錐擺運動由重力和拉力的合力提供向心力得到關于T、θ及h的函數關系而得出的。若充分利用圓錐擺的周期由圓錐的高度與重力加速度決定這一特點,結合題給條件α＜θ＜β,畫出如圖5 所示的小球做圓錐擺運動的圓錐高度H,借助幾何圖形進行分析判斷,則很容易選出正確答案為C。

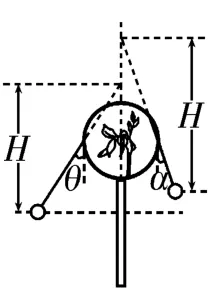
圖5

二、拓展模型

生產生活中有很多運動的受力特點與運動性質與圓錐擺類似,我們把這類運動均稱為類圓錐擺運動。生產生活中常見的類圓錐擺運動(彈力N相當于圓錐擺基本模型中的繩子拉力T)有:

1.小球沿光滑漏斗內壁在水平面內做勻速圓周運動,受力情況如圖6甲所示。

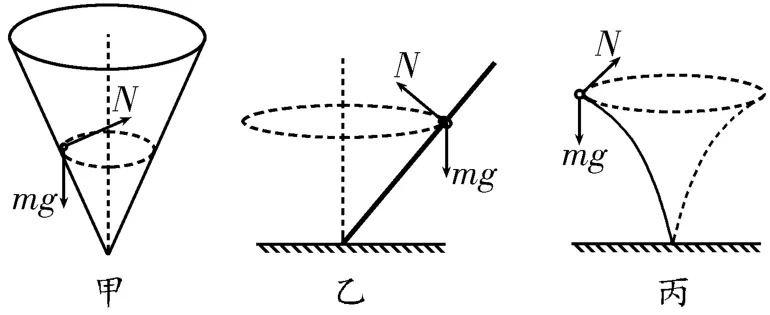
圖6

2.套在光滑細桿上的小環隨桿在水平面內做勻速圓周運動,受力情況如圖6乙所示。

3.固定在彈性細桿一端的小球隨桿在水平面內做勻速圓周運動,受力情況如圖6 丙所示。

4.小球穿在光滑豎直圓環上隨圓環在水平面內做勻速圓周運動,受力情況如圖7 甲所示。

圖7

5.火車在內低外高的圓弧彎道路面上轉彎時內外軌均無側向擠壓,或汽車不受徑向摩擦力,在水平面內做勻速圓周運動,受力情況如圖7乙所示。

6.滑冰女運動員在男運動員的拉力作用下在水平面內做勻速圓周運動(女運動員恰好離開水平冰面),受力情況如圖7丙所示。

例2某同學在乘坐列車的過程中研究列車的運動情況。他在車廂頂部用細線懸掛一個小熊玩具,當列車以恒定速率通過一段彎道時,發現懸掛小熊玩具的細線與車廂側壁平行,如圖8所示。下列判斷正確的是( )。

圖8

A.細線對玩具的拉力大小等于玩具的重力大小

B.外側軌道與輪緣間沒有側向擠壓作用

C.內側軌道與輪緣間沒有側向擠壓作用

D.如果知道轉彎處內、外軌道所在斜面的傾角,就可以求出列車轉彎時的速率

解析：設列車轉彎時內、外軌道所在斜面的傾角為θ,玩具的質量為m。懸掛玩具的細線與車廂側壁平行,即細線垂直于內、外軌道所在的斜面,因此細線與豎直方向間的夾角為θ,玩具在豎直方向上受到的合力為零,則Tcosθ=mg,解得,選項A 錯誤。玩具隨列車一起在水平面內做勻速圓周運動,根據細線的拉力T與玩具的重力mg的合力提供向心力得mgtanθ=man,解得列車轉彎時的向心加速度大小an=gtanθ。根據牛頓第二定律可知,車廂的重力與軌道的支持力的合力產生的加速度大小為gtanθ,故列車在轉彎時的運動相當于圓錐擺運動,這時列車的內、外軌道與輪緣間均沒有側向擠壓作用,選項B、C 正確。由得,在傾角θ與轉彎處的圓弧半徑r均已知的情況下,可以求出列車轉彎時的速率v,選項D 錯誤。

答案：BC

點評:小熊玩具隨列車一起做圓周運動,它們的向心加速度大小相同;根據小熊玩具的受力情況推知向心加速度的大小,根據列車的向心加速度大小推知列車此時做類圓錐擺運動,從而可判斷列車的受力情況。

三、臨界問題

臨界狀態是變化的物理量取某種特征值所表現出來的一種特殊狀態。當圓錐擺擺線長度一定時,其運動的角速度存在一個最小值;當圓錐擺運動的角速度一定時,圓錐擺的擺長也存在一個最小值。圓錐擺問題常見的臨界狀態如表1所示。

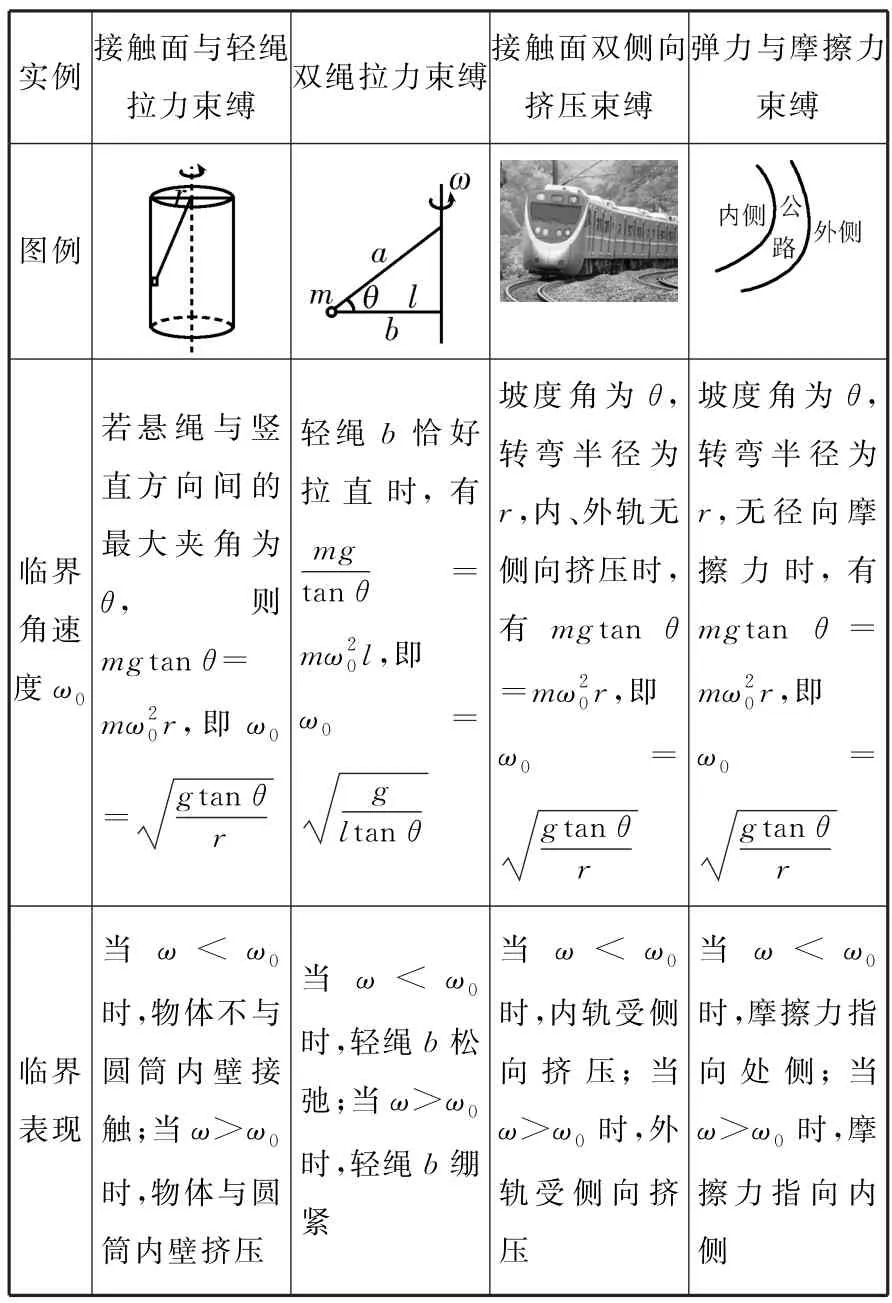
表1

例3如圖9所示,兩根輕繩AC、BC同系一質量m=0.1 kg的小球,兩輕繩的另一端分別固定在豎直細桿上的A、B兩點,輕繩AC的長度L=2 m,當兩輕繩均拉直時,兩輕繩與細桿間的夾角分別為α=30°和β=45°,取重力加速度g=10 m/s2。當小球隨桿一起以角速度ω=4 rad/s轉動時,兩輕繩對小球的拉力大小各為多少?

圖9

解析：小球在重力與輕繩拉力的作用下隨桿一起轉動時,小球做圓錐擺運動。當兩輕繩分別恰好拉直時對應著小球做圓錐擺運動的兩個臨界狀態。

若轉動角速度為ω1時輕繩BC恰好拉直,則此時輕繩AC對小球的拉力FA與小球重力mg的合力提供小球做圓周運動所需的向心力,有,解得ω1=2.4 rad/s。

若轉動角速度為ω2時輕繩AC恰好拉直,則此時輕繩BC對小球的拉力FB與小球重力mg的合力提供小球做圓周運動所需的向心力,有,解得ω2=3.15 rad/s。

因此當2.4 rad/s≤ω≤3.15 rad/s時,AC、BC兩輕繩均處于繃緊狀態。因為ω=4 rad/s＞ω2,所以此時輕繩AC松弛,即FA=0。根據受力分析得FBcosβ=mg,FBsinβ=mω2r,根據幾何關系得r=LBCsinβ=Lsinα,解得FB=2.26 N。

點評:小球做圓錐擺運動的角速度ω≤ω1時輕繩BC松弛,ω≥ω2時輕繩AC松弛。先通過對小球臨界狀態的分析得出兩個臨界角速度,再將題給角速度與臨界角速度相比較,即可確定小球的運動狀態,從而可求出兩輕繩對小球的拉力。

跟蹤訓練

1.智能呼啦圈輕便美觀,深受大眾喜愛。智能呼啦圈的腰帶外側帶有軌道,將帶有滑輪的短桿穿入軌道,短桿的另一端懸掛一根帶有配重的輕繩,其簡化模型如圖10 所示。可視為質點的配重質量為0.5 kg,繩長為0.5 m,懸掛點P到腰帶中心點O的距離為0.2 m,水平固定好腰帶,通過人體微小扭動,使配重隨短桿在水平面內做勻速圓周運動,輕繩與豎直方向間的夾角為θ,運動過程中腰帶可視為保持不動,取重力加速度g=10 m/s2,下列說法中正確的是( )。