三力平衡問題的求解策略
———以“輕繩、輕桿模型”為例

■山東省臨沂第十八中學 張 宇

■山東省臨沂第十九中學 夏宗平

共點力平衡是指物體受到幾個力的作用處于平衡狀態,即處于靜止或勻速直線運動狀態。三力平衡是共點力平衡問題中的一個考查熱點,也是難點,求解三力平衡問題對同學們的理解能力、空間想象能力、邏輯推導能力和應用數學知識解決物理問題能力的要求都較高。下面以“輕繩、輕桿模型”中的三力平衡問題為例,論述如何透過表面現象,抓住各種題型的本質特征,找到相應的解題方法,供同學們參考。

一、三力靜態平衡問題

例1如圖1所示,水平輕桿BC的B端用鉸鏈固定在豎直墻壁上,輕繩AD拴接在輕桿C端,D端所掛物體質量為m,輕繩AC段與水平方向間的夾角α=30°,取重力加速度g=10 m/s2,求輕繩AC的拉力T的大小,以及輕桿BC對結點C的支持力N。

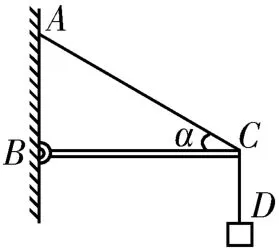
圖1

指點迷津：本題是平衡問題中典型的死結、活桿模型,以結點C為研究對象,分析輕繩時要特別注意輕繩AC段是拴接在C點的,其拉力不等于物體的重力,分析輕桿時要特別注意與鉸鏈相連的桿上的作用力一定沿桿的方向。

解法1：力的合成法。對結點C進行受力分析,以T和N為鄰邊作平行四邊形,其對角線與mg大小相等,方向相反,如圖2所示。根據幾何關系得,方向水平向右。

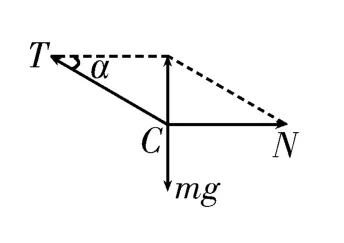
圖2

解法2：正交分解法。對結點C進行受力分析并正交分解,如圖3 所示。根據幾何關系得Tx=Tcosα,Ty=Tsinα。根據平衡條件得Tx=N,Ty=mg。聯立以上各式解得,方向水平向右。

圖3

點評:已知三個力的方向且其中兩個力存在垂直關系是三力靜態平衡問題中最常見的題型。解題時既可以利用力的合成法,先構建平行四邊形找到直角三角形,再利用三角函數關系進行求解;也可以利用正交分解法,先以相互垂直的兩個力的方向為x、y軸建立平面直角坐標系,將不在坐標軸上的那個力分解到坐標軸上,再利用平衡關系進行求解。

變式1：如圖4 所示,輕桿BC的B端用鉸鏈固定在水平地面上,輕繩AD拴接在輕桿C端,D端所掛物體質量為m,輕繩AC段與水平方向間的夾角α=30°,輕桿BC與水平方向間的夾角β=45°,取重力加速度g=10 m/s2,求輕繩AC的拉力T的大小,以及輕桿BC對結點C的支持力。

圖4

答 案：,方向與水平方向成45°角斜向右上方。 提示:已知的三個力不存在某兩個力的方向始終垂直的關系,無法構建直角三角形,但可以用正交分解法進行求解。對結點C進行受力分析并正交分解,如圖5所示。根據幾何關系得Tx=Tcosα,Ty=Tsinα,Nx=Ncosβ,Ny=Nsinβ。根據平衡條件得Tx=Nx,Ny=Ty+mg。聯立以上各式解得,方向與水平方向成45°角斜向右上方。

圖5

變式2：如圖6 所示,輕繩AD跨過固定在水平橫梁BC右端的定滑輪懸掛一個質量為m的物體,輕繩AC段與水平方向間的夾角α=30°,取重力加速度g=10 m/s2。求輕繩AC段的張力T的大小,以及橫梁BC對C點的支持力。

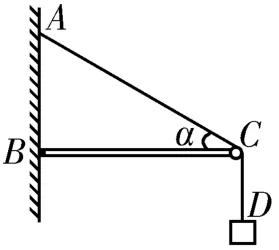
圖6

答案：T=mg;N=mg,方向與豎直方向成60°角斜向右上方。 提示:已知兩個力的大小和方向且兩個力存在相等關系,而第三個力的方向未知,用力的合成法構建菱形可知第三個力一定在前兩個力的角平分線上,根據三角形的邊長關系即可求出第三個力的大小。對C點進行受力分析,則T=mg,以T和mg為鄰邊作平行四邊形,其對角線與N大小相等,方向相反,如圖7 所示。根據幾何關系得N=mg,方向與豎直方向成60°角斜向右上方。

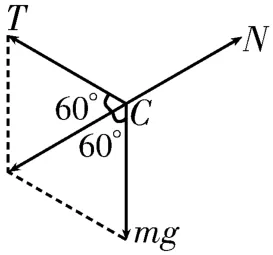
圖7

二、三力動態平衡問題

例2如圖8所示,用輕繩OA、OB懸掛一物體處于平衡狀態,輕繩OA與豎直方向成一夾角,輕繩OB水平。當輕繩OA的懸點A緩慢向右移動時,輕繩OB始終保持水平。設此過程中輕繩OA、OB的拉力分別為FOA、FOB,下列說法中正確的是( )。

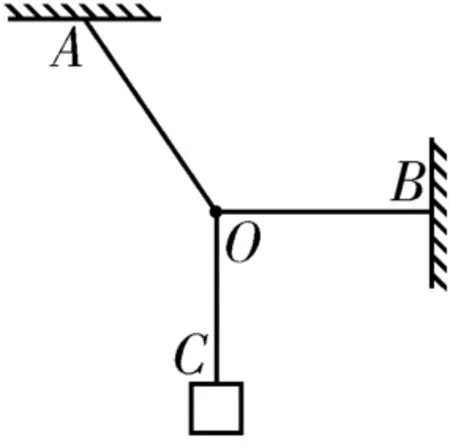
圖8

A.FOA一直減小

B.FOA先減小后增大

C.FOB一直減小

D.FOB先增大后減小

指點迷津：在對O點進行受力分析時要特別注意當輕繩OA的懸點A向右移動時,FOC的大小和方向均不變,FOB的方向不變,FOA的方向發生變化,需要抓住“變化“與“平衡”間的關系。

解法1：解析法。對初狀態O點進行受力分析,設FOA與豎直方向間的夾角為θ,以FOA和FOB為鄰邊作平行四邊形,其對角線與mg大小相等,方向相反,如圖9 所示。根據幾何關系得。當輕繩OA的懸點A緩慢向右移動時,θ減小,根據三角函數的單調性得FOA一直減小,FOB也一直減小。

圖9

解法2：圖解法。以初狀態O點為研究對象,其受到的mg、FOA、FOB可構成矢量三角形,如圖10 所示。當輕繩OA的懸點A緩慢向右移動時,FOA與豎直方向間的夾角減小,需要將FOA的方向繞重力的末端沿順時針方向旋轉形成新的矢量三角形,觀察變化的矢量三角形可以看出FOA、FOB均逐漸減小。

圖10

答案：AC

點評:本題是三力動態平衡問題中一個力的大小和方向均不變,一個力的方向不變,一個力的方向發生變化類題型。因為三個力中FOB和mg始終存在垂直關系,所以既可以利用力的合成法,先構建平行四邊形找到直角三角形,再利用三角函數的單調性進行求解;也可以利用圖解法,將三力首尾相連構成矢量三角形,當FOA方向發生變化時比較矢量三角形線段的長度變化即可判斷力的變化情況。

變式3：如圖11所示,用輕繩OA、OB懸掛一物體處于平衡狀態,開始時輕繩OB水平。現保持O點位置不變,改變輕繩OB的長度使輕繩右端由B點緩慢上移至B'點,此時輕繩OB'與OA之間的夾角θ＜90°。設此過程中輕繩OA、OB的拉力分別為FOA、FOB,下列說法中正確的是( )。

圖11

A.FOA一直減小

B.FOA一直增大

C.FOB一直減小

D.FOB先增大后減小

答案：A 提示:雖然FOB的方向發生變化,使得三個力不存在某兩個力的方向始終垂直的關系,無法構建直角三角形,但可以用圖解法進行求解。以初狀態O點為研究對象,其受到的mg、FOA、FOB可構成矢量三角形,如圖12所示。當B點緩慢向上移動時,FOB與豎直方向間的夾角減小,需要將FOB的方向繞重力的末端沿逆時針方向旋轉形成新的矢量三角形,直至FOA與FOB之間的夾角小于90°,觀察變化的矢量三角形可以看出FOA逐漸減小,FOB先減小后增大。

圖12

例3如圖13所示,輕繩與輕桿承受彈力的最大值一定,輕桿的C端用鉸鏈固定,光滑輕小滑輪在C點正上方,B端吊一重物,現將輕繩的一端拴在輕桿的B端,用拉力F將B端緩慢上拉,在輕桿BC達到豎直前(輕繩與輕桿均未斷),關于輕繩的拉力FAB和輕桿受到的彈力FBC的變化,下列說法中正確的是( )。

圖13

A.FAB增大 B.FAB減小

C.FBC增大 D.FBC減小

指點迷津：在對B點進行受力分析時要特別注意將B端緩慢上拉時,FBD(等于重物的重力)的大小和方向均不變,FAB和FBC的方向均發生變化,需要找到圖中暗含的空間幾何三角形和力的矢量三角形的相似關系。

解析：對結點B進行受力分析,以FAB和FBC為鄰邊作平行四邊形,其對角線與mg大小相等,方向相反,如圖14 所示。根據空間幾何三角形ABC與力的矢量三角形相似得。將B端緩慢上拉的過程中,AC、BC邊的長度不變,AB邊的長度減小,所以FBC不變,FAB減小。

圖14

答案：B

點評:本題是三力動態平衡問題中一個力的大小和方向均不變,另外兩個力的方向均發生變化類題型。需要在正確受力分析的基礎上先作出平行四邊形,再找到相似的幾何三角形與力的矢量三角形,由對應邊成比例寫出等式進行計算、推理即可得出答案。

變式4：如圖15 所示,裝置中兩根細繩拴住一小球,保持兩細繩間的夾角θ=120°不變,若把整個裝置沿順時針方向緩慢轉過90°,則在轉動過程中,關于兩細繩的拉力FCA和FCB的變化,下列說法正確的是( )。

圖15

A.FCA先減小后增大

B.FCA先增大后減小

C.FCB先減小后增大

D.FCB一直減小,且最終減小為零

答案：BD 提示:在裝置緩慢轉動的過程中,小球重力mg的大小和方向均不變,FCA和FCB的方向均發生變化但它們的夾角始終保持不變,可以利用“同圓中同弦所對的圓周角相等”建構一個輔助圓進行求解。以初狀態小球為研究對象,其受到的mg、FCA、FCB可構成矢量三角形,畫矢量三角形的外接圓,保持恒力mg這條弦不變,在CA由水平方向緩慢轉到豎直方向的過程中,保持FCA與FCB的夾角不變,畫出三個力動態平衡的矢量三角形,如圖16 所示。由圖可以看出,FCA先增大后減小,FCB一直減小,且最終減小為零。

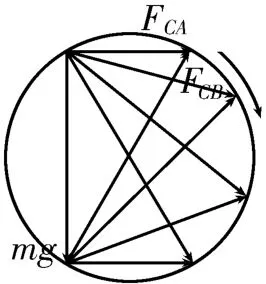
圖16