力學動態平衡問題歸類剖析

■河北樂亭第一中學 王金濤

動態平衡指的是因為某種物理量的改變,物體所處的狀態緩慢變化,而在這個緩慢變化的過程中,物體一直處于平衡狀態。當物體處于動態平衡狀態時,所受的外力會發生變化,但是所受合外力會一直等于零。因此解決這類問題最重要的是在變化中尋找到不變,利用不變的量確定變量的變化規律。下面歸納總結了求解力學動態平衡問題的幾種常見方法,供同學們參考。

一、動態圖解法

原理：對物體在狀態變化過程中的多種平衡狀態進行受力分析,以某一參量的變化為基礎,在同一圖中作出物體在多種平衡狀態下的受力示意圖(力的平行四邊形),根據動態的力的平行四邊形各邊長度和角度的變化,確定力的大小及方向的變化情況。

適用條件：物體受到三個共點力作用處于動態平衡狀態,其中一個力是大小和方向均不變的恒力;另外一個力的方向不變,大小變化;第三個力的大小和方向都變化。

例1如圖1 所示,用細繩系住小球放在傾角為θ的光滑斜面上,當細繩由水平方向逐漸向上偏移時,小球對細繩的拉力T和對斜面的壓力N的變化情況是( )。

A.T逐漸增大,N逐漸減小

B.T逐漸減小,N逐漸增大

C.T先增大后減小,N逐漸減小

D.T先減小后增大,N逐漸減小

解析：對小球進行受力分析,小球受到重力mg(大小和方向均不變的恒力)、斜面的支持力N'(方向不變,大小變化)和細繩的拉力T'三個力的作用。在同一個圖中作出細繩由水平方向逐漸向上偏移的過程中多個平衡狀態下小球的受力示意圖,如圖2 所示。根據圖像可知,隨著細繩由水平方向向上偏移,細繩的拉力T'先減小后增大,斜面的支持力N'逐漸減小。根據牛頓第三定律可知,小球對細繩的拉力T先減小后增大,小球對斜面的壓力N逐漸減小。

圖2

答案：D

二、正交分解法

原理：當物體處于動態平衡狀態時,先對物體進行正確的受力分析,再建立平面直角坐標系,將不在坐標軸上的力正交分解,以具體情況為依據,引入參數,構建平衡方程,得出因變參數與自變參數之間的一般函數關系,然后以自變量的變化為依據確定因變量的變化,進而判斷力的大小變化規律。

例2如圖3 所示,物體靜止在斜面上,斜面對物體的支持力為N,物體受到的摩擦力為f,則當斜面傾角θ變小時,下列說法中正確的是( )。

圖3

A.N變小,f變小

B.N變小,f變大

C.N變大,f變小

D.N變大,f變大

解析：對物體進行受力分析,物體受到重力G、斜面的支持力N和摩擦力f三個力作用。以沿斜面向上為x軸正方向,以垂直于斜面向上為y軸正方向建立平面直角坐標系,將重力G正交分解,如圖4 所示。根據平衡條件可得,在x軸方向上有f=Gsinθ,在y軸方向上有N=Gcosθ。當斜面傾角θ變小時,sinθ變小,cosθ變大,f變小,N變大。

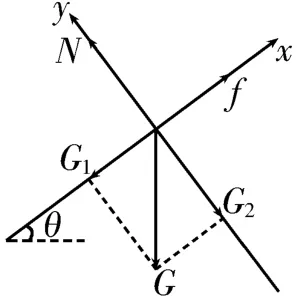
圖4

答案：C

三、相似三角形法

原理：當物體受到三個共點力作用而處于動態平衡狀態時,先對物體進行正確的受力分析,并畫出受力示意圖,再在圖中尋找與力的矢量三角形相似的幾何三角形,利用相似三角形的性質,構建出比例關系,把力的大小變化問題轉換成幾何三角形邊長的大小變化問題,展開討論。

例3如圖5所示,光滑半球固定在水平地面上,球心O的正上方固定一個小定滑輪,細繩一端拴一小球,小球置于半球面上的A點,細繩另一端繞過定滑輪用手拉住。現緩慢拉繩使小球從A點滑到半球面的頂點,在此過程中,小球對半球的壓力N及細繩的拉力F的變化情況是( )。

A.N變大,F變大

B.N變小,F變大

C.N不變,F變小

D.N變大,F變小

解析：對小球進行受力分析,小球受到重力G、半球面的支持力N和細繩的拉力F三個力作用。作出小球受力的矢量三角形,并連接球心O和A點,構建幾何三角形OAB,如圖6所示。根據由G、N、F構成的矢量三角形與幾何三角形OAB相似得, 在小球從A點滑到半球面頂點的過程中,OA不變,OB不變,AB減小,G不變,則N不變,F變小。

圖6

答案：C

四、矢量圓法

原理：當物體受到三個共點力作用而處于動態平衡狀態時,如果其中一個力是大小和方向均不變的恒力,另外兩個力的夾角保持不變,那么可以先作出力的矢量三角形,再作出該矢量三角形的外接圓,觀察隨著研究對象的緩慢移動,矢量三角形的頂點在圓周上的移動情況,從而分析判斷力的變化情況。

適用條件：物體受到三個力作用處于動態平衡狀態,其中一個力是大小和方向均不變的恒力,另外兩個力的大小和方向均變化,但二者的夾角保持不變。

例4如圖7所示,置于水平地面上的豎直圓形金屬環內用三根細繩OA、OB、OC懸掛一質量為m的物體,物體可視為質點。初始狀態下,細繩OB沿水平方向,∠AOB=120°。設細繩OA、OB的張力大小為F1、F2,現將金屬圓環在豎直面內緩慢沿逆時針方向轉過90°,在此過程中( )。

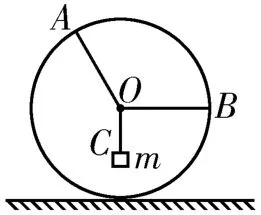
圖7

A.F1一直增大

B.F2一直增大

C.F1先增大后減小

D.F2先增大后減小

解析：選結點O為研究對象,對它進行受力分析,結點O受到細繩OA、OB、OC的拉力作用,其中細繩OA、OB的拉力的夾角保持不變,細繩OC的拉力等于物體的重力mg。作出結點O受力的矢量三角形,并作矢量三角形的外接圓,如圖8 所示。觀察圖像可知,將金屬圓環在豎直面內緩慢沿逆時針方向轉過90°的過程中,θ=180°-∠AOB=60°保持不變,細繩OC的拉力(mg)的大小和方向均不變,F1一直減小,F2先增大后減小。

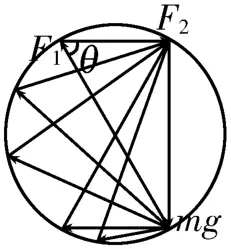
圖8

答案：D

五、整體法和隔離法

原理：整體法是將物理問題中的兩個或兩個以上物體視為一個整體進行分析和研究的方法,隔離法是將單個物體與整體分開進行分析和研究的方法。當分析由兩個或兩個以上物體構成的系統的動態平衡問題時,經常需要將整體法和隔離法結合運用。

例5如圖9所示,橫截面為四分之一圓、質量為M的柱體B放在粗糙水平地面上,一豎直固定的擋板與柱體B最左側相切,質量為m的小球a恰能靜止在擋板和柱體之間。現拿走小球a,將質量也為m、但密度比小球a小的小球b貼著擋板輕輕放到擋板與柱體B之間。小球與擋板、小球與柱體B之間的摩擦忽略不計。下列說法中正確的是( )。

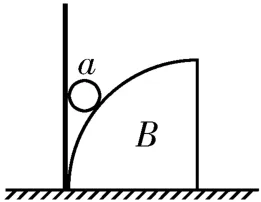
圖9

A.小球b對擋板的壓力大于小球a對擋板的壓力

B.小球b對柱體B的壓力大于小球a對柱體B的壓力

C.地面對柱體B的支持力不變

D.柱體B受到地面的摩擦力不變

解析：以小球a為研究對象,其受力分析示意圖如圖10甲所示。根據平衡條件可知,擋板與柱體B對小球a作用力F1、F2的合力與小球a的重力大小相等、方向相反。小球b與小球a相比,質量不變、體積增大,則柱體B的橫截面圓心和小球b球心的連線與豎直方向間的夾角減小(圖10 甲中的F2繞力的作用點沿順時針方向旋轉),根據力的平行四邊形定則和牛頓第三定律可知,小球b對擋板的壓力小于小球a對擋板的壓力,小球b對柱體B的壓力小于小球a對柱體B的壓力,選項A、B錯誤。

圖10

以由小球a和柱體B組成的整體為研究對象,其受力分析示意圖如圖10 乙所示。根據平衡條件可知,在水平方向上有f=F1,在豎直方向上有N=(M+m)g。將小球a換作小球b之后,因為F1減小,所以柱體B所受地面的摩擦力f減小,選項D 錯誤;因為兩小球的質量相等,所以地面對柱體B的支持力N不變,選項C正確。

答案：C

跟蹤訓練

1.如圖11所示,一小球放置在木板與豎直墻面之間。設墻面對小球的壓力大小為N1,小球對木板的壓力大小為N2。以木板與墻面連接點所形成的水平直線為軸,將木板從圖示位置開始緩慢地轉到水平位置。不計一切摩擦,在此過程中( )。

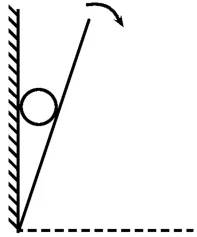
圖11

A.N1一直減小,N2一直增大

B.N1一直減小,N2一直減小

C.N1先增大后減小,N2一直減小

D.N1先增大后減小,N2先減小后增大

2.如圖12 所示,裝有足球的輕網兜系在釘子上,墻壁光滑。將網繩在釘子上多繞幾圈后,下列判斷正確的是( )。

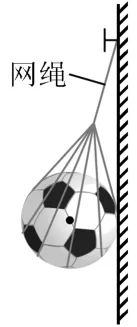
圖12

A.網繩的拉力變小

B.網繩的拉力不變

C.墻壁對足球的支持力變大

D.墻壁對足球的支持力不變

3.如圖13所示,豎直平面內有輕繩1、2、3拴接在O點。輕繩1 水平,輕繩2與水平方向成60°角,輕繩3 的下端連接一質量為m的導體棒a,在結點O正下方2d距離處固定一導體棒b,兩導體棒均垂直于豎直平面放置。現將導體棒a中通入向里的電流I0,將導體棒b中通入向外且緩慢增大的電流I。當電流I增大到某個值時,給導體棒a以向右的輕微擾動,可觀察到它緩慢上升到輕繩1所在的水平線上。已知輕繩3的長度為d,兩導體棒的長度均為l,重力加速度為g,導體棒b以外距離為x處的磁感應強度。下列說法中正確的是( )。

圖13

D.導體棒b中電流的最大值

4.如圖14 所示,AB、BC兩塊木板構成夾角為60°的“V”形角架,其間放置一質量為m的圓球,整體豎直放置在水平桌面上,繞B點為轉軸緩慢沿順時針方向轉動角架,不計一切摩擦,重力加速度為g,下列說法中正確的是( )。

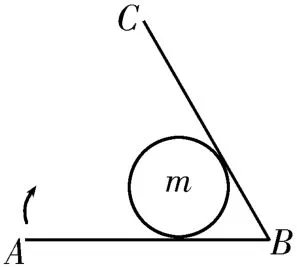
圖14

A.木板AB受到的彈力逐漸減小

B.木板AB受到的彈力先減小后增大

C.木板BC受到的彈力逐漸增大

5.如圖15 所示,光滑豎直墻壁與光滑水平地面交于B點,質量為M的光滑半圓柱體,緊靠豎直墻壁置于水平地面上,O為半圓柱體橫截面的圓心。質量為m且可視為質點的小球,用長度為L的細線懸掛于豎直墻壁上的A點,小球靜置于半圓柱體上。當換用質量不變,而半徑不同的光滑半圓柱體時,細線與豎直墻壁間的夾角θ就會跟著發生改變。已知A、B兩點間的距離也為L,重力加速度為g,不計各接觸面間的摩擦。下列說法中正確的是( )。

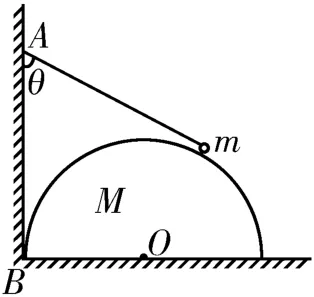
圖15

A.當θ=60°時,細線對小球的拉力大小為

B.當θ=60°時,半圓柱體對小球的支持力大小為

C.在θ逐漸減小的過程中,半圓柱體受到水平地面的彈力始終保持不變

D.在θ逐漸減小的過程中,半圓柱體受到豎直墻壁的彈力始終保持不變

參考答案：1.B 2.C 3.B 4.D 5.A