高速鋼軌RCF裂紋渦流檢測仿真系統及應用

于亞婷,袁 飛,熊龍輝,田貴云

(1. 電子科技大學機械與電氣工程學院,四川 成都 6117312. 中國鐵道科學研究院集團有限公司基礎設施檢測研究所,北京 100081;3. 電子科技大學自動化工程學院,四川 成都 611731)

1 引言

中國高鐵規劃建設起步較晚,但從2003年第一條高鐵—“秦沈客運專線”建成到2020年底,我國鐵路運營總里程預計將達到14.6萬千米,最高時速可達到350千米/時[1-2]。高速鐵路的快速發展滿足了人民群眾出行、運輸需求,順應我國經濟快速發展要求。然而,高鐵事故的發生直接危害到生命財產安全,所以對高速軌道服役期間的損傷進行快速定期檢測和維護工作是重中之重[3]。目前常見的高鐵鋼軌傷損有滾動接觸疲勞損傷、內部核傷、腐蝕裂紋等。其中,鋼軌滾動接觸疲勞(Rolling Contact Fatigue:RCF)傷損最為常見,其包括軌頭表面的斜裂紋、軌頭內部隱傷和軌頭的剝離掉塊三種類型[4]。

目前,我國高速鋼軌常用的材料為U71Mn、U75V和U76CrRE三種鋼種,不同鋼種的化學成分占比不同,其中,U76CrRE的主要成分包括C、Si、Mn、Cr等[5],該合金鋼具有很強的導電性和導磁性。針對高導電性和高導磁性材料,電磁無損檢測被證明是最有效和最適合的方法[6]。但是針對高速鋼軌疲勞接觸裂紋的電渦流無損檢測技術中涉及動態/靜態問題、電場和磁場的耦合問題,還需開展進一步的研究。

目前針對在靜態情形下的電磁無損檢測電磁場的計算,Dodd和Deeds、Theodoulidis、李勇等[7-12]基于電磁場理論建立不同的解析模型,結合分離變量法和截斷區域法等數學方法得到解析表達式。然而建立的解析模型大都是針對無裂紋的金屬構件展開的。為了對高鐵軌道疲勞接觸裂紋的檢測提供理論支持,作者和Theodoulidis等人推導了含有圓柱裂紋、橢圓柱裂紋和矩形裂紋的金屬構件電磁無損檢測電磁場解析計算表達式[13-14],然而電磁場的解析計算涉及電磁場、數學、數值計算等多學科基礎理論,因此計算過程繁復。

同時,針對高速運行情況下鋼軌裂紋的無損檢測,作者等提出基于動生渦流的直流電磁無損檢測方法是實現金屬構件中裂紋快速檢測的可行方法[15]。對高速運行下含裂紋鋼軌的直流電磁無損檢測的電磁場進行數值模擬是認識和理解在運動情形下鋼軌中電磁場分布的重要手段。然而,基于動生渦流的直流電磁無損檢測電磁場仿真建模過程因涉及瞬態分析、涉及多個物理場,所以建模過程較為復雜,計算時間較長。

為此,為深入理解電渦流無損檢測中電場和磁場的耦合關系,理解靜態和高速運行狀態下高速鋼軌中電磁場的分布,有必要構建高速鋼軌疲勞接觸裂紋電渦流檢測評估仿真系統,降低電渦流無損檢測中靜態電磁場解析計算復雜程度以及動態電磁場的建模難度。提升獲取靜態電磁場和動態電磁場分布的效率,為提出高鐵鋼軌中疲勞接觸裂紋的定量無損檢測方法提供支撐。為此,本文基于.NET技術設計了靜態和動態情形下高速鋼軌滾動疲勞裂紋的電渦流無損檢測評估仿真系統,旨在避免復雜推導過程和復雜建模過程的情形下,充分理解含有裂紋的金屬構件在動/靜態電磁無損檢測中電場和磁場的耦合規律,最后將該系統應用于確定動/靜態情形下電磁場的分布和RCF參數之間的定量關系。

2 基礎理論

2.1 含裂紋金屬構件電渦流無損檢測靜態電磁場計算方法

渦流檢測技術是利用電磁感應原理,通過測定被檢工件內感生渦流的變化來無損評定導電材料及其工件的某些性能,或發現裂紋的無損檢測。在渦流檢測技術中,當線圈中通入交流電后線圈周圍將會產生磁場,變化的磁場感應被測的金屬試件表面產生渦流,變化的渦流產生二次感應磁場與原磁場疊加使線圈的復阻抗發生變化,當金屬試件有裂紋時,通過檢測線圈的復阻抗的變化或者磁傳感器電壓的變化檢測該試件的裂紋參數,其檢測原理過程如圖1所示。

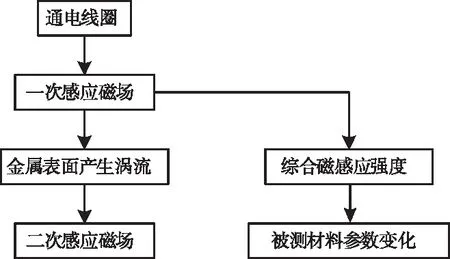
圖1 電磁渦流檢測基本原理

為模擬鋼軌中的真實裂紋,作者建立了含有矩形裂紋的金屬構件的電磁無損檢測電磁場解析計算模型[13]。主要思路如圖2所示。首先計算含有圓柱裂紋的金屬構件的電磁無損檢測電磁場解析計算表達式。然后通過最小誤差法將其擴展到含橢圓柱裂紋的電磁無損檢測電磁場解析計算表達式。最后通過面積相等、裂紋長、寬與橢圓長軸和短軸成比例的等效方法獲得含有矩形裂紋的金屬構件電磁無損檢測電磁場半解析計算模型。其中含有柱狀裂紋的金屬構件的電磁渦流電磁場計算是獲取含矩形裂紋金屬構件電磁無損檢測電磁場計算關鍵。

圖2 含矩形裂紋的金屬構件電磁無損檢測電磁場計算思路

2.2 基于直流電磁激勵動生渦流的鋼軌RFC裂紋檢測原理

動生渦流是指當電磁檢測裝置(探頭)與金屬構件之間存在相對運動時,金屬構件表面所產生的渦流。根據法拉第電磁感應定律,金屬構件表面的動生渦流可表示為

Jm=σv×B

(1)

動生渦流檢測技術是指在激勵線圈中通入直流電產生恒定磁場,通過探頭與金屬構件(例如鋼軌)之間的相對運動在金屬構件表面產生的動生渦流而對金屬表面裂紋進行檢測,如圖3所示。在動生渦流檢測系統中,根據麥克斯韋方程組以及式(1),探頭與運動金屬構件的控制方程可寫為:

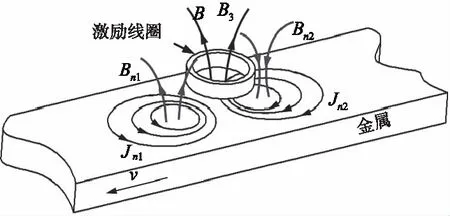
圖3 動生渦流裂紋檢測磁場圖

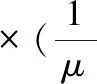
(2)

式中,μ為金屬構件的磁導率,A為磁矢量勢(B=?×A),J0為激勵線圈所產生的恒定磁場。

根據楞次定律,圖3中動生渦流Jm可表示為Jn1和Jn2,Jn1和Jn2方向相反。Jn1和Jn2產生磁場分別為Bn1和Bn2,其方向由安培定律確定。如金屬構件為鋼軌等鐵磁性材料,鐵磁性材料將會被檢測系統內部的磁場磁化而產生磁化場,記為B3。因此,根據式(2),當金屬構件表面不存在裂紋時,動生渦流檢測系統中的綜合磁場Bc可表示為

Bc=B+Bn1+Bn2+B3

(3)

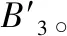
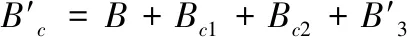
(4)

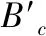
3 仿真系統結構

3.1 仿真系統需求分析

自然基金委重大儀器專項采用低速精檢和高速巡檢的方案實現對高速鋼軌中疲勞接觸裂紋的檢測與評估。為此,一方面需要從理論上深入理解在靜態/準靜態情形下,電場與磁場相互作用的物理基礎理論,實現電磁場的解析計算;另一方面需要深入了解在高速運動狀態下,鋼軌中含RCF裂紋時,動生渦流的分布規律及RCF裂紋對磁場的影響。為此,需要構建動靜態電渦流無損檢測評估仿真系統,為RCF裂紋的定量檢測評估、探頭設計以及試驗驗證提供支持。另一方面,通過理論分析和文獻[18]可看出,對于靜態電磁場,當金屬構件存在裂紋時,其計算精度較高,且計算效率得到大大提升(約為數值計算的30倍),但其計算過程較為復雜、涉及電磁場和數學知識眾多,晦澀難懂。為此有必要通過電渦流檢測評估仿真系統將整個計算過程封裝,降低計算難度,并在保證計算精度的情況下可快速地獲取不同裂紋參數下的磁場。

高速運行下產生的動生渦流可用于鋼軌表面裂紋的快速定量檢測,但目前對運動狀態下動生渦流的分布、電磁場的分布等缺乏直觀認識。雖采用ANSYS Maxwell可實現運動情形下的電磁場仿真,但瞬態分析所需時間長,建模過程復雜,對分析人員的數值建模理論要求較高,為此有必要簡便快捷地可視化展示運動速度和鋼軌疲勞裂紋參數對電磁場分布的影響,幫助設計人員理解運動速度對檢測的影響。

3.2 電渦流無損檢測評估仿真系統體系結構設計

結合3.1節的系統需求分析,構建鋼軌滾動RCF裂紋的電渦流無損檢測評估仿真系統的框架,如圖4所示。

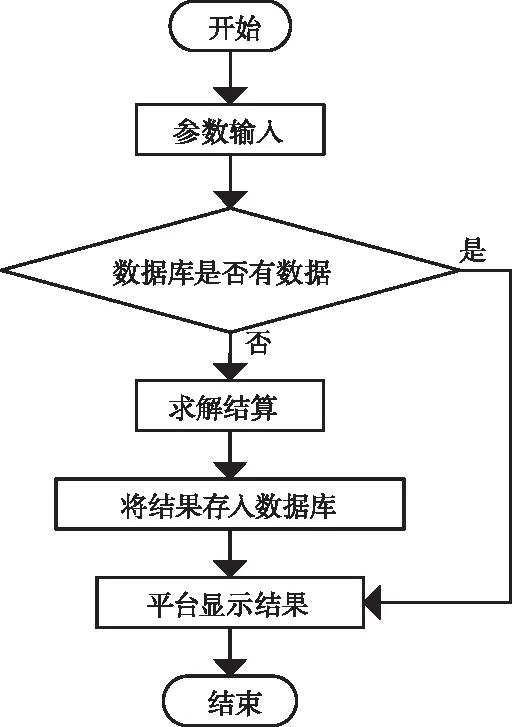
圖4 電渦流無損檢測系統框架

該仿真系統由高速鋼軌RCF裂紋的電磁場靜態計算模塊、直流無損檢測2D仿真模塊和直流無損檢測3D仿真模塊組成,分別實現對含RCF裂紋的電渦流磁場的快速解析計算及高速運行情形下電磁場和動生渦流、速度效應的計算和可視化。該系統不僅可為靜態和動態下鋼軌滾動RCF裂紋定量檢測提供支撐,也可為渦流無損檢測正向/逆向問題研究、傳感器探頭優化設計及試驗驗證提供支持。

3.3 電渦流無損檢測評估仿真系統詳細設計

3.3.1 含RCF裂紋鋼軌靜態電磁場解析計算模塊

基于電渦流無損檢測電磁場解析計算的基礎理論,為實現電磁場的解析計算,文中將曲面鋼軌簡化為平面金屬,將鋼軌中的疲勞接觸裂紋簡化具有矩形截面的直裂紋,利用MATLAB編寫2.2節解析計算函數代碼,實現對磁矢量勢的解析求解。

在實際工程中,鋼軌RCF裂紋參數在一定范圍內變化[16];為克服C#單獨鏈接MATLAB編寫的m文件計算效率低的問題,本文采用數據庫技術將解析計算的磁矢量勢、磁感應強度等保存在數據庫中。當進行解析計算時,根據輸入參數先通過數據庫查詢是否有對應的解析結果,如果有則直接調用,實現解析結果的快速調用與顯示;否則,調用MATLAB編譯的DLL文件計算含RCF裂紋鋼軌電渦流無損檢測電磁場,將解析計算結果保存于數據庫并顯示計算結果。該計算流程如圖5所示。

在C#上調用MATLAB函數時,需先配置MATLAB運行環境變量,保證C#能在path環境變量中找到DLL文件;然后編寫磁矢量勢數值計算求解函數;通過MATLAB的deploytool命令將解析函數生成DLL文件(環境需選擇.NET Assembly環境);創建C#項目導入編譯的DLL文件,根據不同項目功能編寫相應函數,實現在C#平臺上對特征值的求解和鋼軌RCF裂紋模型的解析計算,如圖6所示。

將MATLAB的計算結果存儲于數據庫前需先配置相關的數據源,將數據存儲于指定的數據庫;鏈接建立完成后,執行數值插入的SQL語句;可執行SQL查詢語句查看數據庫調用結果,具體過程如圖7所示。

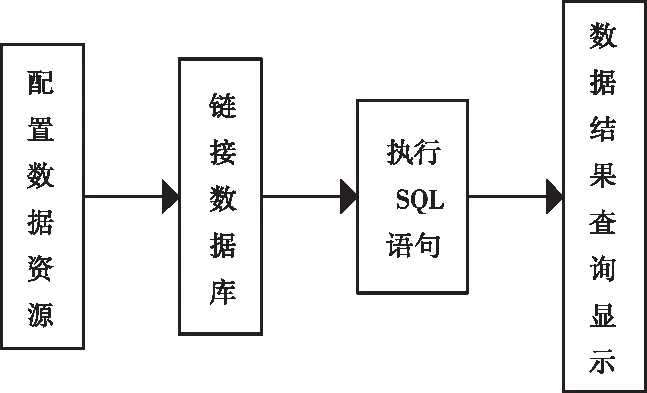
圖7 MATLAB數據存儲于數據庫的過程

3.3.2 高速鋼軌RCF裂紋直流電磁無損檢測2D仿真模塊

對鋼軌滾動疲勞接觸裂紋的動生渦流無損檢測2D仿真是基于ANSYS Maxwell完成的。其中鋼軌RCF裂紋類型及參數如表1所示。為實現對高速運行情況下含裂紋的鋼軌疲勞裂紋的檢測,分析時需設置靜態區域和動態區域,其中探頭和空氣所在區域為靜態區域,鋼軌所在區域為動態區域,如圖8所示。在靜態區域,探頭固定不動,而在動態區域內,鋼軌以速度v沿X軸負向運動。在求解過程中,靜態區域網格不發生變化,而在動態區域內,由于探頭和裂紋的相對位置不斷改變,每個時間步下動態區域內的網格都需重新劃分,且各區域磁場在兩個區域的邊界處實現傳遞,以完成在該時間步下的磁場計算,因此,建模難度較大。為此,本文基于C#的WinForm平臺結合ANSYS Maxwell搭建鋼軌滾動疲勞接觸裂紋電磁場的2D動態仿真模塊。該模塊將復雜建模過程進行封裝,用戶只需輸入模型參數、網格參數、計算參數,就可實現對2D動態磁場仿真,避免仿真中繁瑣的步驟和建模失誤等對計算結果的影響。

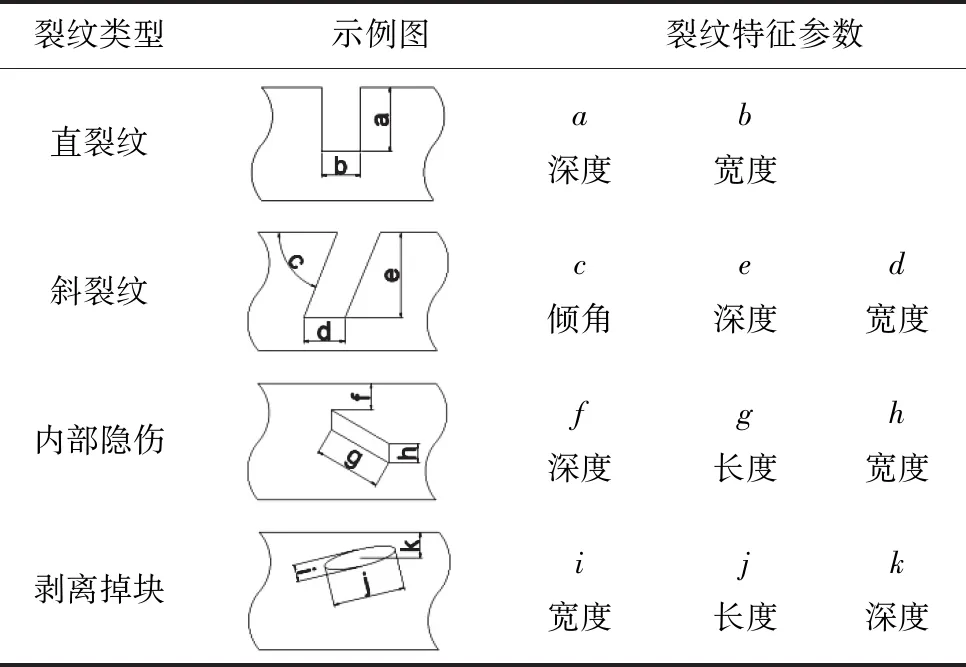
表1 鋼軌RCF裂紋類型及參數

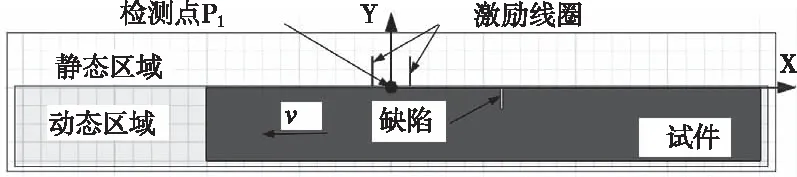
圖8 動靜區域劃分

在該模塊設計中,利用ANSYSMaxwell仿真腳本錄制功能,依次完成模型建立、材料屬性設置、運動設置和網格劃分等功能腳本的錄制。因其腳本文件不能直接用于C#編制,該模塊通過修改其腳本、提取參數并設置為相應控件的輸入值,從而完成腳本文件的編寫過程。該模塊的實現流程如圖9所示。

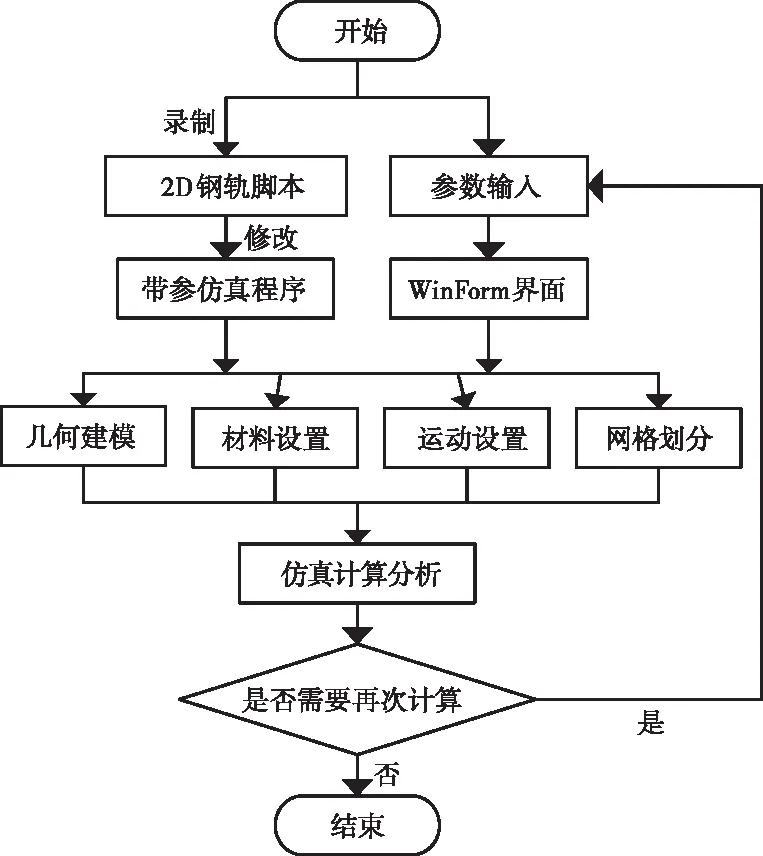
圖9 2D仿真模塊開發流程

3.3.3 高速鋼軌RCF裂紋直流電磁無損檢測3D仿真

在2D仿真平臺雖然實現參數化仿真,但實際的高鐵線路中鋼軌具有復雜的幾何結構,由軌頭、軌腰、軌底構成,如圖10所示。圖中,WH為軌頭高度;b為鋼軌冠狀高度;WT為軌腰高度;HF為接頭夾板安裝面高度;H為鋼軌高度;TF為軌底邊緣厚度;WF為軌底寬度。因此,2D仿真無法全面了解運動情形下含裂紋鋼軌的不同視角的磁場分布,為此設計了鋼軌疲勞裂紋直流電磁無損檢測3D電磁場動態仿真模塊。

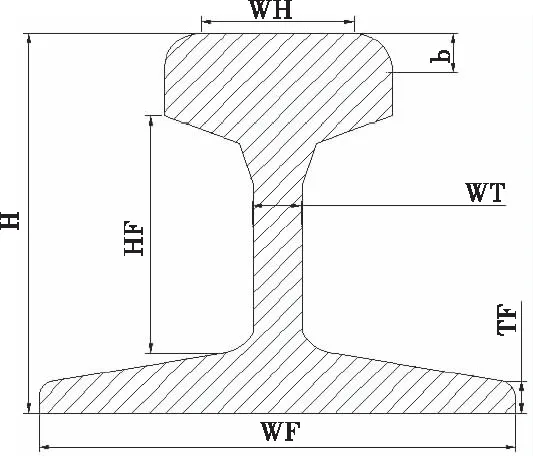
圖10 高速鋼軌幾何結構

雖然鋼軌RCF裂紋直流電磁無損檢測3D仿真模塊也可采用和2D仿真模塊類似的方法建立。但ANSYSMaxwell中直流電磁無損檢測3D仿真相比2D仿真而言,計算耗時太長(在IntelCPU為E5-2630,主頻為2.40Hz,RAM為128GB的64位計算機上大概需要2個月),若要及時獲取3D仿真的電磁場數據并實現數據的可視化,3.3.2小節所述的2D仿真平臺的構建方法已不再適合。為此本文提出一種基于數據庫的鋼軌疲勞裂紋動生渦流場仿真平臺構建方法。該方法分兩步實現:首先建立不同的鋼軌幾何裂紋模型,通過ANSYSMaxwell有限元求解后,將結果數據存儲于數據庫中,如此循環往復,最終建立3D高速鋼軌疲勞裂紋庫,然后在3D仿真平臺上選擇不同裂紋類型跳轉到相應的幾何參數界面,對給定的鋼軌裂紋幾何參數和速度,調用3D高速鋼軌疲勞裂紋庫進行查詢,最終將仿真結果顯示于界面,開發流程如圖11所示。

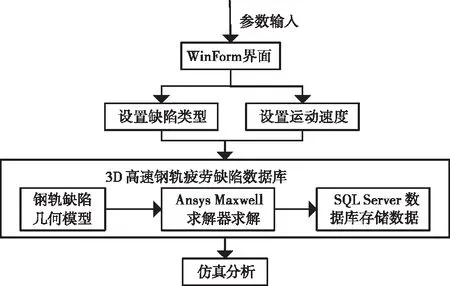
圖11 三維仿真模塊開發流程

在3D仿真平臺構建過程中,通過查看ANSYSMaxwell的仿真文件,發現每一次仿真結果數據量非常大(>200GB),主要為仿真流程產生的數據,分別為動靜態網格劃分文件、磁場分布文件、仿真結果文件等,如果這些文件直接全部存儲于數據庫,會降低結果顯示的及時性。因此通過數據獲取技術,在C#程序里添加SQL查詢語句,將不同速度、不同位置下的磁矢量勢提取存儲于數據庫后,直接調用顯示需要的結果數據,以此解決了存儲數據量大和查詢緩慢的問題。

4 仿真系統開發實例

按照上述基礎理論和開發流程,以某鋼軌為對象對三個模塊進行實例開發。在金屬構件解析計算模塊中,在一定參數范圍內,可根據數學模型提示輸入需計算的參數裂紋參數,點擊計算按鈕完成計算,并將磁場計算結果存儲并顯示,如圖12所示。鋼軌疲勞裂紋無損檢測2D仿真模塊參照幾何模型和運動模型參數化的流程建模、仿真后,通過結果顯示按鈕可獲得仿真結果,從結果可知裂紋位置并實現對不同參數下的計算結果做對比分析,如圖13所示。鋼軌RCF裂紋無損檢測3D仿真模塊中,首先選擇裂紋類型,然后輸入裂紋參數、線圈參數、激勵參數等,并將這些輸入參數作為索引條件,通過調用數據庫,將存儲的數據在界面上動態顯示,可實時查看不同時刻仿真結果,如圖14所示。

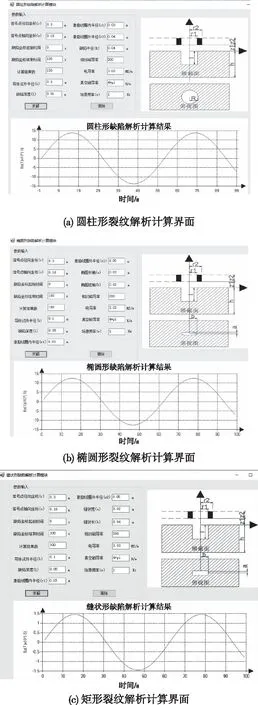
圖12 金屬構件解析計算模塊開發實例

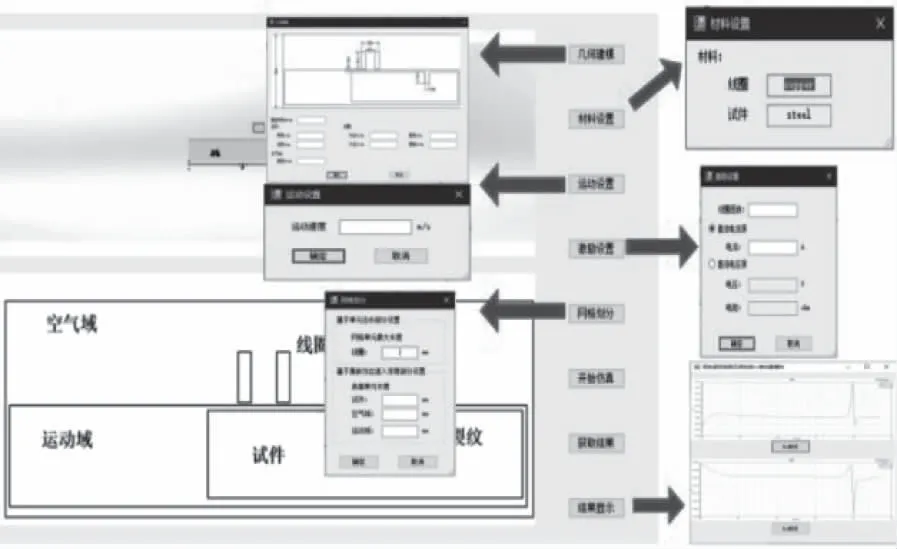
圖13 鋼軌RCF裂紋無損檢測2D仿真模塊界面

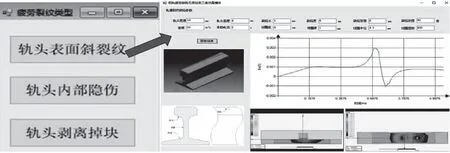
圖14 鋼軌RCF裂紋無損檢測3D仿真模塊

5 仿真系統開發實例

5.1 靜態裂紋參數對電渦流磁感應強度的影響

將鋼軌矩形裂紋深度設定為2mm、寬度設定為2mm時,分別設置矩形裂紋長度為2mm、4mm、6mm、8mm、10mm和12mm時,采用金屬構件解析計算模塊分析裂紋長度與Bz峰值的關系,如圖15(a)所示。將鋼軌裂紋深度設定為2mm、長度設定為2mm時,設置矩形裂紋寬度分別為2mm、4mm、6mm、8mm、10mm和12mm時,分析鋼軌傷損的矩形裂紋寬度與Bz峰值的關系,如圖15(b)所示。

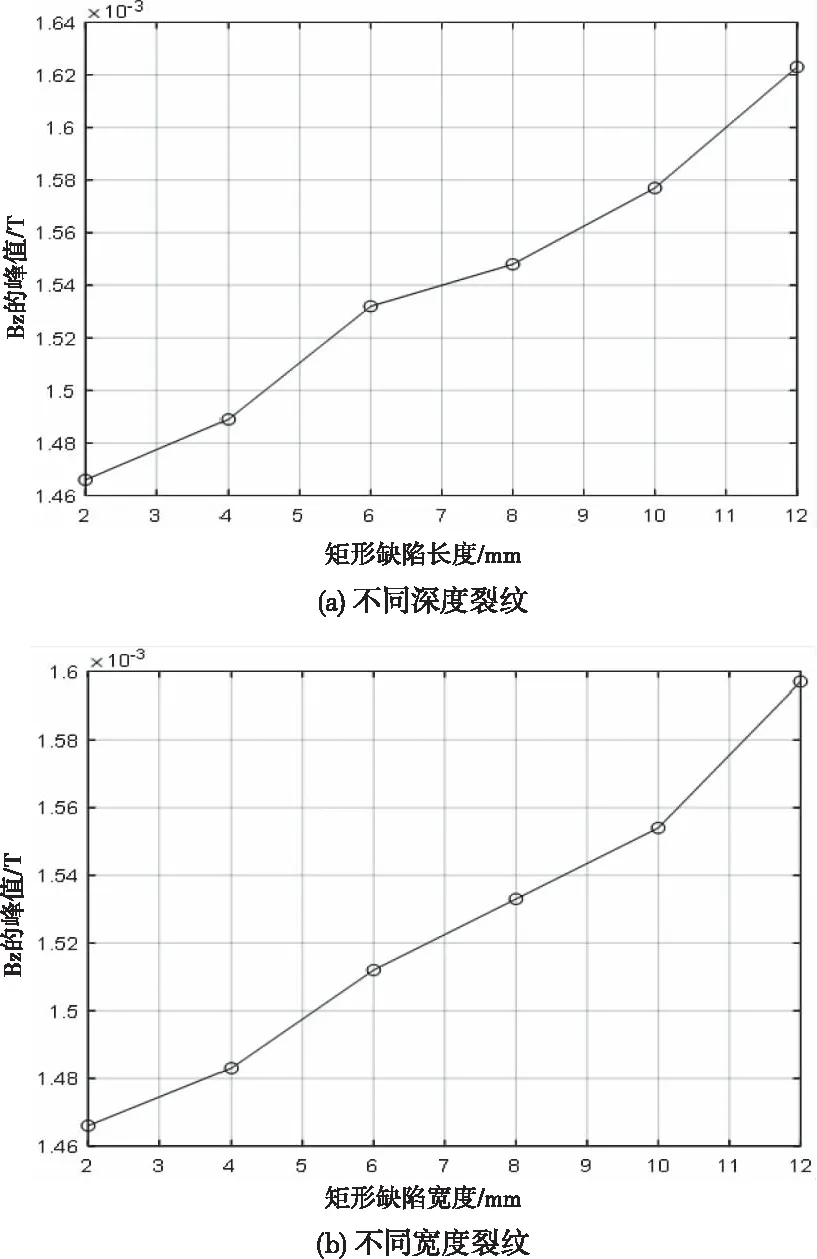
圖15 矩形裂紋與Bz峰值的關系曲線

從圖15(a)中可看出,當鋼軌傷損中直裂紋深度為2mm、寬度為2mm時,隨矩形裂紋長度增加磁感應強度Bz峰值隨之增加。從圖15(b)中可看出,當鋼軌傷損的矩形裂紋深度為2mm、長度為2mm時,隨矩形裂紋寬度增加,磁感應強度Bz的峰值也隨之增加。

5.2 2D高速鋼軌RCF裂紋對電渦流磁感應強度的影響

采用仿真系統中高速運行下鋼軌RCF裂紋2D和3D仿真模塊,可實現對動生渦流磁場分布與鋼軌RCF裂紋深度與寬度的定量分析。當直流激勵電壓為5V,提離距離為0.5mm,線圈內徑、外徑和高度分別為10mm、10.5mm和8mm,線圈匝數為200匝時,得到檢測速度為5m/s和20m/s時鋼軌內部動生渦流分布圖,如圖16所示。可看出,隨檢測速度增加,鋼軌中動生渦流越強,且趨膚效應和拖影效應越明顯。

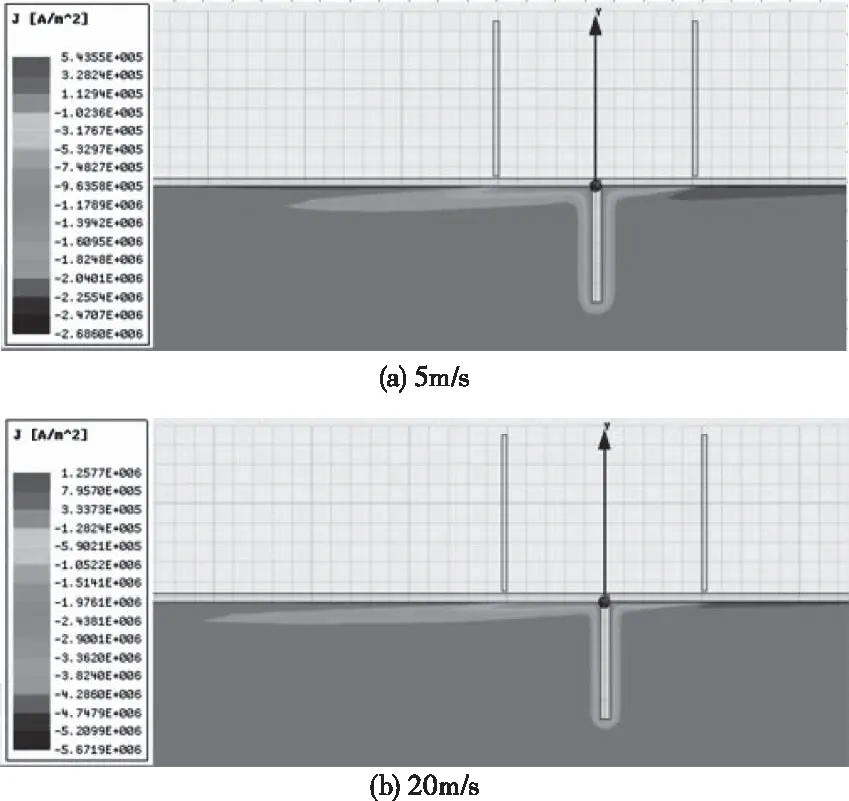
圖16 動生渦流分布圖

當檢測速度為20m/s時,裂紋寬度為0.5mm,深度分別為1mm、2mm、4mm、5mm和6mm時,可得到P1點處(如圖9所示)磁感應強度水平(X軸)分量Bx和豎直(Y軸)分量By值,裂紋深度與Bx、By關系曲線如圖17所示。當裂紋深度為6mm,寬度為0.5mm、1.0mm、1.5mm和2.0mm時,同樣可獲取P1點處的Bx和By值,得到如圖18所示裂紋寬度與磁感應強度的關系曲線。

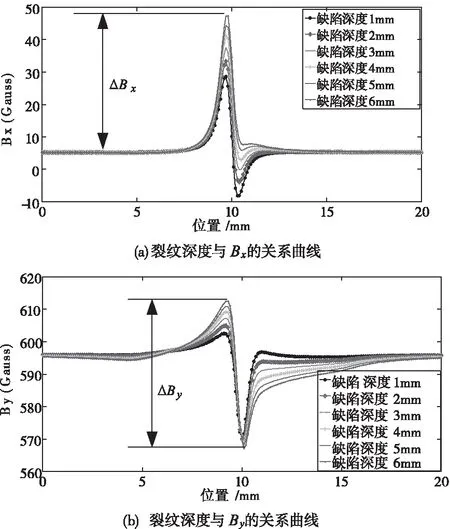
圖17 不同裂紋深度與磁感應強度的關系曲線

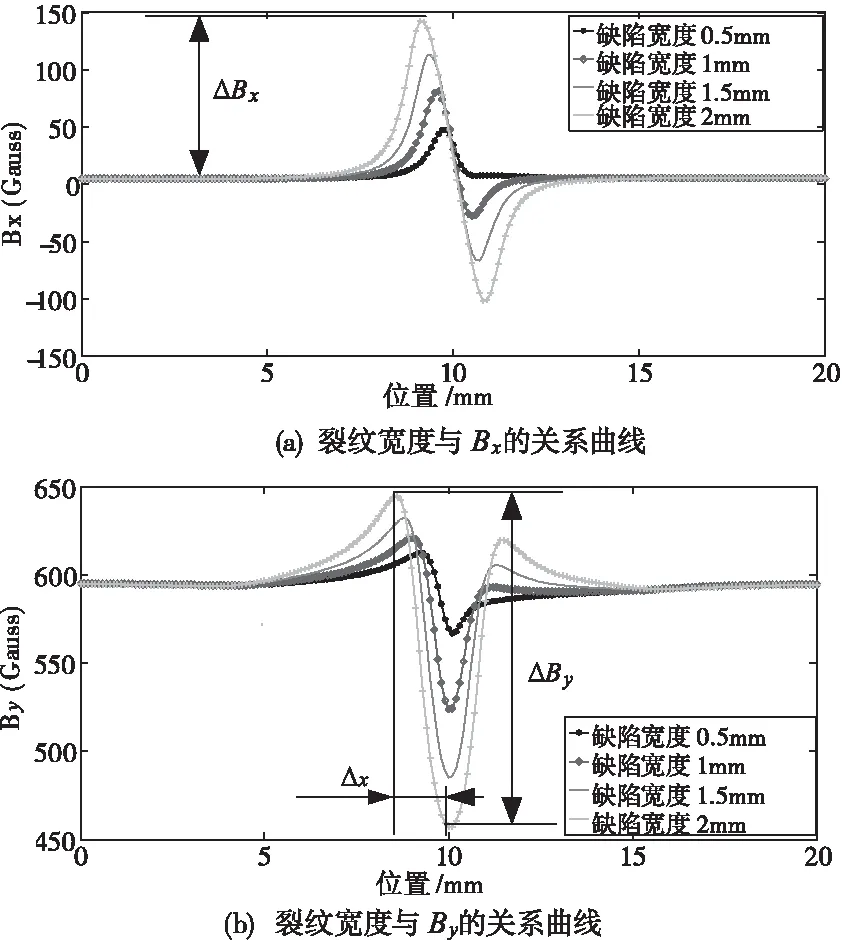
圖18 不同裂紋寬度與磁感應強度的關系曲線

從圖17可觀察到,隨裂紋深度增加,Bx峰值隨之增加,而谷值逐漸減小并消失;By峰值與谷值的絕對值(即△Bx)增加。但隨裂紋深度增加,By峰值和谷值的絕對值(即△By)變化趨勢均減緩。因此,可通過磁感應強度Bx、By峰值和谷值對裂紋深度進行識別。從圖18中同樣可得出,隨裂紋寬度增加,Bx和By峰值增大,By谷值的絕對值也增大。同時,如圖18(b)所示,隨著裂紋寬度的增加,By的峰值與谷值之間的距離△x增加。因此可通過Bx、By峰值和谷值對裂紋的深度和寬度進行識別。

5.3 3D高速鋼軌RCF裂紋對電渦流磁感應強度的影響

為分析不同鋼軌裂紋對磁感應強度的影響。設置巡檢速度為20m/s,裂紋寬度為0.8mm,裂紋深度分別為0.5mm、1.0mm、1.5mm、2.0mm時,研究磁感應強度峰值X方向和Y方向的變化情況,其X方向、Y方向的磁感應強度的峰值隨裂紋深度的變化曲線分別如圖19(a)和19(b)所示。

從圖19(a)的X方向磁感應強度峰值變化曲線可以看出,隨著裂紋深度的增加,檢測到的磁感應強度增強。從圖19(b)的Y方向磁感應強度峰值變化曲線可以看出,隨著裂紋深度的增加,檢測到的磁感應強度增強。進一步分析對比X方向和Y方向的磁感應強度峰值的相對大小,發現X方向的磁感應強度峰值小于Y方向的磁感應強度峰值。

6 總結

本文設計開發了適用于鋼軌RCF裂紋電渦流檢測評估仿真系統,通過該系統可實現渦流無損檢測電磁場的快速解析計算,也可對運動狀態下鋼軌中滾動接觸疲勞裂紋的特征參數和動態電磁場的關系進行深入研究,為提出鋼軌滾動接觸疲勞裂紋的定量、快速無損檢測方法提供支撐。此外,該系統在C#平臺上聯合MATLAB、ANSYSMaxwell和數據庫技術,將靜態電磁場的晦澀難懂的解析計算過程和動態電磁場的復雜建模過程進行封裝,在降低系統的使用難度的同時,可實現含不同RCF裂紋的高速鋼軌電磁場的快速計算和快速可視化。

因此該系統不僅可用于提出鋼軌RCF裂紋的電渦流無損定量檢測方法、正向逆向問題研究、探頭優化設計和試驗驗證,也為進一步構建鋼軌RCF裂紋的無損快速定量化檢測系統對應的數字孿生系統奠定基礎。