平面向量綜合問題分類導析

陳元菊

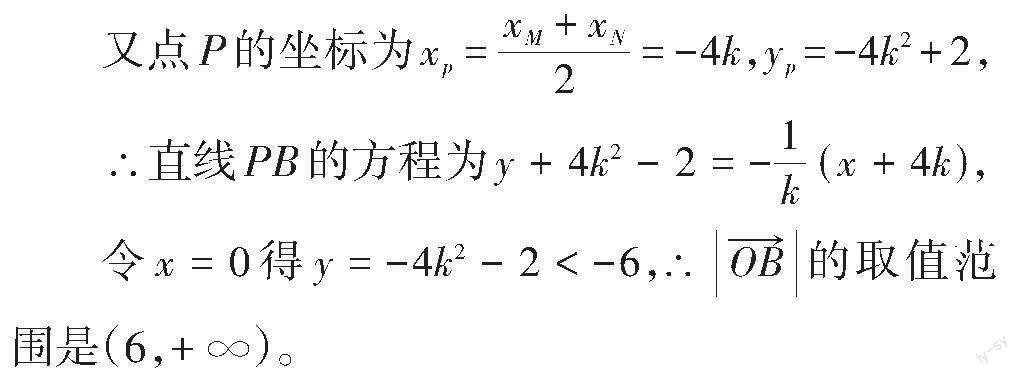
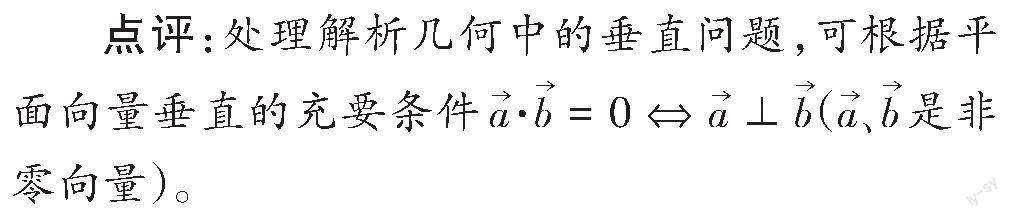
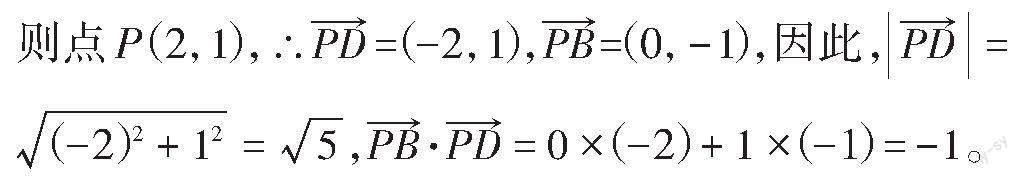
［摘 要］平面向量是高中數學的重要概念與工具。平面向量融數、形于一體，具有代數與幾何的雙重身份。平面向量既體現“形”的直觀特征，又體現“數”的運算特征，因而平面向量是聯系幾何圖形和代數運算的紐帶，平面向量還是數學學科知識交匯和聯系多項內容的媒介。平面向量與代數、幾何以及三角都有著千絲萬縷的聯系，是高中數學眾多知識網絡中的交匯點。平面向量的引入，能大大拓寬學生解決數學問題的思路，為高考試題的命制提供了一個相對豐富的脈絡。在高考中，平面向量常與解三角形、三角函數、平面幾何、解析幾何等知識進行綜合考查。鑒于平面向量的重要作用，文章重點分類探析平面向量綜合問題，以期幫助數學教師了解平面向量在高考中題型的變化和發展趨勢。

［關鍵詞］平面向量；綜合問題；解三角形；三角函數；平面幾何；解析幾何

［中圖分類號］? ? G633.6? ? ? ? ［文獻標識碼］? ? A? ? ? ? ［文章編號］? ? 1674-6058（2023）17-0017-04

高中數學知識縱橫聯系、互相滲透。高考數學試題突出考查知識的全面性和綜合性，強調知識的交匯和融合，試題往往設計在知識網絡的交匯處，特別注重考查學生解決問題的能力。平面向量融數、形于一體，具有代數和幾何的雙重身份，是一種溝通代數、幾何與三角的重要工具。下面筆者以例題解析的形式，分別探討平面向量與其他知識的綜合，以期幫助數學一線教師了解平面向量在高考中題型的變化和發展趨勢。

一、平面向量與解三角形的綜合

平面向量與解三角形的綜合體現在：平面向量的幾何意義與三角形幾何特征的聯結，三角形的邊長向量描述為向量的模，三角形內角（或內角的補角）的向量描述為向量的夾角，平面向量的加法、減法、數量積運算可溝通三角形邊、角運算，正弦定理、余弦定理、三角形面積公式也都和平面向量運算有著直接或間接的聯系。

平面向量與解三角形的綜合知識：

在[△ABC]中，內角[A、B、C]所對的邊分別為[a、b、c]，[D]是邊[BC]的中點，則有：

∴[2·BC·（-cosB）=1]，∴[2·BC·cosB=-1] （1）

由三角形的余弦定理可得

[AC2=AB2+BC2-2AB·BC·cosB]

∴[32=22+BC2-4·BC·cosB]? （2）

點評：在這個問題中平面向量數量積運算發揮了牽線搭橋的作用，利用平面向量數量積運算建立起了三角形的邊長與內角之間的數量關系，把問題由向量計算轉化為三角形的邊長與內角計算。此題余弦定理的應用也很關鍵，進一步溝通了三角形邊和內角的數量關系，在求解過程中運用了方程思想。

點評：此題對學生思維能力的考查力度大，用常規方法去解題無從下手。由點[D]是邊[AC]的中點聯想到三角形中線向量的性質，向量的平方等于向量模的平方，而向量的模即是三角形中有關線段的長度。此題解題過程中平面向量的切入，起到了“一點突破，全線貫通”的作用，特別是在計算過程中，平面向量數量積貫通了三角形的邊、角的關系。平面向量運算與三角形邊、角運算高度契合，可以體會到平面向量與解三角形的綜合，給了這樣的問題一個創新思路。

平面向量與解三角形的綜合規律總結：

1.以平面向量為載體，交叉綜合解三角形；

2.以三角形為載體，利用平面向量數量積和模的概念等脫去平面向量的“外衣”，轉化為三角形的邊、角問題。

二、平面向量與三角函數的綜合

平面向量與三角函數的綜合也是高考的重點和熱點，平面向量與三角函數綜合問題一般是以三角函數為背景，根據平面向量的加法、減法、數乘向量、數量積等運算性質，將平面向量問題轉化為三角函數的相關問題來解答。此類問題往往融合向量的數量積、向量的模 、向量的坐標表示以及三角函數的性質、公式、化簡、最值，具有覆蓋面廣、綜合性強、解法靈活的特點。

平面向量與三角函數的綜合常涉及向量的坐標運算：

點評：此類問題中平面向量本質上只是作為知識背景或載體的形式出現，考查重點實際為三角函數，解題的關鍵是恰當地實施三角函數知識與平面向量知識的轉化。

平面向量與三角函數的綜合規律總結：

題目條件給出平面向量的坐標中包含有三角函數的形式，一般通過平面向量平行、垂直、向量模、數量積的運算，將平面向量轉化為三角函數中的數量關系，然后再結合三角函數的圖象與性質進行求解。

三、平面向量與平面幾何的綜合

平面向量與平面幾何的綜合問題的解題關鍵是：根據平面向量在平面圖形中的幾何意義，將平面幾何的問題化歸為平面向量的問題來處理，或者將平面向量的問題化歸為平面幾何的問題來處理。

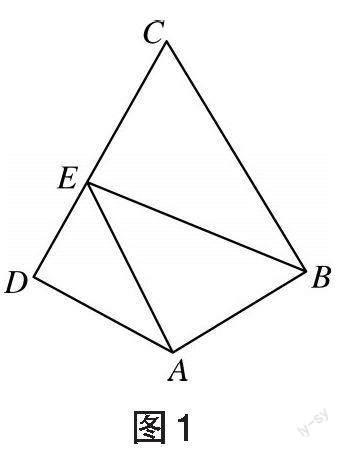
平面向量與平面幾何的綜合知識：

點評：結合平面向量共線定理，把幾何問題中三點共線轉換成向量共線，參數[t]的引入，把平面向量數量積轉化為關于[t]的函數，利用函數性質可求得最小值。

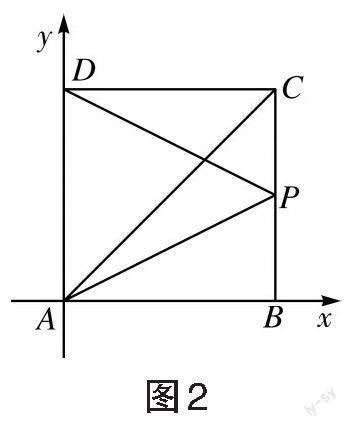
點評：解決涉及平面幾何圖形的向量運算問題常有兩種方法：一是定義法，二是坐標法。定義法即根據平面向量的幾何性質，建立起平面幾何與平面向量的關系，用平面向量表示問題中的有關幾何元素，如平面向量的三角形加法法則、平行四邊形加法法則、三角形減法法則、數量積的定義，將平面幾何問題轉化為平面向量問題。坐標法即把平面幾何圖形構造到平面直角坐標系中，賦予圖形中有關點的坐標、有關平面向量的坐標，一旦引入向量的坐標表示，向量的加減、向量的模、向量的數量積等運算，就都可以轉化為代數運算，這樣就可以將形與數緊密結合在一起。對于長方形、正方形、直角三角形中的向量運算，可以考慮建立直角坐標系，用平面向量的坐標法解決，把幾何關系“翻譯”成向量坐標運算，這樣可以大大優化解題過程。

平面向量與平面幾何的綜合規律總結：

平面向量與平面幾何的綜合問題考查平面幾何問題中向量知識的運用，常以平面幾何的基本圖形（如三角形、四邊形等）為背景，從平面向量的“數”和“形”兩個方面特征入手進行思考。如果重點考查平面向量的“數”的特點，就要從平面向量的代數運算上去突破，可以建立適當的平面直角坐標系，設點坐標，進而求出平面向量的坐標，再進行向量運算，把問題轉化為代數問題。如果重點考查平面向量的“形”的特點，就要從平面向量的幾何意義上去突破，這就需要選擇兩個合適的向量作基底，根據平面向量的幾何意義，將問題轉化為平面幾何中“形”的問題。

四、平面向量與解析幾何的綜合

從“形”的角度看，平面向量是有方向的線段；從“數”的角度看，平面向量的坐標可以用它的起點和終點的坐標來表示；在思想方法上，平面向量和解析幾何保持高度一致，所以平面向量和解析幾何有著天然的內在聯系。平面向量的形式和語言經常出現在解析幾何問題中，涉及平行（共線）、垂直、夾角、長度、軌跡等問題的處理，解決問題的基本思路有兩種：一是利用平面向量坐標表示，把幾何推理、證明轉化為代數運算，即把“形”轉化為“數”；二是將平面向量代數運算轉化為平面圖形的位置關系，即把“數”轉化為“形”。

平面向量與解析幾何的綜合：

1.以平面向量為載體，在平面向量與解析幾何知識層面上進行整合，幾何元素之間的平行、垂直、共線等關系運用平面向量的語言來描述和解析，綜合考查學生對平面向量的加法、減法，平面向量的數量積運算及其幾何意義，以及對圓錐曲線的定義和性質的理解。

2.以平面向量作為工具，在平面向量與解析幾何應用層面上進行整合，考查學生對平面向量的概念、加減運算幾何意義、坐標表示、數量積幾何意義、平面向量共線定理的理解。另外，圓錐曲線的標準方程及有關角度、長度、軌跡等問題，都可應用平面向量數量積的運算來解決。

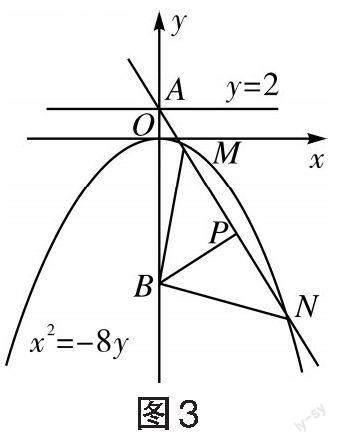
A. 外心 B. 內心 C. 重心 D. 垂心

解析：∵拋物線的解析式為[x2=-8y]，準線為[y=2]，∴[A（0，2）]，

設[MN]的中點為[P]，由向量加法法則得

∴[PB]垂直平分線段[MN]。

設直線[MN]的方程為[y=kx+2]，與[x2=-8y] 聯立消去[y]，得[x2+8kx+16=0]，由[Δ>0?64k2-4×16>0?k2>1]，

點評：處理解析幾何中的垂直問題，可根據平面向量垂直的充要條件[a·b=0?a⊥b]（[a、b]是非零向量）。

平面向量與解析幾何的綜合規律總結：

1.解析幾何中復雜的推理、位置關系可根據平面向量的幾何意義，運用坐標進行轉化，通過向量坐標演化成簡單的代數運算，轉化途徑主要有兩種：一是利用平面向量數量積的公式和性質；二是利用平面向量平行或垂直的充要條件。

2.某些解析幾何問題若用常規方法去解決，會因為運算繁雜而導致失敗，不妨利用平面向量作形與數的轉化，即把平面向量作為工具去探索圓錐曲線的標準方程和幾何性質，回歸到解析幾何的基本思想方法，這樣會大大簡化解題過程。

綜上可知，平面向量與解三角形、三角函數、平面幾何、解析幾何的綜合，凸顯了平面向量的交匯性和工具性。平面向量與代數、幾何、三角都具有相當高的融合性，平面向量使整個高中數學教材體系更富有活力，平面向量為學生解決問題提供了一種有效捷徑。用平面向量作為工具處理有關問題，簡練優美，極具優越性。教師應引導學生理解平面向量的兩個核心特征：幾何特征和代數特征，把握平面向量與其他知識的內在聯系，進行平面向量與其他知識間的綜合，樹立應用平面向量解決問題的意識。

［? ?參? ?考? ?文? ?獻? ?］

［1］? 余華安.例談平面向量在解析幾何問題中的應用［J］.中小學數學（高中版），2008（Z1）：64-66.

［2］? 王紅革，許志勇，沈婕.高考中“平面向量”測試對教學的反撥效應分析：以普通高考（天津卷）為例［J］.考試研究，2014（2）：3-9.

［3］? 干亞清.平面向量在解析幾何中的應用［J］.高中數學教與學，2011（14）：46-47，40.

［4］? 伊建軍.平面向量題型與高考走勢［J］.中學教研（數學），2008（2）：26-28.

［5］? 陳利民.平面向量及其運用［J］.中學教研（數學），2013（2）：1-4.