抗滑樁不同參數取值對邊坡穩定性的影響研究

王濟滄 黃康娜 桑慶云

（1濟南城市建設集團有限公司，山東 濟南 250000；2濟南城建集團有限公司，山東 濟南 250000）

0 引言

在邊坡治理工程中，常常選取經濟性好、支護效果好、施工速度快、抗滑能力強的支護措施，而抗滑樁具有以上優點，因此在實際施工中得到了廣泛應用。但是每個邊坡工程的地質條件不同，抗滑樁的參數選取也不相同。目前普遍采用極限平衡法進行參數選取分析，而極限平衡法也有弊端。極限平衡法雖然假設了樁在支護情況下的受力及滑動變形情況，但并沒有體現樁與土之間的相互作用和邊坡變形規律[1-2]。利用基于有限元法或者有限差分法的數值分析，可以為研究樁身參數對邊坡穩定性的影響提供有效的研究手段[3]。

楊光華等[4]采用FLAC3D軟件模擬抗滑樁不同加固位置及尺寸，進而分析邊坡的安全性；Won 等[5]采用極限平衡法和FLAC3D相結合的方式，對邊坡的穩定性系數以及樁體的力學性能參數進行了研究，并且探討了邊坡的穩定性；王聰聰等[6]對抗滑樁支護加固邊坡的效果進行了研究，分析了抗滑樁的最優工況；劉怡林[7]等利用數值模擬軟件FLAC3D對不同工況進行了模擬，提出了抗滑樁支護參數的優化方案；戴自航等[8]結合工程實際情況，研究了在施工中抗滑樁的最佳設計方案。在抗滑樁作為支護方式的研究中，主要是針對抗滑樁的各個參數進行優化，其次是探討邊坡的安全系數，但很少考慮樁與土的相互作用機理，也無法體現抗滑樁的內力變化規律以及樁的變形變位規律。由此可知，目前的研究缺少對抗滑樁綜合參數的研究，往往根據施工經驗確定樁的彈性模量、樁身長度、布樁位置等參數，這樣的取值通常比較保守，也缺乏科學性，存在浪費資源的情況。

基于此，本文采用FLAC3D軟件進行數值模擬，分別研究抗滑樁彈性模量、加固位置及樁身長度三個參數的變化對邊坡穩定性的影響。

1 理論計算模型分析

在FLAC3D軟件中采用樁單元進行抗滑樁的模擬，可以獲得準確的計算數據。抗滑樁理論計算模型如圖1所示。樁-土之間的相互作用通過模擬法線方向和切線方向的耦合彈簧數值計算，耦合彈簧屬于滑塊與非線性彈簧的組合體，能夠實現實體單元與模擬樁單元網格之間的彎矩與力的相互傳遞。

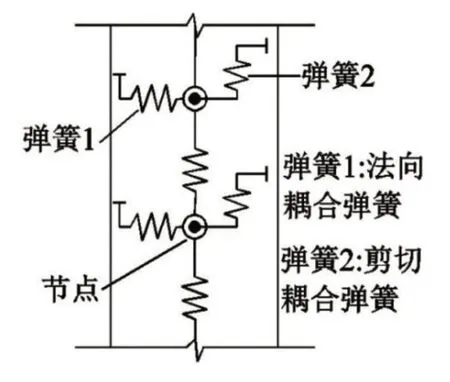
圖1 抗滑樁力學計算模型

計算過程中，圍巖網格和樁單元節點之間產生相對位移從而產生剪力的計算公式如下：

式中：FS——剪切方向上非線性彈簧產生的剪切力；

L——模擬單元有效單元的長度；

css——剪切連接彈簧的剪切剛度；

usi——抗滑樁的軸向位移；

usm——巖土滑動面的軸向位移。

抗滑樁法線方向非線性彈簧的法向力計算式如下：

式中：Fn——法線方向非線性耦合彈簧產生的法向力；

L——模擬單元有效單元長度；

cns——法線方向非線性耦合彈簧的法向剛度；

uni——垂直于抗滑樁軸向的樁的位移；

unm——垂直于樁軸線方向介質面的位移。

2 數值計算模型建立與參數選取

按平面應變建立邊坡計算模型，巖土體變形采用Mohr-Coulomb準則，利用強度折減法計算邊坡穩定性系數，將是否收斂作為邊坡失穩的判據。利用自編的FISH語言提取滑動面數據，將滑動面上各點的位移量化。

建模分析計算圖如圖2 所示，露天邊坡的傾斜角度較大，夾角假設為60°，屬于高陡邊坡。根據實際工程的監測數據顯示，花崗質碎裂巖與黃鐵絹英巖化花崗巖相交的平面易產生相對滑移，從而作為重點研究對象。抗滑樁的設計樁徑為2000mm，計算過程中采用的樁長分別為12m、16m、20m、24m、28m、32m 和36m。圖2 所示的LX表示為抗滑樁加固位置到坡腳的距離，取值為（6,48），其中，x表示步距，大小為6m；L表示邊坡的水平投影距離長度，為48m。巖土參數和樁身參數取值如表1所示。

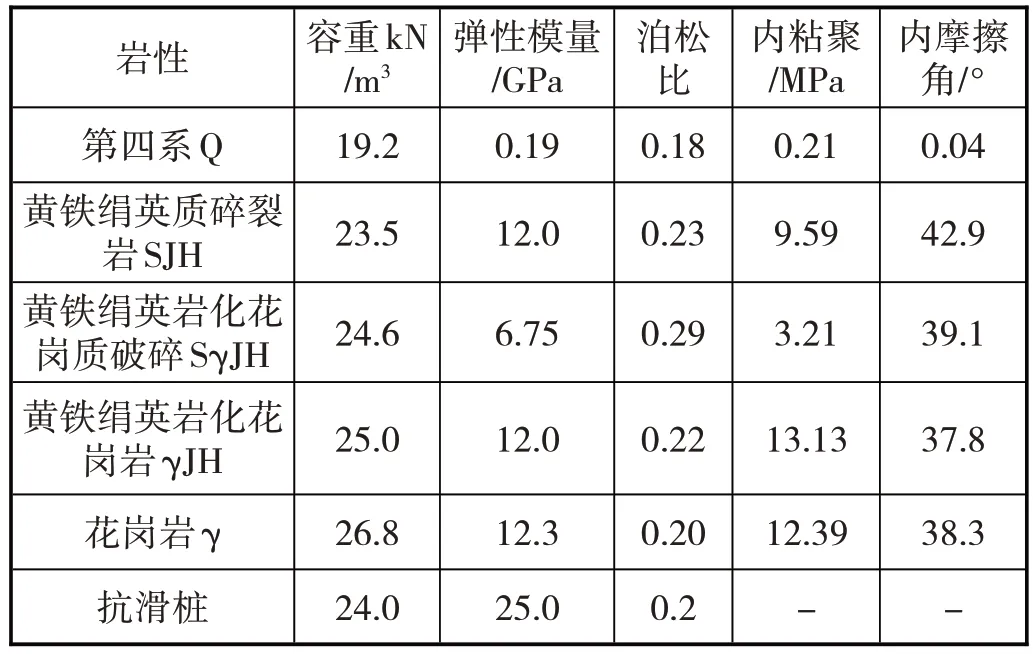
表1 巖土參數與樁身參數

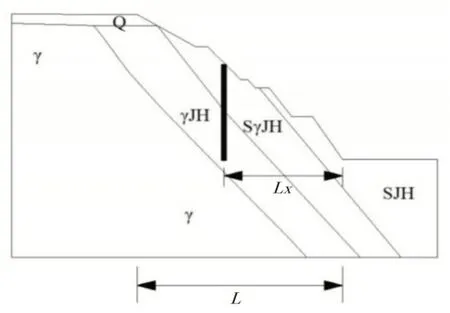
圖2 數值計算模型示意圖

3 抗滑樁不同參數取值對邊坡穩定性影響分析

3.1 抗滑樁不同加固位置的影響

抗滑樁加固邊坡時，加固位置對邊坡穩定性也有影響。如圖3 所示，當抗滑樁的樁長取值較小時，抗滑樁選取的加固位置對邊坡的穩定性影響不大。假設抗滑樁的選取位置在坡腳及其附近時，抗滑樁的加固效果并不明顯。當設樁位置到坡腳的水平距離與邊坡的水平投影距離比值增大時，抗滑樁對邊坡的加固效果越明顯，邊坡的穩定性系數越好。樁長不同，其最優加固位置也不盡相同。當樁長為28m 時，穩定性系數趨于穩定。當樁長為30m 時，最優的加固位置不是在邊坡中部，而在位置5，此時抗滑樁加固邊坡的效果最好。

圖3 抗滑樁不同加固位置）和樁身長度與邊坡穩定系數的關系

3.2 抗滑樁不同樁身長度的影響

由圖3 可知，曲線1 和曲線2 為平緩曲線，說明此時樁長對邊坡的穩定系數影響不大。在這兩個位置，邊坡的穩定性系數穩定在1.0 附近，此時邊坡不穩定。在位置L3、L7、L8，隨著樁長的增加，穩定性系數也隨之增大，在位置L7較為明顯。此時抗滑樁的樁長越大，邊坡穩定性系數也越大，邊坡越穩定。在位置L5、L6、L4時，上述現象愈發明顯，但無論在哪個位置，樁長大于28m 時，邊坡穩定性系數均趨于穩定，此時增加樁長對邊坡的穩定性影響較小，反而增加成本，浪費資源。邊坡穩定系數隨著樁長的增加只是略有增加，甚至趨于穩定。也就是說此時樁長增加，抗滑樁穩定系數不再有明顯變化，此時增加樁長不再明顯影響邊坡的穩定性。推斷抗滑樁的有效嵌固深度就在邊坡穩定系數反彎點處，根據模擬結果可知，此時抗滑樁的樁長為最經濟樁長，即在L5位置有最大的嵌固深度。

3.3 抗滑樁不同彈性模量的影響

在位置L5，最優樁長值為32m，此時邊坡穩定性系數接近極值，增加樁長對加固效果并不明顯，優化樁的彈性模量繼續進行邊坡穩定性分析，所得結果如圖4所示。

圖4 抗滑樁不同彈性模量與邊坡穩定系數的關系圖

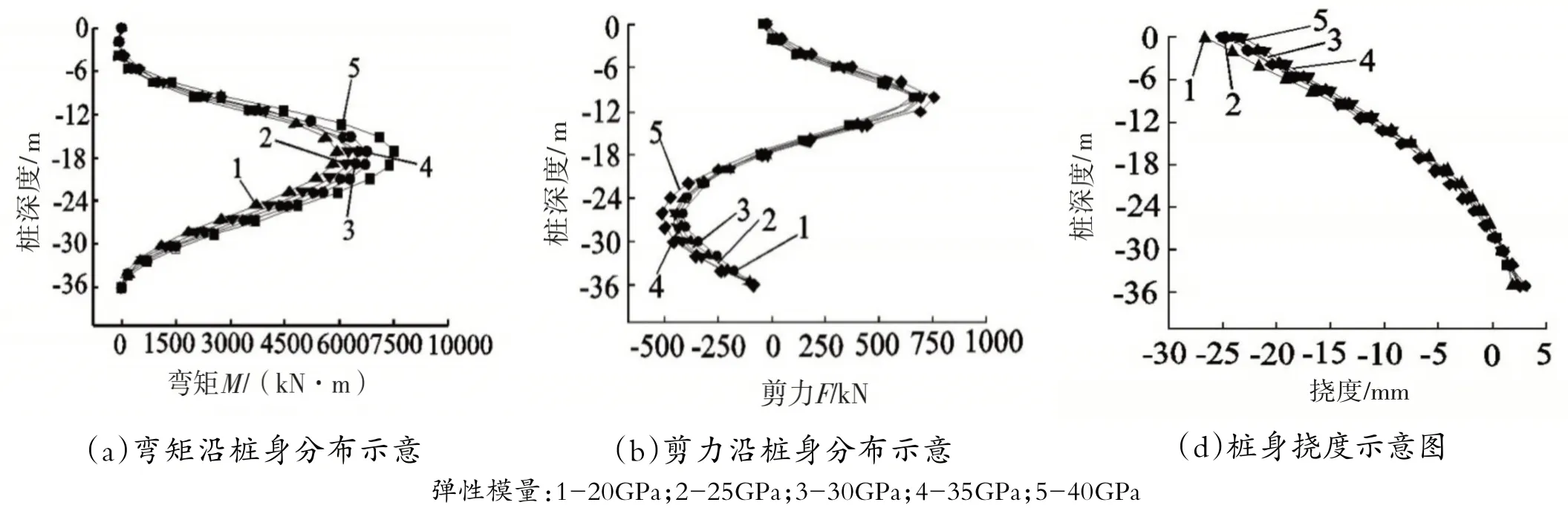
圖6 不同彈性模量抗滑樁變矩、剪力、撓度分布示意圖

由圖4 可知，增大彈性模量并不能使穩定性系數有明顯增加，調整彈性模量，穩定系數變化僅為1.15%。且彈性模量在20~40GPa 之間取值時，穩定性系數可以視為不變，因此在此區間取值，彈性模量對邊坡的穩定性沒有影響。

3.4 抗滑樁不同彈性模量對樁身內力和變位的影響

將抗滑樁的彈性模量作為自變量，其余參數保持不變進行模擬研究，得到采用不同彈性模量的情況下，抗滑樁不同長度處的彎矩、剪力變化規律以及不同樁長的撓度變化規律，模擬結果如圖5所示。

由圖5 可以看出，樁身彈性模量不斷增大，抗滑樁的樁身彎矩及剪力也隨之增大。埋深36m 的樁，在埋深約為-18m 時的彎矩最大。充分對比分析模擬結果得出，樁身內力的變化并不顯著，彎矩的相對誤差僅占18.6%，樁頂撓度的誤差僅有3.5mm，并且隨著樁深度的不斷增大，不同彈性模型工況下其樁撓度也基本一致，曲線基本重合，說明彈性模量的影響不大。

綜合對三個主要特征指數（抗滑樁變位、邊坡穩定性系數、抗滑樁樁身內力）進行分析后發現：雖然樁身變位隨著抗滑樁彈性模量增大而減小，但效果并不明顯，在施工過程中收效甚微，在實際施工過程中，一般采用更高強度的混凝土和受力鋼筋來提高彈性模量，這會大大提高抗滑樁的施工成本及工期，造成資源浪費。因此，在工程設計階段，只需根據工程實際合理確定抗滑樁彈性模量，綜合考慮工程成本、施工進度及支護效果，一般不采用通過增加抗滑樁彈性模量來提高邊坡穩定性系數的方法。

4 結束語

綜上所述，本文采用數值模擬的方法，研究了抗滑樁在選取不同參數時的邊坡穩定情況，得到如下結論：抗滑樁布置在越靠近坡腳的位置，邊坡穩定性越差，且樁長的增加或減小對邊坡穩定性影響不大；抗滑樁樁長小于24m 時，抗滑樁樁位對邊坡穩定性影響同樣不大，當樁長大于24m時，合理布設抗滑樁的位置對提高邊坡穩定性有顯著的效果；單純提高抗滑樁的彈性模量并不能有效增大邊坡穩定系數，但抗滑樁的位移有一定減小；在實際工程中利用抗滑樁加固邊坡時，根據工程實際合理確定抗滑樁的最優彈性模量即可。