融合卡爾曼改進小波的姿態傳感器濾波方法

王靜靜，秦 剛，李騰

（西安工業大學 電子信息工程學院，西安 710021）

XGZT-XXX 型姿態傳感器為西安工業大學自主研發，由MEMS 加速度計、MEMS 陀螺儀與MEMS傾角傳感器組成，該傳感器具有體積小、成本低、功耗低等優點。但由于MEMS 陀螺儀自身輸出噪聲大，且在實驗過程中受不可避免的各種復雜的振動、干擾激勵（如實驗過程中人員的走動、安放不穩引起抖動等），為了提高系統測量精度，需要對其進行降噪處理。

對慣性器件濾波處理，有經典濾波器和現代濾波器，慣性器件的噪聲與信號通常是相互重疊，不適合使用經典濾波器（IIR、FIR），可根據信號和噪聲的統計特性，利用數理統計方法進行估計，即現代濾波器[1]。現代濾波器中常用的方法有卡爾曼濾波、經驗模態分解（empirical mode decomposition，EMD）、小波閾值去噪等[2]。文獻[3]建立了時間序列模型引入卡爾曼進行濾波處理，但缺乏自適應性，長時間會導致濾波發散。文獻[4]中將卡爾曼與小波進行了融合，并且對卡爾曼進行了抗野值的優化，但是計算量較大，過于復雜，對主控芯片有一定的要求。文獻[5]提出新的Garrote 型閾值函數，克服了軟硬閾值函數的不足，但是函數需調節的參數較多，難以掌控。文獻[6]提出將卡爾曼與小波模糊閾值進行了融合，但卻忽略了陀螺儀的低頻噪聲。針對以上問題，本文采用卡爾曼融合改進小波去噪方法，首先對原始數據進行預處理，建立MEMS 陀螺儀的時間序列模型，輸入卡爾曼濾波器進行首次濾波，然后使用改進的小波閾值去噪方法進行二次濾波，從而完成對陀螺儀信號的去噪處理。

1 基于ARMA 的卡爾曼濾波

1.1 數據預處理

為滿足時間序列模型平穩、正態、零均值的建模要求，要對陀螺儀的原始數據進行預處理[7]。采用拉伊達準則法和最小二乘法進行異常值處理與去趨勢項處理。陀螺儀原始數據預處理后如圖1 所示。

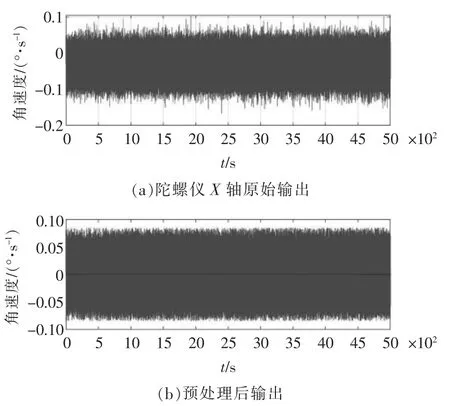
圖1 預處理前后數據對比圖Fig.1 Data comparison before and after preprocessing

1.2 平穩性及正態性檢驗

（1）平穩性檢驗

利用采用ADF（augmented dickey-fuller test）準則檢驗序列的平穩性[8]。使用Matlab 中的adftest 函數返回值為1，結果顯示該序列具有平穩性。

（2）正態性檢驗

本文采用偏態系數ξ 和峰態v 系數來檢測樣本數據的正態性，公式如下：

當ξ≈0、v≈3 時，可以認為x（t）為正態序列，求得ξ=2.8281，v=0.0018，故該序列滿足建模要求。

1.3 ARMA 模型定階和參數估計

MEMS 陀螺儀的ARMA 模型階數一般不超過3階，采用赤池信息準則（akaike information criterion，AIC）和貝葉斯信息準則（bayesian information criterion，BIC）確定具體的階數[9]。利用自回歸逼近方法求得AIC 準則與BIC 準則檢驗結果如表1 所示。通過對比發現ARMA（1，1）的AIC 和BIC 值小于其他模型，故采用ARMA（1，1），其表達式為

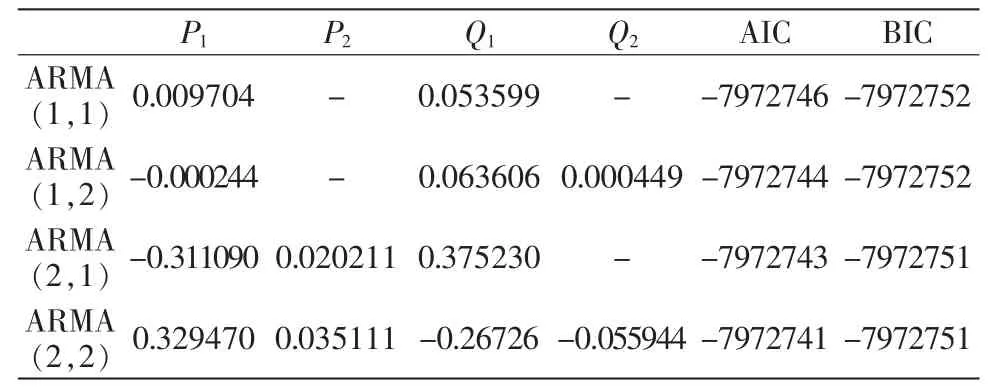
表1 AIC 準則與BIC 準則檢驗結果Tab.1 Test results of AIC criteria and BIC criteria

采用多項式擬合得陀螺儀X 軸的輸出模型：

1.4 卡爾曼濾波器設計

離散型線性隨機系統的方程為

式中：Xk為系統狀態向量；Zk為測量序列；Φk，k-1為系統轉移矩陣；Γk，k-1為輸入矩陣；Hk為觀測矩陣；Wk和Vk為系統過程噪聲序列和觀測噪聲序列，為均值為零且相互獨立的高斯白噪聲，它們的協方差矩陣分別為Qk和Rk，滿足以下特性：

式中：δkj為克羅內克爾（kronecker-δ）函數，其特性是：

則離散型卡爾曼濾波方程為

狀態一步預測方程：

狀態估計方程：

濾波增益矩陣：

預測誤差方差陣：

估計誤差方差陣：

通過以上公式可知，給定X0、P0，根據觀測值Zk即可隨時間循環更新。

2 小波閾值去噪

小波閾值去噪方法具有快速、簡單、可操作性高等優良特性[10]。基本原理：選擇合適的小波基函數對原始信號進行分解得到一系列小波系數，通過閾值和閾值函數，將高于該閾值的小波系數進行保留或適當收縮后保留，低于該閾值的小波系數歸零，最后選擇不為零的小波系數重構得到去噪后的信號。

2.1 小波閾值函數

（1）硬閾值

式中：λ 為閾值；ωj，k為去噪前小波系數；為去噪后小波系數。

（2）軟閾值

式中：sgn（）為符號函數。

硬閾值函數存在斷連、不連續等問題，導致濾波后信號出現震蕩。而軟閾值函數雖然連續，卻存在固定的偏差，會造成濾波不徹底的問題。

2.2 小波閾值

目前，常用的閾值估計方法有固定閾值、極大極小準則閾值、Stein 無偏似然閾值等。

（1）固定閾值

固定閾值λ 由Donoho 和Johnstone 提出[11]，表達式為

式中：σ 為噪聲標準差；N 為信號長度。

（2）Stein 無偏似然閾值

該方法原理是首先求得給定閾值的似然估計，然后將非似然的值進行最小化，對應的值就是所需要的閾值。

（3）極大極小準則閾值。

極大極小準則閾值是一種固定閾值，原理是產生一個最小均方誤差[11]。表達式如下：

固定閾值較為絕對，缺乏靈活性，存在“過扼殺”的問題；極大極小準則閾值過于保守，存在“過保留”的問題；無偏似然閾值對于低信噪比信號不適合[12]。

2.3 小波閾值去噪的改進方案

2.3.1 基于模糊閾值函數改進的小波閾值去噪

基于以上對常用的閾值函數和閾值的不足，本文提出通過在2 種經典閾值和模糊隸屬度函數的基礎上設計閾值函數，對小于極大極小準則閾值的小波系數進行去除，大于固定值閾值的小波系數進行保留，在極大極小準則閾值與固定閾值之間的小波系數采用模糊隸屬度函數處理。本文采用升半嶺型模糊隸屬函數對信號進行去噪[13-14]，函數表達式為

式中：ωj，k為去噪前小波系數；為去噪后小波系數；λa為極大極小準則閾值；λb為固定閾值；μA（ωj，k）為模糊隸屬度函數。

2.3.2 基于自適應小波模糊閾值去噪

由于不同頻帶的噪聲分量的不同，故本文在模糊閾值函數的基礎上引入動態調節系數r，提出了一種改進的閾值計算公式：

式中：λa為極大極小準則閾值；λb為固定閾值。

在小波分析中，信號相關度較大的小波系數相對比較大，跟噪聲相關度較小的小波系數較小[15]。故根據不同的分解尺度，每一層都選擇相應的閾值，實現分層閾值動態變化。

式中：r 為動態調節系數；j 為分解層數。

2.3.3 基于LS 改進的小波閾值去噪

對于傳統小波閾值去噪過程中只處理高頻分量部分，從而忽略了陀螺儀的低頻噪聲的不足。本文將小波分解后的低頻部分采用最小二乘對陀螺儀低頻部分進行平滑濾波，保留原有的信號趨勢。

3 實驗驗證與結果分析

3.1 仿真實驗

在仿真實驗中，利用Matlab 軟件生成原始的測試正弦信號：x（t）＝2sin（2π f1t+cos（2π f2t））；加入不同的白噪聲序列n（t）[16]，得到不同信噪比的含噪信號：y（t）=x（t）+n（t）。選取4 dB 小波經過3 尺度分解，不同的濾波方法對其進行處理，引入信噪比和均方差來反映濾波效果。對于含噪的信號，信噪比越大、均方根越小證明去噪效果越好。

如表2 所示為不同方案的信噪比與均方根，圖2 所示為信噪比為4 dB 的信號濾波結果，從實驗結果可以看出，在不同信噪比下，本文方案的信噪比均大于其他方法，均方誤差均小于其他方法。在信噪比為4 dB 下，改進的小波模糊閾值比小波模糊閾值去噪方法信噪比提高了5.143 dB，均方根減少了0.142。本文方案濾波后的信號更加還原原始信號。

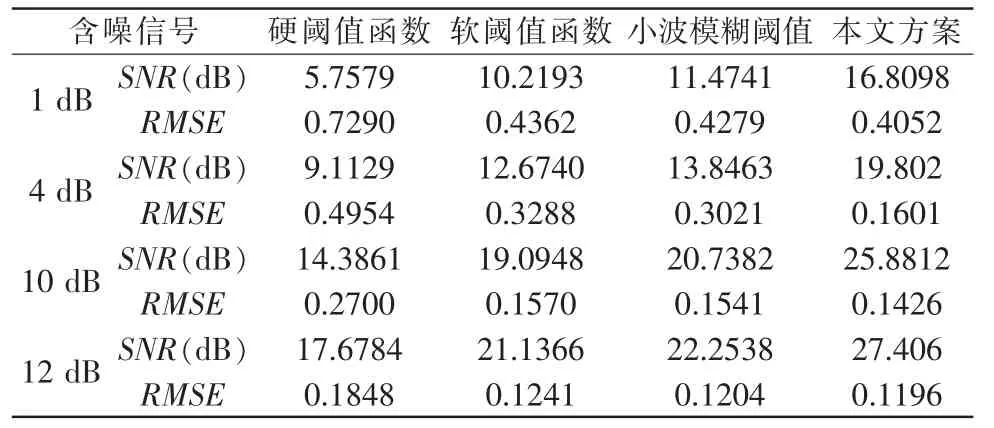
表2 不同方案的信噪比與均方根Tab.2 SNR and RMSE of different schemes

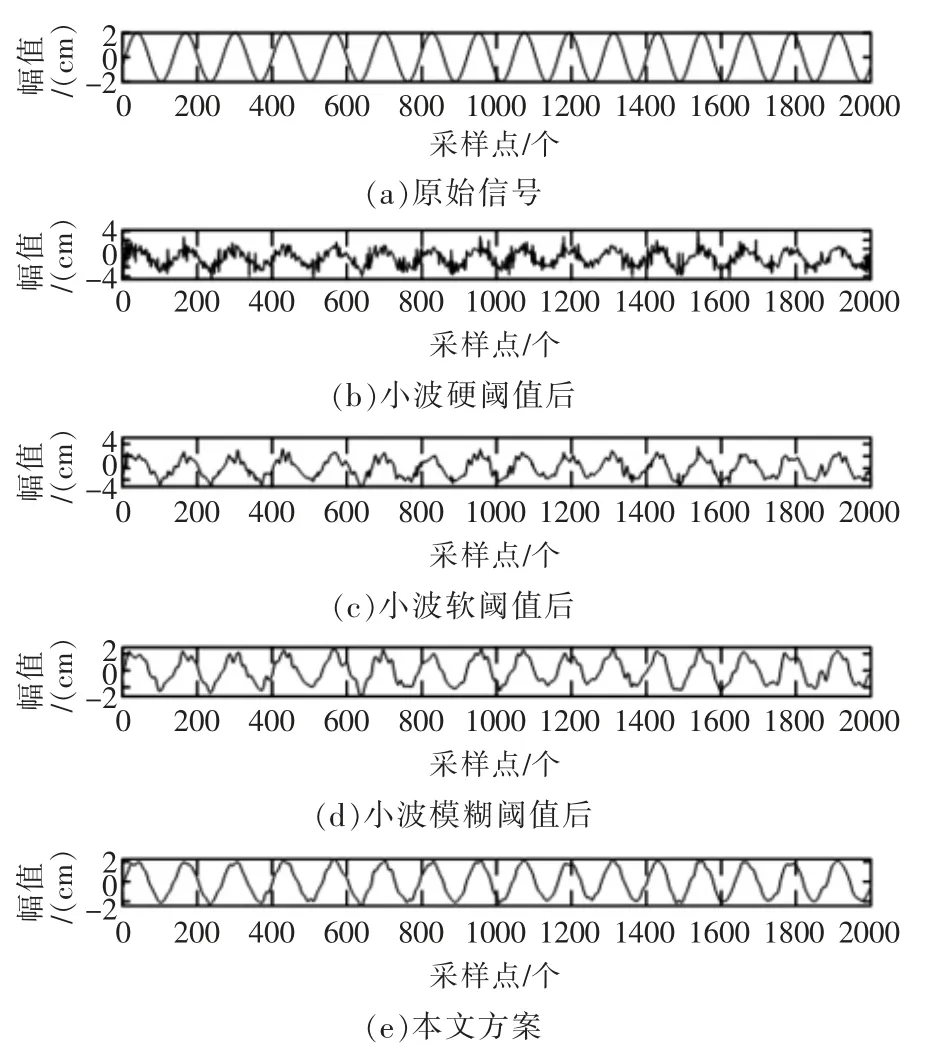
圖2 信噪比為4 dB 的信號濾波結果Fig.2 Signal filtering results with 4 dB SNR

3.2 實測數據

將MEMS 陀螺儀靜置于經緯儀控制實驗臺上保持水平，預熱30 min 后，進行數據采集，采樣頻率為200 Hz，選取連續的2000 個采樣點作為樣本數據，對其進行不同去噪方法實驗驗證。實驗采集平臺如圖3 所示。

圖3 經緯儀實驗采集設備Fig.3 Theodolite experimental acquisition equipment

不同濾波方法的前后對比圖如圖4 所示，可知本方案處理后的信號減小了毛刺，振蕩更小，更加平滑。查閱文獻可知，Allan 方差雙對數圖可以在時間頻域上根據不同噪聲在雙對數Allan 方差曲線上的斜率不同來將各個噪聲進行區分，因此常用來識別陀螺儀的隨機噪聲分量[15]。故引入Allan 方差對濾波前后MEMS 陀螺儀噪聲進行辨識，結果如表3所示。

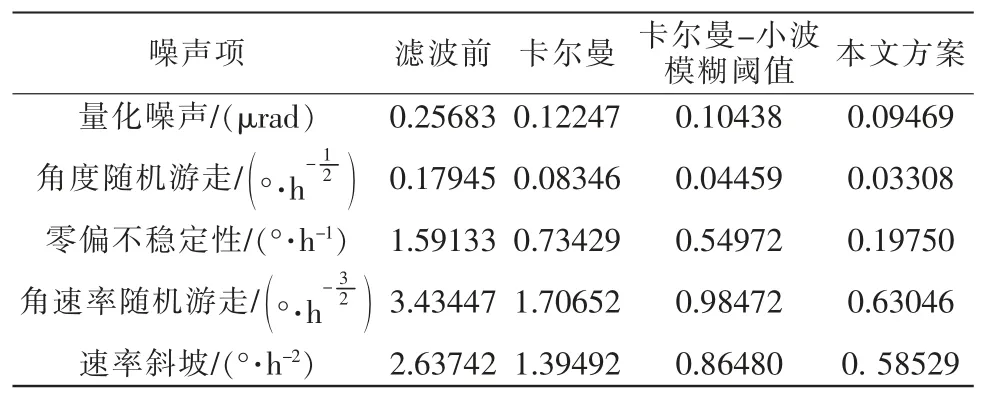
表3 Allan 方差辨識濾波前后隨機噪聲系數Tab.3 Allan variance identification random noise figure before and after filtering

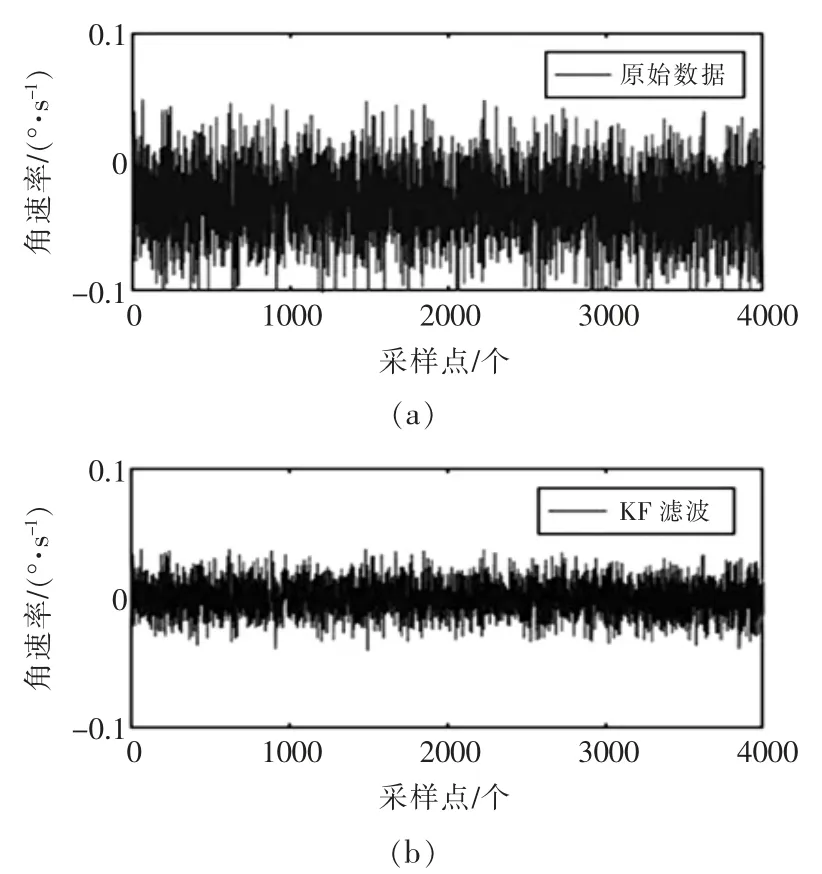
圖4 不同濾波方法的前后對比圖Fig.4 Before and after comparison of different filtering methods

實驗結果表明，利用本方案濾波后的量化噪聲、角度隨機游走、零偏不穩定性、角速率隨機游走及速率斜坡分別減少了63.17%、81.57%、87.59%、81.64%、77.80%，相比于卡爾曼濾波融合小波模糊閾值方法提高了3.82%、6.42%、22.14%、16.39%、10.59%。本文方案的濾波效果明顯減少陀螺儀的隨機噪聲，相比于傳統方法效果更佳。

4 結語

針對XGZT-XXX 型姿態傳感器輸出噪聲大、易受復雜環境干擾的問題，本文采用卡爾曼聯合改進的小波閾值方法進行去噪處理，引入Allan 方差、信噪比、均方根對陀螺儀的噪聲系數進行估計，通過仿真實驗與實測數據實驗結果表明，本文所改進的方法可以有效減小陀螺儀的噪聲，濾波效果優于卡爾曼濾波和小波閾值方法，對提高XGZT-XXX 型姿態傳感器的穩定性和抗干擾能力具有實踐意義。