基于改進離散方法的截割穩定性預測分析

謝 苗 朱 昀 劉 杰 任 澤,4 楊志勇,5 劉治翔王 賀 孟慶爽

1.遼寧工程技術大學機械工程學院,阜新,1230002.遼寧省大型工礦裝備重點實驗室,阜新,1230003.華能煤炭技術研究有限公司,北京,1000714.國家能源集團國際工程咨詢有限公司,北京,1000105.新疆露天礦智能生產與管控重點實驗室,昌吉,831100

0 引言

隨著煤礦開采技術的發展,人們對煤礦巷道斷面成形質量的要求也逐步提高。懸臂式掘進機作為智能化快速掘進的關鍵設備,對其工作的可靠性和穩定性也有了更高要求。截割機理是研究掘進機設計與制造的關鍵,一直是智能化截割的研究熱點[1-2]。侯祥明[3]對掘進機截割頭的受力進行研究,建立了掘進機整機振動方程;李曉豁[4]基于拉格朗日方程建立了整機動力學模型,提出了截割頭外載荷虛擬激勵法,研究了截割臂振動特性; 魏曉華[5]研究了掘進機擺動過程的非線性靜力學、動力學特性,分析了不同工況下掘進機截割性能; ZHANG等[6]對沖擊載荷作用下掘進機動力系統力學特性進行了研究;劉治翔等[7]研究了截割頭運動軌跡對巷道表面形貌特征的影響,得到了巷道外輪廓的創成機理;袁曉明等[8]通過仿真與實驗相結合的方法,研究了截齒截割角和旋轉角對截割載荷、載荷波動和截割比能耗的影響規律;WANG等[9]利用線性全尺度截割的原始數據,通過主成分回歸分析方法和嶺回歸分析方法,建立了鎬形齒的平均截割力和峰值截割力模型以及考慮鎬齒磨損的峰值截割力模型;XU等[10]對截割頭截齒安裝角度與截割角度的轉化關系進行研究,并通過數值仿真的方法研究了截割角度與截割阻力的關系;LIU等[11]對截齒工作角度與截割載荷的關系進行研究,獲得了截齒的工作角范圍,并通過數值模擬方法進行了截齒工作角度優化;ZHANG等[12]簡化了擺動截割中截割頭的運動,并通過數值模擬方法研究了截割深度與截割轉速對截割性能的影響,獲得了最優截割深度區間。

懸臂式掘進機的穩定工作狀態是保證它高效可靠運行的重要影響因素,而懸臂式掘進機截割過程中,由于受截割頭自身振動的影響,截割厚度會發生改變,從而誘發截割過程中動態截割力變化,引起截割顫振。截割顫振對掘進機的穩定狀態有較大影響,但近年來對截割頭截割穩定性和截割顫振的研究較少。

目前穩定性預測的方法主要有全離散法、半離散法、數值積分法等。MANN等[13-14]基于時間有限元分析(time finite element analysis,TFEA)理論分析了工件加工過程的穩定性,并對其動態加工誤差進行了同步預測;INSPERGER[15]基于半離散法進行加工過程的穩定性預測;DING等[16]提出了基于直接積分框架基礎的全離散預測方法;LI等[17-18]利用二階半離散法同時預測出顫振穩定域和動態加工誤差;LI等[19]分析了歐拉公式動力學方程的離散特性,研究了基于完全離散法的工件加工穩定性;LI等[20]對比完全離散法,提出了基于四階龍格庫塔的加工穩定性預測方法。但上述半離散方法的計算精度與計算效率偏低,全離散方法的計算精度雖有所提高,但由于狀態空間方程復雜,全離散法對解決現有問題的時間成本依舊很高。

本文在截齒破巖截割機理的基礎上,建立了單一截齒截割過程受力模型,推導了截割深度與參與截割截齒數量的關系,進而構建了單個截齒截割狀態下的力學特性方程,并基于煤礦截割和金屬切削領域的相似性,將金屬切削中的刀具顫振模型引入煤礦截割領域進行截割頭穩定性分析,提出一種基于牛頓-拉格朗日混合插值的改進全離散方法。為驗證所提出方法的有效性,搭建了截割頭-煤巖系統試驗臺,進行了截割穩定性實驗驗證,結果表明本文提出的牛頓多項式預測方法收斂速度快、預測精度高、計算耗時少,可有效提高截割頭截割可靠性,提高截割后煤巖表面平整性,能夠為高效弱顫振截割參數的選擇提供設計依據。

1 截割頭-煤巖系統動力學方程構建

1.1 截齒載荷分析

截齒在楔入煤巖時,受到截割速度前方煤巖的阻力,該力由截割動作產生,稱為截割阻力FC;截齒截割時向下擠壓煤巖,受到煤巖的反力,該力垂直于截割速度方向,由截割部的進給動作產生,稱為進給阻力FN;截齒截割成槽時,兩側煤巖脆性崩落,同時,截齒受到截槽兩側的反力,該力垂直于齒尖兩側分布,稱為側向阻力FS。處于截割狀態的截齒受力情況如圖1所示。

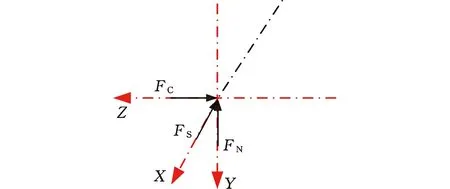
圖1 單個截齒受力Fig.1 Force on single pick

通過截割頭載荷計算經驗公式可得懸臂式掘進機在井下煤巷工作時作用在截割頭上的截割阻力[21]

FC=K1+K2h

(1)

K1=0.25pkKtKsKa+0.1pkST

和錐形截齒受到的阻力

FN=K3FC/h0.4

(2)

K3=2.5(0.15+0.000 56pk)

以及側向阻力

(3)

其中,h為瞬時截割厚度;pk為巖石接觸強度,與截割巖石硬度有關;f為巖石普氏硬度系數;Kt為截齒的類型系數,錐形齒為1.5,刀型齒為1;Ks為與截齒形狀相關的系數;Kts為刀頭形狀系數;K′ts為刀桿分布形式系數;Ktd為刀頭直徑系數;Kb為刀型齒齒間刀刃寬度影響系數,與刀刃寬度b線性相關,Kb=0.92+0.01b;Kas為刀型齒齒面前刃面形狀影響系數,平面取1,橢圓形或尖形取0.95;Ka為截齒截割角影響系數;β為平均截線間距,mm;ST為截齒后刃面磨鈍后在牽引方向的投影面積,mm2;C1、C2、C3為截齒布置系數,順序式時C1=1.4,C2=0.3,C3=0.15,交叉式時C1=1.0,C2=0.2,C3=0.1。

截割載荷主要受巖石性質參數、截齒結構和形狀以及截割頭結構以及截割頭工作參數影響,對于井下工作的懸臂式掘進機,其截齒形狀和截割頭的整體結構都基本固定,對于同一區域的煤層,煤層性質參數可視為相對固定,因此,截割載荷僅與截割厚度h與截割頭工作轉速n、截割頭鉆進速度vs有關。

1.2 截割頭載荷分析

圖2 截割頭載荷Fig.2 Cutting head load

截割頭上第i個截齒三向分力分別為

(4)

式中,φi為截齒所在的位置角,(°)。

由于截割頭整體載荷大小與參與截割的截齒數緊密相關,截割齒數又因截割頭鉆進深度、截割頭工作狀態的不同而發生改變,因此通過對截割頭形貌的實際測量能夠獲得截割深度和參與截割截齒數量的關系。假設截割頭深度為hd,截割頭參與截割的工作齒數為z,以國產EBZ160型懸臂式掘進機為例,其截割頭長度為975 mm,根據截割頭截齒位置設計參數得到截割頭截割深度與參與截割的齒數關系如表1所示。

表1 截割深度與截割齒數關系

采用最小二乘法擬合的方式對截割深度與截割頭工作齒數進行擬合,可得到在水平擺動或者垂直擺動工況下,工作區截割齒數與截割頭截割深度的函數關系式。由于截割頭齒數必須為整數,而函數擬合結果可能為小數,故對z=f(hd)向下取整:

(5)

通過最小二乘法擬合的截割深度與截割齒數關系與測量數據的對比如圖3所示,圖中柱狀圖為擬合值與測量值的誤差絕對值,從中能夠看出擬合數據與測量數據存在一定誤差,但整體偏差不大。通過R2方法對擬合效果進行評估,計算所得R2=0.995,說明整體擬合效果較好,能滿足使用要求。

圖3 截割深度與截割齒數擬合曲線Fig.3 Fitted curve of cutting depth and number of cutting teeth

同時,截割頭截割齒數還與截割頭工作狀態有關,通過下式表示:

(6)

其中,N為各工作狀態下截割區內的截割齒數,如圖4所示。

圖4 截割頭各工作狀態截割齒數Fig.4 Number of cutting teeth for each working state of cutting head

基于力線平移理論,對同一時刻位于截割區內的截齒受力進行矢量求和,得到截割頭垂直方向、水平方向、軸向方向上的三向力,其中,截割頭沿擺動方向橫切阻力為

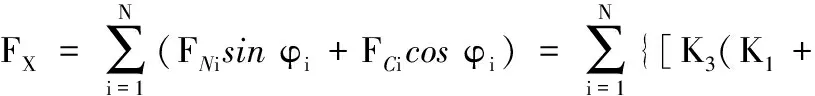
(7)

截割頭垂直方向載荷為

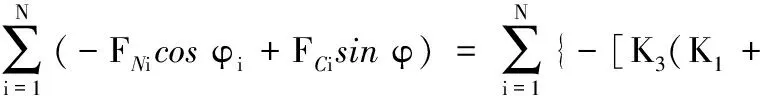
(8)

截割頭鉆進阻力為

(9)

1.3 截割頭動力學方程構建

假設懸臂式掘進機的截割頭振動幅值在彈性變形范圍內,則可根據疊加原理,將截割頭的振動視為Fx、Fy、Fz三方向軸向力單獨作用的疊加。由此,將截割頭簡化為三自由度系統,建立煤巖截割過程的截割頭系統動力學模型,如圖5所示。

圖5 截割頭系統動力學模型Fig.5 Dynamic model of cutting head system

截割頭截割運動的動力學方程表示為

(10)

F(h,t)=[F1F2F3]T

(11)

式中,M、C、K分別為截割頭的模態質量矩陣、阻尼矩陣和剛度矩陣;mx、my、mz、ζx、ζy、ζz、ωnx、ωny、ωnz分別為x、y、z方向的模態質量、阻尼比和固有頻率;s(t)為當前時刻刀具振動位移;F(h,t)為截割頭受到的截割載荷,與截割厚度與時間有關。

截齒角速度φi(t)表達式為

φi(t)=(2πn/60)t+(i-1)2π/z

(12)

判斷截齒是否參與截割的函數為

(13)

式中,ωin為第i個截齒開始截割位置;ωout為第i個截齒結束截割位置。

對于逆時針截割,ωin=0,ωout=arccos(1-ae/R);對于順時針截割,ωin=arccos(1-ae/R),ωout=π。其中,ae為徑向切深,R為截割頭半徑。

動態截割厚度hi(t)表示為

hi(t)=h0+(si(t-T)-si(t))

(14)

式中,h0為理論截割厚度;si(t)、si(t-T)分別為當前t時刻的截齒動態位移和超前一個周期對應時刻(t-T)時的截齒動態位移,如圖6所示。

圖6 動態截割厚度變化Fig.6 Dynamic cutting thickness change

由于截割厚度的變化僅體現在截割頭截割的X、Y方向,因此動態截割厚度Δh可以通過截齒動態位移表示:

Δh=-Δxsinφi(t)-Δycosφi(t)

(15)

對式(11)中含hi(t)項進行泰勒展開:

(16)

由于動態位移相對較小,可以忽略不計,故舍去展開式中高次項。

將式(14)～式(16)代入式(11)中,并將其表示成矩陣形式為

(17)

式中,αxx、αxy、αyx、αyy、αzx、αzy分別為隨時間變化的方向系數。

令

那么在結構動力學框架下,截割頭動力學方程可以表示為以下時滯微分方程:

(18)

考慮到截割力模型是線性的,故計算截割頭再生顫振穩定性時可忽略與動態位移無關的靜態量,得到

(19)

2 截割頭-煤巖系統截割穩定性預測

2.1 基于牛頓-拉格朗日混合插值方法的截割穩定性預測

令

(20)

將式(19)的動力學方程表示為狀態空間形式進行求解,得

(21)

將周期T劃分為m份(T=mτ),并利用直接積分法對狀態空間表達式進行求解,獲得式(21)的響應:

γ(t)=exp(A0(t-kτ))γ(kτ)+

(22)

當時間t=(k+1)τ時,對應的響應γk+1為

(23)

分別采用牛頓插值與拉格朗日插值對式(23)中的積分項進行近似計算,對式中A(kτ+τ-δ)與B(kτ+τ-δ)項采用一階拉格朗日方法依據(kτ,(k+1)τ)區間端點值進行插值,對式中的γ(kτ+τ-δ)項,采用三階牛頓插值多項式進行近似計算,對式中的延時項γ(kτ+τ-δ-T)采用拉格朗日多項式進行插值,通過上述插值,式(23)能夠表示為

(I-Fk1)γk+1=(F0+Fk)γk+Fkp1γk-1+
Fkp2γk-2+Fk1mγk+1-m+Fkmγk-m

(24)

(25)

因此,γk+1可以通過前一時刻的狀態響應表示,其矩陣形式為

(26)

C11=(I-Fk1)-1(F0+Fk)
Cp1=(I-Fk1)-1Fkp1
Cp2=(I-Fk1)-1Fkp2C1m=(I-Fk1)-1Fk1m
Cm=(I-Fk1)-1Fkm

截割頭狀態空間表達式對應的狀態轉移矩陣Φ可以通過映射函數Dk表示,即

(27)

依據Floquet理論,根據狀態轉移矩陣特征值的模對系統穩定性進行判定:

(28)

2.2 穩定性驗證與分析

設定截割系統X、Y、Z方向模態參數相同,截割部擺動速度vt=0.5 m/s,截割頭轉速n=45 r/min,截割的煤巖狀態為煤巖夾雜,煤巖硬度為4,巖石接觸強度pk為350 MPa[22],設置截割頭截割深度分別為200 mm、400 mm和800 mm。

對比改進混合離散法、全離散法和半離散法對本文方法進行驗證,通過局部離散誤差‖U|-|U0‖對離散方法的收斂速度進行驗證[23],其中,|U|表示狀態轉移矩陣特征值的模,|U0|為m=200時采用二階全離散方法得到的精確值。

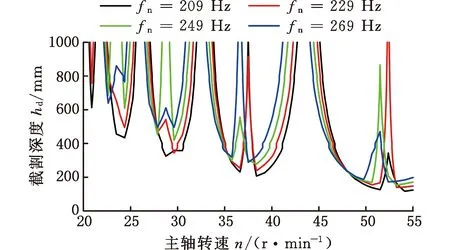
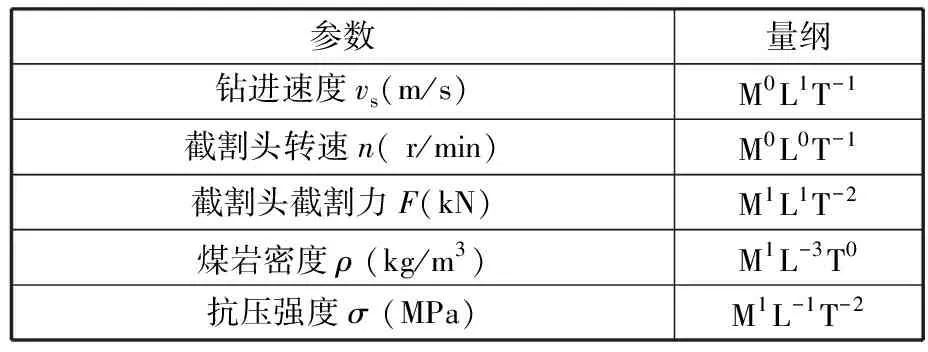
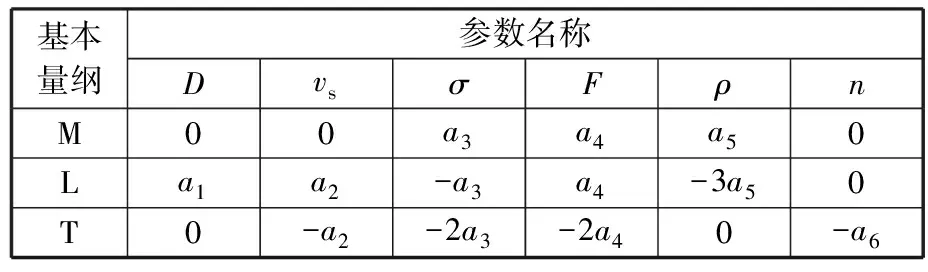
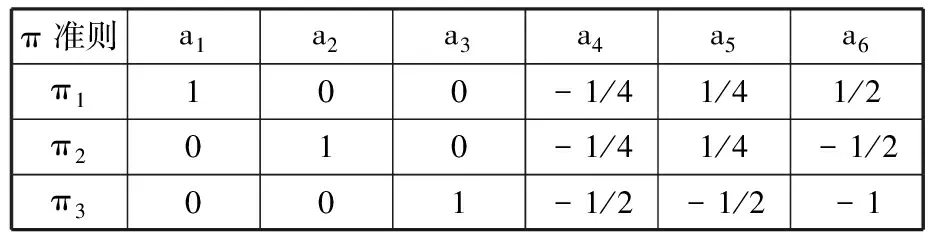
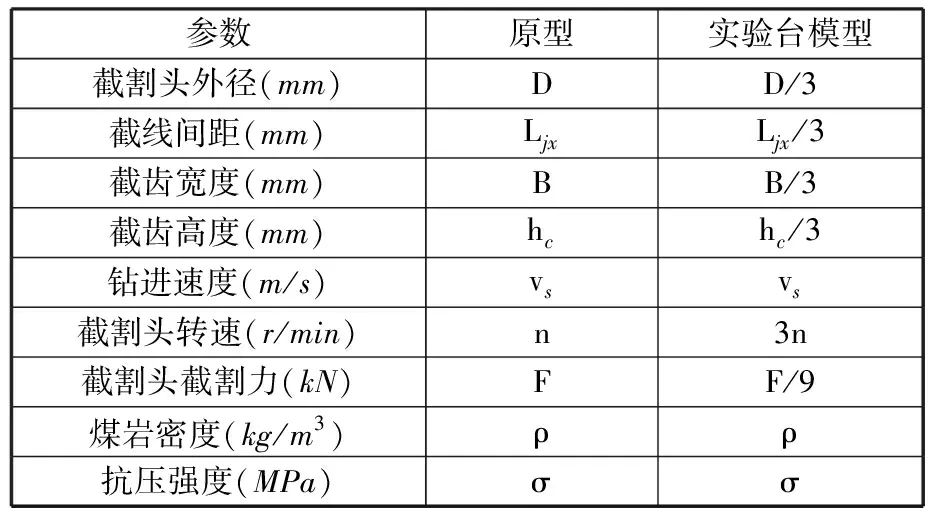
首先對改進全離散方法的收斂速度進行對比,計算得到收斂速度曲線如圖7所示。當轉速在20 r/min

(a)截割深度為200 mm收斂狀態

(a)截割深度 (b)相對誤差圖8 不同預測方法預測精度對比Fig.8 Comparison of prediction accuracy between different prediction methods

(a)截割寬度100 mm

由圖7可以看出,改進全離散方法的初始離散誤差明顯小于其他方法,隨著時間周期離散數m的增大,改進全離散方法的收斂速度也在一定程度上優于全離散法和半離散法。

為了客觀評估各方法間的收斂速度、預測精度,選用均方根誤差(root mean square error, RMSE)作為評價指標進行度量,計算公式如下:

(29)

由式(29)計算三種深度下各方法的σRMSE并取平均值,最后得到采用全離散法的均方根誤差為0.0945,半離散法的均方根誤差為0.0445,而采用改進后的離散方法計算所得的均方根誤差僅有半離散法的一半,為0.0275,這表明采用改進后的離散方法計算獲得的特征值的模在相同離散數下更加接近真實值,客觀地說明了本文方法在收斂速度上相較其他方法更快。

圖8a為不同方法計算獲得的截割深度葉瓣圖對比,而圖8b所示為不同方法獲得的截割深度預測值與準確值之間的相對誤差。由圖8可以明顯看出,隨著切割寬度的變化,每種離散方法的預測結果都有一定的偏差。但對比不同方法的相對誤差可以清楚地看到,改進的離散方法相較于其他兩種方法的相對誤差曲線處于較低的水平,表明在計算精度上具有一定的優勢。

同樣地,采用均方根誤差為評價指標對不同方法間的誤差水平進行度量,計算不同截割寬度下的均方根誤差并取平均值,最后得到的均方根誤差如表2所示。可以看出,通過改進離散方法計算獲得的截割深度均方根誤差相較于全離散方法獲得的截割深度均方根誤差減小了8.9%,表明通過改進離散方法獲得的葉瓣圖曲線更為準確,預測精度更高。

表2 不同方法均方根誤差比較

不同方法不同截割寬度下的計算時間對比如圖9所示,可以看出,隨著時間周期離散數的增大計算耗時明顯增加,而隨著截割寬度的變化,計算耗時的變化不明顯。同時對比不同計算方法間的計算時間可以得出,采用半離散與改進全離散方法的計算耗時較為接近,均較全離散方法節省約1/3的計算時間。

從上述分析中能夠看出,隨著截割寬度的變化,各離散方法預測結果均有一定偏差,預測效率也各有優劣,但在計算參數相同條件下,本文提出的改進全離散方法預測精度更高,預測效率更高、預測的穩定截割邊界更為準確。分析結果表明,相較其他離散方法,改進全離散法在幾乎不損失計算精度的情況下提高了截割頭-煤巖系統的顫振分析預測效率。

3 截割顫振影響因素分析

由上述分析建立的截割頭-煤巖系統動力學模型可知,截割系統的動力學參數對系統穩定性的預測有一定影響,過大的系統剛度與較大的系統阻尼會降低截割頭振動幅度,加載到煤巖表面會減緩系統顫振,提高系統穩定性,影響斷面成形質量。因此,本文通過改變截割系統模態剛度、固有頻率和阻尼比,研究不同的參數組合對截割-煤巖系統穩定性的影響。

3.1 系統模態剛度對顫振穩定性的影響

為了分析系統模態剛度K對系統顫振穩定性的影響,通過改變模態質量對系統模態剛度進行調整,計算得到的穩定性葉瓣圖見圖10。由圖10可知,截割深度與截割轉速間的葉瓣圖趨勢隨著剛度的增大逐步上移,截割穩定性區域面積隨剛度的增大持續擴大,系統穩定性逐步增強。

圖10 不同模態剛度下截割系統穩定性曲線Fig.10 Stability curve of cutting system with different modal stiffness

3.2 系統阻尼比對顫振穩定性的影響

對阻尼比與截割穩定性影響關系進行研究,計算得到穩定性葉瓣圖見圖11。從圖中可以看出,與系統模態剛度影響趨勢近似相同,隨著阻尼比的增大截割穩定性葉瓣圖向上移動,系統穩定性區域逐步擴大,意味著可以通過提高系統阻尼比對系統顫振穩定性進行改善。

圖11 不同阻尼比下截割系統穩定性曲線Fig.11 Stability curve of cutting system with different damping ratio

3.3 系統固有頻率對顫振穩定性的影響

為分析固有頻率對截割穩定性的影響,選用的固有頻率值為209,229,249,269 Hz,計算得到的穩定性葉瓣圖見圖12。由圖12可知,當固有頻率增大時,葉瓣圖向左移動,同時由于固有頻率對系統剛度和阻尼的影響,增大固有頻率還會使葉瓣圖逐步上移,提高相同轉速下的極限截割深度。

圖12 不同固有頻率下截割系統穩定性曲線Fig.12 Stability curve of cutting system with different natural frequencies

4 截割頭-煤巖系統穩定性實驗驗證

4.1 實驗樣機的相似準則推導

本文提出的顫振預測模型通過搭載截割頭-煤巖試驗臺進行驗證。依據相似實驗準則分別建立截割頭實驗模擬樣機、實驗模擬煤壁。

在進行截割頭實驗模擬樣機設計時,以截割頭主要參數(包括截割頭幾何參數與運動參數)與煤巖性質參數進行相似準則推導。

其中,截割頭結構參數以長度L的量綱為基本量綱,在進行相似準則推導時可以進行適當簡化,僅選取一個參數進行推導,本文選用截割頭外徑D進行參數推導,具體參數量綱表如表3所示。

表3 截割頭結構參數

而截割頭上決定截齒整體布置方法的截齒齒間夾角α、葉片沿螺旋線升角αu、截割頭上方截齒的類型及形狀、單截線上截齒數量np都是與基本量綱無關的量綱一參數,在相似準則推導時可以看成獨立π項,不參與計算。

截割頭的運動參數則包括截割頭鉆進速度vs、截割頭轉速n、截割頭截割力F。煤巖性質參數主要包括煤巖密度ρ和抗壓強度σ,具體參數量綱表如表4所示。

表4 截齒頭運動參數與煤巖性質參數及其量綱

從上述分析可知,本相似實驗模型需要考慮推導的相似準則參數共有6個,分別為截割頭外徑D、截割頭鉆進速度vs、截割頭轉速n、截割頭截割力F、煤巖密度ρ和抗壓強度σ。而由量綱分析可知,截割頭外徑D、鉆進速度vs以及抗壓強度σ能夠對應掘進機EBZ160的結構、運動以及煤巖性能參數,同時包含了三個基本量綱,因此可以選擇以上三個參數作為基本物理量參數,獲得所有6個參數的量綱矩陣,如表5所示。

表5 相似實驗樣機關鍵參數的量綱矩陣

基于上述量綱矩陣,進行相似準則推導,獲得如下方程組:

(30)

通過上述分析計算得到所選擇三個物理量相關的π矩陣如表6所示。

表6 相似實驗樣機相關參數的π矩陣

由上述推導獲得的π矩陣可以得到各相似準則參數對應的指數:

(31)

假設掘進機EBZ160的原物理量參數為x,相似實驗模型的模型物理量參數為xm,那么各參數相似系數可以表示為Cx=xm/x,根據相似第一準則,可以獲得各相關參數之間的計算表達式如下:

(32)

在建立試驗臺相似模型時,為了方便整體換算,以長度L為基準量,設其相似系數為Cl=1/Ks,Ks為設定的相似比例常數。

設定煤巖特性參數的相似性,設定煤巖密度參數的相似系數表示為Cρ=Cσ=1,由此推導出所有相似系數如下:

(33)

考慮到實驗室現有條件限制與截割實驗相似系數選取經驗[24],按照1∶3的相似比建立EBZ160掘進機的相似實驗模型,即取Ks=3,得到相似實驗臺與實際工況的參數對比如表7所示。

表7 相似實驗臺與實際工況參數對比

保證截割的幾何參數保持相對一致、實驗截割頭的轉速滿足實際掘進機截割轉速范圍(69～138 r/min),同時為了保證相似實驗模型的準確建立,將截割頭電機后置,如圖13所示。

圖13 截割頭-煤巖系統試驗臺Fig.13 Cutting head-coal rock system test bed

同樣,根據相似實驗理論建立煤壁的相似實驗模型,選用煤粉、水泥、水進行配比,取天然煤巖的抗壓強度為80 MPa[25],考慮到天然煤壁的自身裂隙與節理特征,最終確定實驗煤巖的抗壓強度為32 MPa。通過改變煤壁模型的原材料制備不同比例下的煤樣試件,如圖14所示。

(a)試件一 (b)試件二 (c)試件三 (d)試件四圖14 煤巖試件Fig.14 Test coal rock sample

最終通過濟南天辰DW-100A型電子式萬能實驗機進行單軸抗壓實驗,確定相似實驗煤壁采用的最終材料配比為1.62∶1∶0.49。

4.2 截割穩定性實驗驗證

為了驗證改進混合離散預測方法在截割顫振中的正確性,進行截割頭-煤巖系統模態參數辨識實驗,測試過程如圖13所示,截割系統測點布置如圖15所示。表8列出了力錘模態試驗獲得的截割頭模態參數。

表8 截割系統模態參數

圖15 截割系統測點布置Fig.15 Cutting system measuring point layout

為了驗證顫振穩定域曲線的正確性,進行穩定截割和顫振截割兩種工況下截割力實驗,得到截割力隨時間變化的曲線及截割頻域曲線如圖16所示。分析實驗結果可知,截割顫振發生時,截割力倍頻增大,顫振信號多集中于截割力倍頻附近,影響截割頭的穩定性。

(a)截割力時域信號

基于仿真實驗得到的截割頭模態系數及固有頻率,建立顫振穩定域曲線。為了驗證截割穩定性葉瓣圖的正確性,選用一系列截割深度與主軸轉速的組合進行實驗驗證,結果如圖17所示。可以看出,實驗結果基本符合穩定性預測狀態,表明建立的混合離散模型能夠很好地適應截割穩定性預測。

圖17 截割穩定性葉瓣圖曲線Fig.17 Cutting stability lobe diagram curve

5 結論

(1)基于懸臂式掘進機截割頭煤巖多重交互作用機理,建立了單個截齒截割載荷模型,并基于實體三維模型,擬合了截割頭截深與參與截割截齒的函數表達,基于截割頭載荷與截齒載荷的映射關系,構建了截割頭動態截割狀態力學特性方程。

(2)基于Floquet理論,選用基于牛頓-拉格朗日混合插值的改進離散方法對截割動力學方程中的動態顫振力的非齊次項進行離散求解,構建了表示截割顫振臨界穩定性的葉瓣圖曲線并與常用離散方法進行了對比驗證。結果表明,所提出的改進離散方法在收斂速率、預測精度和預測效率方面均優于全離散法和半離散法。

(3)基于改進離散方法研究了系統模態質量、剛度和阻尼比對截割系統穩定性的影響,結果表明,當其他系統參數一定時,提高系統模態剛度、阻尼比與固有頻率均能有效提高截割系統顫振穩定性,為高效弱顫振截割參數的選擇提供了一種有效方法。

(4)搭建截割頭-煤巖試驗臺進行截割頭-煤巖系統截割穩定性實驗。實驗結果表明,采用截割頭-煤巖多重交互效應與速度效應的動力學模型以及改進混合離散方法獲得的穩定性葉瓣圖能夠很好地貼近實際截割狀態,驗證了所建立的改進離散方法與動力學模型的有效性。