基于中華優(yōu)秀傳統(tǒng)數(shù)學文化的高中數(shù)學留白創(chuàng)造式教學初探

汪曉勤　鄒佳晨

【摘 要】中國傳統(tǒng)數(shù)學的歷史是中華優(yōu)秀傳統(tǒng)文化最重要的組成部分，要讓中華優(yōu)秀傳統(tǒng)文化進入數(shù)學課程和教學，教師首先需要充分利用中國傳統(tǒng)數(shù)學的歷史資源。研究者從《九章算術》中“等差數(shù)列問題”“陽馬和鱉臑問題”出發(fā)，設計留白創(chuàng)造式教學的系列任務，并提出基于中華優(yōu)秀傳統(tǒng)數(shù)學文化的若干留白策略：古名今辯，留陳述之白；古題今解，留方法之白；古術今推，留論證之白；古法今用，留發(fā)現(xiàn)之白；古問今編，留問題之白；古算今思，留超越之白。

【關鍵詞】中算史；等差數(shù)列；鱉臑；陽馬；留白創(chuàng)造式

一、引言

自2021年教育部頒布《中華優(yōu)秀傳統(tǒng)文化進中小學課程教材指南》以來，如何將中華優(yōu)秀傳統(tǒng)文化融入學科教學，成了學術界和一線教師十分關注的課題。就數(shù)學學科而言，中國傳統(tǒng)數(shù)學的歷史（以下簡稱中算史）是中華優(yōu)秀傳統(tǒng)文化的重要組成部分之一，要讓中華優(yōu)秀傳統(tǒng)文化進入數(shù)學課程和教學，教師首先需要充分利用中算史的資源。中國傳統(tǒng)數(shù)學有著悠久的歷史、輝煌的成就和豐富的內容，中算史既是數(shù)學教學的目標，也是數(shù)學教學的工具，其潛在的教育價值有待于人們去挖掘。如果僅僅將中算史視為數(shù)學教學的目標，那么教師可能僅僅會采用附加式進行教學，如介紹中國古代數(shù)學成就、數(shù)學家及其數(shù)學著作；但如果將中算史視為數(shù)學教學的工具，那么教師就需要采用更多的方式去運用有關素材，包括概念、問題、命題、法則、思想方法等，具體方式有復制式、順應式甚至重構式。

數(shù)學史告訴我們，前人留白，后人創(chuàng)新，留白是創(chuàng)新的必要條件［1-2］。類似地，在數(shù)學課堂上，教師只有留白，方能引發(fā)學生的創(chuàng)新，這正是留白創(chuàng)造式教學［3］的要義。由于古今數(shù)學表達方式、思想方法迥然不同，原原本本運用中算史料必然是遠遠不夠、甚至是沒有必要的。在留白創(chuàng)造式教學中，教師需要以中算史料為出發(fā)點設計問題，為學生提供廣闊的思維空間和足夠的探究機會，以培養(yǎng)創(chuàng)新能力，落實學科德育，從而充分發(fā)揮中算史的多元教育價值。本文以漢代數(shù)學典籍《九章算術》中的若干主題為例，從數(shù)學教學工具的角度來討論中算史在高中數(shù)學留白創(chuàng)造式教學中的應用。

二、等差數(shù)列問題

（一）《九章算術》中的等差數(shù)列問題

《九章算術》均輸章設有以下兩個等差數(shù)列問題。

問題1 今有五人分五錢，令上二人所得與下三人等。問：各得幾何？

問題1用今天的符號語言來表達就是：在等差數(shù)列a1，a2，a3，a4，a5（ai＞0，i=1，2，3，4，5）中，已知S5=5，a1+a2+a3=a4+a5，求ai。《九章算術》是從配分比例的視角來解決問題。考慮從1開始的正整數(shù)列1，2，3，4，5，該數(shù)列前3項之和為6，后2項之和為9，不滿足所求數(shù)列所要求的條件——前3項之和與后2項之和相等。在每項上加一個數(shù)p，得到數(shù)列1+p，2+p，3+p，4+p，5+p，使得（1+p）+（2+p）+（3+p）=（4+p）+（5+p），即p=[9-63-2]=3，于是得到一個滿足條件“前3項之和與后2項之和相等”的數(shù)列4，5，6，7，8。這就是說，所求數(shù)列各項之比為4∶5∶6∶7∶8，因其各項之和為5，故得各項依次為[430]×5，[530]×5，[630]×5，[730]×5，[830]×5。

三、陽馬和鱉臑問題

（一）陽馬與鱉臑

中國古代有著完備的多面體體積理論，《九章算術》給出了方亭、方錐、塹堵、陽馬、鱉臑、羨除、芻甍、芻童等多種立體圖形的體積計算方法，這些方法都是正確的。在這些立體圖形中，最基本的圖形是鱉臑。劉徽在注文中指出：“不有鱉臑，無以審陽馬之數(shù)，不有陽馬，無以知錐亭之類，功實之主也。”［4］

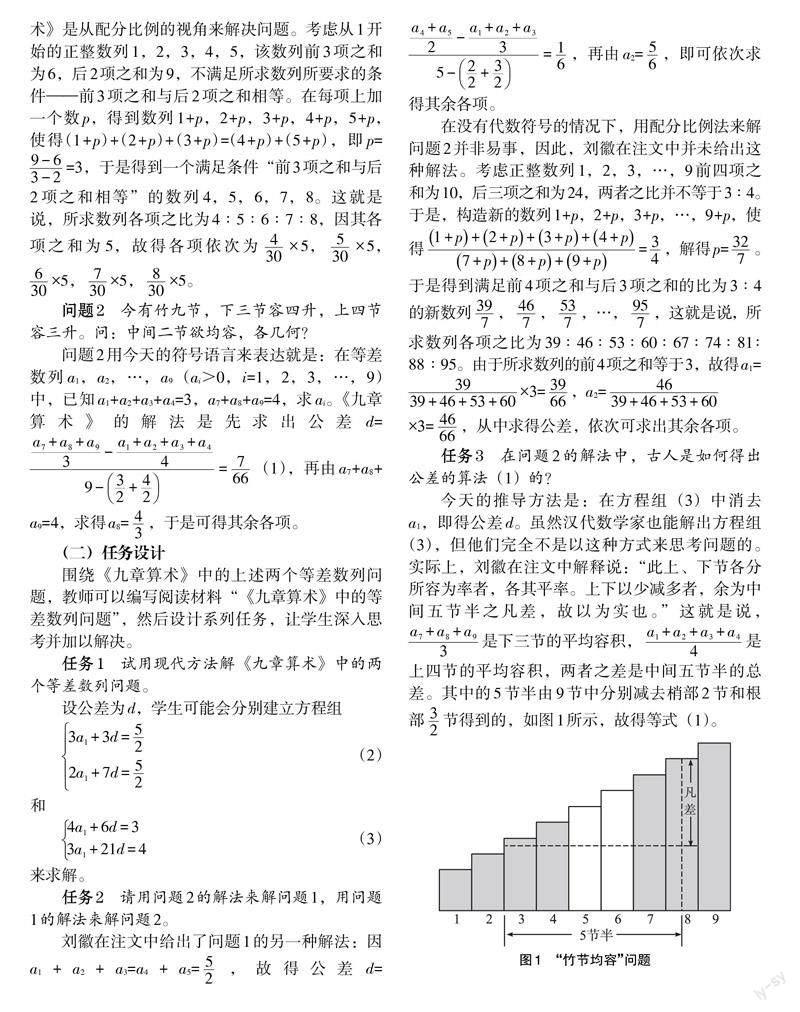
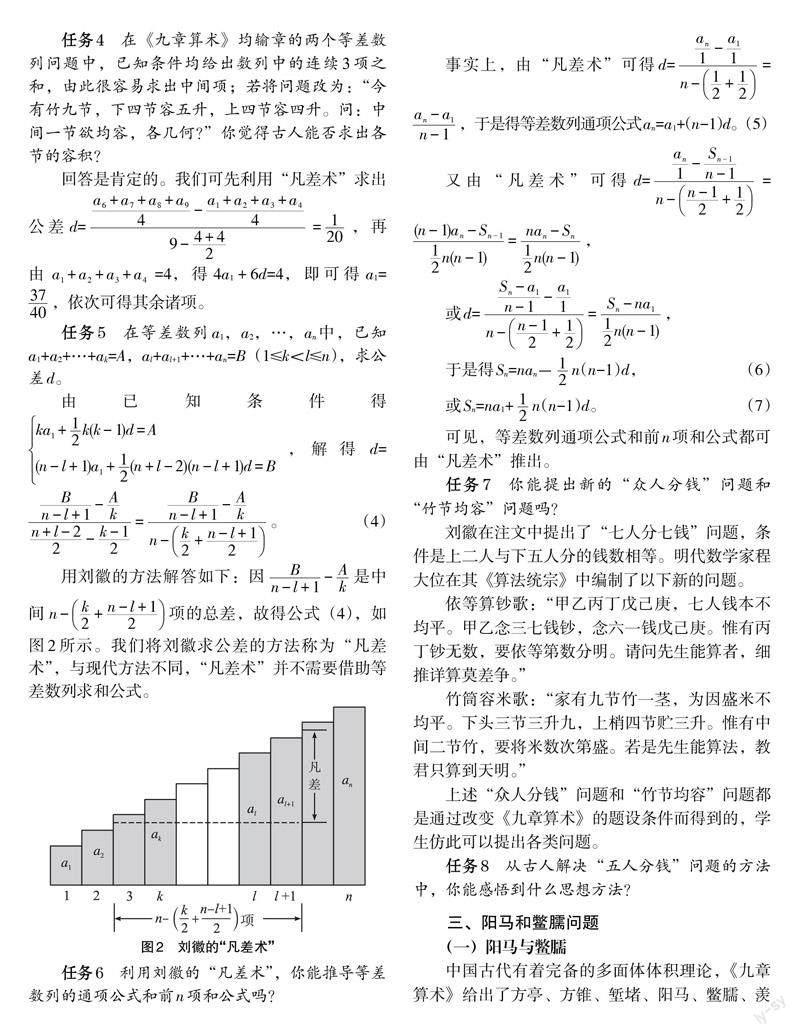
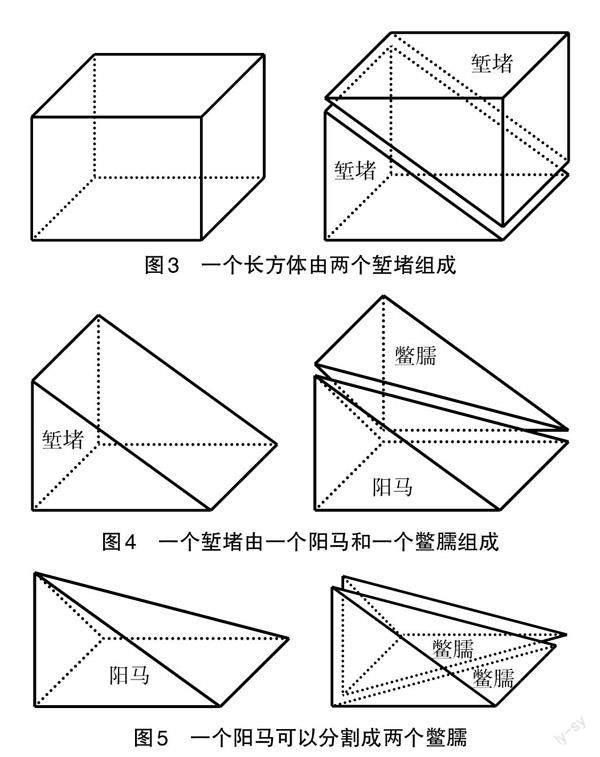
將長方體沿對角面分割，得到兩個同樣的塹堵（如圖3）；將塹堵沿對角面分割，得到一個陽馬和一個鱉臑（如圖4）；將陽馬沿過垂直于底面的棱的對角面分割，得到兩個鱉臑，古人因此也將鱉臑稱為“半陽馬”（如圖5）。

關于陽馬和鱉臑，劉徽有以下結論：（1）陽馬與鱉臑的體積之比為2∶1，今稱“劉徽原理”；（2）長方體體積是陽馬體積的3倍；（3）長方體體積是鱉臑體積的6倍。

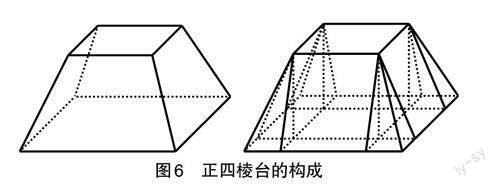
利用長方體、塹堵、陽馬和鱉臑的體積公式，可以推導方亭、方錐、羨除、芻甍、芻童等立體圖形的體積，例如：一個方亭（今稱正四棱臺）可以分割成一個長方體、四個塹堵和四個陽馬（如圖6），分別計算其體積，即可推導出正四棱臺體積公式。

（二）任務設計

圍繞陽馬和鱉臑這兩種基本立體圖形，教師可以編寫閱讀材料“中國古代立體幾何中的陽馬與鱉臑”，然后設計系列任務，讓學生深入思考并加以解決。

任務1 請給鱉臑下一個定義。

可以用以下兩種方式來定義鱉臑。

定義1：鱉臑是底面為直角三角形、有一條棱過底面非直角頂點且垂直于底面的三棱錐。

定義2：鱉臑是各面均為直角三角形的四面體。

教師還可以讓學生論證兩種定義的等價性。

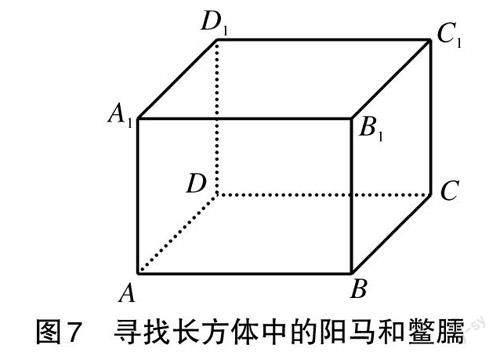
任務2 如圖7，已知長方體ABCD-A1B1C1D1，試分別將其分割成三個陽馬和六個鱉臑。

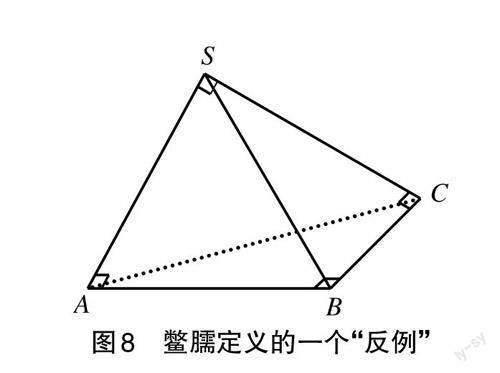
任務3 有人構造了一個反例，說明“各面均為直角三角形的四面體不一定是鱉臑”：如圖8所示，在三棱錐S-ABC的底面和各側面中，∠ABC=∠SAB=∠SCB=∠ASC=90°。請問這樣的三棱錐存在嗎？

事實上，這樣的三棱錐并不存在，因為異面直線SA和BC之間不可能同時存在兩條不同的公垂線AB和SC。

任務4 利用祖暅公理證明在同一個塹堵中，陽馬體積是鱉臑體積的2倍。

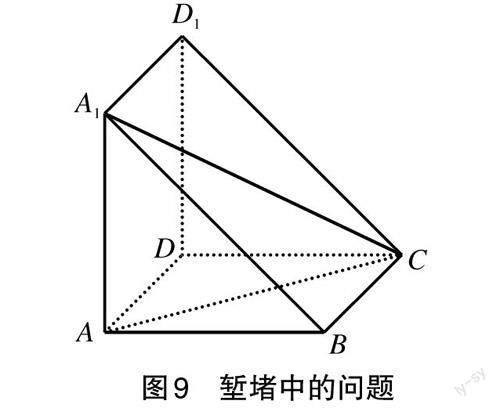
任務5 如圖9，在塹堵AA1B-DD1C中，AB=BC=AA1=1。（1）試分別求二面角A-A1B-C、A-A1C-D1、A-A1C-D和B-A1C-D的大小；（2）分別求異面直線AC和A1B、AB和A1C、A1C和AD、A1C和DD1之間的距離。

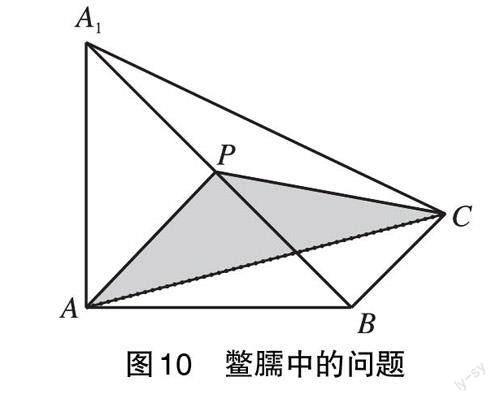
任務6 如圖10，在鱉臑A1-ABC中，P是A1B上一點，當P位于何處時，△PAC的面積最小？

任務7 利用陽馬和鱉臑，你能分別編制一個立體幾何問題嗎？

任務8 從陽馬和鱉臑問題中，你能感悟到什么思想方法？

四、基于中算史料的留白策略

在數(shù)學留白創(chuàng)造式教學中，共有6種留白形式，即陳述之白、發(fā)現(xiàn)之白、論證之白、方法之白、問題之白和超越之白［2］。從以上任務設計中可以總結出基于中算史料的若干典型的留白策略。

（一）古名今辯，留陳述之白

古名今辯指用今天的數(shù)學語言來解釋中算術語，設置古名今辯的任務，即為學生留陳述之白。中算史的許多術語都十分簡潔，如“塹堵”、“陽馬”和“鱉臑”，如果用今天的數(shù)學語言來描述，分別是“底面為直角三角形的直三棱柱”、“底面為長方形、有一條棱過底面頂點且垂直于底面的四棱錐”和“底面為直角三角形、有一條棱過底面非直角頂點且垂直于底面的三棱錐”，對于這三種特殊的立體圖形，現(xiàn)代數(shù)學中并沒有專門的名稱，因此，有必要沿用古代的術語，就像人們沿用“牟合方蓋”之名來稱謂“兩個底面直徑相等的直交圓柱體的公共部分”一樣。另一方面，中算史的術語往往源于現(xiàn)實生活，十分直觀形象，如“鱉臑”原意是“甲魚的前肢骨”，“陽馬”原意是“四柱屋隅”。教師讓學生對有關“陽馬”“鱉臑”加以定義（“陽馬和鱉臑問題”任務1），既可以培養(yǎng)他們用數(shù)學語言表達現(xiàn)實世界的能力，也可以幫助他們在具體幾何圖形中正確識別相應圖形（“陽馬和鱉臑問題”任務2），還可以增強他們應用“基本幾何體”的意識。

（二）古題今解，留方法之白

古題今解指用現(xiàn)代方法或古人的其他方法來解中算史上的某個問題，設置古題今解的任務，即為學生留方法之白。古人分別用配分比例法和“凡差術”來解“五人分錢”和“竹節(jié)均容”問題，與今人的代數(shù)解法（等差數(shù)列任務1）迥然不同，也可以互換方法，即用“凡差術”解“五人分錢”問題，用配分比例法來解“竹節(jié)均容”問題（等差數(shù)列任務2）。學生在補白過程中，對古今數(shù)學方法進行比較，既能感悟現(xiàn)代方法的優(yōu)越性，也可以建立數(shù)列和比例之間的密切聯(lián)系，還可以學會擯棄自我為中心的思維習慣，走進古人的心靈之中，從而可以站在古人的角度思考：為什么不用配分比例法來解“竹節(jié)均容”問題，為什么不用“方程術”來解“五人分錢”問題等。

（三）古術今推，留論證之白

古術今推指用現(xiàn)代方法來推導中算史上的某個公式或證明中算史上的某個命題，設置古術今推的任務，即為學生留論證之白。《九章算術》作者對于問題解決過程中涉及的公式、命題、方法的來源均不著一字，為后世留下論證之白，劉徽在注解此書時作了大量的補白工作。已知等差數(shù)列最前面若干項之和與最后面若干項之和，《九章算術》給出了公差的求法，讓學生用代數(shù)方法得出這個求法（“等差數(shù)列問題”任務3），或推測古人推導公式的方法，其實就是將中算史上的論證之白留給學生。類似地，劉徽在注文中指出，在一個塹堵中，陽馬體積是鱉臑體積的2倍，讓學生利用祖暅公理證明該結論（“陽馬和鱉臑問題”任務4），采用的是類似的留白形式。學生通過補白，既可發(fā)展邏輯推理素養(yǎng)，又可以從古人的角度來思考論證方法，實現(xiàn)跨越時空的思想交流。

（四）古法今用，留發(fā)現(xiàn)之白

古法今用指將中算史上的數(shù)學方法用于新情境、新問題，以新知創(chuàng)獲為目的，設置古法今用的任務，即為學生留發(fā)現(xiàn)之白。人們比較熟悉的例子是利用趙爽弦圖來發(fā)現(xiàn)均值不等式，類似地，利用劉徽的勾股容方圖也可以發(fā)現(xiàn)均值不等式［5］，利用出入相補原理可以發(fā)現(xiàn)兩角和與差的正弦公式［6］，等等。古法今用的留白策略，頗有點“無心插柳”的意味。劉徽僅利用“凡差術”來求等差數(shù)列的公差，并未試圖將其用于前n項和公式的推導。事實上，等差數(shù)列前n項和公式見于盈不足章“二馬相逢”問題的解法，用今日的代數(shù)符號來表達就是，南宋數(shù)學家楊輝通過構造“良馬圖”和“駑馬圖”［7］，從幾何的角度對公式加以推導。然而，與幾何方法截然不同的是，利用“凡差術”也能發(fā)現(xiàn)求和公式（“等差數(shù)列問題”任務6），在這一全新的方法中，求和公式并非建立在通項公式的基礎之上，兩者是平行的。可見，站在古人的肩膀上，今人確實能做出創(chuàng)新。

（五）古問今編，留問題之白

古問今編指從中算史上的數(shù)學問題出發(fā)編制新的數(shù)學問題。一方面，中算史料為教師留下問題之白：從中算史料出發(fā)，運用不同的問題編制策略［8］，教師可以設計豐富多彩的數(shù)學問題，如利用“條件式”策略，改變具體的條件或將條件一般化來編制問題（“等差數(shù)列問題”任務4和5）；運用“自由式”策略來編制問題（“陽馬和鱉臑問題”任務3、5和6）。另一方面，教師設置古問今編的任務，也為學生留了問題之白，如“等差數(shù)列問題”任務7和“陽馬和鱉臑問題”任務7。

除了有助于提升學生的問題提出能力，古問今編還可以讓學生跨越時空與古人對話，思考古人能否和如何解決新題，拓展古人的解法和思路。例如，在劉徽的“七人分七錢”問題中，已知前5人和后2人所得錢數(shù)相等，則由數(shù)列1，2，3，…，7構造滿足條件的新數(shù)列1+p，2+p，3+p，…，7+p時，p=-[23]，拓展了“五人分錢”問題中p取正數(shù)的情形。

（六）古算今思，留超越之白

古算今思指從中算史上有關數(shù)學問題的解法中獲取思想的啟迪，設置古算今思的任務，即為學生留超越之白。“等差數(shù)列問題”任務8與“陽馬和鱉臑問題”任務8都屬于這類留白形式。“五人分錢”問題的解法揭示了中國傳統(tǒng)數(shù)學的構造性特征：首先構造一個滿足已知條件的數(shù)列，然后用配分比例來解決問題。陽馬和鱉臑問題則揭示了中國傳統(tǒng)數(shù)學的轉化思想——化繁為簡，把多面體轉化為最基本的立體“鱉臑”和“陽馬”。此外，中國傳統(tǒng)數(shù)學問題和術語都揭示了數(shù)學與現(xiàn)實生活的密切聯(lián)系；劉徽的注解則揭示了中算家的理性精神，并有力地證明“中國古代數(shù)學沒有演繹推理和證明”這樣的觀點是完全錯誤的。

五、結語

中華優(yōu)秀傳統(tǒng)數(shù)學文化博大精深，本文所舉，不過滄海一粟；所呈現(xiàn)的任務設計，并不局限于一兩節(jié)課，也不局限于新授課或復習課。有了古名今辯、古題今解、古術今推、古法今用、古問今編和古算今思這六種策略，中算史進課程、進課堂，將不再是理想的空談，而是有法可依、易于落地的教育工程。在留白創(chuàng)造式教學中，作為教學目標的中算史，可以展示中華優(yōu)秀傳統(tǒng)文化之魅、達成數(shù)學學科德育之效；而作為教學工具的中算史，則有助于培養(yǎng)學生的核心素養(yǎng)和創(chuàng)新能力。另一方面，倘若帶著教育的眼光來研讀中算文獻，我們會深切地感受到在那些冰冷、塵封的文字背后，竟蘊藏著勃勃生機。留白創(chuàng)造式教學這一符合時代需求的教學方式，將讓中華優(yōu)秀傳統(tǒng)數(shù)學文化大放光彩。

參考文獻：

［1］汪曉勤. 數(shù)學史上的留白與創(chuàng)新［J］. 中學數(shù)學月刊，2023（4）：1-4.

［2］汪曉勤，鄒佳晨，王華. 數(shù)學史與留白創(chuàng)造式教學［J］. 數(shù)學通報，2023（3）：1-6.

［3］王華，汪曉勤. 中小學數(shù)學“留白創(chuàng)造式”教學： 理論、實踐與案例［M］. 上海：華東師范大學出版社，2023.

［4］郭書春. 匯校九章算術［M］. 沈陽：遼寧教育出版社，2004.

［5］汪曉勤. 從“勾股容方”到均值不等式［J］. 數(shù)學通報，2015（2）：7-9.

［6］汪曉勤，邵銘宇. 三角公式的若干幾何模型［J］. 數(shù)學通報，2017（6）：1-5，49.

［7］汪曉勤，陳君煜. HPM視角下數(shù)列教學中的直觀想象素養(yǎng)初探［J］. 中小學數(shù)學（高中版），2019（4）：57-60.

［8］汪曉勤. 基于數(shù)學史料的高中數(shù)學問題編制策略［J］.數(shù)學通報，2020（5）：9-15.

（責任編輯：陸順演）

【作者簡介】汪曉勤，華東師范大學教師教育學院教授，博士生導師，主要從事數(shù)學史與數(shù)學教育、數(shù)學教師教育研究；鄒佳晨，博士，華東師范大學教師教育學院講師，主要從事數(shù)學史與數(shù)學教育、數(shù)學教師教育研究。

【基金項目】上海高校立德樹人人文社會科學重點研究基地之數(shù)學教育教學研究基地研究項目“中華優(yōu)秀傳統(tǒng)文化進數(shù)學課堂的實踐研究”；上海市第四期雙名工程課題“中小學數(shù)學留白創(chuàng)造式教學”