基于MATLAB平臺的懸臂梁靜力彈性分析

譚 宸

(同濟大學土木工程學院,上海 200092)

0 引言

有限單元法是當今工程分析中獲得廣泛應用的數值方法[1],采用有限元方法可以求解具有復雜的幾何邊界的彈性問題。曹子龍等[2]建立了求解圓孔薄板彈性問題的雜交應力單元,推導出圓孔薄板問題的極坐標下應力插值矩陣,可較高精度的求解孔邊附近應力。陳立勝等[3]采用有限單元法初步對彈性平面問題進行了初步嘗試。張明哲等[4]開發的計算軟件平臺有助于學生很好的理解在彈塑性問題中改進無單元Galerkin方法的應用。目前,伴隨著有限元軟件功能的不斷完善,對于剛接觸有限元軟件的學生而言,往往對其一知半解,在有限元分析中著重于物理參數的調節[5]。

為了加深學生們對于有限元方法基本原理的理解,本文通過基于MATLAB平臺,編寫結構化的有限元代碼,可以應用于基本的結構工程問題。該代碼的結構易于理解,并可由學生輕松擴展。本文開發的代碼計算懸臂梁變形結果與商業有限元軟件ABAQUS計算結果一致,開發的一個結構良好、易于使用的計算懸臂梁結構彈性變形的有限單元分析程序具有很好的適用性。

1 彈性問題的有限單元格式

工程中許多問題,通常是以未知場函數在域內應滿足的偏微分方程形式提出。根據彈性力學基本方程和與之等效的變分原理,可以從基本方程的強形式推導出有限元格式,進而可獲得局部單元剛度矩陣。

本小節以二維平面域中彈性問題為例,考慮邊界條件,對其偏微分方程的有限元格式進行推導。從面積域中取一無限小單元,其受力示意圖如圖1所示。

從圖1可以看出,該單元的平衡方程可表示為:

(1)

(2)

用笛卡爾張量符號可以進一步將彈性力學平衡方程改寫為:

σji,j+bi=0 (i,j=1,2)

(3)

通過加權余量法可寫出平衡微分方程的等效積分弱形式。等效積分弱形式可以通過分部積分得到:

(4)

作為平衡微分方程的等效積分弱形式,在導出過程中并未涉及物理方程,因此,不僅僅可以適用于線彈性問題,還可以用于非線性彈性或者彈塑性問題。

將權函數wi替換成δui,可以得到有限單元法的控制方程:

(5)

改寫成矩陣形式可得:

(6)

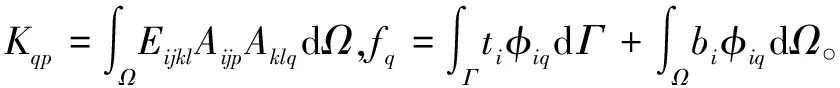
本文采用4結點矩形單元來處理二維平面彈性力學問題,4結點矩形單元如圖2所示。

對于每個角點,構造出它的形函數為:

(7)

進一步,根據彈性力學中位移與應變的關系,可將單元應變用結點位移向量來進行表示:

{ε}=εxεyγxyì?í????üty????=N1(x,y)x0N2(x,y)x0N3(x,y)x0N4(x,y)x00N1(x,y)y0N2(x,y)y0N3(x,y)y0N4(x,y)yN1(x,y)yN1(x,y)xN2(x,y)yN2(x,y)xN3(x,y)yN3(x,y)xN4(x,y)yN4(x,y)xé?êêêêêêêù?úúúúúúúüty??????????????????????????????????[B] u1 v1 u2 v2 u3 v3 u4 v4u1v1u2v2u3v3u4v4ì?í???????????üty???????????(8)

將形函數代入可得梯度矩陣[B]:

(9)

局部單元剛度矩陣K:

(10)

代入B矩陣,進而可以得到:

[K]= u1 v1 u2 v2 u3 v3 u4 v4k11k12k13k14k15k16k17k18k21k22k23k24k25k26k27k28k31k32k33k34k35k36k37k38k41k42k43k44k45k46k47k48k51k52k53k54k55k56k57k58k61k62k63k64k65k66k67k68k71k72k73k74k75k76k77k78k81k82k83k84k85k86k87k88é?êêêêêêêêêêêù?úúúúúúúúúúúu1v1u2v2u3v3u4v4(11)

其中,

。

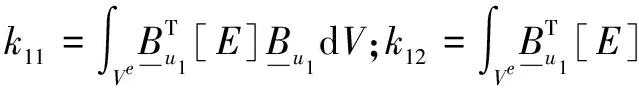
2 程序架構

該程序基于MATLAB編程語言開發,依托于有限單元法解決彈性問題,可以高效便捷的對懸臂梁受集中荷載作用下的應力應變進行分析。程序通過先對幾何域進行單元網格劃分,建立節點和對單元進行編號,隨后輸入邊界條件等模型數據,對其進行采用有限單元法的彈性分析后得到處理結果,最后將結果云圖以可視化的界面進行展示。程序可以分為前處理程序、有限元彈性分析計算程序和可視化后處理程序三個部分,其流程圖和MATLAB函數如圖3所示。

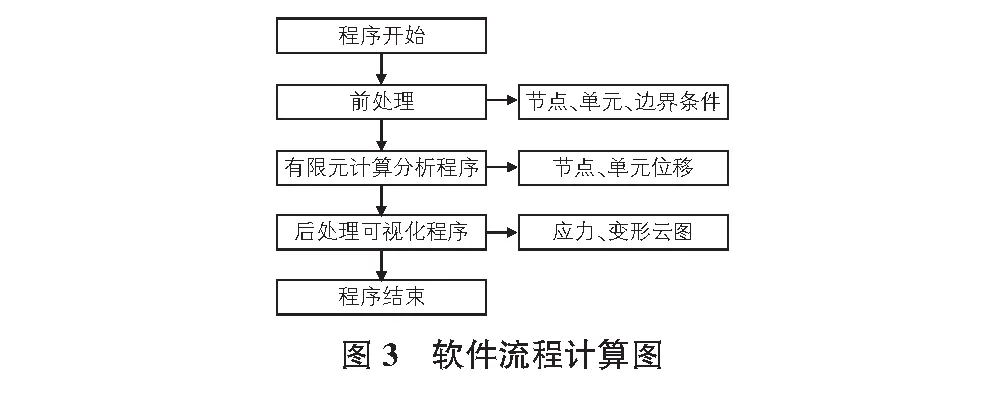
前處理程序主要是通過建立幾何模型,生成節點和網格,將分析域離散化,組建全局坐標系統,同時引入邊界條件。輸入參數后預處理必備的結構參數值,前處理關鍵環節需要定義節點、生成每個單元坐標信息、輸入載荷信息和邊界條件,為有限元法分析做準備。計算分析程序進行有限單元法的計算,最主要的是進行矩陣計算和求解。計算分析程序通過求解全局剛度矩陣獲得每個節點的位移{u},進而評估每個單元上的應力和應變。后處理程序模塊對每個單元建立節點位移和應力向量,進而繪制加載后模型的位移、應力云圖,實現計算結果的可視化。

2.1 前處理程序

前處理程序是數值計算中非常重要的環節,影響后續數值計算的精度和效率。前處理可分為如下部分:輸入材料形狀大小、材料性質參數、生成節點坐標等單元信息以及載荷和邊界條件定義等。

前處理程序的首要是生成節點坐標,包括節點的編號及相應的點的坐標值。節點位置信息定義為函數square_node_array,生成節點信息后,需要獲取每個單元的節點信息。節點的空間信息存儲在element數組中。為便于后續邊界條件的處理,方便使用,按照單元中節點逆時針編號進行存儲記錄,在完成節點的計算、單元節點信息的輸入后,編寫supportcond函數引入邊界條件。對于懸臂梁在端部受集中荷載而言,其荷載位移邊界條件的matlab代碼如下:

function [topEdge,topEdge1,dispNodes,dispNodes1,leftNodes1]=supportcond(numx,numy)

nnx=numx+1;

nny=numy+1;

uln=nnx*(nny-1)+1;

urn=nnx*nny;

lrn=nnx;

lln=1;

topEdge=[uln:1:(urn-1);(uln+1):1:urn]′;

topEdge1=topEdge;

botEdge=[lln:1:(lrn-1);(lln+1):1:lrn]′;

rightEdge=(lrn:nnx:(urn))′;

botNodes=unique(botEdge);

topNodes=unique(topEdge);

rightNodes=unique(rightEdge);

leftNodes=rightNodes-(nnx-1);

dispNodes=botNodes;

rightNodes1=rightNodes(2:end);

leftNodes1=leftNodes(2:end);

dispNodes1=leftNodes;

end

2.2 有限元計算分析程序

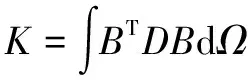
其中,B矩陣的matlab代碼如下:

function Bfem=Bmatrix(pt,iel)

global node element

sctr=element(iel,:);

nn=length(sctr);

[N,dNdxi]=shape_func(pt);

J0=node(sctr,:)′*dNdxi;

invJ0=inv(J0);

dNdx=dNdxi*invJ0;

Bfem=zeros(3,2*nn);

Bfem(1,1:2:2*nn)=dNdx(:,1)′;

Bfem(2,2:2:2*nn)=dNdx(:,2)′;

Bfem(3,1:2:2*nn)=dNdx(:,2)′;

Bfem(3,2:2:2*nn)=dNdx(:,1)′;

end

2.3 后處理可視化程序

后處理程序獲取有限元計算分析程序得到的位移等信息,并重新組織成標準后處理結果文件的形式,利用matlab可視化技術再現網格信息,將變形前后的網格展示出來。同時,分析計算結果,如位移云圖、應力云圖的結果以圖像形式顯示出來。本系統的后處理程序包括數據處理程序、圖像顯示程序。

3 數值算例計算與驗證

3.1 算例計算

對二維受集中力的懸臂梁采用彈性問題的有限單元法進行小變形數值分析。通過對該懸臂梁進行自主編程建模,建模核心代碼流程如第2小節所示。利用前處理程序模塊在梁內布置節點,進行單元編號,記錄每個單元的節點信息。將輸入節點信息和荷載位移邊界條件輸入到有限元分析計算程序中,進而計算獲得節點的位移和應力、應變等數據。將所得結果與ABAQUS軟件分析結果進行比較,驗證了本文提出的彈性問題有限單元法程序的有效性,可進一步加深學生們采用有限元法分析問題編制程序的理解。

懸臂梁自由端受集中荷載示意圖如圖4所示。梁的幾何尺寸為L=10 m,D=1 m,梁的厚度為t=0.1 m。梁受集中荷載P=0.1 N。材料的彈性模量為E=100 kPa,泊松比為v=0.25,按照平面應力問題進行求解。

采用前處理程序進行結點生成,單元網格劃分,水平劃分單元數為100,豎向劃分單元數為10,結果如圖5所示。

將節點信息和荷載條件輸入到有限元分析計算程序中進行計算,獲得變形后的懸臂梁有限單元網格如圖6所示。

懸臂梁的位移云圖如圖7所示。

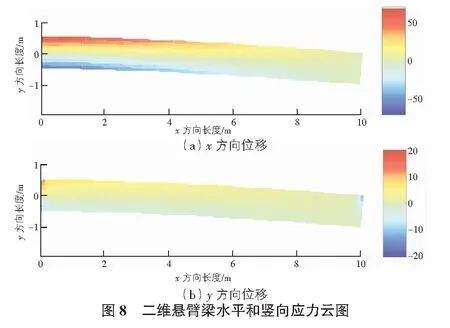
從圖7中可以看出,右端部頂處豎向結點位移為0.039 8 m。水平應力σxx與豎向應力σyy云圖見圖8。

3.2 方法驗證

基于ABAQUS有限元的數值模擬方法是檢驗本文程序編制的正確性的有效途徑之一。本小節通過建立與3.1算例相同的懸臂梁結構有限元模型,并對模型賦予材料參數、施加集中荷載邊界條件,驗證本文方法的正確性。

在ABAQUS中,建立的懸臂梁三維結構幾何參數為L=10 m,D=1 m,t=0.1 m。懸臂梁材料彈性模量E=100 kPa,泊松比為v=0.25。有限元模型如圖9所示。在有限元模型中,所施加的載荷為力載荷。模型網格劃分如圖10所示。

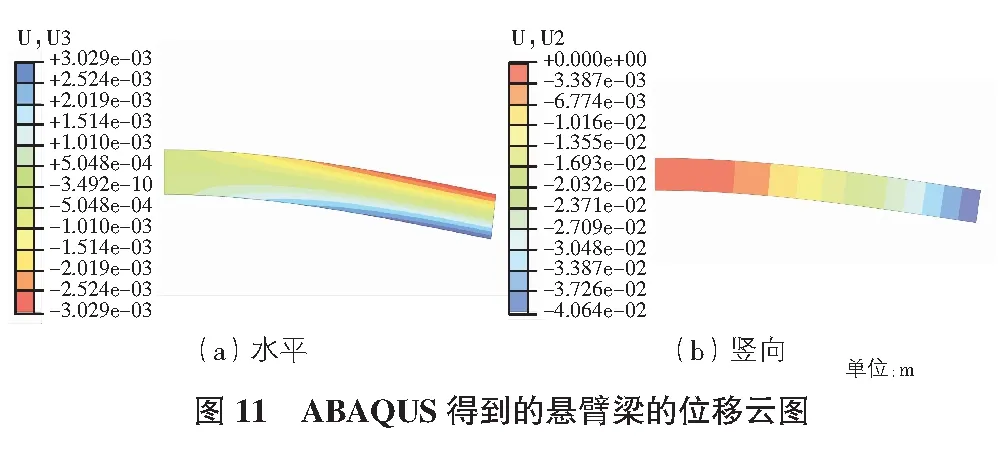
ABAQUS計算獲得的懸臂梁的位移云圖如圖11所示,從圖11中可以看出,右端部頂處豎向結點位移為0.040 m。水平應力σxx與豎向應力σyy云圖見圖12。

通過將本文編寫的懸臂梁有限單元法程序與ABAQUS計算的結果進行對比,可以看出,所開發的基于MATLAB平臺的懸臂梁彈性分析程序可以較好的預測梁的小變形,所得計算結果與有限元軟件計算結果一致。

4 結論

本文以求解懸臂梁受集中荷載作用下變形為算例,介紹了有限單元法求解彈性問題的算法。通過將商業有限元分析軟件結果與本文程序編制結果對比,兩者一致,驗證了本文程序的有效性。該程序基于MATLAB平臺編制而成,程序簡單實用,計算效率比采用有限元軟件ABAQUS分析彈性問題的效率更高。本文展示的有限元求解彈性問題的方法通用性強,通過該程序,可以進一步加深學生們采用有限元法分析問題編制程序的理解,具有重要意義和參考價值。通過對該程序的學習,可以舉一反三,在該程序的基礎上修改荷載和位移邊界條件,進一步求解其他的彈性問題。