基于逐步—主成分回歸的設施番茄果期生長模型研究*

王淵龍，張艷，柳平增

(1. 山東農業大學信息科學與工程學院,山東泰安,271018; 2. 山東農業大學農業大數據研究中心,山東泰安,271018; 3. 農業農村部黃淮海智慧農業技術重點實驗室,山東泰安,271018)

0 引言

設施農業是由傳統農業向現代化集約型農業轉變的有效方式,是實現農業現代化的必由之路,在國內外農業結構調整中發揮重要作用[1-2]。其中番茄是我國設施蔬菜主栽品種之一,具有易于栽培、市場需求量大、經濟效益高等特點,栽培面積和產量均居我國設施農業首位[3]。設施番茄具有較高的科研和經濟價值,以設施番茄為研究對象具有重要的意義[4]。在國內外關于番茄生長模型的研究中,大多數學者以光溫或光溫濕為主要因素構建了番茄生長模型,如張智優等[5]對不同播期、品種、氮素水平及茬口的試驗數據進行處理,構建了反映果實生長與溫度、光照關系的果實橫、縱徑生長模型,以及果實干物質機理性模型和果實鮮重與橫、縱徑關系的線性模型,并建立了以上述模型為基礎的番茄產量預測模型;程智慧等[6]將空氣溫濕度和光照強度細分為7個變量,運用逐步回歸建立了顯著環境因子與果實日增量的回歸模型;Uzun[7]通過分析溫度和光照強度,建立了番茄葉片數生長發育模型;Gupta等[8]研究了設施條件下累積輻熱積對番茄幼苗長勢的影響。部分學者在光溫濕基礎上以空氣CO2濃度、水分、營養元素等為主要因素構建了番茄生長模型,如劉新英等[9]以CO2濃度和營養液含氮量為自變量,利用多元線性回歸方法建立了番茄全周期的光合速率預測模型;雷濤等[10]為探究不同水分—沸石量—埋深條件下番茄的生長特性,采用Logistic模型模擬了番茄生長動態過程,揭示了各因素對番茄物候期和生長參數的影響;李佳佳等[11]為研究高溫脅迫下設施番茄植株氮素運營規律,開展了高溫和施氮量雙因素全面試驗,發現設施番茄臨界氮濃度與地上部干重之間符合冪指函數關系;荷蘭的Spitters等[12]建立了TOMSIM番茄生長模型,綜合考慮了番茄植株不同冠層的光照、葉面積指數、其他生理作用及溫室環境等要素。

綜上所述,國內外學者在研究環境要素對番茄生長發育的影響上,多以溫光為主;在分析方法上,多以相關性分析、多元線性回歸為主。但溫室環境要素較復雜,還需考慮變量間是否存在多重共線性,否則會難以區分每個解釋變量的單獨影響,變量的顯著性檢驗失去意義,回歸模型也會缺乏穩定性[11]。設施番茄果實生長是影響產量形成的一個重要指標[13],本文擬用設施番茄果期生長數據和環境數據,分析數據間的相關性和多重共線性,然后采用逐步回歸和主成分回歸組合方法構建設施番茄果期生長模型。

1 材料與方法

1.1 試驗區概況

試驗于2020年8月—2021年2月在山東省德州市陵城區糜鎮智慧農業產業園進行。溫室呈東西走向,長125 m,寬10 m,北側墻體厚7.5 m。試驗供試番茄品種為“凱德87170”,此品種為大紅果,無限生長型。溫室采用龔作種植模式,龔寬0.65 m,溝寬0.55 m,壟內雙列栽種,分別于8月6日、8月31日和9月24日在番茄幼苗5葉1心時按株距30 cm、行距35 cm各定植1 200顆,共種植3 600顆。試驗統一水肥及其他農事操作。

1.2 指標測定

設施番茄果期生長模型由設施番茄生長數據和溫室內環境數據構建,它們分別由物聯網設備、信息化設備及人工方式采集。

設施番茄生長數據由信息化設備和人工每7天采集一次,采集時選取10株長勢一致的樣本并采集樣本株高、莖粗、葉片數、葉面積、果實橫縱徑等指標,共采集210條生長數據,其中葉面積使用國產LA-S植物圖像分析儀計算測得,莖粗由作物莖粗測量儀測得,株高采用卷尺測得。

溫室內環境數據由山東農業大學大數據研究中心自主研發的“神農物聯”設備每隔30 min自動采集一次,共采集4 704條環境數據,采集指標包括空氣溫度、空氣濕度、二氧化碳濃度、光照強度、土壤溫度等,使用傳感器型號如表1所示。

表1 傳感器型號Tab. 1 Sensor type

1.3 數據預處理

溫室內環境數據由物聯網設備每隔30 min采集一次,用程序處理后得到各環境變量日平均值及累計值;設施番茄生長數據由人工和信息化設備每隔7天采集一次,用程序處理后得到各生長指標的平均值。將處理后數據進行標準化得到試驗最終數據。本研究使用前兩批數據進行分析,第三批數據進行驗證。

1.4 相關方法

1) 逐步回歸。逐步回歸分析方法的基本思路是自動從大量可供選擇的變量中選取最重要的變量,建立回歸分析的預測或解釋模型。其基本思想是:將自變量逐個引入,引入的條件是其偏回歸平方和經檢驗后是顯著的。同時,每引入一個新的自變量后,要對舊的自變量逐個檢驗,剔除偏回歸平方和不顯著的自變量。一直這樣邊引入邊剔除,直到既無新變量引入也無舊變量刪除為止。它的實質是建立“最優”的多元線性回歸方程。

依據上述思想,可利用逐步回歸篩選并剔除引起多重共線性的變量,其具體步驟如下:先用被解釋變量對每一個所考慮的解釋變量做簡單回歸,然后以對被解釋變量貢獻最大的解釋變量所對應的回歸方程為基礎,再逐步引入其余解釋變量。經過逐步回歸,使得最后保留在模型中的解釋變量既是重要的,又沒有嚴重多重共線性。

2) 主成分回歸。主成分回歸通過以主成分為自變量解決多重共線性,它先用主成分分析消除回歸模型的多重共線性,然后將主成分作為自變量進行回歸分析,最后根據得分系數矩陣將原變量代回得到新模型。

主成分分析是考察多個變量間相關性的一種多元統計方法,它把多個變量化為少數幾個互相無關的綜合變量,并使綜合變量盡可能地代表原來信息,具有明顯的降維優勢。用主成分提取的新變量組內差異小而組間差異大,可以有效地消除多重共線性問題。

2 基于逐步—主成分回歸的設施番茄果期生長模型的構建

番茄的果實生長是影響產量形成的重要指標,果實橫徑能在一定程度上反映番茄在果期的生長變化情況[14],因此以果實橫徑為因變量,以溫室內空氣溫度、光照強度、空氣濕度、二氧化碳濃度以及土壤溫度累計量為自變量構建設施番茄果期生長模型。用Y表示果實橫徑,用X1～X5分別表示果期溫室內各環境因子。

2.1 設施番茄果期數據相關性分析

數據分析前應先對數據從整體上有所認識。散點圖陣表示各變量隨其他變量變化的大致趨勢,能夠反映多個變量間的相關關系,據此選擇合適的函數對數據點進行擬合。

用果實橫徑同各環境因子繪制散點圖陣,觀察數據間的相關關系。圖1為果實橫徑與各環境因子的散點圖陣。

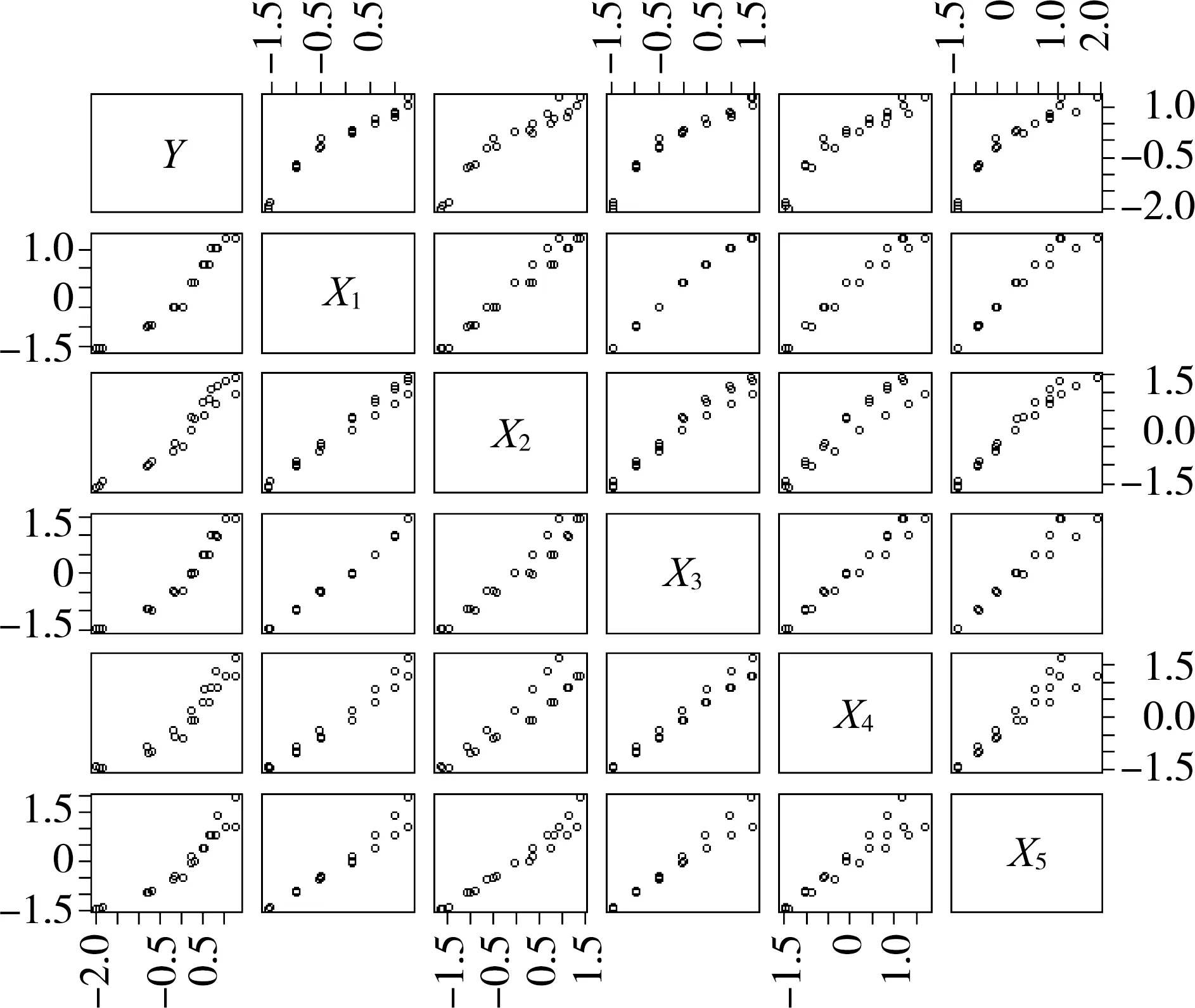
圖1 果實橫徑與各環境因子散點圖陣Fig. 1 Scatter plot of fruit horizontal stems and environmental factors

由圖1可知,果實橫徑與各環境因子間均存在明顯的線性相關關系。

散點圖陣可以直觀地展示數據間的關系,判斷數據間的變化趨勢,但只能用來大致觀測數據的特點。在統計學中,皮爾遜相關系數,又稱皮爾遜積矩相關系數,是用于度量兩個變量X和Y之間的線性相關,其值介于-1～1之間[15],它可以用數值精確地說明數據間的相關關系,使用散點圖陣初步分析數據特點,再利用皮爾遜相關系數能進一步探明數據間的線性相關程度。使用皮爾遜相關系數的前提條件是數據服從正態分布[16],因此在使用皮爾遜相關系數之前應先用正態分布檢驗方法判斷數據是否服從正態分布。

在顯著性水平為0.05的情況下所有變量的p值均通過檢驗,且所有變量的w值接近于1,故各變量均服從正態分布,符合使用皮爾遜相關系數的前提條件,因此可以使用皮爾遜相關系數來查看數據間的相關程度。表2為果實橫徑與各環境因子的相關系數表。

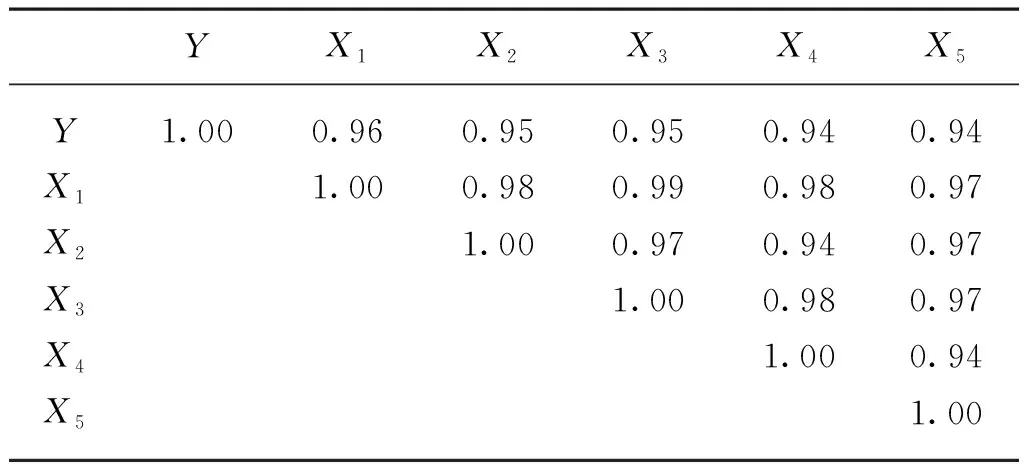
表2 相關系數表Tab. 2 Correlation coefficient

由表2可知,果實橫徑與各環境因子間的相關系數分別為0.96、0.95、0.95、0.94、0.94,說明果實橫徑與各環境因子間存在較強的相關關系,此外各環境因子間也存在較強的相關關系,故將五個環境因子全部引入用來構建模型。

2.2 設施番茄果期數據多重共線性分析

由皮爾遜相關系數分析結果發現果實橫徑與各環境因子間存在較強的相關關系,因此每個環境因子都不能被忽略。多元線性回歸是構建模型最常見的方法,因此首先使用多元線性回歸建立果實橫徑與各環境變量間的關系模型,量化分析果實橫徑與各環境因子間的關系,同時觀察多元線性回歸對于設施番茄果期數據是否有效。多元線性回歸結果如表3所示。

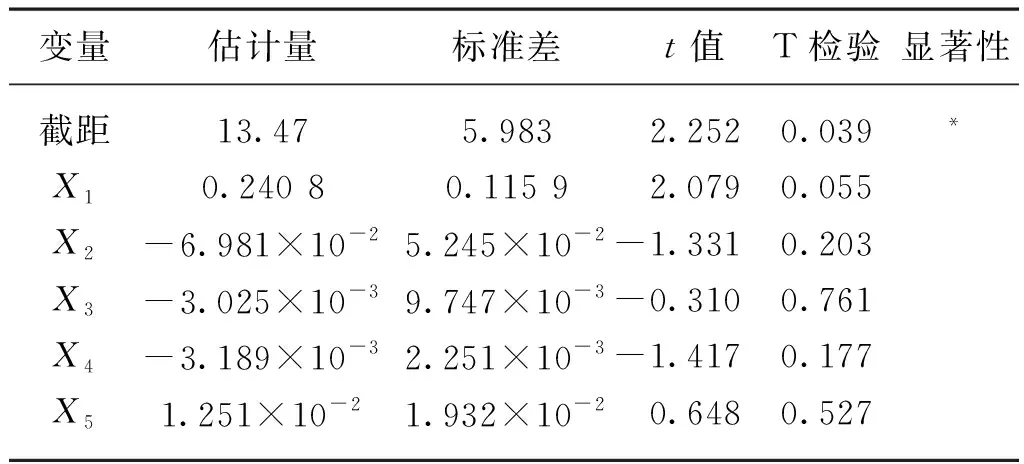
表3 多元線性回歸結果Tab. 3 Multiple linear regression results

由表3可知,在顯著性水平為0.05情況下,只有常數項的參數估計結果通過檢驗,X1～X5的參數估計結果未通過檢驗。X1、X5的參數估計結果為正值,故隨著X1、X5的增加,Y不斷增加;X2、X3、X4的參數估計結果為負值,故隨著X2、X3、X4的增加,Y不斷減小,這與相關性分析結果不符,造成上述情況最有可能的原因是未充分考慮自變量間的耦合性和多重共線性,從而使多元線性回歸分析結果失效。

方差膨脹因子是診斷變量多重共線性嚴重程度常用的方法之一,因此使用方差膨脹因子衡量多元線性回歸模型中各環境因子間的多重共線性。由多重共線性診斷結果可知所有變量的方差膨脹系數VIF均大于10,其中X1、X2、X4的方差膨脹系數高達1 352.66、526.64、458.69,說明溫室內環境因子間存在多重共線性,且空氣溫度、光照強度以及CO2濃度的多重共線性更為嚴重,說明空氣溫度、光照強度以及CO2濃度分別與不包括自身的其余四個變量間的耦合性較高,其余變量可用上述變量通過線性組合得到,猜想可用上述變量代替全部變量進行回歸分析。以空氣溫度為例,從實際情況出發,一般空氣溫度的升高或降低會直接影響其他變量的大小,如土壤溫度會隨空氣溫度的升高而升高,空氣濕度會隨空氣濕度的升高而降低等。多重共線性會導致一些嚴重后果;完全多重共線性會導致最小二乘法下的參數估計量不存在;近似共線性時會導致參數估計量的方差與協方差增大,使最小二乘參數估計量失效,進而導致參數區間估計不合理,并使得各解釋變量的t檢驗與方程的F檢驗失效[17]。故應選擇能夠解決多重共線性的回歸方法進行分析。

2.3 設施番茄果期生長模型構建

由多重共線性診斷結果可知環境因子間存在較為嚴重的多重共線性,在構建設施番茄果期生長模型時應該使用能夠處理多重共線性的建模方法。解決多重共線性的方法大致分為四類:第一類為添加懲罰項的嶺回歸、lasso回歸等;第二類為篩選變量的逐步回歸;第三類為重組主成分的偏最小二乘回歸和主成分回歸;第四類為神經網絡。由于本試驗數據較少,而神經網絡需要大量數據用于練習,因此先用最常見解決多重共線性的方法嶺回歸來構建設施番茄果期生長模型,分析果實橫徑與各環境因子間的關系,同時觀察嶺回歸分析結果是否有效。表4為嶺回歸分析結果。

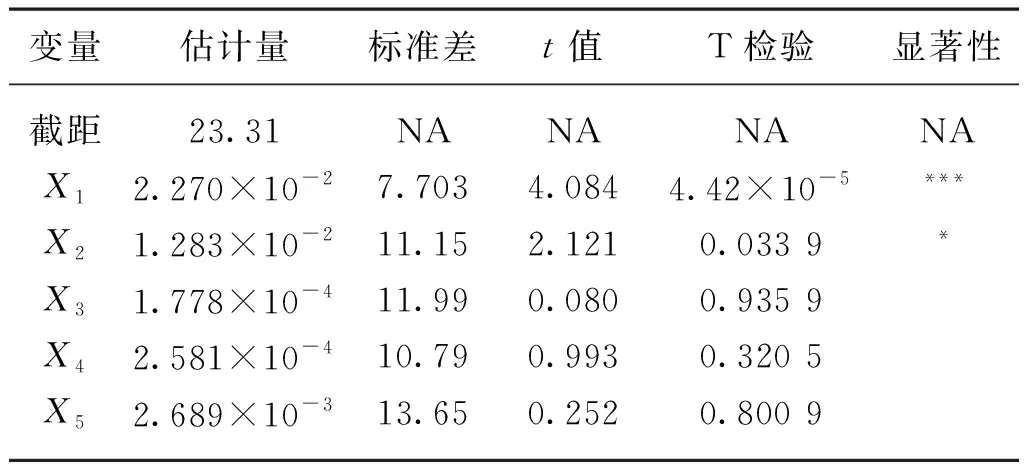
表4 嶺回歸分析結果Tab. 4 Ridge regression analysis results

由表4可知,在顯著性水平為0.05的情況下,X1、X2的參數估計結果通過檢驗,X3、X4、X5、Intercept的參數估計結果未通過檢驗,說明嶺回歸效果較差,故選擇其他解決多重共線性的回歸方法。逐步回歸的思路與嶺回歸完全不同,其基本思想是先用被解釋變量對每一個所考慮的解釋變量做簡單回歸,以貢獻最大的解釋變量對應的回歸方程為基礎,再逐步引入其余解釋變量。經過逐步回歸,最后保留在模型中的解釋變量既是重要的,又沒有嚴重多重共線性[18]。表5為對數據進行逐步回歸分析的過程。

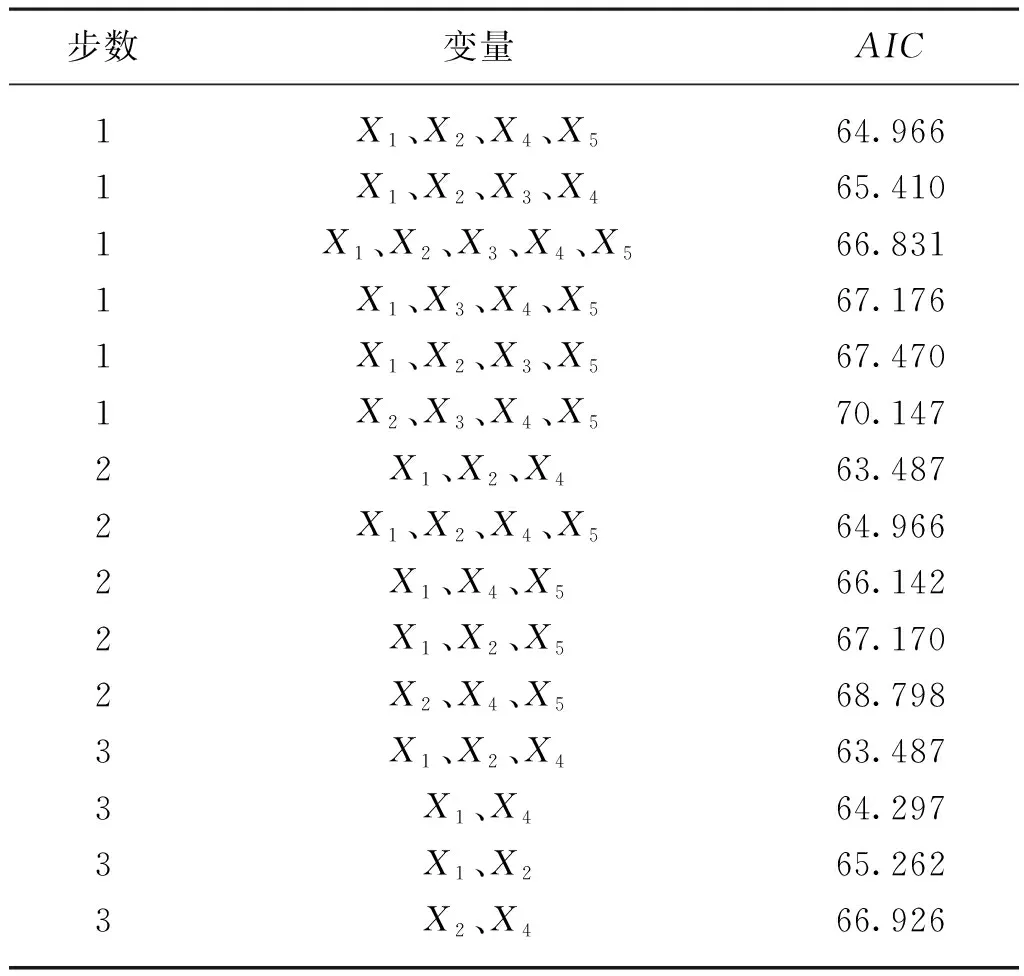
表5 逐步回歸分析過程Tab. 5 Stepwise regression analysis process

AIC(赤池信息準則)是一個運算退出的標志,當AIC值最小時運算退出。由表可知第一步在全部變量的基礎上除去一個變量進行回歸分析時AIC最小值為64.966,此時保留的變量為X1、X2、X4、X5,第二步在第一步基礎上除去一個變量進行回歸分析時AIC最小值為63.487,此時保留的變量為X1、X2、X4,第三步在第二步基礎上除去一個變量進行回歸分析時AIC最小值仍為63.487,保留的變量與第二步相同,此時AIC值最小,逐步回歸退出運算。

表6為對數據進行逐步回歸分析的結果。逐步回歸選取的最優自變量集為X1、X2、X4,由表6可知,在顯著性水平為0.05情況下,各變量的參數估計結果顯著性比嶺回歸分析明顯提高,但X2的參數估計結果仍未通過檢驗,且X2、X4的參數估計結果為負值,與相關性分析結果不符。逐步回歸通過選取變量初步解決了多重共線性問題,但是仍然存在分析結果與相關性不符、部分變量的參數估計結果未通過檢驗等問題。

表6 逐步回歸分析結果Tab. 6 Stepwise regression analysis results

主成分回歸是通過線性變換,將原來的多個指標組合成相互獨立的少數幾個能充分反映總體信息的指標,從而在不丟掉重要信息的前提下避開變量間共線性問題,便于進一步分析[19]。在主成分分析中提取出的每個主成分都是原來多個指標的線性組合。考慮將逐步回歸選取的變量進行主成分回歸分析,嘗試解決逐步回歸尚未解決的問題。

由主成分分析結果可知第一主成分Comp1的方差累計貢獻率為98.07%,第二主成分Comp2的方差累計貢獻率為99.97%,第三主成分Comp3的方差累計貢獻率為100%,由于Comp1即可解釋大部分變差,故用第一主成分進行回歸分析。現用Z1表示第一主成分,Z1為X1、X2和X4三個變量的線性組合且由主成分分析結果知Z1=0.583×X1+0.575×X2+0.574×X4,用Z1進行回歸分析的結果如表7所示。

表7 主成分回歸分析結果Tab. 7 Principal component regression results

由表7可知,第一主成分的參數估計結果為0.548 6,在顯著性水平為0.05情況下通過檢驗。根據主成分回歸分析結果知常數項可以忽略不計,回歸方程為Y=0.548 6×Z1,將Z1=0.583×X1+0.575×X2+0.574×X4代入Y=0.548 6×Z1,可得Y=0.319 8×X1+0.315 4×X2+0.314 9×X4,最后將回歸方程中的變量還原為原始變量,得到最終回歸方程為

Y=0.169 8×X1+0.012 15×X2+

0.000 557 7×X4+24.08

分析擬合方程可知X1、X2、X4的系數為正值符合相關性分析結果,解決了嶺回歸分析和逐步回歸分析不符合相關性分析結果、參數估計結果未通過檢驗的問題。

2.4 設施番茄果期生長模型評價與驗證

用逐步—主成分組合算法構建的設施番茄果期生長模型所有參數估計結果在顯著性水平為0.05情況下均通過檢驗,且全為正值,符合相關性分析結果。通過均方差、均方根和確定系數對模型進行評價,其中均方差為0.070 3,均方根為0.272 1,確定系數為0.929 7,模型誤差較小,擬合效果較好。取試驗第三批數據進行模型的驗證,圖2為模型驗證結果。

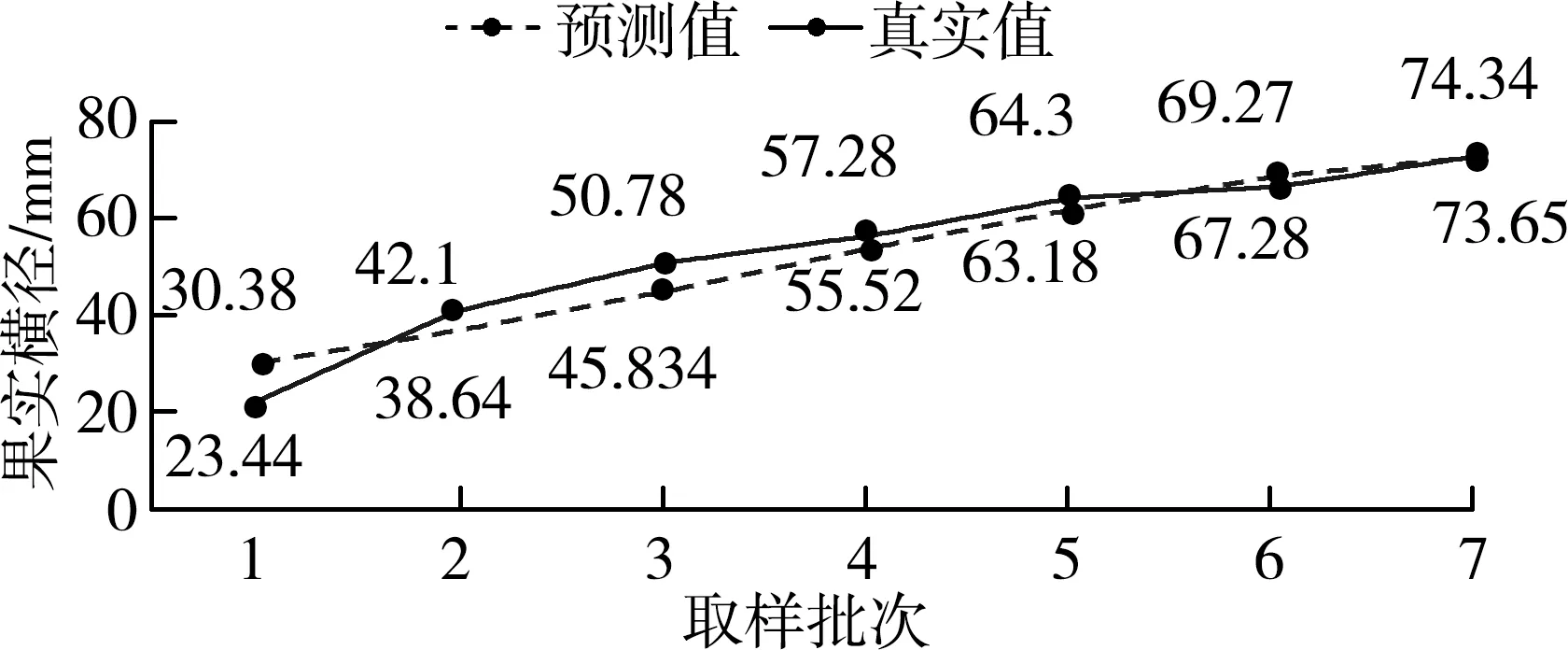
圖2 模型驗證結果Fig. 2 Model verification results

設施番茄果實自坐果期開始,橫徑和縱徑均隨生育進程的進行而不斷增大,呈“S”型曲線的變化規律,至成熟期達到最大值[12]。由圖2可知,設施番茄果期生長模型預測值比真實值更加平穩,因此前期誤差較大,后期誤差較小,總體來看擬合效果較好,能較好地表達溫室內環境因子與果實橫徑間的關系。

3 結論

本文以設施番茄果期為例,空氣溫度、空氣濕度、有效光輻射、CO2濃度、土壤溫度的累計量為輸入,果實橫徑為輸出,將前兩批數據用逐步回歸分析出顯著環境變量,然后進行主成分回歸構建設施番茄生長模型,用第三批數據驗證模型,解決了其他方法分析結果與相關性分析不符、部分參數估計結果未通過檢驗等問題。

1) 設施番茄結果期果實橫徑與空氣溫度、空氣濕度、有效光輻射、CO2濃度、土壤溫度存在較強的正相關性,相關系數分別為0.96、0.95、0.95、0.94、0.94。

2) 溫室內環境因子間存在較強的多重共線性,逐步回歸分析出顯著環境變量為空氣溫度、有效光輻射、CO2濃度。

3) 主成分回歸建立的設施番茄生長模型對果實橫徑的擬合效果較好,確定系數為0.93,能夠較好地表示果實橫徑與各環境因子間的關系。基于日光溫室內主要環境因子構建的設施番茄結果期生長模型,為設施番茄數字化的深入研究奠定了基礎。

本文通過試驗構建了設施番茄果期生長模型,但仍需要進行以下探索。未來工作可以考慮更換試驗場地或者控制環境變量單一驗證模型的有效性。本文只考慮了設施番茄果期,后續可以考慮設施番茄不同時期環境因子對番茄植株生長的影響。