融合波前邊緣檢測與快速搜索隨機樹的自主探索方法

張淑珍，馬玉祥，侯致遠，查富生，何 鎮

（1.蘭州理工大學 機電工程學院，蘭州 730000；2.哈爾濱工業大學 機器人技術與系統國家重點實驗室，哈爾濱 150001）

移動機器人已廣泛應用于工業、農業和軍事等領域。從搜索救援到行星探測[1]，未知環境下移動機器人自主探索成為機器人領域的研究熱點之一[2]。如何在時間短及路程少的條件下通過感知環境決定最佳探索目標點并移動至該點，進而完成移動機器人所在未知環境的遍歷，得到足夠的信息用于全局地圖創建[3]，是自主探索及地圖創建問題的核心，也是機器人實現真正自主，智能化的基礎性技術。

Umari H.[4]提出將快速搜索隨機樹（Rapid Random Tree,RRT）用于邊界檢測，并設計出局部RRT 前沿點檢測器與全局RRT 前沿點檢測器混合的搜索策略。金毅康[5]在傳統RRT 快速搜索隨機樹算法上，以其生長的端點作為廣度優先搜索（Breadth First Search,BFS）的起點搜索邊界點，從而提高邊界的獲取效率。Sun Xuehao[6]提出一種利用RRT 算法搜索邊界點，以距離代價、障礙物代價為判斷依據的性能指標函數，完成室外地面環境探索。RRT 算法偏向于覆蓋未知區域，雖然能夠實現探索邊界檢測的功能，但由于其生長具有隨機性，狹窄區域通過性較差，存在著邊界點提取不全面的問題，同時在提取邊界點或是樹枝生長過程中，需不斷檢查樹枝與障礙物及邊界之間的關系，一定程度上降低了邊界點提取的效率。Keidar M.[7]提出了兩種快速檢測邊界的方法，分別為快速前邊緣檢測（Fast Frontier Detector,FFD）與波前邊緣檢測（Wavefront Frontier Detector,WFD）算法，其中FFD方法只處理實時接收到的新激光數據，進行探索邊界的提取，同樣Sun Y.X.[8]等將柵格地圖與激光數據結合起來探索前沿區域，這種依賴于激光雷達數據的算法對傳感器硬件的精度有較高的要求，這在一定程度上限制了應用范圍，并且由于激光點在極端范圍內發散，此類算法提取激光數據構成的邊界輪廓時將跨越未知區域，難以覆蓋應被檢測為邊界的所有單元格。雖然Phillip[9]針對上述問題提出邊界跟蹤式邊界檢測（Frontier-Tracing Frontier Detection,FTFD）算法使用前一時刻邊界和傳感器包絡的端點作為當前時刻尋找新邊界的起點，提高了檢測邊界的準確性及完整性，但適用范圍還是受限于激光雷達的精度。WFD 方法則是只處理已經探索過的柵格地圖進行邊界的提取，在建圖前期具有較快的收斂速度，但隨著地圖的完備，需要遍歷的柵格數量變得龐大，使得邊界提取速度不斷上升，針對該問題Phillip[9]提出的擴展波前邊緣檢測（Expanding-Wavefront Frontier Detector,EWFD）算法在WFD 算法的基礎上對提取的邊界加入時間標簽，使用前一個時間步長的邊界作為起點，在未知環境中搜索邊界，減少了遍歷地圖柵格的數量，但其運行時間仍與已知區域大小成正比，且因時間標簽的加入而耗費大量的內存空間。

本文針對已有探索候選點算法提取耗時久、不全面，探索目標點引導機器人大角度轉向等問題，對傳統WFD 算法進行改進并與快速搜索隨機樹方法結合，分別作為局部候選點與全局候選點的提取方法。同時將螢火蟲算法輕簡化后，用于提取眾多探索候選點中的關鍵點，并在傳統評價函數中引入角度代價，提出一種基于改進的WFD 與RRT 融合的自主探索方法。

1 自主探索及地圖構建系統框架

未知環境下自主探索及地圖構建主要包括探索目標點的提取和地圖實時構建。自主探索算法提取探索目標點傳遞給定位導航算法，確定運動路線，采用SLAM 算法獲取感知傳感器的數據構建局部柵格地圖，隨著探索目標點的不斷生成，引導機器人遍歷環境，最終實現未知環境的全局地圖構建。自主探索及地圖構建系統如圖1 所示。

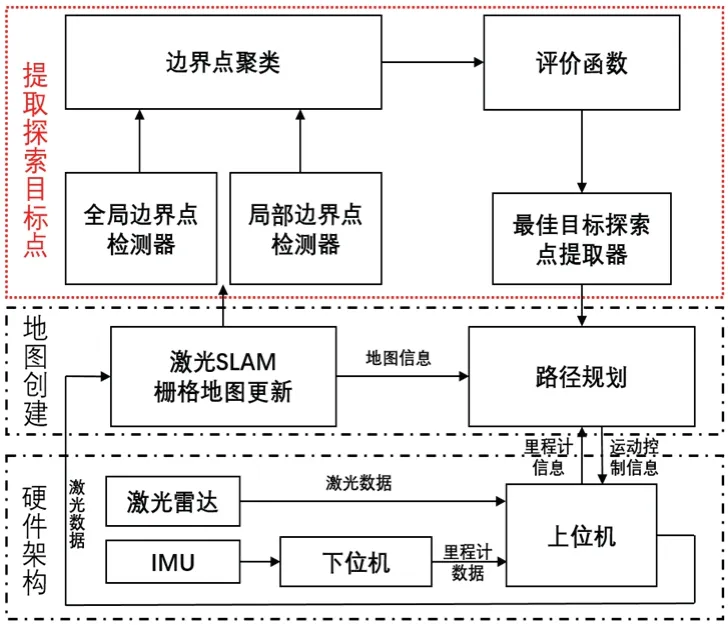
圖1 自主探索及地圖構建系統框圖Fig.1 System diagram of autonomous exploration and mapping

本系統利用ROS 平臺[10]編寫提取探索目標點模塊中的相關節點，即改進的WFD 局部候選點提取、RRT 全局候選點提取、輕量化螢火蟲聚類、改進的評價函數等。基于GMapping 算法接收激光雷達數據，用以構建二維柵格地圖，探索過程中利用ROS 集成的move_base 功能包獲取里程計信息和探索目標點，繼而進行路徑規劃[11]，不斷迭代直至探索完成。

2 探索候選點提取

2.1 基于改進波前邊緣檢測算法的探索候選點提取

Keidar M.[7]提出的傳統WFD（Wavefront Frontier Detector）算法只遍歷已探索的地圖，以機器人當前的位置為初始柵格利用廣度優先理論提取邊界點，通過檢測邊界點周邊相鄰單元格，快速提取邊界。該算法中存在三個隊列與一個集合，分別為待檢測隊列Qc、邊界點隊列Qp、邊界隊列Qf、邊界集合Sf{Qf1,Qf2,…,Qfn}，算法運行時將初始柵格Xr放入Qc中，搜索Qc中柵格的四鄰域，若不存在未知柵格，表示該柵格不是邊界點，將其四鄰域放入Qc中，不斷迭代，直至發現四鄰域存在未知柵格的邊界點，并將其放入Qp中，進而搜索Qp中邊界點的鄰域，將連續的邊界點存入Qf中，構成一條邊界，添加至Sf中。在建圖初始階段該算法確有較高的提取效率，但隨已探索區域擴大，Qc中儲存的元素增多，算法收斂時間不斷增加，且WFD 算法提取邊界時，需要為邊界點附上標簽以避免重復搜索同一邊界點，因此加劇了內存占用量，對于未知不確定區域范圍的搜索空間，如何在搜索區域擴大的情況下，保持較高的邊界點提取效率，是提高探索效率的前提。針對該問題，本文對傳統WFD 算法進行改進，通過限制搜索范圍并對邊界點歸類進行簡化操作以提高算法提取效率，將改進方法稱為WFD_L（Wavefront Frontier Detector Limit），改進思想如下：

(1)在Qc隊列元素篩選條件中加入距離條件。當搜索Qc中柵格的四鄰域不存在未知柵格，且滿足與初始柵格的歐式距離小于搜索閾值時，再將四鄰域柵格加入Qc中，以減少儲存元素的數量。圖2 為距離限制條件示意圖，圖中F、B 為WFD 算法搜索邊界點時所要遍歷的柵格，R 為當前機器人位置即初始柵格，ε為搜索閾值，可以看出B 的四鄰域柵格B1、B2、B3、B4的柵格狀態皆為空閑，且，可將B1、B2、B3、B4存入Qc中，而F 的四鄰域柵格雖然都不是未知柵格，但與初始柵格的距離大于ε，因此將F1、F2、F3、F4不存入cQ中。該策略使得WFD_L 算法在已探索區域增大的情況下仍然保持較低的收斂時間，提高邊界點提取效率。

(2)去除搜索Qp中元素鄰域，將連續的邊界點存入Qfn中，并添加至Sf集合的步驟，減少算法的計算量，降低主控單元計算負荷。

基于WFD_L 算法的候選點提取步驟如下：

步驟1：以機器人當前位置為初始柵格，利用四鄰域法判斷該柵格周圍柵格是否存在未知柵格，若不存在未知柵格則將其四鄰域放入待處理隊列中。

步驟2：若待處理隊列中存在數據，則檢測其中每一數據的四鄰域是否存在未知柵格，若存在則將其對應的數據移動到邊界點隊列，若不存在未知柵格，進行步驟3。

步驟3：判斷四鄰域柵格與機器人當前位置的距離，當小于一定閾值時，放入待處理隊列中。

步驟4：重復步驟2 與步驟3 直至待處理隊列中無元素存在，則表明機器人當前位置處的邊界點提取結束，返回邊界點隊列中的所有邊界點。

如圖3 所示為仿真環境下WFD 算法與WFD_L算法在探索地圖時提取邊界點所耗費時間對比，從圖中可以看出，WFD 算法迭代一次的時間隨著已知地圖的不斷擴大而持續增加，探索環境越大，則整體搜索效率隨著WFD 算法提取時間的上升而降低。而WFD_L 在提取邊界點時，通過距離條件改變柵格進入待處理隊列的規則使得遍歷范圍確定，將時間固定在2 ms 左右，不隨已知柵格的增多而上升。

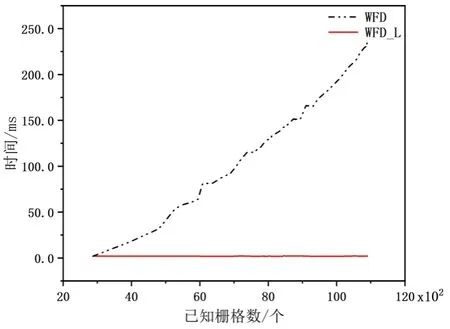
圖3 WFD 與WFD_L 提取邊界點消耗時間Fig.3 Time consuming of extracting frontier points by WFD with WFD_L

2.2 引入全局視角的探索候選點提取

基于WFD_L 算法提取局部候選點具有較高的效率，但未考慮全局最優，因此需融合一種具有全局視角的邊界點提取算法，避免機器人陷入局部陷阱。本文將搜索全局性、隨機性較好的隨機生成樹數據結構（RRT）[12]用于全局候選點提取。

融合算法提取候選點的步驟如下：

步驟1：初始化RRT 樹的根節點即機器人初始位置，使RRT 樹枝生長，同時啟用WFD_L 算法獲取局部候選點，最大化維持探索候選點提取的效率。

步驟2：若局部候選點數量大于某一閾值時，將其數據信息傳遞給聚類模塊進行處理，反之將RRT 生成的全局候選點信息傳遞給聚類模塊。

步驟3：若全局候選點與局部候選點不存在或小于某一閾值時表示地圖探索完成，停止自主探索并保存地圖。

3 最佳探索目標點選取

傳統最佳探索目標點提取，對所有邊界點進行評價函數處理，得到指標最優的邊界點作為探索目標點，增加了主控單元的計算負荷與算法收斂時間。為減少計算量，本文先對探索候選點進行聚類，再輸入評價模塊中，選出最佳探索目標點。

3.1 基于輕簡化螢火蟲算法的候選點聚類

常用的聚類算法有K 均值聚類、均值聚類及螢火蟲算法等。K 均值聚類需要提前知道類別數量，均值聚類則是尋找每一部分圓形滑動窗口中密度最大的中心點，無法適用于線性分布居多且無種類之分的邊界點。螢火蟲算法[13]通過自定的目標函數決定自身亮度，在邊界點聚類中可以將信息增益與路徑代價作為評價標準，更好地剔除每一區域較差的探索候選點，適用于線性分布較多的探索候選點聚類。但該算法無法保證自主探索的效率，針對該問題本文將螢火蟲算法嵌入自主探索系統，對大量探索候選點進行實時聚類時，建立目標函數并進行輕簡化處理，輕簡化思想如下：

(1)將邊界點的信息增益與路徑代價綜合考慮，構建螢火蟲算法的目標函數即自身光強I0如式(1)，其中0r表示當前候選點與機器人的距離，作為指數能夠避免路徑代價無限制地增大，γ為吸收系數，S 表示當前候選點的信息增益，其計算時以邊界點為圓心，傳感器測量距離為半徑，統計圓內的所有未知柵格的數量。

(2)將輕簡化螢火蟲算法的迭代次數設定為1，并保持感知范圍內最亮螢火蟲的位置不變，避免多次迭代導致探索效率下降，得到局部最優個體后，將剩余邊界點剔除，達到釋放緩存的同時，降低評價模塊的計算負荷。

輕簡化螢火蟲算法的運行步驟如下：

步驟1：計算群體中每一螢火蟲（候選點）的自身光強I0如式(1)。

步驟2：計算影響范圍內相比較的兩個螢火蟲之間的相對光強Ir，如式(2)，通過判斷Ir的大小殺死二者中相對光強較小的螢火蟲。

其中r表示相比較螢火蟲之間的距離。

步驟3：重復步驟2 遍歷搜索螢火蟲，最后返回存活的螢火蟲，作為聚類后的局部最優解。

如圖4(a)所示紅色邊界點是未經過輕量化螢火蟲算法聚類的邊界點，數量密集龐大，對評價函數的計算造成較大的負荷，而圖4(b)中黃色的邊界點是經過輕量化螢火蟲算法處理后的結果，在每一局部區域剔除影響因子較小的邊界點，保留相對最優的邊界點，在保證邊界信息完整性前提下，減少了控制單元不必要的計算量，提升最佳目標點的選取效率。

圖4 邊界點聚類前后對比Fig.4 Comparison of before and after frontier point clustering

3.2 具有角度代價的評價函數

評價函數通過計算每一探索候選點的探索收益，選擇最優值，確定最佳探索目標點。已有評價函數只包含信息增益與路徑代價，可以選出未知鄰域大且需行程少的探索點，但該點引導的運動趨勢可能與機器人當前姿態呈現較大夾角，致使機器人導航過程中頻繁旋轉，加劇導航成本，因此本文引入角度代價，即以機器人坐標系為基準計算最佳目標點與機器人位置連線的傾角，并與機器人當前姿態做差值，解決機器人因大曲率轉向導致探索低效的問題，本文稱之為評價函數_IDA（Information Distance Angular）。計算步驟如下：

步驟1：獲取機器人當前世界坐標系下的姿態，并計算機器人當前位置點與被評價候選點連線的傾斜角。

步驟2：分類討論傾斜角與機器人姿態之間的關系，確定出候選點與機器人姿態的角度差值。

如圖5 所示，直角坐標系O-xOy為機器人坐標系，P1,P2,P3,P4為各個象限中的任意候選點。處于機器人坐標系中第二、三象限的P2、P3點不能只通過與原點連線的斜率來計算相對機器人的偏轉角，需采用其補角作為相對機器人的偏轉角，因此將機器人姿態與候選點間的偏轉角關系進行分類討論。角度代價的計算公式為：

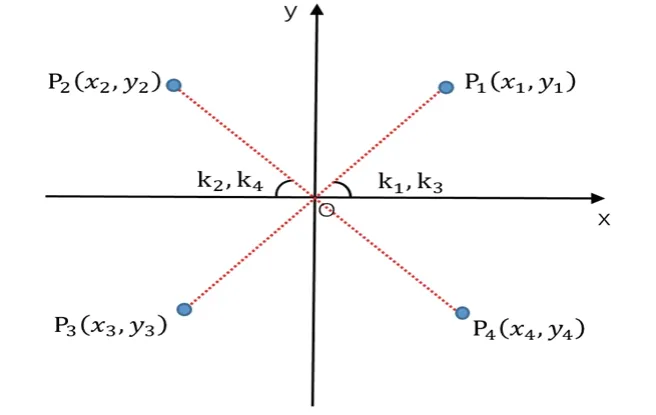
圖5 目標點相對機器人坐標系位置關系Fig.5 Position relationship of target points relative to the robot coordinate system

(a)當候選點處于坐標系的第一與第四象限時δ=0 ；(b)當候選點處于第二象限時δ=1 ；(c)當候選點處于第三象限時δ=-1，其中(xi,yi)為候選點坐標，(xr,yr)為機器人坐標，yaw為只考慮機器人繞z軸的姿態信息，其角度范圍為(0，π)與(0，-π)。

步驟3：對上述三種因素采用適宜的權重進行線性組合完成評價函數_IDA 的設計，評價函數計算公式為：

其中R為探索收益，μ,ε,τ為權重值，I為信息增益，d為距離代價，θ為角度代價。

4 仿真與實驗

4.1 最佳目標點選取實驗

為驗證角度代價對提高機器人探索效率的效果，在40 m×40 m 大小的仿真環境下進行了兩組實驗，其中候選點提取方法統一為傳統WFD 算法，目標點選取函數分別為傳統評價函數與評價函數_IDA。

雖然傳統評價函數能夠在探索過程中不斷產生目標點，直至結束，但由于該函數基于貪婪策略，選取每一目標點都是朝向未知區域最多，相對距離較近的邊界點，而沒有考慮機器人當前姿態，所以導致機器人在探索過程中多次大角度轉向，即機器人轉向目標點方位的角度大于π/2，從而降低探索效率，如圖6(b)黃色框線內就是機器人大角度轉向的運動行為。而評價函數_IDA 在考慮信息增益與路徑代價的基礎上選取目標點，控制機器人轉向角度，減少機器人大角度轉向，如圖6(a)顯示機器人的運動軌跡較為平滑，基本沒有大角度轉向運動行為，從而提高機器人在未知環境的探索效率。

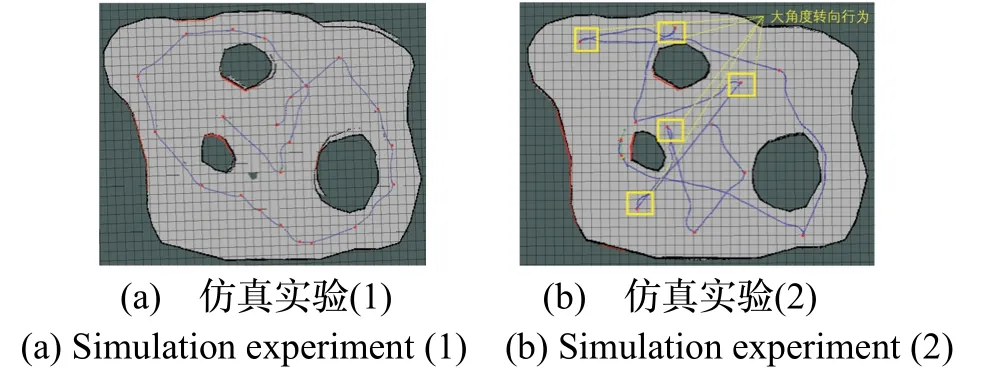
圖6 仿真實驗Fig.6 Simulation experiments

從圖7 可以看出，經過傳統評價函數提取后，有50%的目標點引導機器人進行大角度轉向；而經過評價函數_IDA 提取后，機器人大角度轉向的概率為10.00%，相比于傳統評價函數降低了38.89%。

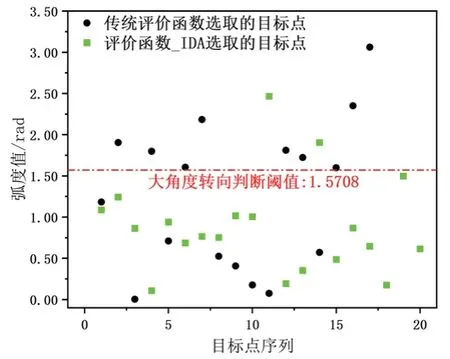
圖7 機器人轉向角分布圖Fig.7 Distribution of robot steering angle

為了消除實驗結果的偶然性，本文基于兩種評價函數在上述仿真環境下分別進行10 次目標點選取實驗，從轉向角、時間、路徑三方面比對評價函數_IDA與傳統評價函數的優劣，并計算對應平均值。如圖8(a)(b)為機器人大角度轉向占比與轉向角數據對比圖，圖8(c)(d)為自主探索過程中耗費時間與行進路程對比圖。

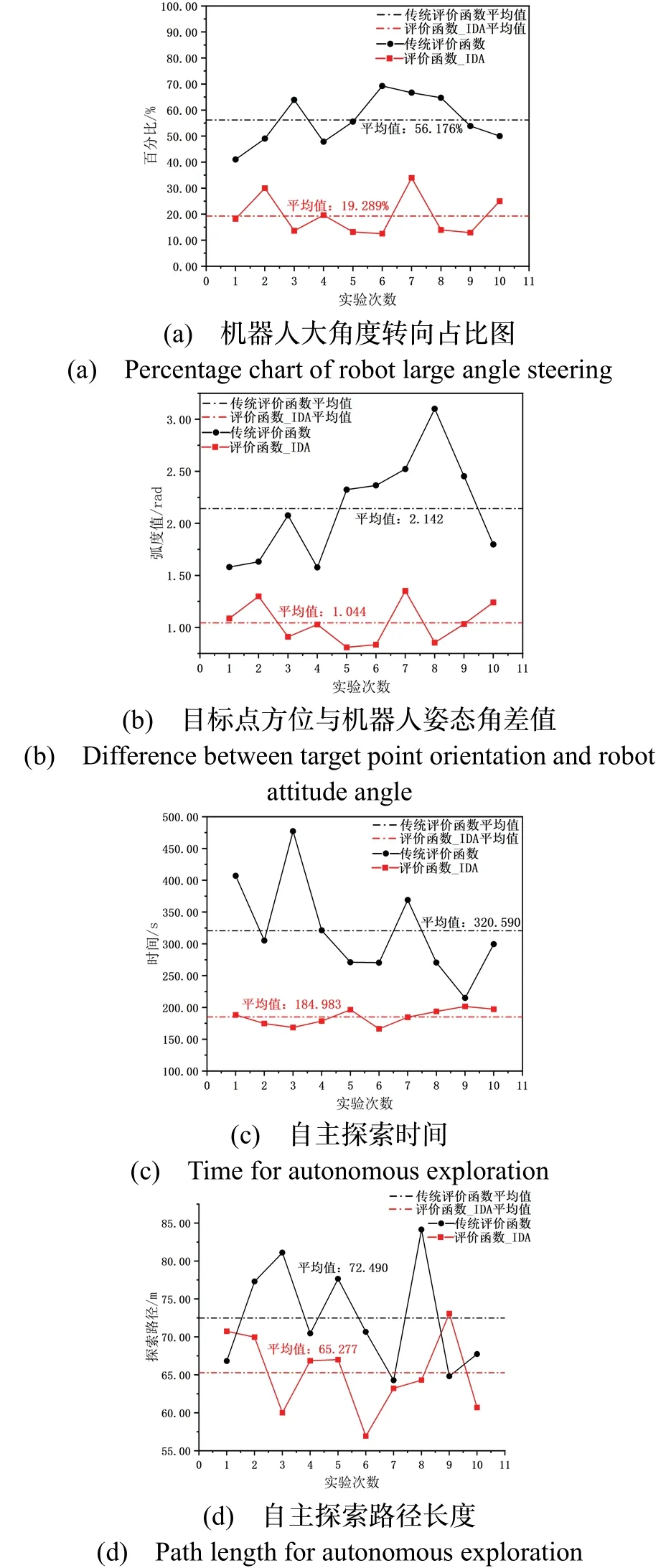
圖8 仿真結果對比Fig.8 Comparison of simulation results

從圖8(a)(b)可看出，傳統評價函數選取的目標點引導機器人轉向的平均角度為2.142 rad，大角度轉向占比為56.18%，評價函數_IDA 選取的目標點引導機器人轉向平均角度為1.044 rad，相比于傳統評價函數減少了1.098 rad，大角度轉向占比為19.29%，相比于傳統評價函數降低了36.89%。從圖8(c)(d)可看出，機器人考慮角度代價后，探索時間節省了42.30%，路徑長度縮減了9.95%。綜上所述，證明了加入角度代價的評價函數（評價函數_IDA）對于提升地圖創建效率的有效性。

4.2 自主探索實驗

為驗證本文提出的自主探索算法的整體性能，且剔除結果的偶然性，在如圖9(a)面積約為50 m2的真實環境下，使用如圖9(b)控制單元為Jetson nano，搭配有鐳神N10 激光雷達的樣機進行了5 次實驗。該實驗將Keidar M.[7]提出的WFD 算法、金毅康[5]提出的RRT-BFS 算法與本文提出的WFD-RRT 算法從探索時間、路徑長度兩方面進行比對分析。

圖10(a)為機器人在初始位置探索到的柵格地圖，圖10(b)為探索過程中生成的柵格地圖，圖10(c)為最終建圖的結果，可以看出該算法能夠引導機器人在未知環境中建立完整的地圖，為防止劇烈碰撞，將機器人最大速度限制為0.1 m/s。從表1 可看出，WFD-RRT算法相較于WFD 算法，探索路徑長度增加約2.95%，探索消耗時間降低約38.24%，這表明WFD-RRT 算法沒有陷入局部陷阱而往復徘徊，反而通過降低候選點提取的計算量，減少地圖創建時間，提高了自主探索效率；WFD-RRT 算法相較于RRT-BFS 算法，探索路徑長度減少約32.13%，探索消耗時間降低約22.19%，總體來看，WFD-RRT 算法能夠較明顯地提升未知環境自主探索效率，在探索候選點提取、最佳目標點選擇方面都有一定的優勢，驗證了WFD-RRT 算法的可行性與有效性。

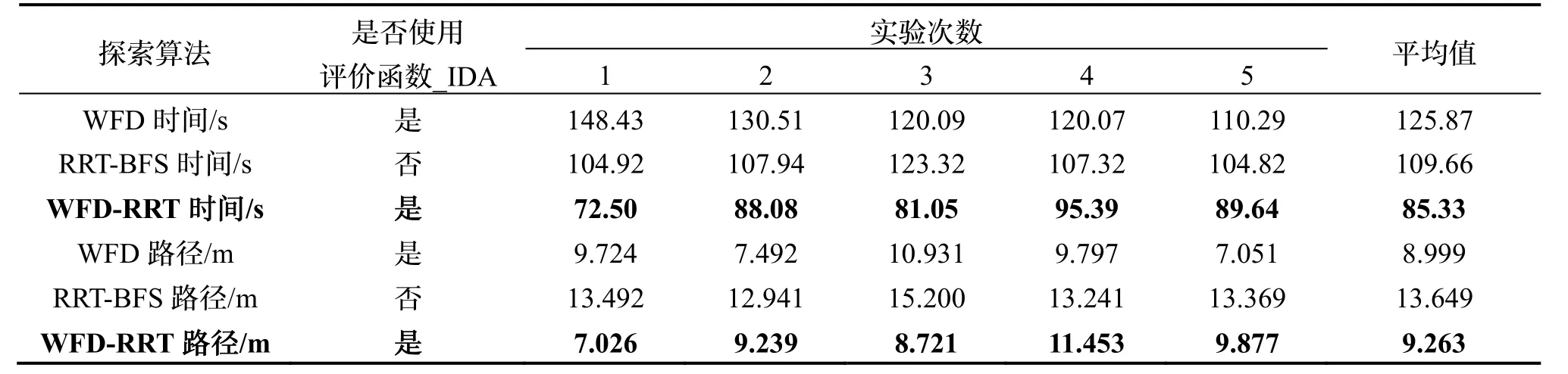
表1 樣機實驗結果對比Tab.1 Comparison of prototype experimental results

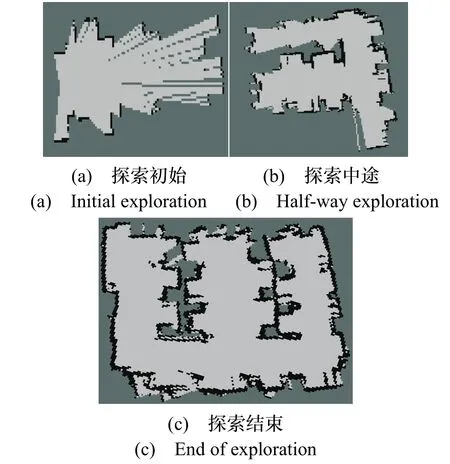
圖10 自主探索過程Fig.10 Process of autonomous exploration

5 結論

本文以提高自主探索效率為目標，針對候選點提取與聚類、目標點選取，提出一種基于WFD_L 與RRT融合的自主探索方法。通過仿真與實驗測試結果，得出以下結論：

(1)提出一種考慮方向的評價函數，仿真實驗得出評價函數_IDA 相比于傳統評價函數選取的探索目標點，引導機器人大角度轉向的概率下降36.89%，探索路徑與探索耗時分別減少9.95%、42.30%。表明引入角度代價的評價函數_IDA 相比于傳統評價函數能夠提取出更高效的探索目標點。

(2)提出的WFD-RRT 算法，通過限制WFD 算法的搜索范圍，并在傳統評價函數中引入角度代價，使得探索候選點提取時間縮短、目標點選取更有效。在實驗環境中，該算法的探索路徑及探索耗時相比于RRT-BFS 算法分別降低了32.13%、22.19%，表明WFD-RRT 算法具有更加高效的探索效果。