Thermodynamic limit of the XXZ central spin model with an arbitrary central magnetic field

Fa-Kai Wen(溫發(fā)楷) and Kun Hao(郝昆)

1College of Physics and Electronic Information,Yunnan Normal University,Kunming 650500,China

2Yunnan Key Laboratory of Opto-Electronic Information Technology,Kunming 650500,China

3State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Wuhan Institute of Physics and Mathematics,Chinese Academy of Sciences,Wuhan 430071,China

4Institute of Modern Physics,Northwest University,Xi’an 710127,China

5Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China

6Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China

Keywords: integrable spin chain,Bethe ansatz,T–Q relation,central spin model,thermodynamic limit

1.Introduction

The central spin or Gaudin model[1]describes a single spin coupled to a bath of spins (see Fig.1), and has played an essential role in condensed matter physics,[2,3]ultracold atoms,[4]quantum optics and quantum information.[5–9]The Hamiltonian of theXXZcentral spin model with an arbitrary central magnetic fieldBreads

For theθ=0 case,the eigenvalues and eigenstates of the Hamiltonian(1)can be exactly solved by the algebraic Bethe ansatz method.[16,17]Based on the exact solutions,on the one hand, an efficient technique has been devised for the numerical solution of the Bethe ansatz equations (BAEs);[18]on the other hand, the thermodynamic limit of the models is a subject of intense research.[19–23]For theθ/=0 case, the integrability and solutions of the model have been studied when

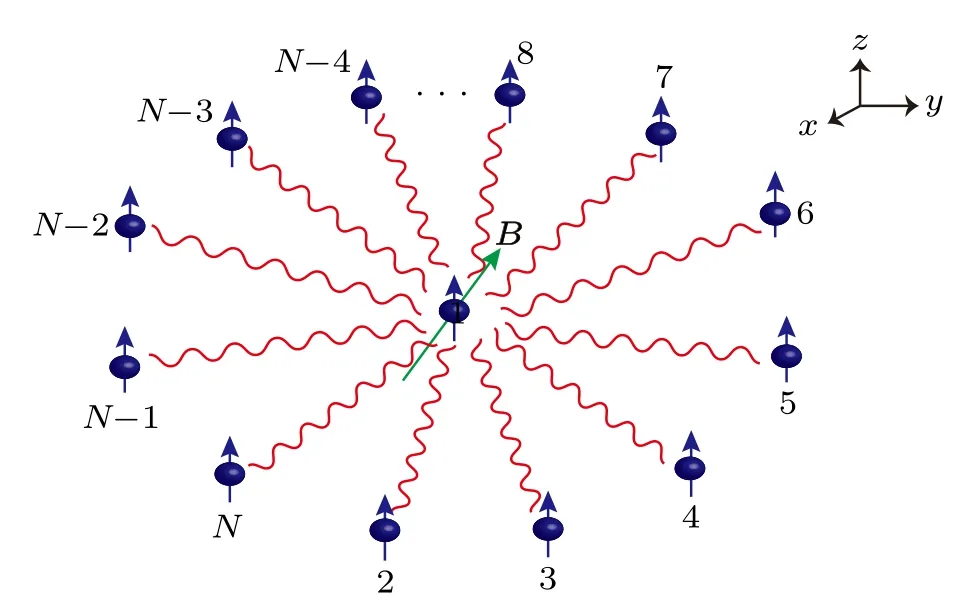
Fig.1.The XXZ central spin model with an arbitrary central magnetic field B.

Inthis paper, weconsiderthe coupling constantAk=,andΔk=.In thiscase,themodelis integrable.By using the off-diagonal Bethe ansatz(ODBA)method,[26,27]we derive the energies,eigenstates and Bethe ansatz equations of the model.In addition,we give numerical evidence that the whole spectrum and eigenstates are obtained by the ODBA method.Using the energies and Bethe ansatz equations, we study the thermodynamic limit of theXXZcentral spin model with an arbitrary central magnetic field.It is found that the contribution of the inhomogeneous term in the associatedT–Qrelation to the ground state energy satisfies anN-1scaling law,whereNis the number of spin particles.This fact enables us to investigate the properties of the system whenNtends to infinity.By assuming the structural form of the Bethe roots forN →∞,we calculate the contribution of the direction ofBto the ground state energy,i.e.,Eθ=r(1-|cos(θ)|).For ther/=0,θ/=0, andθ/=πcase, the contribution of the direction of the central magnetic field does not reduce to zero whenN →∞.

The paper is organized as follows.We derive the Bethe ansatz solutions of theXXZcentral spin model with an arbitrary central magnetic field in Section 2.In Section 3,we focus on the contribution of the inhomogeneous terms to the ground state energy.In Section 4, based on the finite-size effects of the system, we study the thermodynamic limit of the model.We summarize and discuss our results in Section 5.

2.Bethe ansatz solutions

2.1.Integrability of the model

The integrability of the Hamiltonian(1)is associated with the rationalR-matrix

whereuis the spectral parameter,ηis the crossing (quasiclassical)parameter,andPis the permutation operator

Here and below,we adopt the standard notation: for any operatorO ∈End(V),Ojis an embedding operator in the tensor spaceV ?V ?···, which acts asOon thej-th space and as an identity on the other factor spaces;Ri,j(u)is an embedding operator of theR-matrix in the tensor space,which acts as an identity on the factor spaces except for thei-th andj-th ones.

TheR-matrix satisfies the Yang–Baxter equation[28,29]

and possesses the following properties:

Hereρ(u) = (u+η)(u-η),V=-iσy,R2,1(u) =P1,2R1,2(u)P1,2.=(1/2){1?P1,2}is the antisymmetric(symmetric) projection operator in the tensor product spaceV ?V.The subscriptt2denotes the transpose in the 2nd quantum space.

In this paper,we consider the reflection matrixK-(u),

which satisfies the reflection equation(RE)

and the general non-diagonal matrixK+(u),

which satisfies the dual RE

The parameters ˉξandh2can depend on the crossing parameterη.Expanding ˉξandh2with respect toη, we have the following expressions:

To describe the system, we introduce the one-row monodromy matrices

and the double-row monodromy matrix

Here,{εj,j=1,...,N}are the inhomogeneous parameters.The transfer matrix is given by

where tr0denotes the partial trace in auxiliary space.Following the same procedure as in Ref.[10], one can obtain the commutativity of the transfer matrices with different spectral parameters

This ensures the integrability of the model described by the Hamiltonian(1).The Hamiltonian(1)can be obtained by

The central magnetic fieldBin the Hamiltonian is described by the parameters in theK-matrices(10)and(12)

2.2.Energy spectrum and Bethe ansatz equations

In our current model, theK-matricesK-(u) (10) andK+(u) (12) do not commute.This leads to the fact that they cannot be diagonalized simultaneously (corresponding to the arbitrary central magnetic field).Therefore there is no obvious reference state of the system.The standard algebraic Bethe ansatz cannot be performed on this model.With the help of the ODBA method,[26]we construct the inhomogeneousT–Qrelation

where the functionQ(u) is parameterized byNparameters{λj|j=1,...,N}

and the functions ˉa(u), ˉd(u),F(u)and the constantcare given by

Based on the construction of the Hamiltonian equation(23),the energy spectrum can be derived from Eq.(25),

and the Bethe roots{λk|k=1,...,N}need to satisfy a set of Bethe ansatz equations(BAEs)

The numerical solutions of the BAEs (32) and the corresponding eigenvalues (energy spectrum) and eigenstates of the Hamiltonian (1) forN=4 are shown in Table 1.These numerical simulation results show that the BAEs(32)give the complete spectrum and eigenstates of theXXZcentral spin model with an arbitrary central magnetic fieldB.

Table 1.Solutions of BAEs(32)for the case of N=4,{εk =exp(1-(k-1)/N),k=1,2,...,N},r=θ =π/4,φ =π/3.The symbol n indicates the number of eigenvalues, and En is the corresponding energy.The energy En calculated from Eq.(31)is the same as that from the exact diagonalization of the Hamiltonian(1).

Table 1.Solutions of BAEs(32)for the case of N=4,{εk =exp(1-(k-1)/N),k=1,2,...,N},r=θ =π/4,φ =π/3.The symbol n indicates the number of eigenvalues, and En is the corresponding energy.The energy En calculated from Eq.(31)is the same as that from the exact diagonalization of the Hamiltonian(1).

λ1 λ2 λ3 λ4 En n 2.5340-0.0000i 5.2448+0.0000i 3.2728-4.3238i 3.2728+4.3238i -8.5582 1 2.5378-0.0000i 3.3617+0.0000i 0.0000+7.1505i 0.0000+0.0391i -7.6410 2 0.0357-0.0000i 2.4464+0.0000i 0.0000+7.0824i 0.0000+3.2666i -7.1886 3 1.4347-0.0000i 2.3655-0.0000i 0.0000+7.1202i 0.0000+0.5340i -6.7823 4 0.0000+7.1044i 0.0000-0.7655i 1.7426-0.1557i 1.7426+0.1557i -2.3488 5 0.0459+0.0000i 1.8551+0.0000i 0.0000+3.9170i 0.0000+6.9857i -0.2465 6 0.0779+0.0000i 1.4048+0.0000i 0.0000+4.3178i 0.0000+6.9018i 0.8440 7 1.8758-0.0000i 4.5410-0.0000i 0.0000+7.2122i 0.0000+0.0435i 1.4610 8 0.0000+1.5783i 0.0000+0.0261i 0.1361-6.0292i 0.1361+6.0292i 2.2401 9 1.4116-0.0000i 4.8134-0.0000i 0.0000+7.2495i 0.0000+0.0862i 2.3642 10 1.9223+0.0000i 5.1640-0.0000i 3.0613-3.7809i 3.0613+3.7809i 2.6470 11 0.0208-0.0000i 5.4871+0.0000i 0.0000+7.4128i 0.0000+1.9644i 3.5101 12 1.4507+0.0000i 4.9474-0.0000i 2.9169-3.2725i 2.9169+3.2725i 3.8581 13 0.0000+0.0164i 0.0000+4.3452i 4.8658-1.8970i 4.8658+1.8970i 4.5956 14 0.0159-0.0000i 5.3534+0.0000i 3.3592-3.4663i 3.3592+3.4663i 4.7109 15 7.5242-10.0807i 7.5242+10.0807i 11.2114-3.3813i 11.2114+3.3813i 6.5345 16

3.Finite-size effects

From now on, we consider the system withAk ＞0 andΔk ＞0.This corresponds to the parameter configuration{ε1＞εi ＞0,i=2,...,N}or{ε1＜εi ＜0,i=2,...,N}.From Eqs.(31) and (32), one can conclude that{ε1＞εi ＞0,i=2,...,N}is equivalent to{ε1＜εi ＜0,i=2,...,N}for the system.For the homogeneous cases,we haveε2=ε3=···=εN.For the inhomogeneous cases, without loss of generality,we assumeε1＞ε2＞ε3＞···＞εN ＞0.

From Eqs.(31) and (32), we know that the parameterφmakes no contribution to the energy expression.Therefore,let us setφ=0,and the Hamiltonian becomes

Forθ ∈[0,π/2],the Hamiltonian possesses the property

3.1.The θ =0 case

For theθ=0 case,the total spin in thez-direction is conserved.The energy spectrum is

and the associated BAEs are as follows:

The system is a single spin coupled toN-1 bath spins by inhomogeneous antiferromagnetic couplings (Ak ＞0 andΔk ＞0).The numerical solutions of BAEs (36) and the corresponding eigenvalues(full energy spectrum)of the Hamiltonian(1)forN=3 are shown in Table 2.We also give the numerical solutions of the ground state energy for larger system sizes (N=4, 8, 12, 16, 20, 24), in Table 3.One can obtain the lowest energy state in the subspaceM=1 and a certain range of Bethe root.[30–32]For the ground state of the system,the BAE is

The left hand side of BAE (37) has a finite value for a finiterand a nonzeroλ.This indicates that the right hand side of BAE (37) also has a finite value whenNis a finite value orN →∞.TakingN →∞for Eq.(37),{λ →εk,k=1,2,3,...,N-1}should be the Bethe roots.Thus,in the thermodynamic limit, we can assumeλ=εk-δkandδk ＞0.It is obvious that the system has the least energy whenλ →ε1.Substitutingλ=ε1-δinto Eq.(37),we obtain

Noting thatδ →0 whenN →∞,one can obtain

To keep the equality,ε1-εkmust be greater than 2δ.Making the series expansion for,we get

Forl=1,one can obtain

Table 2.Solutions of BAEs (36) for the case of N =3, {εk =exp(1-(k-1)/N),k=1,2,...,N},r=2,θ =0.The symbol n indicates the number of eigenvalues, and En is the corresponding energy.The energy En calculated from Eq.(35)is the same as that from the exact diagonalization of the Hamiltonian(1).

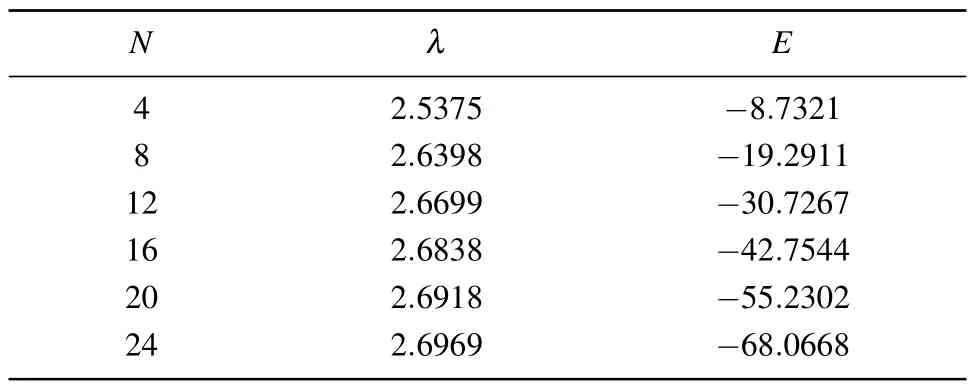
Table 3.Solutionsof BAEs(36) forthecase of {εk =exp(1-(k-1)/N),k=1,2,...,N},r=2,θ=0.Thesymbol λindicatesthe Bethe root of the ground state,and E is the corresponding energy.The ground state energy E calculated from (35) is the same as that from the exact diagonalization of the Hamiltonian(1).

3.2.The θ /=0 case

For theθ/= 0 case, theU(1) symmetry of the system is broken.The corresponding BAEs (32) obtained from the ODBA method have a much more complicated structure,which makes it difficult to approach the thermodynamic limit of the model.On this question, we have made some progress.[30,31]To study the contribution of the inhomogeneous term (the last term of Eq.(25)) to the ground state energy, we first consider theT–Qrelation without the inhomogeneous term,i.e.,

The functionQ(u)is parameterized byMparameters{λj|j=1,...,N}

Using the same procedure,we obtain

We remark that, for a finiteNandθ/=0, ～Eis different from the exact eigenvalueEgiven by Eq.(31).To study the difference between ～EandE,we define

The ΔEis the contribution of the inhomogeneous term in the associatedT–Qrelation to the energy spectrum.

Fig.2.The contribution of the inhomogeneous term to the ground state energy ΔE versus the spin particles N.The data can be ftited as ΔE=γNβ[or ln(|ΔE|)=pln(N)+q].Here r=3,{εk=exp(1-(k-1)/N),k=1,2,...,N}, φ = 0, (a) θ = π/4, γ = 0.5955 and β = -0.9633; (b)θ =π/2, γ =2.0470 and β =-1.1350.Due to the fact that β ＜0 [or p ＜0],when N tends to infinity,the contribution of the last term tends to zero.

Similar to theθ=0 case,for the ground state of the system,we haveM=1 and the BAE becomes

The values of ΔEversus the number of spinsNare shown in Fig.2.It indicates a power law (N-1scaling law) (Based on the previous works,[30–32]we know that the contribution of the inhomogeneous term to the energy can have power decay or exponential decay, whenNtends to infinity.In our current work,the contribution of the inhomogeneous term to the energy has power decay ΔE=γNβ, (β ≈-1),N →∞.We call it theN-1scaling law.) relation between ΔEandN, i.e.,ΔE=γNβ.Asβ ≈-1, the value of ΔEtends to zero whenN →∞.Thus,we can study the properties of the system in the thermodynamic limit via the BAE(47).

It is obvious that{λ →εk|k=1,2,...,N}should be the Bethe roots forN →∞.From Eq.(44),the system has the least energy whenλ →ε1.Substitutingλ=ε1-δ′into Eq.(47),we have

Considering thel=1 case,one can obtain

4.Contribution of θ to the ground state energy

In order to study the contribution of the direction of the central magnetic field to the ground state energy,we define

Then we have

in both the homogeneous and inhomogeneous cases.Considering the Hamiltonian possesses the property(34),one can obtain

For ther/=0,θ/=0 andθ/=πcase,the direction of the central magnetic field contributes nonzero values to the ground state energy in the thermodynamic limit.By using the relation (52), one can calculate the contribution of the direction of the central magnetic field to the ground state energy.The results are shown in Fig.3,where the lines are the energyEθcalculated by using the relation (52) and the green stars are data obtained by employing the BST algorithms[33]to solve the energyEθof the Hamiltonian (1) in the thermodynamic limit.Specifically,for one of the green stars,we first calculate the ground state energyEg(N) withN=4,...,24 by numerical diagonalization.Then, the large-Nextrapolation of the energyEg(N)was performed using BST algorithms from the sequence ～Eg(4)-Eg(4), ～Eg(6)-Eg(6),..., ～Eg(24)-Eg(24).From Fig.3, we can see that the analytical and numerical results agree with each other very well.

Fig.3.The energy spectrum Eθ versus the parameter θ.The curves are calculated from Eq.(52),while the green stars are obtained from the Hamiltonian(1)with the BST algorithms.Here(a)ε1 =1.8,ε2 =εN =0.7;(b)εk=exp(1-(k-1)/N),k=1,2,...,N.

The integrable models withU(1) symmetry breaking caused by the direction of magnetic fields can be divided into two categories:One is where the model has a special direction,and the external magnetic field does not follow that direction(see Fig.1); the other is the model with unparallel boundary magnetic fields(see Fig.4).For the first category,the contribution of the direction of the magnetic field to the ground state energy is a finite value.[34–36]For the second category,the contribution of the relative angle between the boundary magnetic fields to the ground state energy reduces to zero in the thermodynamic limit.[30,31]

Fig.4.The model with unparallel boundary fields.

From the point of view of theT–Qrelation, when the parameters reflectingU(1)symmetry breaking only appear in the inhomogeneous terms, theU(1) symmetry breaking does not affect the properties of the system in the thermodynamic limit if the inhomogeneous terms can be ignored under the limit.However,when the parameters reflectingU(1)symmetry breaking appear in both the homogeneous and inhomogeneous terms,the effect ofU(1)symmetry breaking still exists in the thermodynamic limit even if the inhomogeneous terms can be ignored in the limit.

5.Conclusion

In this paper, by using the off-diagonal Bethe ansatz method, we have presented the energy spectrum (31) and Bethe ansatz equations(32)of the model.In addition,we have given numerical evidence that the whole spectrum and eigenstates are obtained by the off-diagonal Bethe ansatz method.

Using the energies(31)and Bethe ansatz equations(32),we have studied the thermodynamic limit of theXXZcentral spin model with an arbitrary central magnetic field.It is found that the contribution of the inhomogeneous term in the associatedT–Qrelation to the ground state energy satisfies anN-1scaling law,whereNis the number of spin particles.This fact enables us to explore the properties of the system in the thermodynamic limit.By assuming the Bethe rootsλ=εk-δk,the contribution of the direction ofBto the ground state energy is given byEθ=r(1-|cos(θ)|).For ther/=0,θ/=0 andθ/=πcase,the contribution of the direction of the central magnetic field is a nonzero value.Our work provides a simple and powerful tool to study the thermodynamic limit of the integrable model withoutU(1)symmetry.

Acknowledgments

The authors would like to thank Prof.X.-W.Guan for valuable discussions.Project supported by the National Natural Science Foundation of China (Grant Nos.11847245,11874393, and 12134015), the Doctoral Scientific Research Foundation of Yunnan Normal University (Grant No.00900205020503180), the National Natural Science Foundation of China (Grant Nos.12275214, 11805152,12047502, and 11947301), the Natural Science Basic Research Program of Shaanxi Province(Grant Nos.2021JCW-19 and 2019JQ-107),and the Shaanxi Key Laboratory for Theoretical Physics Frontiers in China.