Quantum correlation enhanced bound of the information exclusion principle

Jun Zhang(張鈞), Kan He(賀衎), Hao Zhang(張昊), and Chang-Shui Yu(于長水)

1College of Data Science,Taiyuan University of Technology,Taiyuan 030024,China

2College of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China

3College of Information and Computer,Taiyuan University of Technology,Taiyuan 030024,China

4School of Physics,Dalian University of Technology,Dalian 116024,China

Keywords: quantum correlation,information exclusion principle,entropic uncertainty relation

1.Introduction

Quantum information theory is an important tool to deal with all kinds of the quantum problem[1]and is widely used in various quantum information processing tasks, such as quantum key distribution, quantum cryptography, and entanglement witness.[2–20]Measurement plays a vital role in quantum theory.It is the interface between the classical world and the quantum world,which is characterized by noncommutativity and superposition.However, for any given measurement,superposition and noncommutativity necessarily lead to uncertainty in the outcomes of measurements.Simultaneously,it produces another critical quantity, information.From the viewpoint of quantum information,Shannon entropy could be used to quantify the amount of uncertainty about the observables.Deutsch[21]quantified uncertainty in terms of Shannon entropy and derived the entropic uncertainty relation for any pair of observables.[22]It describes the limitations of our ability to simultaneously predict the measurement outcomes of non-commuting observables in quantum theory.Later, Kraus conjectured the improved result.[23]Maassen and Uffink[24]gave the tighter entropic uncertainty relations:

whereH(X) (H(Y)) is the Shannon entropy of measurement outcomes when a measurement of observableX(Y)is performed on a stateρ, andc= maxi,j|〈xi|yj〉|2quantifies the complementarity of the non-degenerate observablesXandYwith|xi〉,|yj〉denoting their eigenvectors, respectively.Subsequently, the entropy uncertainty relation has been extensively studied.[25–39]Based on the accessible information about a quantum system represented by an ensemble of states,Hall first generalizes the bound of the information exclusion principle.[40]Suppose that for the quantum ensemble{pi,ρi},the corresponding quantum state formula isρε=∑i piρi,subject to the mutual information corresponding to the measurement ofAon the quantum stateρε, then we haveI(A|ε)=S(A|ρε)-∑i piS(A|ρi),whereS(A|ρ)is the associated entropy defined asS(A|ρ)=-∫dap(a|ρ)logp(a|ρ).For observablesΠi,(i=1,2,...,N),Hall proposed the general form inequalities for the information exclusion principle

with the nontrivial quantum boundJ.It implies that for any selected observables the information gain can be maximized at the expense of the observables’complementary.

Acting as the best-known information exclusion principle, it has not been studied as much as quantum uncertainty relations.[41,42]Subsequently,Grudkaet al.considered the observablesXandYthat are performed on system A,andZis a classical register that may be correlated to A.They improved the bound and conjectured a stronger information exclusion relation[43]

with the quantum mutual informationI(X(Y):Z)and the sum over the largestdterms of the matrix|〈xi|yj〉|2.In what follows,we describe a stronger version of the information exclusion principle,proved by Coles and Piani,that can also be extended to the much more general case of quantum memory.[44]

whereH(A|B)=H(ρAB)-H(ρB)is the quantum conditional entropy and(Π, ～Π)stands for(X(Y),Y(X)).In addition,they further explained the distinction between the complementarity of uncertainty and the complementarity of information.Namely, to obtain a state-independent bound for uncertainty relations.It must consider the subspace with the least complementarity whilst concerning the various subspaces that compose the space, i.e., it is the overall complementarity, and it formulates the information exclusion relations.In other words,for uncertainty relations,a trivial bound will be generated whilst the information exclusion principle will be a nontrivial bound.Considering the multiple measurements,Zhanget al.gave the quantum memory-assisted information exclusion principle as[45]

where

However,the above model focuses on the bipartite quantum state for multiple measurements.It means that one part is the measured subsystem which is measured by multiple measurements, and the other part is the quantum memory which can store measurement information.Thus, it will be interesting to find out the information exclusion principle in multiple quantum states for multiple measurements.Inspired by the ideas of monogamy or decoupling which is close to quantum cryptography, in this paper we would like to split the quantum memory intoNparts compared to the bipartite quantum state, and present multiple quantum memory-assisted information exclusion principle for multiple measurements.It is found that the upper bound includes the complementarity of the observables,quantum discord,and quantum condition entropy, while the lower bound consists of the complementarity of the observables and the complementarity of uncertainty.Thus,there exists a relationship between the complementarity of uncertainty and the complementarity of information.In addition, the bounds of the complementarity of uncertainty and the bounds of the quantum discord can exist as essential factors to enhance the bounds of each other.

The paper is organized as follows.Section 2 gives the bounds of the multiple quantum memory-assisted entropic information exclusive principle for multiple measurements and the bounds of the tripartite quantum memory-assisted entropic information exclusive principle for multiple measurements,and in Section 3,the application is given to examine the lower and upper bounds.Finally,the conclusion is drawn.

2.The multiple quantum memory assisted information exclusion principle for multiple measurements

Firstly, we briefly describe an information gain game amongN+1 participants,Alice(A),and herNfriends(Bi,i ∈D:={1,2,...,N}).Suppose that Alice’s friends prepare a composite quantum stateρAB1B2...BNin?N+1d-dimensional Hilbert space and then send the particleAto Alice.Alice and her friends agree on a group of measurements{Πi},i ∈Dwith|iα〉 denotingαth eigenvector of theΠi.Subsequently, Alice randomly chooses one measurementΠiand performs it on herself.She will obtain the corresponding measurement outcomes.Then,she announces her choice to her friendBi.They try to predict the information gained about Alice’s measurement outcomes.

During the processing of measurement, when Alice puts the measurement{Πi}on herself, it will destroy the quantum correlation between her and her friendBi.The quantum correlation (quantum discord) can be defined as the difference between the total correlation and classical correlation,that is,[47,48]

whereI(A:Bm)=H(ρA)+H(ρBm)-H(ρABm)is the total correlation,andJA(ρABm)is the classical correlation that can be defined as

with the mutual informationI(Ω:Bm)=H(ρΩ)+H(ρBm)-H(ρΩBm)of the post-measurement state

According to these rules of the game, based on the entropic uncertainty relation for multiple measurements,we obtain the multiple quantum memory-assisted information exclusion principle for multiple measurements.

Theorem 1The subsystemAof the composite quantum stateρAB1B2...BNis measured by the set of observables{Πi},i ∈D:={1,2,...,N}.The multiple quantum memoryassisted information exclusion principle for multiple measurements will be restricted by the observables’complementarity,the conditional von Neumann entropy, and the quantum discord.

where the upper bound and lower bound are,respectively,

with??given by Eq.(8).

ProofBased on the definitions of the quantum mutual informationI(A:B)=H(ρA)+H(ρB)-H(ρAB)and the quantum condition entropyH(A|B) =H(ρAB)-H(ρB), one can obtain

Based on the relation (15), the uncertainties of the multiple measurements in the presence of the multiple quantum memory can be expressed as

In the last equality, while we add the quantum mutual informationI(A:Bk)and delete it,the equality holds.

Regrouping the terms yields

Due to the inequalityH(Π)≤log2d,the upper bounds of the information exclusion principleU?holds.

For the lower bounds of the information exclusion principle, we also substitute the relation (15) into the uncertainties of the multiple measurements in the presence of the multiple quantum memory,it will arrive at

Rearranging the relation(18),we have

The proof is finished.

Corollary 1The shareability of quantum discord among different parties of theN+1 composite quantum system can be constrained by the entropic uncertainty relation

For the tripartite pure quantum stateρABCor the tripartite mixed quantum stateρABC=|ψ〉A(chǔ)(BC)L ?|ψ〉A(chǔ)(BC)R, the shareability of quantum discord among different parties can be given by

with ～δ=??+H(X|B)+H(Y|C)-H(A|B)-H(A|C).

ProofThe proof is evident.We rearrange the elements of inequality in Theorem 1,and it will arrive at Eq.(20).For the tripartite pure quantum stateρABCor the tripartite mixed quantum stateρABC=|ψ〉A(chǔ)(BC)L ?|ψ〉A(chǔ)(BC)R,it means that there exist two observablesXandYoperated on the subsystemA,the result will be reduced to

We can obtain

with ～δ=H(X|B)+H(Y|C)-H(A|B)-H(A|C)-??.

Notice that there exists the relationH(ρA)=QA(ρA:BC)for all tripartite pure quantum state|ψ〉A(chǔ)BC.For the mixed quantum stateρABC, there exists a factorizationHBC=H(BC)L ?H(BC)Rin the Hilbert spaceHBC, thus the mixed quantum stateρABC=|ψ〉A(chǔ)(BC)L ?|ψ〉A(chǔ)(BC)R, the relationQA(ρA:BC)=QA(|ψ〉A(chǔ)(BC)L)=H(ρA)holds.[49]It will arrive at the relation(21).The proof is completed.

It is worth noting that, from this relation, one can find that the sum of the quantum discordQA(ρAB) andQA(ρAC)of the tripartite quantum stateρABCwill be restricted by theQA(ρA:BC) and the parameter ～δwhich contains the uncertainties of the measurementsXandYand the incompatibility of the measurements??excluding the effects of quantum entanglementH(A|B) andH(A|C).However, in Ref.[50],the shareability of quantum discord among different parties of a composite system is given byQA(ρAB)+QA(ρAC)≤

δ+QA(ρA:BC)withδ=??+H(X|B)+H(Y|C)-H(A|B).It is evident that ～δ ≤δ,thus the bound of Corollary 2 is tighter than the result of Ref.[50].Notably,the shareability of quantum discord among different parties of the tripartite quantum system is consistent with the recent results in Ref.[51].

Corollary 2The relation between the complementarity of uncertainty and the complementarity of information

ProofThe proof is evident.We rearrange the elements of inequality in Theorem 1,and it will arrive at Eq.(24).

Next, we derive the tripartite quantum memory-assisted information exclusion principle for multiple measurements.For tripartite quantum systemρABC, the multiple measurementsNcan be randomly divided into two partsNBandNC,which satisfyNB+NC=N.Suppose thatNBmeasurements are performed on subsystemA, Alice tells her choice to Bob,B.In contrast,NCmeasurements are performed on subsystemA; Alice announces her choice to Charlie,C.Subsequently,Bob and Charlie try to quantify the information gained from Alice’s measurement outcomes.There exists the following information exclusion principle.

Theorem 2For any tripartite quantum stateρABCmeasured by the set of observables{Πi,i=1,2,...,N},the quantum memory-assisted information exclusion principle for multiple measurements will be given by

where the lower and upper bounds are,respectively,

with(Ξ, ～Ξ)standing for(B,C)or(C,B).It is equivalent to

ProofFor the lower bounds of the tripartite quantum memory-assisted information exclusion principle for multiple measurements, we substitute the relation (15) into the uncertainties of the multiple measurements in the presence of the multiple quantum memory,it will arrive at

where(Ξ, ～Ξ)stands for(B,C)or(C,B).Rearranging the relation(27),we have

For the upper bounds of the tripartite quantum memory assisted information exclusion principle for multiple measurements, we start from the uncertainties of the multiple measurements in the presence of the tripartite quantum memory in terms of relation(15),

Regrouping the terms yields

The proof is completed.

One will find this lower bound is similar to the result in Theorem 1; that is, the incompatibility of the measurements??,the quantum discord between the measured subsystem and each unmeasured subsystem,and the conditional quantum entropy in the lower bound also exist.It is evident that the quantum measurements performed on subsystemAbring the uncertainties of the measurements while the quantum correlation of the quantum system is destroyed simultaneously.This result could reveal that the information gain corresponding to the measurement can be maximized only at the expense of the information gains corresponding to complementary observables and quantum correlations.In other words,the quantum correlation within the composite quantum system is also restricted by the uncertainties of the measurements.According to this division and combination idea,it can be extended to multiple quantum states that the number of measurements is more than the number of quantum memory-assisted systems.

3.Applications for three projective measurements

As applications, in order to verify the effectiveness of the information exclusion principle, we consider three two-dimensional observablesΠ1=|0〉〈1|+|1〉〈0|,Π2=-i|0〉〈1|+i|1〉〈0|,Π3=|0〉〈0|-|1〉〈1|measured on the generalized W state which is given by

whereθ ∈[0,2π],φ ∈[0,π],andφ ∈[0,π].

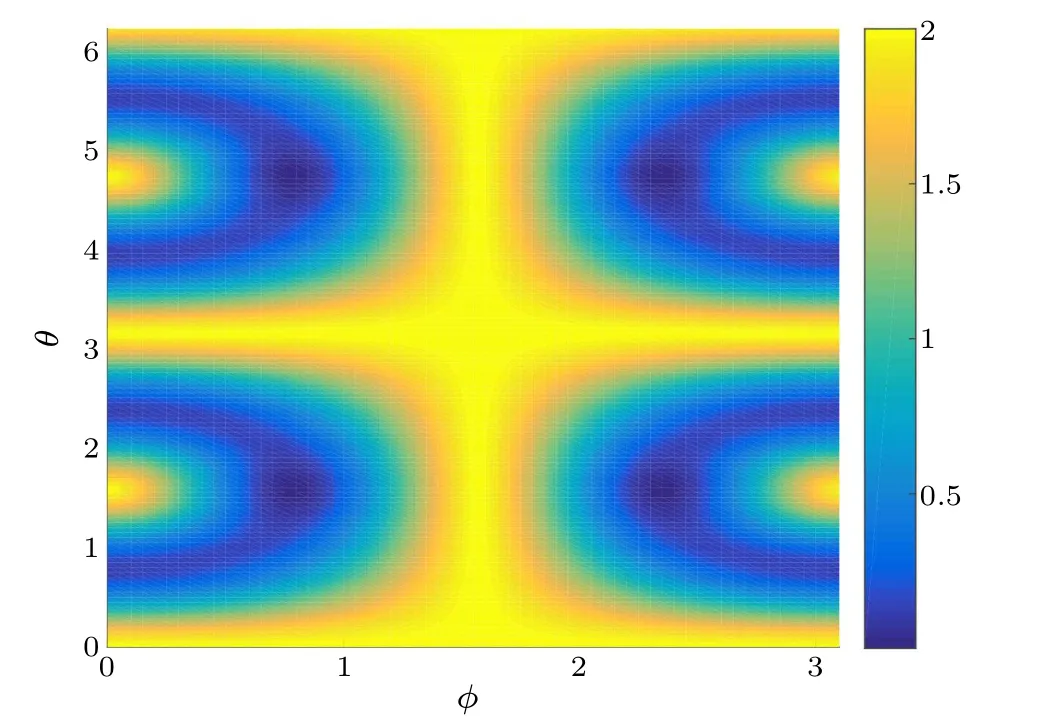
Fig.1.The difference between the upper bound U? and the complementarity of information C?(Π)versus the parameters θ and φ of the quantum state.

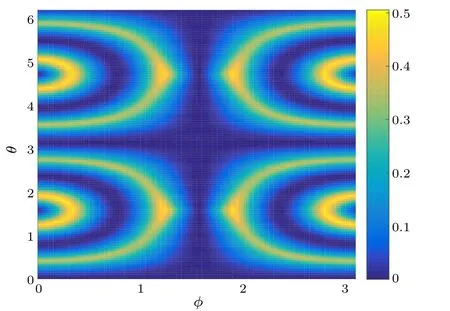
Fig.2.The difference between the complementarity of information C?(Π)and the lower bound L? versus the parameters θ and φ of the quantum state.

Figure 1 shows the difference between the complementarity of information of the three two-dimensional observables and the upper bound given by Theorem 1 versus the parametersθandφof the quantum state withφ=π/3.Figure 2 similarly shows the difference between the complementarity of information and the lower bound given by Theorem 1.The differences are always positive with the increasing parametersθandφ.It is illustrated that,for the generalized W state,the information gained from the observables are well bounded by the effective upper and lower bounds.Namely,the information gain corresponding to the selected observablesΠi(i=1,2,3)can be maximized at the expense of the information carried by complementary observables,quantum discord,and the conditional quantum entropy,which are quantities between the observed subsystem and the quantum memory-assisted subsystems.Figure 3 shows the relationship between the complementarity of uncertainty and the complementarity of information versusθfor the quantum state withφ=π/8 andφ=π/3.It indicates that the lower bound depends on the complementarity of the observables and the conditional quantum entropy of subsystemρAand shows that the limitations on our ability to simultaneously predict the measurement outcomes and information gained from non-commuting observables.

Fig.3.The sum of the complementarity of uncertainty CU(Π)and the complementarity of information C?(Π) with the lower bound versus the parameter θ of the quantum state.

4.Conclusion

As the fundamental features of quantum information theory, we mainly consider the multiple quantum memoryassisted information exclusion principle for multiple measurements.The nontrivial upper bound can be determined by the complementary of measurements, quantum discord, and the conditional quantum entropy,which are quantities between the observed subsystem and the quantum memory-assisted subsystems.They describe the effects of quantum correlation(including quantum discord and quantum entanglement) on the information exclusion principle.They imply that the information gain corresponding to any selected observables can be maximized only at the expense of the information gains corresponding to the observables’ complementary and quantum correlations.In addition, there exists a relationship between the complementarity of uncertainty and the complementarity of information which describes the limitations on our ability to simultaneously predict the measurement outcomes and information gained from non-commuting observables in quantum theory.What’s more,the shareability of quantum discord among different parties of the composite quantum system is restricted by the complementarity of uncertainty.As a consequence,the results shed new light on the quantum entropic uncertainty relation, information exclusion principle, and quantum correlation.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.12271394, 11775040,and 12011530014), the Natural Science Foundation of Shanxi Province, China (Grant Nos.201801D221032 and 201801D121016),the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (Grant No.2019L0178), the Key Research and Development Program of Shanxi Province(Grant No.202102010101004),and the China Scholarship Council.