基于機(jī)器學(xué)習(xí)的盾構(gòu)掘進(jìn)地表沉降回歸預(yù)測(cè)模型

方詩圣, 蘇一恒, 林彤彤, 修賢好, 李建豪

(1.合肥工業(yè)大學(xué) 土木與水利工程學(xué)院,安徽 宣城 242000; 2.合肥工業(yè)大學(xué) 計(jì)算機(jī)與信息學(xué)院,安徽 宣城 242000)

城市地鐵盾構(gòu)工程施工引起地表沉降與塌陷問題因其對(duì)城市建筑物及道路的危害性受到工程界廣泛的關(guān)注,大量學(xué)者正在進(jìn)行相關(guān)研究[1-2]。現(xiàn)有的地表沉降預(yù)測(cè)方法可分為經(jīng)驗(yàn)和半經(jīng)驗(yàn)公式[3-4]、解析法[5]、數(shù)值模擬[6]、模型試驗(yàn)[7]、機(jī)器學(xué)習(xí)算法預(yù)測(cè)[8]。

Peck公式是最早建立在隧道掘進(jìn)地表沉降變形觀測(cè)數(shù)據(jù)上的經(jīng)驗(yàn)公式。文獻(xiàn)[3]研究了基于Peck公式的雙線盾構(gòu)引起的土體沉降前后期結(jié)算疊加的三維計(jì)算公式;文獻(xiàn)[4]研究了利用合肥軌道交通盾構(gòu)施工中的地表監(jiān)測(cè)數(shù)據(jù)對(duì)Peck公式進(jìn)行驗(yàn)證,預(yù)測(cè)值與真實(shí)值平均誤差為8%。解析法在假設(shè)條件下建立力場(chǎng)求解。經(jīng)驗(yàn)法簡(jiǎn)單易行準(zhǔn)確性較差,解析法精度較高但依賴于特定條件,兩者不適應(yīng)于復(fù)雜工程地形。數(shù)值模擬通過ANSYS、ABAQUS、FLAC3D等數(shù)值模擬軟件綜合考慮施工條件和土體參數(shù),模擬隧道開挖過程。但前期準(zhǔn)備工作復(fù)雜且預(yù)測(cè)結(jié)果受模型劃分等因素影響較大。模型試驗(yàn)通過幾何比例物理?xiàng)l件相似的裝置簡(jiǎn)化研究地表沉降,不適用于工程生產(chǎn)。

作為近年新興的一類方法,機(jī)器學(xué)習(xí)是使用統(tǒng)計(jì)技術(shù)從觀察到的數(shù)據(jù)中構(gòu)建模型的方法。針對(duì)傳統(tǒng)預(yù)測(cè)方法精度不高或求解困難的問題,本文基于多種機(jī)器學(xué)習(xí)算法的擬合能力,提出盾構(gòu)掘進(jìn)沿線地表最大沉降值預(yù)測(cè)模型并評(píng)價(jià)出最優(yōu)算法。

1 沉降預(yù)測(cè)方法

1.1 模型框架

本文采用機(jī)器學(xué)習(xí)算法搭建模型,用于預(yù)測(cè)盾構(gòu)掘進(jìn)引起的環(huán)線中心線位置地面縱向沉降穩(wěn)定值,盾構(gòu)掘進(jìn)沉降示意圖如圖1所示。

圖1 盾構(gòu)掘進(jìn)沉降示意圖

用于盾構(gòu)掘進(jìn)過程中的沉降預(yù)測(cè)模型框架可分為3個(gè)階段,如圖2所示。

圖2 沉降預(yù)測(cè)模型框架圖

1) 數(shù)據(jù)收集階段。監(jiān)測(cè)地表沉降并繪制地面沉降圖,獲得地表最大沉降值。根據(jù)需要并結(jié)合實(shí)際選取3類特征參數(shù)(可控不可預(yù)測(cè)類、不可控可預(yù)測(cè)類、不可控不可預(yù)測(cè)類)作為數(shù)據(jù)集中的輸入?yún)?shù)。

2) 學(xué)習(xí)階段。將數(shù)據(jù)進(jìn)行預(yù)處理,篩去異常的數(shù)據(jù),保留合理的數(shù)據(jù)。輸入至回歸預(yù)測(cè)模型中,調(diào)整超參數(shù)進(jìn)行訓(xùn)練。對(duì)預(yù)測(cè)值采用均方誤差(mean square error,MSE)、均方根誤差(root mean square error,RMSE)、絕對(duì)均值誤差(mean absolute error,MAE)和決定系數(shù)R24種評(píng)估指標(biāo)進(jìn)行評(píng)價(jià),選取性能最好的模型用于實(shí)際預(yù)測(cè)。

3) 預(yù)測(cè)階段。將之前已經(jīng)選好的數(shù)據(jù)集中的輸入?yún)?shù)代入學(xué)習(xí)階段中性能最好的回歸預(yù)測(cè)模型中,即可得出地表最大沉降預(yù)測(cè)值。將輸出值與實(shí)際值進(jìn)行對(duì)比,分析其可靠程度。

1.2 模型算法

機(jī)器學(xué)習(xí)中與回歸有關(guān)的模型眾多,理論上可以用回歸方法分析地表隧道中心線位置的沉降值與影響因素之間的關(guān)系。本文中用到的回歸模型主要有線性模型、樹模型、支持向量機(jī)(support vector machine,SVM)、多層感知機(jī)(multi-layer perceptron,MLP)。

1.2.1 線性模型

多元線性回歸分析是最基礎(chǔ)的回歸分析方法,其回歸模型如下:

(1)

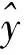
線性回歸模型的損失函數(shù)選擇MSE,計(jì)算公式為:

(2)

其中:m為樣本數(shù)量;wi為模型的系數(shù);xi為樣本自變量;yi為對(duì)應(yīng)的實(shí)際觀測(cè)值。

嶺回歸是一種改良的最小二乘估計(jì)法,通過對(duì)系數(shù)的大小施加懲罰來解決普通線性回歸的一些問題。

(3)

套索算法(least absolute shrinkage and selection operator,LASSO)是另一個(gè)正則化的線性模型,可以降低給定解對(duì)特征數(shù)的依賴程度。它的損失函數(shù)在式(2)添加正則化項(xiàng),即

(4)

1.2.2 樹模型

分裂決策樹(classification and regression tree,CART)[9]構(gòu)建二叉決策樹,遞歸生成CART回歸樹,并通過控制樹的深度來停止分支節(jié)點(diǎn)的分裂。

本文中用到的是隨機(jī)森林的回歸模型,使用了CART回歸樹作為弱學(xué)習(xí)器。使用隨機(jī)森林進(jìn)行地表中心線最大沉降值預(yù)測(cè)的過程如下:首先在訓(xùn)練數(shù)據(jù)集中Bootsrap抽樣(隨機(jī)且有放回抽取),構(gòu)成n個(gè)不同的子樣本;然后在每個(gè)樣本生成1棵CART回歸樹;最后,通過對(duì)構(gòu)建的若干個(gè)不同的CART回歸樹預(yù)測(cè)結(jié)果取平均獲得最終沉降預(yù)測(cè)值如圖3所示。

圖3 隨機(jī)森林預(yù)測(cè)過程

XGBoost(extreme gradient boosting)是一個(gè)優(yōu)化的分布式梯度提升庫,可以快速準(zhǔn)確地解決許多數(shù)據(jù)科學(xué)問題,屬于樹模型一類。

1.2.3 支持向量機(jī)

SVM是用于分類、回歸和異常檢測(cè)的監(jiān)督學(xué)習(xí)方法。本文對(duì)數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理使得經(jīng)過處理的數(shù)據(jù)符合標(biāo)準(zhǔn)正態(tài)分布。

本文采用支持向量回歸(support vector regression,SVR)和LinearSVR 2種支持向量回歸方法進(jìn)行實(shí)驗(yàn)。LinearSVR提供了比SVR更快的實(shí)現(xiàn),但只考慮了線性內(nèi)核,不適用于非線性問題。SVR默認(rèn)使用徑向基函數(shù)。在使用徑向基函數(shù)訓(xùn)練支持向量機(jī)的過程中,重點(diǎn)考慮正則化系數(shù)c和核參數(shù)gamma 2個(gè)超參數(shù)。

1.2.4 多層感知機(jī)

MLP是一種人工神經(jīng)網(wǎng)絡(luò)。在本文中,影響地表中心線最大沉降值的參數(shù)信息通過MLP的輸入節(jié)點(diǎn)流入,中間經(jīng)過2個(gè)隱藏層,神經(jīng)元個(gè)數(shù)分別為20、10,最后經(jīng)過包含1個(gè)神經(jīng)元的輸出層,輸出地表中心線最大沉降預(yù)測(cè)值。其中,隱藏層采用ReLU(rectified linear unit)激活函數(shù),實(shí)現(xiàn)神經(jīng)網(wǎng)絡(luò)層之間的非線性變換,從而提升模型的表達(dá)能力。

1.3 評(píng)價(jià)指標(biāo)

在模型訓(xùn)練中,最終要達(dá)成的目的是得到準(zhǔn)確的預(yù)測(cè),因此尋找真實(shí)值與預(yù)測(cè)值的差異是對(duì)算法模型評(píng)估的關(guān)鍵所在。評(píng)價(jià)預(yù)測(cè)的效果通常需要考慮預(yù)測(cè)的數(shù)值是否正確、擬合程度是否滿意。本文選取以下4種評(píng)估指標(biāo)。

1) MSE的計(jì)算公式為:

(5)

MSE首先計(jì)算每個(gè)樣本的預(yù)測(cè)值與真實(shí)值差值的平方,然后求和再取平均值。MSE的值越小,預(yù)測(cè)模型描述實(shí)驗(yàn)數(shù)據(jù)的精確度越高。

2) RMSE的計(jì)算公式為:

(6)

RMSE也被稱為標(biāo)準(zhǔn)誤差,它是MSE的二次方根。因?yàn)镽MSE與數(shù)據(jù)為相同量級(jí),所以RMSE能更好地描述數(shù)據(jù)。與相當(dāng)于L1范數(shù)的MAE相比,相當(dāng)于L2范數(shù)的RMSE對(duì)異常值更敏感。

3) MAE的計(jì)算公式為:

(7)

MAE為預(yù)測(cè)值與真實(shí)值的誤差絕對(duì)值的均值,能更好地反映預(yù)測(cè)值誤差的實(shí)際情況,其值越小說明擬合效果越好。

4) 決定系數(shù)R2。計(jì)算公式為:

(8)

2 數(shù)據(jù)庫的建立

2.1 數(shù)據(jù)源

數(shù)據(jù)來源于安徽省合肥市軌道交通8號(hào)線北城世紀(jì)城站至泉河路站區(qū)間,位置里程為DK40+670787—DK 42+554836。線路呈V字形坡,最大坡度為25%,線間距13～15 m,埋深9.52～28.07 m;區(qū)間隧道管片內(nèi)徑55 m,外徑62 m,每環(huán)管片寬15 m,平面曲線半徑R≤400 m,曲線段環(huán)寬12 m。所在地貌為二級(jí)階地,巖土層可劃分為3個(gè)單元層和7個(gè)亞層。監(jiān)測(cè)儀器采用TrimbleDINI03,監(jiān)測(cè)點(diǎn)布置為沿線路中心線縱向每10～30 m設(shè)置1個(gè)測(cè)點(diǎn);盾構(gòu)始發(fā)、接收段附近100 m范圍內(nèi),每20 m設(shè)1個(gè)斷面;其余地段,每50 m設(shè)1個(gè)斷面。

2.2 輸入?yún)?shù)

在使用機(jī)器學(xué)習(xí)算法進(jìn)行隧道沉降預(yù)測(cè)時(shí),必須要選取合適的參數(shù)進(jìn)行分析,包括可控不可預(yù)測(cè)、不可控可預(yù)測(cè)、不可控不可預(yù)測(cè)3類。

對(duì)于可控不可預(yù)測(cè)類因素包括所有的盾構(gòu)施工參數(shù)。參數(shù)選取示意圖如圖4所示,在盾構(gòu)施工參數(shù)中,推力、扭矩、貫入度與土倉壓力是盾構(gòu)掘進(jìn)過程中與地層擾動(dòng)有關(guān)的參數(shù),而且它們不但是盾構(gòu)掘進(jìn)控制的重要參數(shù),還可以實(shí)時(shí)獲取、準(zhǔn)確可靠。根據(jù)文獻(xiàn)[10]的研究,注漿量對(duì)盾構(gòu)空隙以及后期的沉降有較大的影響,因此選取這5個(gè)參數(shù)作為輸入?yún)?shù)。

圖4 參數(shù)選取示意圖

對(duì)于不可控可預(yù)測(cè)類因素包括地質(zhì)條件、操作失誤、盾構(gòu)機(jī)缺陷等,在此本文僅考慮地質(zhì)條件。考慮到地質(zhì)條件的復(fù)雜性與隱蔽性,本文僅選取幾個(gè)影響較大的因素作為參數(shù)。文獻(xiàn)[11]在研究中綜合地考慮了巖土層的物理力學(xué)性質(zhì)與空間位置信息,選擇修正標(biāo)貫次數(shù)、修正動(dòng)探次數(shù)、修正單軸抗壓強(qiáng)度這3個(gè)參數(shù)作為輸入?yún)?shù)。文獻(xiàn)[12]研究表明,土體中孔隙水壓力在相對(duì)壓強(qiáng)小于0的范圍內(nèi)降低時(shí),將引起土體等向壓縮,在相對(duì)壓強(qiáng)大于0的范圍內(nèi)降低時(shí),將引起土體單向壓縮,造成沉降。而地下水滲漏會(huì)導(dǎo)致孔隙水壓力降低,因此地下水的深度也作為輸入?yún)?shù)。

對(duì)于不可控不可預(yù)測(cè)類因素包括盾構(gòu)類型、盾構(gòu)埋深與直徑之比、災(zāi)難性地質(zhì)條件3個(gè)因素。對(duì)于同一隧道工程,盾構(gòu)類型未改變,災(zāi)害性地質(zhì)條件難以確定。因此僅考慮盾構(gòu)埋深與直徑之比作為輸入的初始參數(shù)。初始參數(shù)如下:盾構(gòu)總推力為6×104kN;刀盤扭矩為3 100 kN·m;貫入度為36 mm; 實(shí)際土壓力為0.05 MPa; 實(shí)際注漿量為5 m3;修正標(biāo)貫次數(shù)為8.29;修正動(dòng)探次數(shù)為1;修正單軸抗壓強(qiáng)度為50.8 MPa; 地下水的深度為47.109 m; 盾構(gòu)埋深與直徑之比為1.557;監(jiān)測(cè)沉降值為-1.12 mm。3類影響參數(shù)共計(jì)1項(xiàng)內(nèi)容作為初始參數(shù)用于沉降預(yù)測(cè)模型的訓(xùn)練。

3 預(yù)測(cè)結(jié)果

3.1 超參數(shù)確定

超參數(shù)優(yōu)化先確定搜索的參數(shù)空間,然后進(jìn)行抽樣和實(shí)驗(yàn),采用交叉驗(yàn)證的方案來獲得最佳交叉驗(yàn)證分?jǐn)?shù),從而獲得最佳參數(shù)。比如嶺回歸的超參數(shù)α,SVR的核參數(shù)gamma、正則化系統(tǒng)c,隨機(jī)森林的超參數(shù)max-features、n-estimators等等。

嶺回歸的超參數(shù)α表示模型正則化的強(qiáng)度。在模型中,執(zhí)行留一法交叉驗(yàn)證,衡量指標(biāo)默認(rèn)為MSE,α的取值區(qū)間設(shè)置為[0.001,1.001],步長(zhǎng)為0.02。嶺回歸超參數(shù)α與損失值變化如圖5所示,當(dāng)α=0.75時(shí),損失達(dá)到最小值。

圖5 嶺回歸超參數(shù)α與損失值變化

SVR有正則化系數(shù)c和核參數(shù)gamma 2個(gè)重要的超參數(shù)在模型中,SVR的核函數(shù)為徑向基函數(shù)gamma參數(shù)控制單個(gè)訓(xùn)練點(diǎn)的影響距離。嘗試的分布為“c”:uniform(1,10),“gamma”:reciprocal(0.001,0.100)。采樣的參數(shù)設(shè)置數(shù)量n-iters為10,采取隨機(jī)參數(shù)優(yōu)化的方式和三折交叉驗(yàn)證,以R2為衡量指標(biāo),最終確定超參數(shù)c為7.011,gamma為0.026 1。

隨機(jī)森林調(diào)整的超參數(shù)為max-features、n-estimators,max-features為尋找最佳分割時(shí)要考慮的特征數(shù)量,n-estimators為構(gòu)成森林的樹的數(shù)量。本文使用網(wǎng)格搜索(GridSearchCV)進(jìn)行參數(shù)估計(jì)。指定搜索“n-estimators”:[3,10,30],“max-features”:[2,3,4]2個(gè)網(wǎng)格,總共有9種組合。同樣地,采用三折交叉驗(yàn)證,以R2為衡量指標(biāo)。當(dāng)“max-features”: 4,“n-estimators”:30時(shí),交叉驗(yàn)證的評(píng)分最高。

3.2 沉降預(yù)測(cè)結(jié)果

沉降監(jiān)測(cè)值來源于實(shí)地電子激光測(cè)距儀監(jiān)測(cè)。監(jiān)測(cè)值為盾構(gòu)掘進(jìn)到預(yù)設(shè)監(jiān)測(cè)斷面10 d內(nèi)環(huán)線中心處最大沉降值。共收集到358組數(shù)據(jù)。通過噪聲去除,保留270環(huán)真實(shí)可靠數(shù)據(jù)。

從中隨機(jī)選取20%共54組的數(shù)據(jù)作為測(cè)試集,進(jìn)行沉降結(jié)果的預(yù)測(cè)。通過訓(xùn)練集和超參數(shù)確定完善各預(yù)測(cè)模型。將測(cè)試集輸入各預(yù)測(cè)模型,得到盾構(gòu)沉降預(yù)測(cè)值與監(jiān)測(cè)值的結(jié)果,見表1所列。

表1 盾構(gòu)沉降預(yù)測(cè)值與監(jiān)測(cè)值

總體來看,各個(gè)模型總體預(yù)測(cè)值在距離較小時(shí)與實(shí)際值較為符合,其中平均誤差為4%,但部分模型預(yù)測(cè)的最終沉降值與實(shí)際值相差較大,因此需進(jìn)一步對(duì)比分析找出最優(yōu)算法。

3.3 算法性能比較

為進(jìn)一步比較各模型預(yù)測(cè)效果,采用4個(gè)評(píng)價(jià)指標(biāo)比較各算法性能。總體上,神經(jīng)網(wǎng)絡(luò)模型和樹模型擬合效果優(yōu)于線性模型。

對(duì)3個(gè)線性模型性能單獨(dú)分析。線性模型算法性能評(píng)價(jià)結(jié)果如圖6所示。

圖6 線性模型算法性能評(píng)價(jià)結(jié)果

從圖6可以看出,嶺回歸與線性回歸的各個(gè)值都相差不大,嶺回歸的效果會(huì)略好于線性回歸。而LASSO回歸的R2較小,MSE、RMSE和MAE相對(duì)于其他2個(gè)線性模型都偏大,效果最不理想。在對(duì)3個(gè)線性模型分析結(jié)果可知,嶺回歸的效果最好,是線性模型中的最優(yōu)解。

對(duì)樹模型進(jìn)行分析,將隨機(jī)森林與決策樹模型的各個(gè)數(shù)值對(duì)比。樹模型算法性能評(píng)價(jià)結(jié)果如圖7所示。

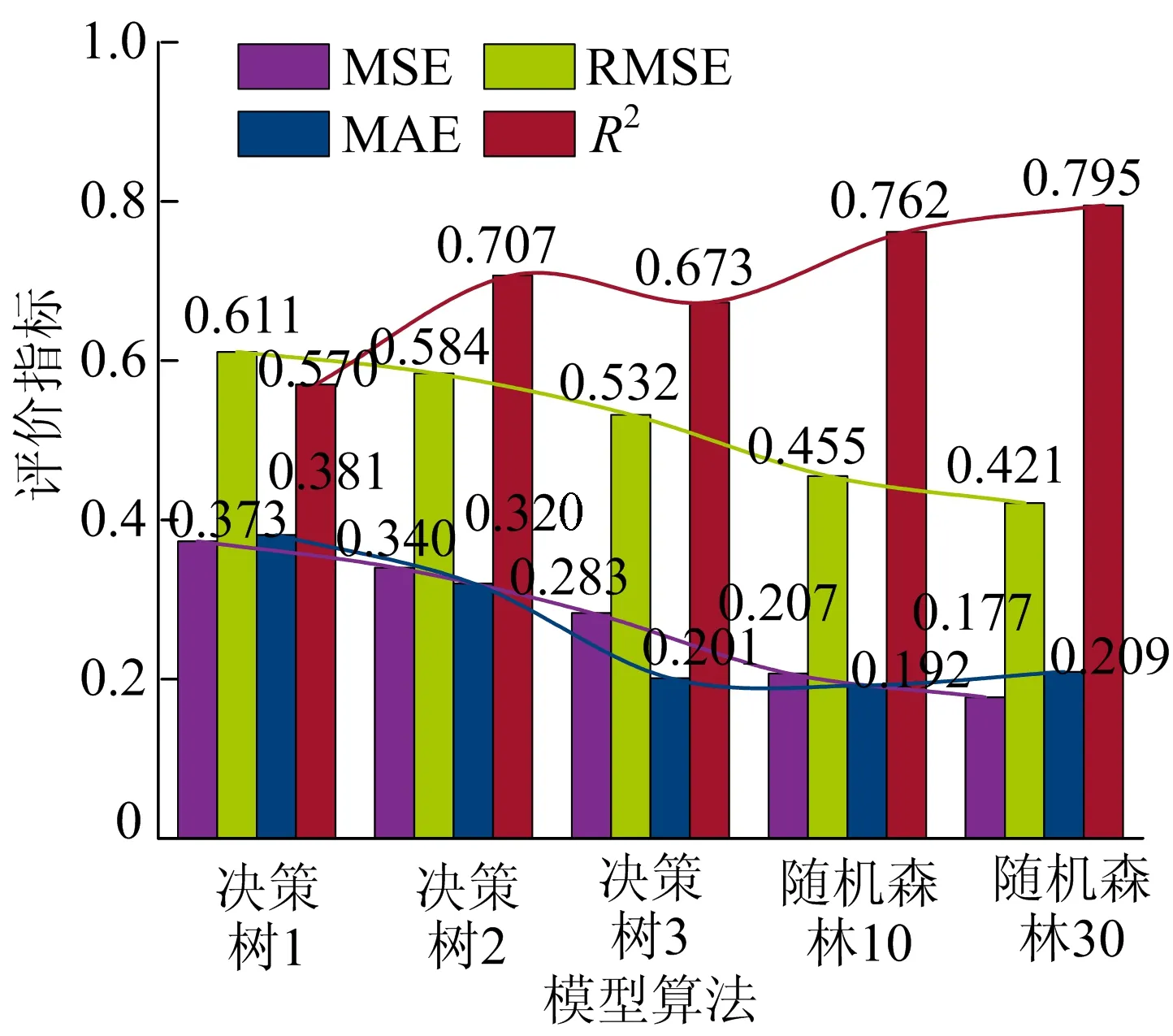
圖7 樹模型算法性能評(píng)價(jià)結(jié)果

圖7中:決策樹1～決策樹3的深度為1～3;隨機(jī)森林10、隨機(jī)森林30的子樣本為10、30。從圖7可以看出,隨機(jī)森林的R2明顯高于決策樹,且隨機(jī)森林的MSE、RMSE和MAE誤差整體都要低于決策樹模型,表現(xiàn)更為穩(wěn)定。在2種樹模型中,隨機(jī)森林的表現(xiàn)效果較優(yōu),可以優(yōu)先選用。

SVR作為SVM的重要分支,其R2顯著高于SVM,且其MSE、RMS和MAE整體都要低于SVM,綜合來看SVR的表現(xiàn)性能要明顯好于SVM的。而MLP的各個(gè)數(shù)值都與SVR相接近,在所有模型中表現(xiàn)性能僅次于SVR。

XGBoost與神經(jīng)網(wǎng)絡(luò)算法評(píng)價(jià)結(jié)果如圖8所示。對(duì)于XGBoost與神經(jīng)網(wǎng)絡(luò)算法,可以優(yōu)先選用SVR作為首選算法,MLP可以作為備選算法來考慮。

圖8 XGBoost與神經(jīng)網(wǎng)絡(luò)算法評(píng)價(jià)結(jié)果

4 結(jié) 論

本文提出了基于多種機(jī)器學(xué)習(xí)算法的盾構(gòu)掘進(jìn)沿線地表最大沉降值預(yù)測(cè)模型,最終通過合肥地鐵軌道8號(hào)線實(shí)測(cè)工程數(shù)據(jù)進(jìn)行評(píng)價(jià)分析確定了最優(yōu)算法。

結(jié)果表明:總體上神經(jīng)網(wǎng)絡(luò)模型和樹模型擬合效果優(yōu)于線性模型;樹模型中隨機(jī)森林與決策樹模型相差微小,隨機(jī)森林表現(xiàn)更為穩(wěn)定;對(duì)于XGBoost與神經(jīng)網(wǎng)絡(luò)算法,SVR的R2顯著高于其余算法,達(dá)到0.865,且其MSE、RMSE和MAE整體較低且較穩(wěn)定,效果最理想。

在處理盾構(gòu)沉降預(yù)測(cè)問題上,SVR算法模型存在對(duì)異常值不敏感,泛化能力強(qiáng),具有較好的魯棒性等優(yōu)點(diǎn)。其預(yù)測(cè)值與真實(shí)值平均誤差率為3.19%,精度較高。

因?yàn)楸疚牡臄?shù)據(jù)庫建立于合肥地鐵軌道8號(hào)線工程,所以不同地區(qū)的土層性能差距較大等客觀因素可能導(dǎo)致沉降值預(yù)測(cè)模型的結(jié)果出現(xiàn)波動(dòng)。