量子近似優化算法在投資組合優化中的應用

吳涵卿，袁淏木，陳柄任，吳 磊，李 鑫，李曉瑜

(1.建信金融科技有限責任公司 上海 浦東區 200120；2.四川元匠科技有限公司 成都 611730；3.電子科技大學信息與軟件工程學院 成都 610054)

近年來，量子計算所獲得的各領域的關注與日俱增[1-2]。然而，容錯(fault-tolerant)量子計算機在近期出現的可能性仍然較低[3]。因此，近期能夠真正付諸實際應用的量子計算算法將主要圍繞中等規模噪聲量子(noisy intermediate-scale quantum,NISQ)計算機展開。大部分NISQ 計算機上的算法都是經典-量子混合的，這類算法將待解決問題中經典計算機上計算較為困難而適合量子計算完成的部分交由量子計算機完成，而其他部分仍然由經典計算機完成。這類算法通過經典計算機上的優化方法，不斷迭代含參量子線路中的參數以得到優化后的量子線路，進而得到所期望的量子態，因而被稱為變分量子算法(variational quantum algorithm, VQA)[4]。

在VQA 中，文獻[5]提出的量子近似優化算法(quantum approximation optimization algorithm,QAOA)能夠高效解決具有特定特征的無向圖上最大割(max-cut)問題。這一問題在經典計算機上是NP 完備的[6]。文獻[7]在其基礎上提出了量子交替算子擬設(quantum alternating operator ansatz,QAOA)，通過對量子線路上算子結構的不同設計，將文獻[5]提出的近似優化算法拓展到有關字符串、排序和流程規劃的一系列問題上，因而可以視作前者的拓展。本文將二者及在其之上進一步衍生的這一類算法統稱為量子近似優化算法，并在下文以QAOA 指代。

目前，除了QAOA 之外，還有運用其他類型的量子算法進行投資組合優化的研究。如文獻[8]提出了基于HHL 的最優化均值-方差模型的方法，這一方法經文獻[9]的拓展，可以解決任意數量的整數約束和預算約束下的均值-方差模型下的投資組合優化問題。文獻[10]提出了NISQ 硬件條件下HHL 解決投資組合優化問題的方法。這些基于HHL 的投資組合優化方案所考慮的解空間是連續的，而非QAOA 所關注的離散化模型。由于HHL 的關鍵要素QRAM 的高效實現仍待探索[11]，因而基于HHL 的投資組合優化算法相較在NISQ時代的實際應用仍有一定的距離。文獻[12]提出了基于Grover 搜索算法的投資組合優化方案，其考慮的問題與下文中介紹的投資組合優化再平衡模型相同，這一方案的優點在于量子線路的設計清晰簡潔，可解釋性強。然而，該算法對于均值向量和協方差矩陣中非整數的系數按比例使用整數近似，受限于NISQ 時代較少的量子比特數，面對非整數參數的投資組合優化問題存在著精度不足的瓶頸。另一方面，利用量子退火進行投資組合優化也是許多研究關注的重點，如文獻[13]對于反向量子退火在投資組合優化中的應用的研究以及文獻[14]對于量子退火中的控制對于無約束組合優化問題求解的影響。量子退火由于其對應的硬件發展較為成熟、規模較大，因此在近期有可能展現量子計算相較經典計算的優勢，但其所能帶來的效率提升如何卻仍待探索[15]。此外，亦有利用量子隨機游走進行投資組合優化的研究[16]，其實際上屬于QAOA 的一種變體。總而言之，QAOA 對于本文所關注的NP 難的離散投資組合優化問題有著精度更高、更可能在NISQ 時代付諸實際應用的優點。

1 均值-方差模型

1.1 馬科維茨的均值-方差模型

均值-方差模型[17-18]是金融學中最經典的模型之一。假設投資者有n個備選資產，其收益率均為隨機變量。這些資產的期望收益率向量為μ=((μ1,)μ2,···,μn)T∈Rn， 收 益 率 的 協 方 差 矩 陣 為Σ=σi j∈Rn×n。 投資者可以對這n個資產進行加權組合。記其在第i個資產上的投資份額為xi，則該投資組 合 的 向 量 表 示 為x=(x1,x2,···,xn)T∈Rn。相 應地，該投資組合的期望收益為 μTx， 方差為xTΣx。投資者希望在給定期望收益 μ0∈R時，最小化投資組合的方差，于是可作如下優化：

由于協方差矩陣一定是半正定的，因此，式(1)可在經典計算機上以多項式時間復雜度的算法解決。

式(1)的一個等價形式如下[19]：

式中， η ∈[0,1]； 1 =(1,1,···,1)T。 η代表了投資者在風險和收益二者間的權衡情況，稱為權衡系數。顯然，當η =0時，投資者只關注收益，傾向于選擇最為激進的投資組合；而當η =1時，投資者只關注方差，傾向于選擇最為穩健、方差最小的投資組合。

1.2 均值-方差模型的離散化

1.3 投資組合再平衡問題

投資組合再平衡(Rebalancing)問題[20]是式(3)的拓展。在再平衡問題中，投資者在決策前已經有一定的持倉y=(y1,y2,···,yn)T。在單筆交易成本T≠0 的 情況下，式(3)相當于y=(0,0,···,0)T的特殊情形，而一般情況下， ?i,yi≠0。于是，就有了本文剩余部分所關注的模型：

顯然，這一問題仍舊是NP 難的。

2 QAOA 的投資組合優化建模

2.1 QAOA 的基本框架

QAOA 將原問題的可變向量映射為量子比特的張量積，經量子線路變換后，將逆映射作用于測量結果得到特定條件下近似最小(大)化目標函數的可變向量取值。以最小化問題為例，QAOA 的基本框架如下。

1)設投資者需要最小化的目標函數為可變向量z的函數f(z),z∈Rn。則需要構造合適的映射φ(·)，φ(z)=|φ〉,〈φ|φ〉=1， 并確定目標函數對應的哈密頓量C，使得f(z)=〈φ|C|φ〉。

4)通過經典計算機上的優化算法(如梯度下降法)，不斷迭代更新參數 γ ,β。每次迭代計算得到新的 γ ,β值之后，重復步驟3)，將新參數下的演化算子作用于初態 |φ0〉，測量末態并計算出新的函數值，進而利用新的函數值算出下一步迭代的 γ,β，直至算法收斂為止。此時，算法得到最終的一組參數γ*,β*及其對應的演化算子U(γ*,β*)。

2.2 投資組合優化問題的QAOA 建模

為形式統一，可以變換式(4)中的交易成本項，得到：

則最小化式(4)中的f(z)等價于最小化：

對于任意zi,i∈{1,2,···,n}， 將其映射到si1,si2兩個量子比特的張量積 |si1〉?|si2〉 上 ，即φ(zi)=|si1〉?|si2〉。令：

具體地，zi和si1,si2的映射關系如表1 所示[20]。

表1 zi 和 si1,si2的映射關系

此外，本文約定φ-1(|1〉?|1〉)=0。

考慮泡利-Z 矩陣(Pauli-Z matrix)：

那么由于：

有關系式zi=〈φ|Ci|φ〉。 因此，目標函數g(z)對應的哈密頓量為：

自此，本文構造完成了上一節步驟1)所需的對應關系，得以進行QAOA 的后續步驟。

3 利用QAOA 進行投資組合優化的不同方法

3.1 軟約束下的標準QAOA

文獻[5]提出QAOA 時所選定的初態為均勻疊

文獻[20]的實驗結果顯示，軟約束下的標準近似優化算法解決投資組合優化問題的效果相較經典窮舉法(brute-force search)沒有明顯的優勢，因此本文的數值模擬將不涉及該方法。

3.2 軟約束下的熱啟動QAOA

對于最大割等整數優化問題，在經典計算機上，可以采用隨機取整(randomized rounding)[23-24]的方法，利用放松原問題的整數約束進行優化所得到的結果尋找整數約束下的最優解。相應地，也可以利用放松整數約束的經典優化結果設計QAOA初態，這種方法被稱作熱啟動[25](warm-starting)。對于式(4)，記：

令：

則s1,s2∈[0,1]n，z=s1-s2。求解：

則軟約束下熱啟動的初態：

相應地，算法使用混合算子U(BSWS,βk)，其中：

當 si=1或 si=0 時 ，BWS僅能在相位的意義上改變相應的量子比特。為了避免出現諸如放松整數約束時的最優解和原問題恰好分別為0 和1 的情形，令：

混合算子U(BSWS,βk)并不能保證優化過程在HD下進行，因此本節引入3.1 節所述的懲罰項A(1Tz-D)2對優化過程進行約束。因此，本文稱本方法為軟約束下的熱啟動QAOA，在下文用SWSQAOA 指代。

3.3 軟約束下的連接熱啟動QAOA

3.2 節中的混合算子U(BSWS,βk)均由單比特門構成，并沒有考慮不同量子比特之間的相關性。因此，一個自然的想法便是在混合算子中引入不同量子比特的相互作用因素。可以構建連接混合算子U(Bcop,βk)[26]，其中：

本文約定n+1 ≡1,n+2 ≡2。是有關參數t∈[-1,1]的 量子門操作，其中t代表不同量子比特之間的相關性，同 γ ,β相同，由經典優化算法確定最優值。自此，本文得到了軟約束下使用連接混合算子的熱啟動QAOA，在下文用SX-QAOA 指代。

3.4 硬約束下的標準QAOA

另一種解決使用X-混合算子時容易得到非可行解的方法是修改混合算子的設計。XY-混合算子[22]U(BXY,βk)能 夠使得只要初態| φ0〉∈HD，近似優化算法一定在 HD內進行，因而能夠顯著地減小算法最小化目標函數的搜索范圍。

在兩類主要的XY-混合算子中，全連接(complete-graph)XY-混合算子[22]考慮了所有可互相交換(即交換后，量子態所對應的資產組合不違背約束條件)的兩個量子比特，在投資組合優化問題的背景下，即：

而環形XY-混合算子(ring mixer)[20,22]僅考慮了相鄰的可互相交換的兩個量子比特。盡管前者在實現效率上較后者略低，但由于其優化效果更好[22]，因此本文選用完全圖XY-混合算子作為硬約束下的混合算子。

4 數值模擬及分析

4.1 數據及參數介紹

本文基于股票收益率和協方差數據進行數值模擬，比較不同QAOA 方法求解投資組合優化式(4)的效果。模擬所使用數據為由2021 年第3 季度A 股3 847 支股票(已剔除單日收益率大于20%及含有缺失值的股票)日收盤價計算得到的日均收益率及收益率協方差數據。

對于p=1,2,3,4的不同情形，本文分別進行1 000次數值模擬。每次數值模擬，均從3 847 支股票中隨機抽取12 支股票，將其日均收益率及收益率協方差矩陣代入式(4)，并分別用經典窮舉法、SWSQAOA、 SX-QAOA 及H-QAOA 進行求解。如圖1所示，在參數設置方面，本文根據一定的分布隨機生成參數y, λ,D的 值。記第m∈Z+次模擬中，參數y, λ,D的 取 值 分 別 為ym=(ym1,ym2,···,ym12)T，λm,Dm，則：

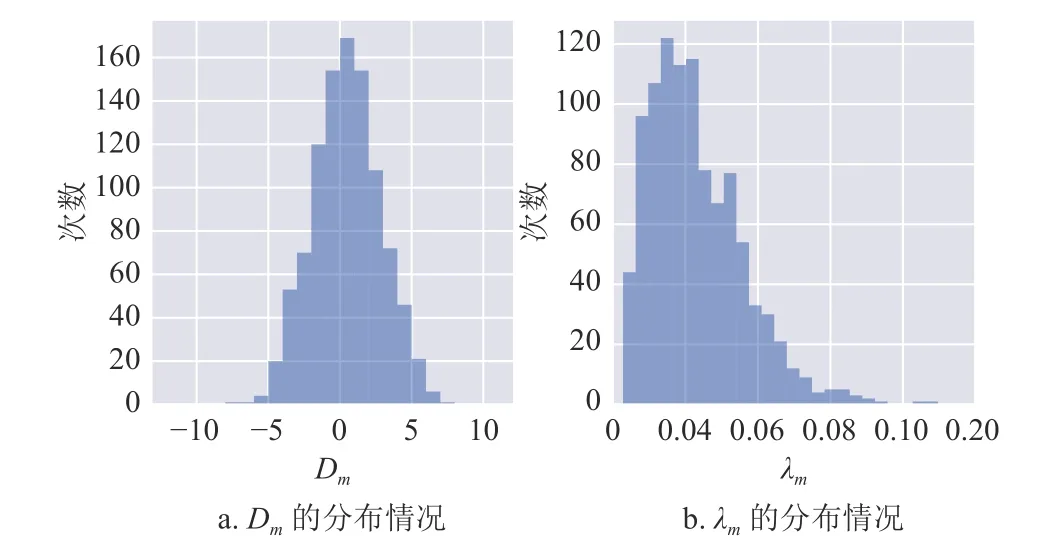
圖1 D m 和 λm的分布情況

此外，本文令 γ,β 的初值均為p維 0 向量，t的初值為0.2，并設置m1=m2=1000, ?=0.25[25]，懲罰項A=50， 交易成本T=0.14。

4.2 數值模擬結果分析

本文從近似比(AR)和成功比例(SR)兩個角度比較不同QAOA 方法的效果。對于第m次實驗，某QAOA 方法的近似比A Rm的定義為：

其中：

而在1 000 次實驗中，某QAOA 方法成功比例 SR的定義為：

即該QAOA 方法成功找到全局最優解的次數比例。

數值模擬的近似比情況如圖2 所示，不同近似比結果的累計密度如圖3 所示。

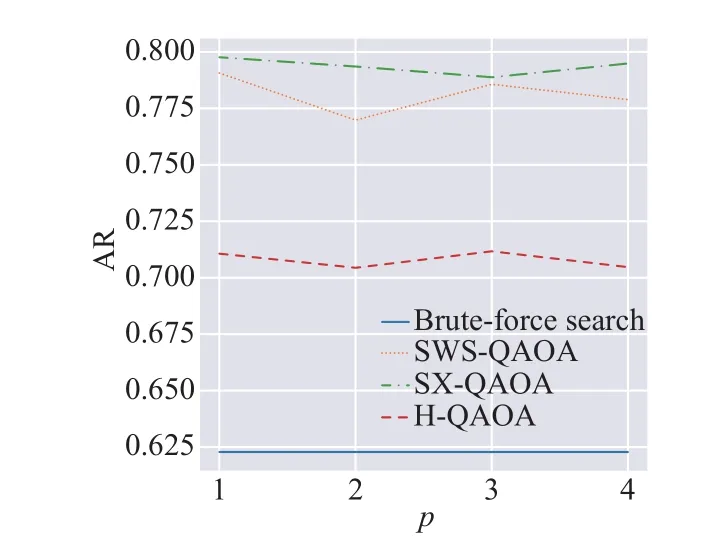
圖2 各方法的平均近似比

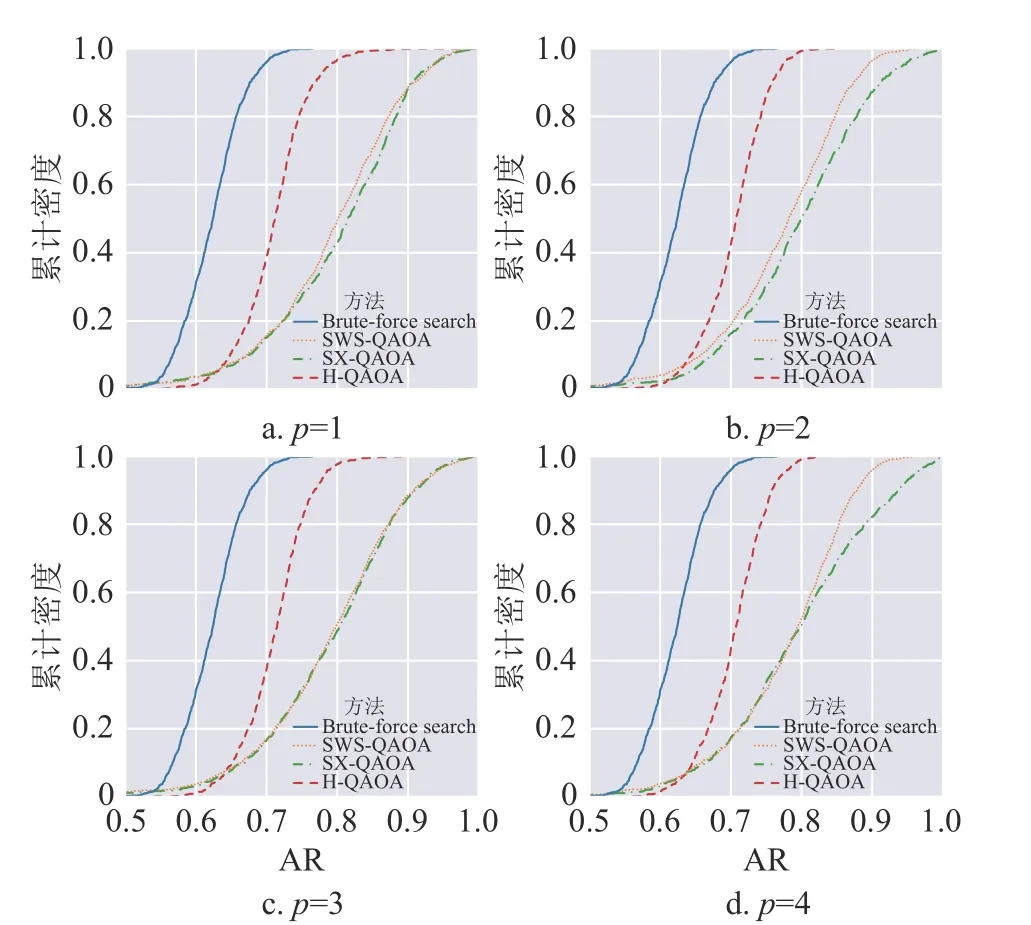
圖3 各方法的近似比的分布

圖中所涉及4 種方法按近似比從高到低排序分別為SX-QAOA、SWS-QAOA、H-QAQA 及窮舉法，各量子算法較經典窮舉法均有至少7%的提升。為了進一步確定不同方法的效果是否有顯著差異，本文基于中心極限定理(central limit theorem)[27]，假定4 種方法近似比的均值均服從正態分布，對其差異進行雙邊t檢驗。本文取上、下臨界值分別為相應t分布的97.5%分位數和2.5%分位數。假設檢驗結果如圖4 所示，可以認為t統計量高于上臨界值說明該組前一方法的平均近似比顯著高于后一方法，若低于臨界值說明該組前一方法的平均近似比顯著低于后一方法。其他情況意味著該組的兩種方法的平均近似比差異不顯著。

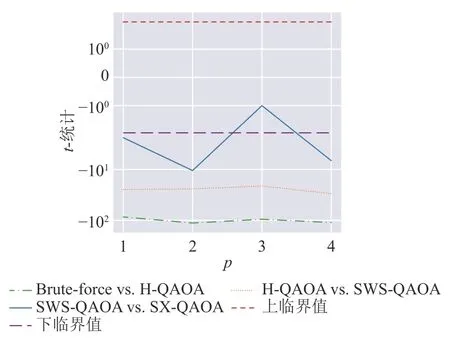
圖4 各方法平均近似比差異的假設檢驗結果

可見，除p=3時SWS-QAOA 和SX-QAOA 的平均近似比差異不顯著之外，其余11 組假設檢驗結果均顯著。本文進一步確定了在近似比的意義上各方法均存在顯著差異。量子算法相較經典窮舉法在平均近似比上均有著顯著的提升，其中SX-QAOA表現最優。

3 種不同QAOA 方法的成功比例情況如圖5 所示。

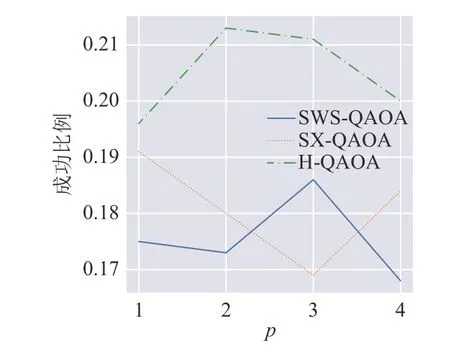
圖5 各方法的成功比例

直觀上看，若將3 種QAOA 方法按照成功比例從高到低排序，則最高的為H-QAOA，但SWSQAOA 和SX-QAOA 較難區分高低。與之前類似，本文進行各方法成功比例差異的雙邊t檢驗，以判斷其是否顯著。結果如圖6 所示。

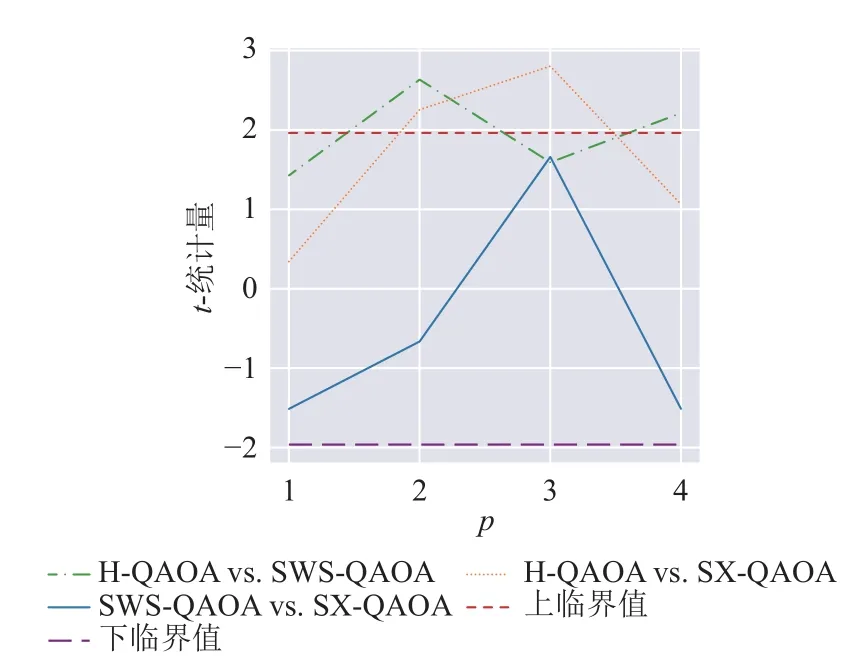
圖6 各方法成功比例差異的假設檢驗結果

可見，僅在p=2及p=4時，H-QAOA 的成功比例顯著高于SWS-QAOA 的成功比例；在p=2及p=3時，H-QAOA 的成功比例顯著高于SX-QAOA的成功比例。而其余組假設檢驗的結果均不顯著。因此，本文認為，在成功比例的意義上，H-QAOA略優于SWS-QAOA 和SX-QAOA，但后二者之間難分伯仲。

5 結 束 語

本文對于QAOA 在投資組合優化中的應用從理論建模、不同方法及數值模擬等多角度進行了詳細的討論。針對未來相關領域的研究，本文有如下兩點展望。

1)回顧前面介紹的各種利用QAOA 進行投資組合優化的方法，可以注意到，軟約束QAOA 能夠利用放松整數約束的經典優化結果進行熱啟動，起到類似經典算法中隨機取整的效果。然而，軟約束QAOA 搜索空間是全狀態空間，而滿足約束條件的子空間 HD僅僅是其中的一個超平面。隨著n的增大，軟約束QAOA 所搜索的空間將幾乎全是非可行的冗余狀態。因此，在測量次數m1,m2不變的情況下，隨著n的增大，軟約束QAOA 很可能將逐漸失效。另一方面，現有的硬約束QAOA 盡管將搜索空間縮小至 HD內，但是并未利用經典優化的結果進行初態設計，存在進一步提升的可能。如何將放松約束的經典優化結果與硬約束的QAOA結合起來將成為一項有價值的課題。

2)從數值模擬結果來看，各QAOA 方法的近似比和成功比例并未隨著p的增大而單調遞增，這表明更加復雜的模型并沒有帶來更好的表現。此外，各QAOA 方法的成功比例均為20%左右，搜索得到全局最優解的概率并不高。導致QAOA 表現不及預期的原因很可能是QAOA 的經典優化過程中常見的所謂貧瘠高原(barren plateau)問題[4,28]以及QAOA 本身存在的可及性缺陷(reachability deficits)問題[29]。前者往往使得經典優化算法提前終止，進而導致QAOA 無法找到理論最優值 |φ*〉；而后者表明，即便找到了 |φ*〉，但可及性缺陷仍然可能較大，這意味著使用某些演化算子的QAOA的效果可能存在著無法逾越的理論上限。如何針對投資組合優化問題設計更加合適的演化算子以解決這些問題亦將是一項富有意義的工作。