皇冠梨靜壓力學特性及模擬研究

吳映桐，吳子鳴，張立軍，孫一鳴，王立軍,2，宋海燕,2*

農產品保鮮與食品包裝

皇冠梨靜壓力學特性及模擬研究

吳映桐1，吳子鳴1，張立軍1，孫一鳴1，王立軍1,2，宋海燕1,2*

（1.天津科技大學 輕工科學與工程學院，天津 300457； 2.中國輕工業食品包裝材料與技術重點實驗室，天津 300457）

建立皇冠梨生理特性與力學損傷關系模型，實現果實靜壓過程的模擬研究。通過材料松弛試驗和靜態壓縮試驗，研究果實材料力學特性。使用三維掃描方法輔助建立果實有限元模型，并對果實靜載損傷過程進行模擬。使用Maxwell黏彈性材料本構模型，成功模擬了果實流變特性。通過靜壓試驗將所建立的梨果實黏彈性材料模型與傳統彈塑性材料模型進行對比，誤差降低了7%，從而驗證了模擬的準確性。根據von Mises等效應力分布結果進行預測，發現在靜載力為161.21 N時梨果實會出現明顯損傷。以上研究使用2種材料對靜態壓縮試驗進行仿真模擬，進一步驗證了使用數值模擬方法對水果靜力學過程模擬的可靠性。為皇冠梨果實機械化采摘、儲存包裝及加工搬運過程提供了理論依據。

有限元模擬；松弛試驗；本構模型；靜壓試驗；水果損傷

我國梨果實年產量約1 781.5萬t，其中河北地區梨果產量的占比超過全國總產量的60%[1]。皇冠梨作為當地梨果的代表，具有極高的營養價值和較好的風味口感。水果等農產品從果園到消費者手中會經歷采摘、包裝、搬運、儲存等過程。在這些過程中，水果很容易受到壓縮力，如機械手采摘時發生夾損、在包裝盒內與其他水果接觸、箱內堆碼時受到擠壓和儲存過程中發生的蠕變行為等[2]。靜壓力會導致包裝內水果發生損傷，細胞壁膜破裂，水果發生軟化，細菌和真菌更容易滲透到受損組織中，導致水果發生褐變從而加速腐爛[3-4]。因此，分析果實承受的壓縮載荷極限，對避免果實在運輸包裝過程中發生機械損傷具有重要意義。

許多學者對番茄、西柚、桃子、梨、蘋果、獼猴桃、西瓜等水果在收獲、儲運過程中的靜載、振動和撞擊的機械損傷問題進行了研究[5-10]。由于不同品種水果之間力學特性存在較大差異，試驗往往需要更加嚴格的試驗環境和裝置。有限元法的實用性在于可以用原型模擬代替物理試驗，從而減少試驗次數。隨著計算機建模技術的發展，數值方法目前已被證明可以與實際試驗之間建立可靠聯系，為預測水果采后損傷敏感度提供理論依據[11]。水果材料的生物流變特性以及細胞間果膠質和纖維組織的影響，使得計算外力在果皮下產生的內應力非常困難[12-13]。因此，采用數值模擬的方式，建立水果材料宏觀-微觀多元力學系統模型是本次研究的重難點問題。

1 試驗

1.1 材料與儀器

主要材料：皇冠梨，采摘自河北省趙縣。按質量和外觀進行分類，選擇單果質量大于300 g且無表面損傷的特級果[14]。在采后運輸過程中，質量和體積較大的水果更容易出現機械損傷，因此在包裝中需要特別注意[15]。特級果實不僅作為水果進出口的首選，還可為其他級別的水果在采摘、搬運和貯藏過程中的力學特性提供參考價值。將成熟的皇冠梨果實從果園采摘后運至實驗室恒溫恒濕（溫度為20 ℃、相對濕度為40%），并貯藏24 h進行預處理。

主要儀器：萬能試驗機，RG1-3，深圳瑞格爾儀器有限公司，該設備最大載荷為10 kN，載荷精度為示值的1%（±0.5%）以內，速度精度為示值的0.5%（±0.15%）以內；Archer Thunk 3D掃描儀，北京科訊有限公司。

1.2 材料性能

1.2.1 彈性參數

為了確定梨果實材料參數，根據ASAE標準[16]基于赫茲理論計算表觀彈性模量。在梨的相對對稱位置沿其莖-萼軸切成兩半。其中一半被置于固定板的中心，選取10個試樣，用萬能試驗機進行壓縮試驗，載荷為1 kN。試驗過程如圖1所示。用曲率半徑儀測量梨與上盤接觸的最大和最小曲率半徑值，并將結果代入式（1）計算彈性模量。

式中：為表觀彈性模量，Pa；為施加在樣品上的壓縮力，N；為壓縮變形，m；為泊松比（無量綱）；U和RU分別為接觸點處表面曲率的最小和最大半徑，m；U為上凸表面的常數。

1.2.2 果皮參數

梨果實多尺度有限元模型的建立還需要對果皮組織的力學特性進行測量。為了分析皇冠梨果皮軸向和徑向力學性能的差異，將果皮分別制成寬為10 mm、長為45 mm、厚為0.5 mm的長方形薄片，軸切向和徑切向的拉伸試樣共20個。使用萬能試驗機進行拉伸試驗，加載速度設定為5 mm/min，記錄下相應的力-位移曲線數據。

圖1 皇冠梨彈性參數測定

1.2.3 黏彈性參數

為了表征梨果實的黏彈性流變特性，本研究參照ASTM標準采用應力松弛試驗方法[17]。由于梨果實各部位的流變學特性、營養供應、光照方位等因素可能對果實石細胞分布產生影響，導致力學特性差異[18]。因此，隨機挑選10個皇冠梨果實，分別在每個果實的上部、中部、軸向和徑向位置取樣進行比較。用直徑為10 mm的軟木鉆提取果肉制成高度10 mm的圓柱體，采樣過程如圖2所示。通過單軸壓縮試驗，以0.1 mm/s的變形速率對試件施加0.05的應變，保持應變值不變，記錄應力與時間的關系[19]。

1.3 靜態壓縮試驗

整果靜態壓縮試驗，可以模擬箱內靜載和采摘過程機械手夾損的情況。通過壓縮試驗機，將皇冠梨放置在2塊堅硬的鋼板之間。壓縮速率為5 mm/min，壓縮位移直至梨果實達到破裂點。具體試驗過程可見圖7中箭頭對應位置。

1.4 三維建模

現實中，由于梨果實具有復雜的非對稱形狀，傳統的幾何建模難以精確復原，而通過逆向工程可以準確地提取水果的三維特征。本研究從無損傷的測試樣品中選取一個具有代表性的皇冠梨。使用非接觸式三維掃描儀捕捉旋轉時果實表面的點云特征，構建水果表面曲面片，建立果實實體模型并測量了果實的幾何參數，如圖3所示。

1.5 靜壓有限元模擬

有限元模擬過程分為前處理、求解和后處理3個階段。將建立的皇冠梨果實多尺度三維實體模型導入有限元分析軟件Abaqus中進行設置。其中，果皮部分采用線彈性材料模型，由殼體單元組成，殼體厚度為0.5 mm。果肉部分為各向同性的實體單元。各層結構間通過面對面接觸關系連接為一個整體。有限元模型網格劃分的單元和尺寸是控制仿真質量的重要因素，合適的網格劃分尺寸既能確保模型準確，又能節省計算時間。經過從6 mm到2 mm的多次網格無關化模擬試驗，最終確定3 mm為最佳尺寸。皇冠梨果皮和果肉網格單元分別采用四面體和四邊形。果皮部分使用S4R殼體單元，節點數為2 429個，單元數為2 424個。果肉部分使用C3D10M型四面體單元，節點數為62 705個，單元數為43 520個。具體有限元模型及網格劃分如圖4所示。

圖2 果肉松弛試驗過程

圖3 皇冠梨幾何模型及各部分尺寸

使用有限元模型進行靜態壓縮試驗模擬，將建立好的皇冠梨實體模型放置在剛性約束的上、下兩極板之間。剛性平面的網格單元采用結構六面體，網格尺寸為10 mm。下壓板為完全固定約束，上壓板沿軸方向以5 mm/min的速度向下移動。壓縮位移為15 mm，直至梨果實達到屈服極限。

圖4 皇冠梨靜壓有限元模型

2 結果與分析

2.1 材料模型

根據上述試驗測定的皇冠梨果皮和果肉的力學特性，分別定義了2種材料模型。依據果實的生物學特性，石細胞、果膠物質和薄壁細胞是影響果肉力學特性的主要因素[20]。結合生物材料的力學本構模型特點，彈性模量通常用于描述生物材料的流變行為，在各向位置相差不大，因此可將梨果肉視為各向同性材料。梨果實的彈性力學特性如表1所示。

表1 皇冠梨材料特性

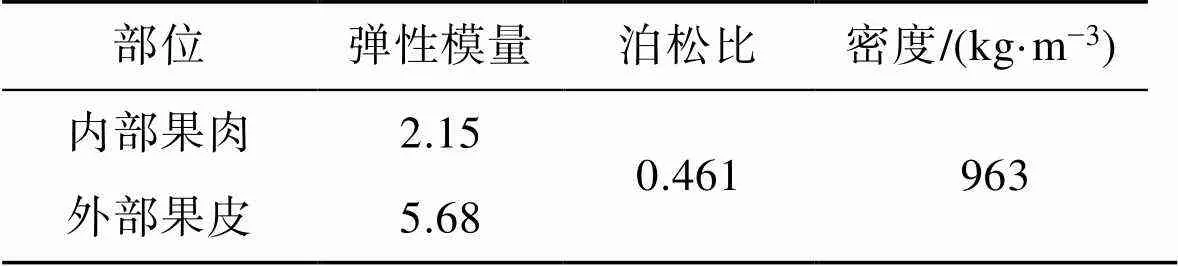
Tab.1 Material characteristics of Huangguan pears

相關文獻表明[21-22]，在水果領域，黏彈性材料可能更接近實際情況。本研究首次建立了皇冠梨果實黏彈性材料本構模型，并將其應用于數值仿真過程。在生物材料中通過模擬模型的黏性元素，來表示線性黏彈性材料的流變行為。將Maxwell模型與力學模型中的2個基本力學要素相結合，反映果實的流變特性。廣義的Maxwell模型表示，使用平衡和衰減模量及松弛時間的Prony系列，用線性彈簧和線黏性減震器來表示水果的黏彈性。2種材料的本構模型關系見圖5。

在Maxwell模型中，所有的初始應力都進入彈簧，導致初始變形階段服從胡克定律。隨著彈簧的變化，壓板承受的應力越來越大，直到應力和應變不能線性變化。最后，所有應力在阻尼器中流動，應力-應變曲線趨于瞬態穩定。在壓縮和應力松弛試驗中，反作用力是由試樣的應變在一段時間內保持恒定得到的[23]。在數值模擬中要對剪切模量和體積模量進行歸一化處理。采用非線性回歸方程對數據進行非線性應力松弛分析。恒應變階段的本構關系可以寫成式（2）～（3）的形式。

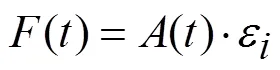
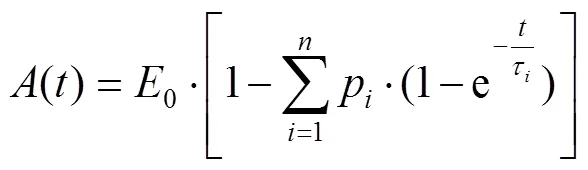
式中：()為松弛函數；p為第階Prony常數（1, 2,）；τ為第階Prony延遲時間常數（=1, 2, …）；0為材料瞬時模量。為了將以上數值帶入數值模擬中，對于線性各向同性彈性系統，假設黏彈性材料由無量綱松弛模量的Prony級數展開定義：

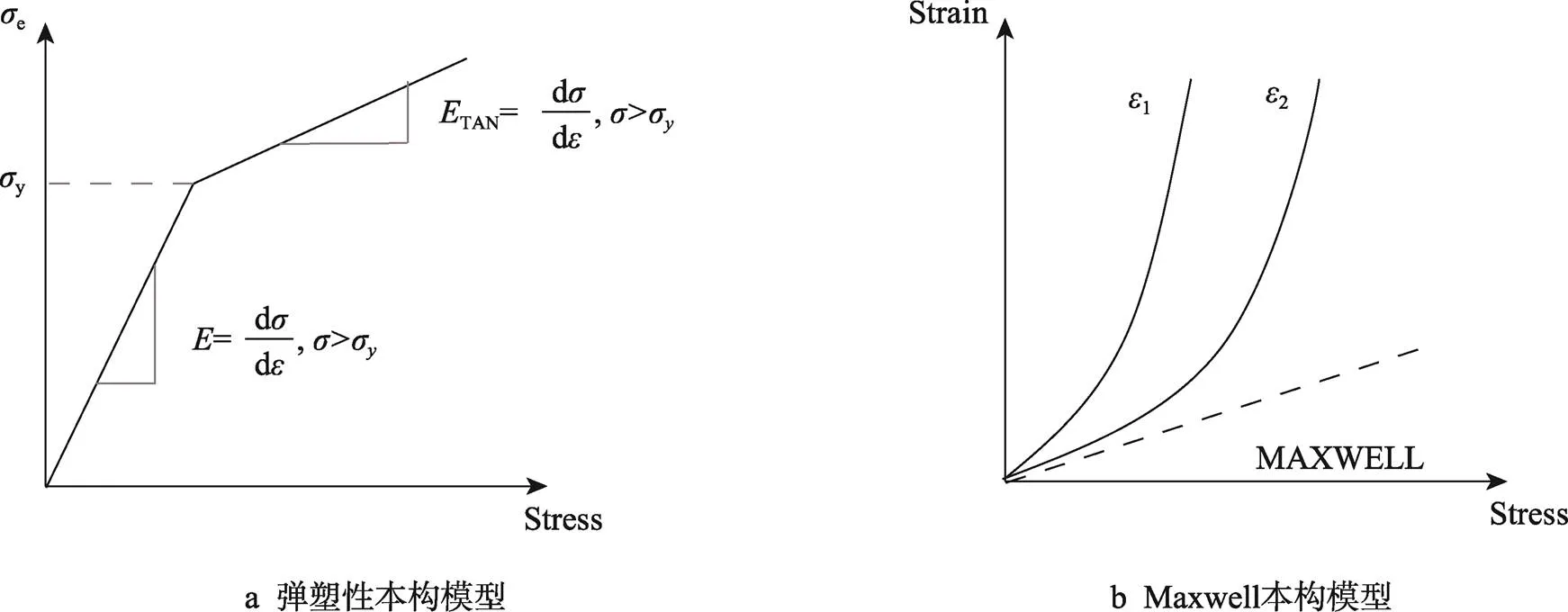
圖5 材料本構模型

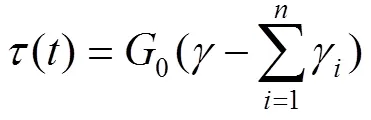
將上述結果作為輸入數據，可以經過推導得出基于廣義Maxwell模型的Prony級數表示法的平衡和衰減模量，以及松弛時間的相關方程[22]，見式（6）～（8）。

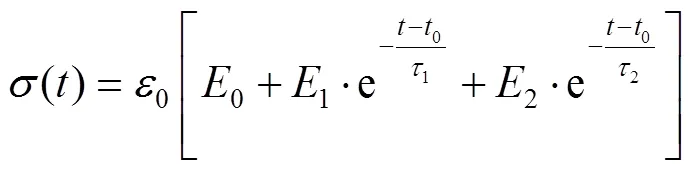
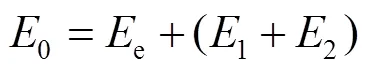
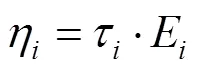
式中：()為松弛應力；0為松弛應變；0為瞬時彈性模量；e為平衡彈性模量；E為衰減彈性模量；τ為Prony級數的松弛時間；η為第項的比黏度。將Prony級數中衰減模量和瞬時模量的商分別對應彈性、剪切和體積模量的分量，見式（9）。

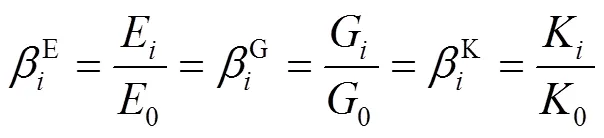
式中：βE、βG和βK分別表示Prony級數第項的彈性模量、剪切模量和體積松弛模量；G和K分別為衰減剪切模量和衰減體積模量的第項。

通過式（9）可以計算出2種比黏度值（1和2）分別為6.54和209.66 MPa?s。對黏彈性材料的時間相關剪切和體積模量進行建模，可以得到數值模擬Prony級數中的值。表2中給出了廣義Maxwell模型非線性模擬結果的參數匯總。

表2 梨果肉Prony系列松弛仿真參數

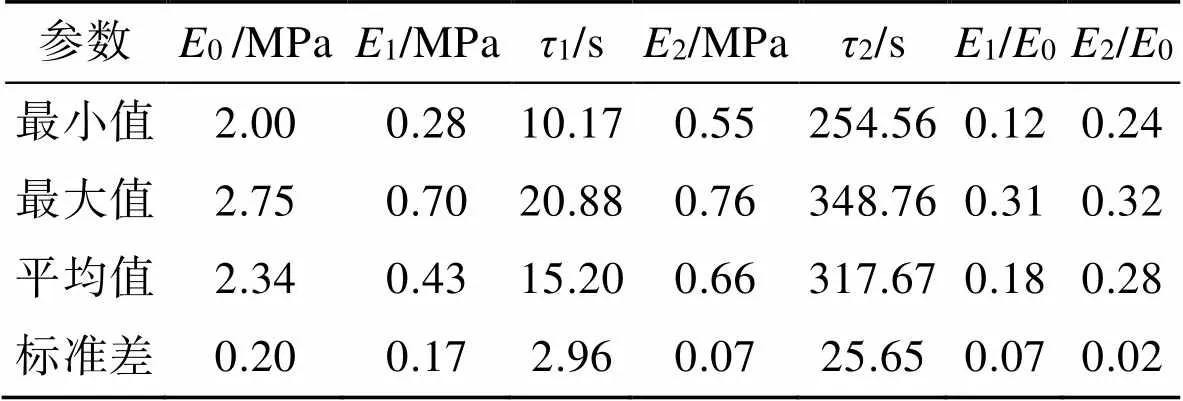
Tab.2 Prony series relaxation simulation parameters of pear flesh

對黏彈性材料模型進行松弛試驗仿真，驗證其力學特性。建立與實體試樣一致的三維圓柱體幾何模型，模擬應力松弛試驗，試驗結果如圖6所示。數值模擬得到的材料力學特性與試驗曲線幾乎一致，面積誤差為1%。證明了使用黏彈性材料表征皇冠梨果實特性的準確性。同時得出，應力為0.3 MPa時，梨果肉細胞組織會發生不可恢復的變形，因此可將此數值作為損傷判定的依據。

2.2 靜壓試驗結果

如圖7所示為10個整果試件在壓縮作用下的力-位移曲線，可以看出梨果實在壓縮位移13～17 mm出現了破裂點。果皮在達到破裂點時突然開裂，大量汁液從內部溢出。這表明梨果實整體在宏觀結構上受到了極大地破壞[23]。同時可以發現，在開裂之前內部果肉可能已經嚴重受損。微觀結構的研究也可以說明，梨果實生物屈服點遠早于破裂點。通過對10組數據進行處理，得到平均力-位移曲線，用于模擬壓縮載荷下全果多尺度的有限元模型。

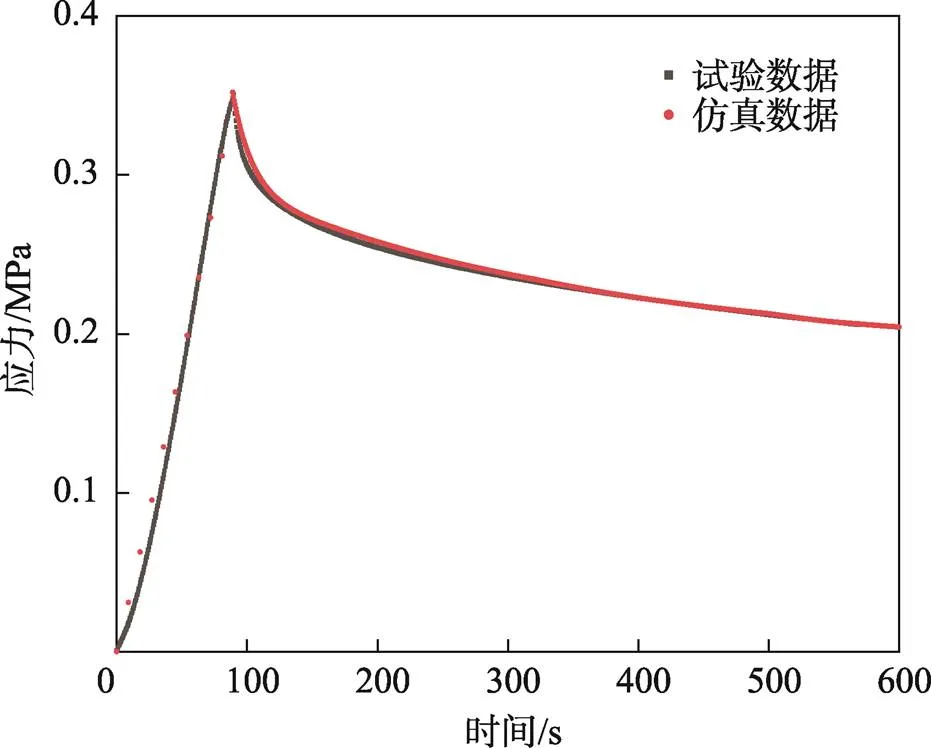
圖6 松弛試驗仿真與試驗對比

圖7 全果靜態壓縮試驗

2.3 靜壓仿真結果

如圖8所示為整個皇冠梨靜態壓縮的有限元模擬過程。由于無法模擬出果皮破裂的過程，因此只對發生失效前的位移進行模擬，共設置180個子步。當壓縮時間達到60子步，位移為4.6 mm時，此時雖然表皮部分未達到應力屈服點，但果肉接觸部分已發生損傷，此時壓縮力為161.21 N。當壓縮位移達到7.4 mm時，果肉出現明顯損傷，此時壓縮力為366.27 N。根據von Mises等效應力分布，此時的應力波從接觸位置傳遞到了果實中心，果實中心部位的果皮和果核承擔了大部分壓縮力。在壓縮位移為15 mm時，中心區域的果肉細胞達到了應力屈服極限，發生了不可恢復的變形，因此等效應力值和變形面積沒有明顯增加。

如圖9顯示了有限元模擬梨果實失效結果與試驗損傷的對比結果，可以看出損傷部分基本吻合，進一步說明了模擬結果的準確性。在模擬過程中，最大等效應力均發生在剛性板與試樣的接觸位置，超過屈服應力強度的區域也主要集中在這個位置，而較小的應力出現在距離接觸較遠的位置。

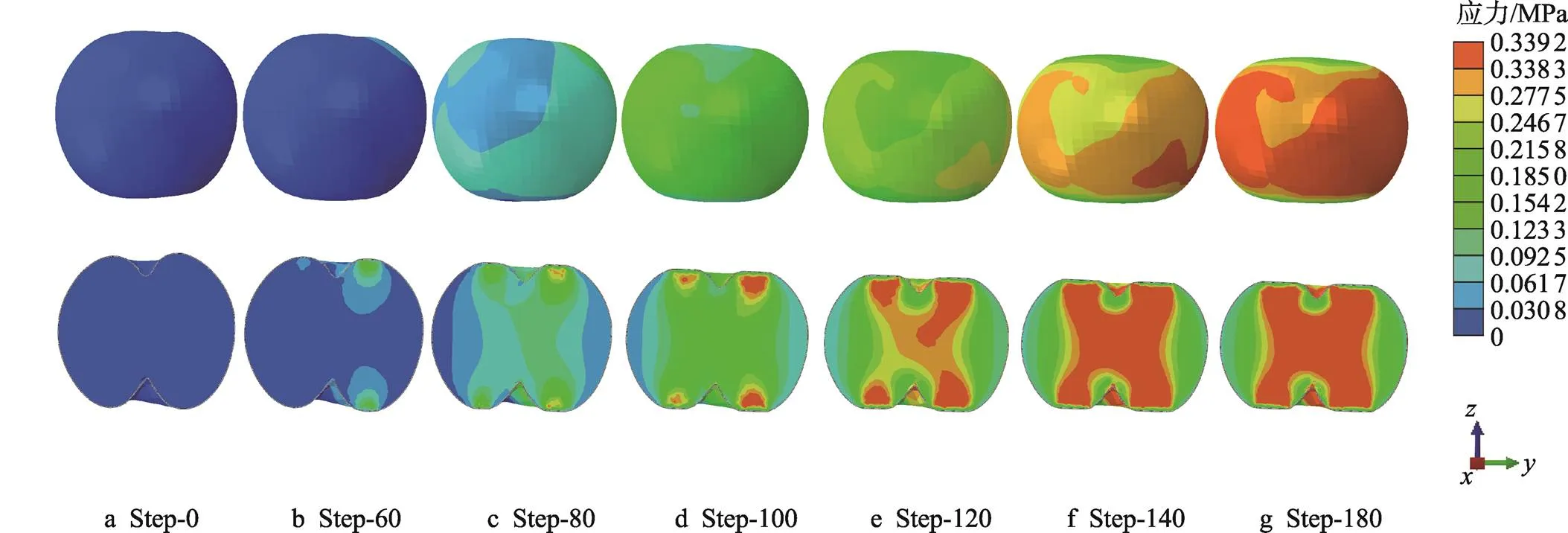
圖8 梨果實靜壓仿真過程及von Mises等效應力云圖

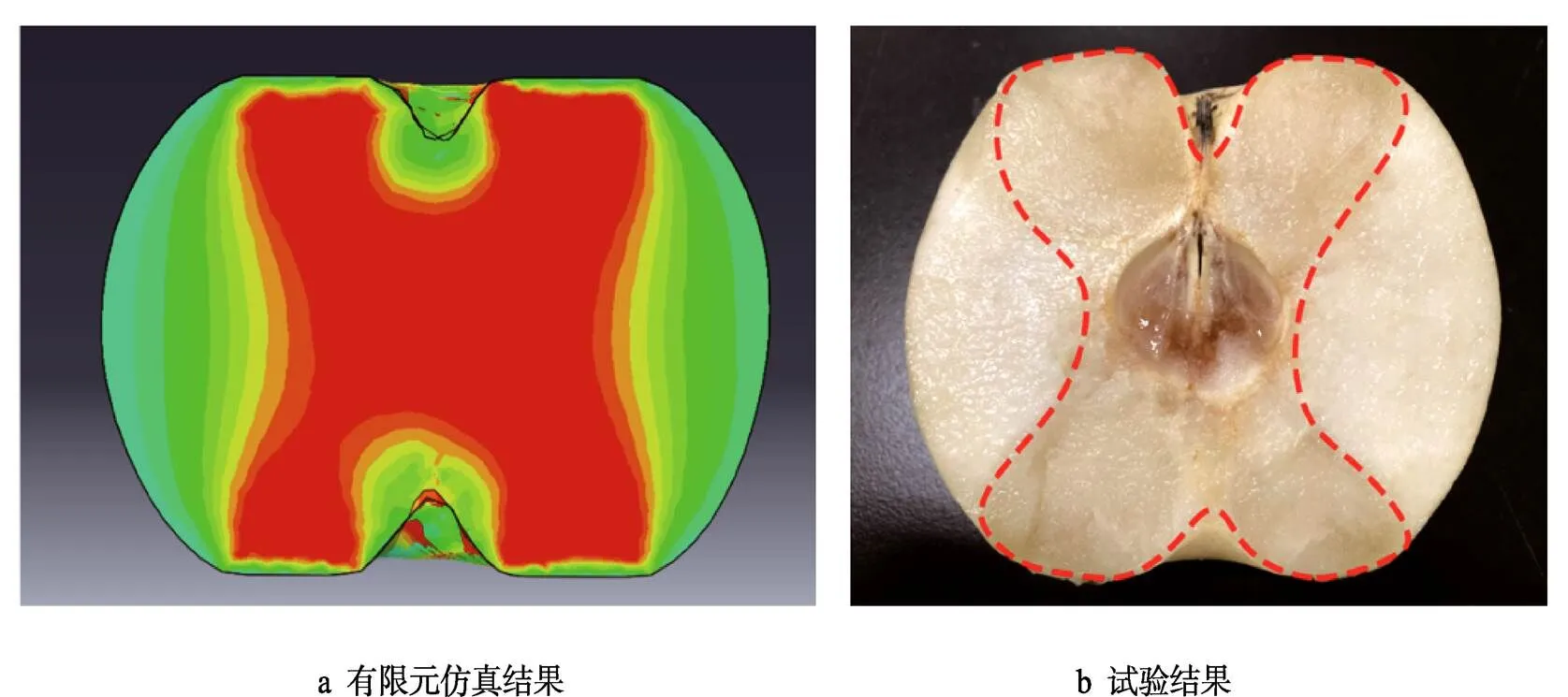
圖9 皇冠梨靜壓損傷對比

2.4 仿真精度分析

從圖10可以得到整個梨的平均失效力和失效位移值分別為（1 098±200）N和（15±2）mm。圖11展示了2種材料的擬合誤差，從數值上看，黏彈性材料與彈塑性材料殘差平方和（RSS）的擬合度分別為4 812和47 916，相對誤差增大了89.95%。峰值點處壓縮力數值分別為1 054 N和970 N，與試驗數據的誤差分別為4%和11%。使用黏彈性材料進行仿真，誤差較小，相對精度提高了7%。果實中存在的果膠、纖維素、水分等物質具有明顯的黏性特征，會影響果實損傷變形時能量的吸收，從而出現延遲性損傷。因此，黏彈性材料在靜態試驗中能更好地表征水果的生理性能。

根據上述研究結果，提出了皇冠梨水果搬運和堆放的建議。為避免徑向壓縮力對果實造成損傷，垂直疊放的水果一次不應超過40層，靜壓力不應超過161.21 N，否則就會造成不可恢復的永久性損傷。

圖10 靜壓仿真與試驗對比

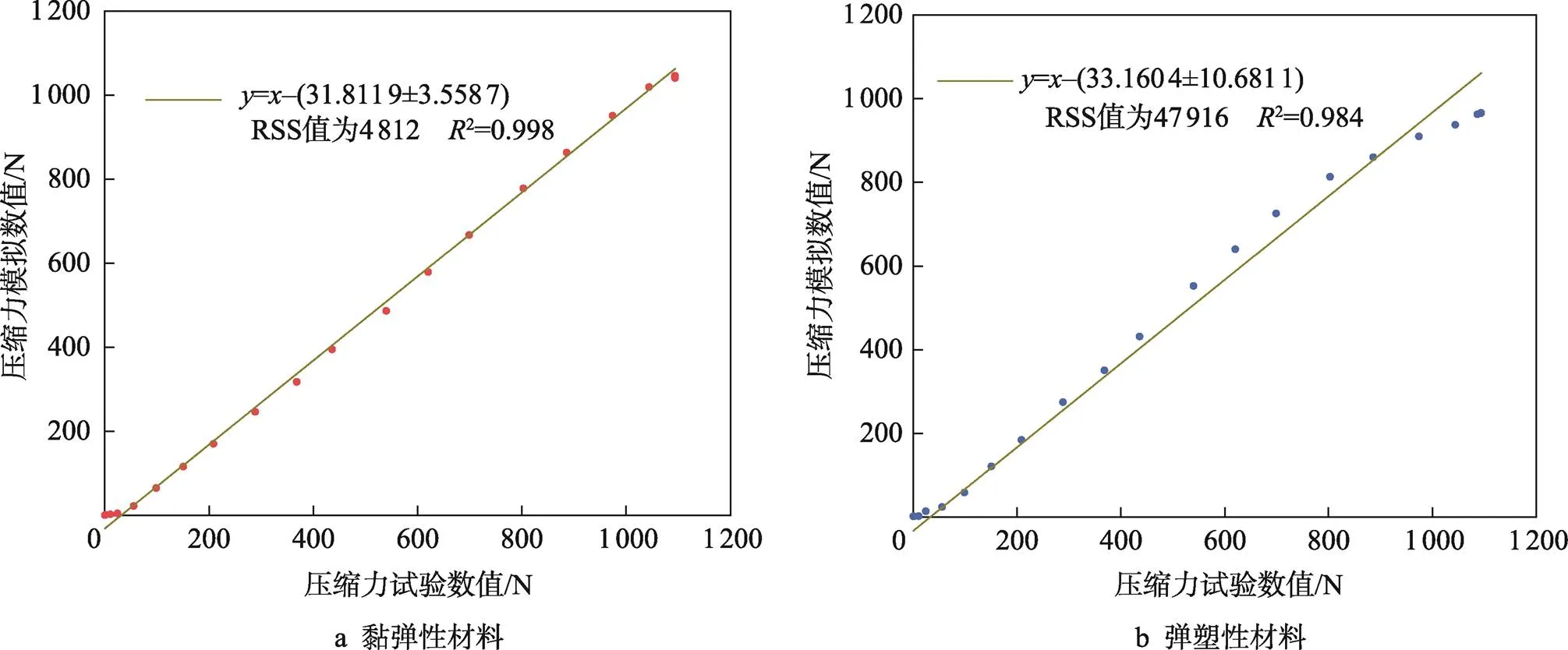
圖11 2種材料仿真誤差分析

3 結語

1）本研究建立了Maxwell黏彈性材料本構模型，并且驗證了該模型用于表征梨類果實非線性流變特性的準確性。基于黏彈性材料的果實仿真模型與傳統彈塑性材料仿真模型進行對比，其誤差減小了7%。說明在靜態壓縮試驗中使用黏彈性材料能更好地表征水果生理特性。

2）根據von Mises等效應力分布可以確定梨果實受損的主要應力位置和大小。當應力值超過0.3 MPa時會發生不可恢復的變形，可將這一數值作為損傷判定的閾值。

3）皇冠梨果實在靜態壓縮位移為13～17 mm時出現破裂，最大壓縮力為1 098 N。為避免發生永久性損傷，建議果實承受靜載力不應超過161.21 N，一次垂直疊放的果實不應超過40層。

研究結論可為梨類果實機械化采摘設備的改進和果實的包裝堆碼、儲存運輸提供一定的理論指導。

[1] 侯煜廬, 趙俊曄. 2020年中國水果市場形勢分析與后市展望[J]. 農業展望, 2021, 17(4): 3-8.

HOU Yu-lu, ZHAO Jun-ye. Analysis of China's Fruits Market Situation in 2020 and Its Future Prospects[J]. Agricultural Outlook, 2021, 17(4): 3-8.

[2] MIRAEI ASHTIANI S H, SADRNIA H, MOHAMMADINEZHAD H, et al. FEM-Based Simulation of the Mechanical Behavior of Grapefruit under Compressive Loading[J]. Scientia Horticulturae, 2019, 245: 39-46.

[3] 王志華, 王文輝, 姜云斌, 等. 不同采收期對蘋果常溫貯藏品質和衰老的影響[J]. 農業工程學報, 2020, 36(7): 300-306.

WANG Zhi-hua, WANG Wen-hui, JIANG Yun-bin, et al. Effects of Different Harvesting Periods on the Storage Quality and Senescence of Apple at Room Temperature[J]. Transactions of the Chinese Society of Agricultural Engineering, 2020, 36(7): 300-306.

[4] LI Zhi-guo, ANDREWS J, WANG Yu-qing. Mathematical Modelling of Mechanical Damage to Tomato Fruits[J]. Postharvest Biology and Technology, 2017, 126: 50-56.

[5] LI Zhi-guo, WANG Yu-qing. A Multiscale Finite Element Model for Mechanical Response of Tomato Fruits[J]. Postharvest Biology and Technology, 2016, 121: 19-26.

[6] Wang L, Zhang Q, Song H, et al. Mechanical Damage of ‘Huangguan’ Pear Using Different Packaging under Random Vibration[J]. Postharvest Biology and Technology, 2022, 187: 111847.

[7] Stropek Z, Go?acki K. Bruise Susceptibility and Energy Dissipation Analysis in Pears under Impact Loading Conditions[J]. Postharvest Biology and Technology, 2020, 163: 111120.

[8] Opara U L, Fadiji T. Compression Damage Susceptibility of Apple Fruit Packed Inside Ventilated Corrugated Paperboard Package[J]. Scientia Horticulturae, 2018, 227: 154-161.

[9] SADRNIA H, AUTHOR E M, RAJABIPOUR A, et al. Internal Bruising Prediction in Watermelon Compression Using Nonlinear Models[J]. Journal of Food Engineering, 2008, 86(2): 272-280.

[10] AHMADI E, GHASSEMZADEH H, SADEGHI M, et al. The Effect of Impact and Fruit Properties on the Bruising of Peach[J]. Journal of Food Engineering, 2010, 97(1): 110-117.

[11] ZULKIFLI N, HASHIM N, HARITH H, et al. Finite Element Modelling for Fruit Stress Analysis - a Review[J]. Trends in Food Science & Technology, 2020, 97: 29-37.

[12] Celik H K. Determination of Bruise Susceptibility of Pears (Ankara Variety) to Impact Load by Means of FEM-Based Explicit Dynamics Simulation[J]. Postharvest Biology and Technology, 2017, 128: 83-97.

[13] SALARIKIA A, ASHTIANI S M, GOLZARIAN M R, et al. Finite Element Analysis of the Dynamic Behavior of Pear under Impact Loading[J]. Information Processing in Agriculture, 2017, 4 (1): 64-77.

[14] 王維, 劉東琴, 王佩. 果品分級檢測技術的研究現狀及發展[J]. 包裝與食品機械, 2016, 34(6): 55-58.

WANG Wei, LIU Dong-qin, WANG Pei. Status and Development of Fruit Detection of Mechanical Classification[J]. Packaging and Food Machinery, 2016, 34(6): 55-58.

[15] 曹旭東, 胡洋, 許騰宇, 等. 定則振動系統下黃冠梨振動特性及損傷研究[J]. 包裝工程, 2017, 38(17): 102-107.

CAO Xu-dong, HU Yang, XU Teng-yu, et al. Vibration Characteristic and Injury of Huangguan Pearunder Stationary Vibration System[J]. Packaging Engineering, 2017, 38(17): 102-107.

[16] ASABE S368, Compression Test of Food Materials of Convex Shape[S].

[17] ASTM E328, Standard Test Methods for Stress Relaxation for Materials and Structures[S].

[18] 張琦, 李金花, 胡盼盼, 等. 梨品種果實不同部位石細胞特性研究[J]. 塔里木大學學報, 2014, 26(1): 99-104.

ZHANG Qi, LI Jin-hua, HU Pan-pan, et al. Studies on Characteristics of Stone Cell in Different Parts of Pear Fruits[J]. Journal of Tarim University, 2014, 26(1): 99-104.

[19] Kim G W, Kim M S, SAGARA Y, et al. Determination of the Viscoelastic Properties of Apple Flesh under Quasi-Static Compression Based on Finite Element Method Optimization[J]. Food Science and Technology Research, 2008, 14(3): 221-231.

[20] 王俊, 王劍平, 蔣亦元, 等. 梨肉松弛特性各向差異研究[J]. 農業工程學報, 2002, 18(4): 123-126.

WANG Jun, WANG Jian-ping, JIANG Yi-yuan, et al. Anisotropic Relaxation Properties of Pear[J]. Transactions of the Chinese Society of Agricultural Engineering, 2002, 18(4): 123-126.

[21] AHMADI E, BARIKLOO H, KASHFI M. Viscoelastic Finite Element Analysis of the Dynamic Behavior of Apple under Impact Loading with Regard to Its Different Layers[J]. Computers and Electronics in Agriculture, 2016, 121: 1-11.

[22] 師廣強, 田勇浩, 吳建幫, 等. 不同緩沖壓頭下香梨靜壓損傷特性研究[J]. 包裝工程, 2020, 41(1): 51-57.

SHI Guang-qiang, TIAN Yong-hao, WU Jian-bang, et al. Static Pressure Damage Characteristics of Korla Pear under Different Cushioning Head[J]. Packaging Engineering, 2020, 41(1): 51-57.

[23] LI Zhi-guo, YANG Hong-ling, LI Ping-ping, et al. Fruit Biomechanics Based on Anatomy: A Review[J]. International Agrophysics, 2013, 27(1): 97-106.

Static Pressure Mechanical Properties and Simulation of Huangguan Pears

WU Ying-tong1, WU Zi-ming1, ZHANG Li-jun1, SUN Yi-ming1, WANG Li-jun1,2, SONG Hai-yan1,2*

(1. School of Light Industry Science and Engineering, Tianjin University of Science and Technology, Tianjin 300457, China; 2. Key Laboratory of Food Packaging Materials and Technology of China Light Industry, Tianjin 300457, China)

The work aims to establish a relationship model between physiological characteristics and mechanical damage of Huangguan pears to simulate the static pressure process of the fruit. The mechanical properties of fruit materials were studied by material relaxation test and static compression test. The three-dimensional scanning method was used to assist in the establishment of the finite element model of the fruit, and the static load damage process of the fruit was simulated. The Maxwell viscoelastic constitutive model was used to successfully simulate the rheological properties of the fruit. By comparing the static pressure test with the traditional elastic-plastic material model, the error was reduced by 7%, which verified the simulation accuracy. According to the results of von Mises equivalent stress distribution, it was found that the pear would be significantly damaged under static load of 161.21 N. In the above studies, two materials are used to simulate the static compression test, which further verifies the reliability of the numerical simulation method to simulate the static process of the fruit. It also provides a theoretical basis for the mechanized picking, storage, packaging and processing of Huangguan pears.

finite element simulation; relaxation experiment; constitutive model; static pressure test; fruit damage

TB485.3

A

1001-3563(2023)19-0050-08

10.19554/j.cnki.1001-3563.2023.19.007

2023-04-06

國家自然科學基金（32202116）

責任編輯：曾鈺嬋