基于三次B樣條平滑的加性風險模型擬合研究

唐璐薇,呂 超,文秋月,韋程東

(1.廣西科技師范學院 數學與計算機科學學院,廣西 來賓 546100; 2.柳州市婦幼保健院,廣西 柳州 545000; 3.南寧師范大學 數學與統計學院,廣西 南寧 530000)

0 引 言

生存分析是一種既考慮結果又考慮生存時間的統計方法,其可充分利用截尾數據所提供的不完全信息,對生存時間的分布特征進行描述,以及對影響生存時間的主要因素進行分析.比例風險模型是研究生存數據最廣泛的統計半參數模型之一[1-2],但其對數據的擬合效果并不理想.因此,需要我們尋求一個比例風險模型的替代模型,即加性風險模型.與比例風險模型不同的是,加性風險模型是假設基底風險函數與協變量之間的一個加性結構.在實際應用中,加性風險模型對數據的擬合效果更好,正是由于它這一特性,加性風險模型中的回歸參數更容易解釋實際意義[3-4].

目前,運用不同模型對數據進行擬合的研究有很多.顧劉金首先利用Cox模型對數據進行擬合,但由于Cox模型具有比例風險性,故基于SPSS采用Logistic回歸模型對數據進行擬合得出結果[5].Jardim等利用微分方程模型對葡萄牙的COVID-19相關數據進行擬合分析,同時指出該方法可針對不同的流行病學數據進行擬合分析[6].此外,很多學者也運用B樣條擬合方法進行研究.曾卓等提出了基于三次B樣條小波的曲線擬合方法,該方法行之有效,為曲線擬合提供了一種兼顧擬合精度、光順性與加工精度的方法[7].張永華等針對傳統幾何軌跡跟蹤算法切向角獲取依賴高精度慣導設備的問題,提出了基于三次B樣條曲線擬合的軌跡跟蹤算法,該算法有效解決了傳統算法的問題[8].Bi等基于全局擬合法的缺點,提出一種通用、快速的B樣條誤差擬合方案,該方法與傳統的擬合方法相比,顯著地提高了工作效率[9].龐宇等提出一種結合幅度系數法和波形特征法對脈搏波采用三次B樣條曲線擬合的血壓檢測算法,該算法能夠提高特征點的準確率[10].蘆穗豪等提出一種基于改進麻雀搜索算法的B樣條曲線擬合方法,旨在利用最少控制點高效地達到曲線擬合的目標精度,進而提升傳統建模方法的精度和效率[11].徐超清等基于神經纖維走向信息考量的問題,提出一種基于B樣條擬合與回歸模型的腦神經纖維聚類方法,該方法在功能區層面的聚類可以更有效地分割出具有解剖學結構的腦神經纖維[12].

上述研究大多是運用傳統的模型對生存數據進行分析,且運用三次B樣條平滑函數對生存數據進行擬合,而利用加性風險模型進行相關研究的較少.本文運用三次B樣條擬合方法,研究經藥物治療后白血病患者的生存周期與實際情況的擬合程度,從而判斷藥物治療的有效性,并運用單變量加性風險模型和多變量加性風險模型找出對生存時間影響顯著的協變量,作出生存時間的預測圖,從而為決策者提供一定的參考依據.

1 模型介紹

1.1 加性風險模型

假設研究隊列數據包含N個獨立的樣本,設T為失效時間,C為相應的截尾時間,Z(t)(0≤t≤τ)為協變量過程的向量,其中τ<∞表示后續時間.由于數據右刪失,所以只能觀察X和δ,其中X=min(T,C′)和δ=I(T≤C).用Yi(t)=I(Ti≥t)表示歷險過程的示性函數,Ni(t)=ΔiI(Ti≤t)表示計數過程,這里I(·)是示性函數.假定T和C是條件獨立的,可考慮以下加性風險模型.當給定協變量Zi(t)時,失效時間T的風險函數為:

(1)

其中,λ0(t)為一個未指定的基底風險函數,β=(β1,β2,…,βp)為未知回歸參數的p維向量.

1.2 三次B樣條插值函數

B樣條曲線是在Bezier曲線基礎上發展起來的,其克服了Bezier曲線整體控制性所帶來的不方便.它是通過逼近一組控制點生成的曲線,計算公式為:

(2)

其中,pk為輸入的一組數據中的第k個數據點;Nk,d為B樣條混合函數,這里為加性風險模型,k為第k個混合函數,d為次數.本文采用三次B樣條插值函數進行平滑,即d=3.

B樣條曲線保留了Bezier曲線的優勢,同時曲線在拼接時又比Bezier曲線方便,在修改時可做局部修改,而且在調整某一控制點時不會影響整條曲線的趨勢.其性質主要有以下幾點:

(1)局部性.K階B樣條曲線上的一點至多與k個控制頂點有關,與其他控制頂點無關.

(2)幾何不變形.B樣條曲線的形狀和位置與坐標系的選擇無關,不管坐標系如何變化,B樣條曲線的形狀仍保持原樣.

(3)凸包性.與Bezier曲線一樣,B樣條曲線落在Pi構成的凸包中,其凸包區域小于或等于同一組控制頂點定義的Bezier曲線凸包區域.

2 白血病數據的三次B樣條平滑

常見的生存數據處理模型有比例風險模型(Cox模型)、加性風險模型等,二者在處理生存數據上都有一定的優勢.下面給出Cox模型和加性風險模型對白血病數據分析的結果.

(1)Cox模型數據擬合.根據已知白血病數據中的自變量,選取6個自變量作為協變量:age(年齡)、sex(性別)、 ph.ecog(ECOG評分)、ph.karno(醫師的Karnofsky評分)、meal.cal(用餐時消耗的卡路里)、wt.loss(最近6個月的體重減輕),并運用Cox模型對其進行分析,結果見表1.

表1 Cox模型對6個協變量的分析

由表1可知,性別和ECOG評分與生存時間顯著相關,且P值遠小于0.05,模型擬合效果較好.

(2)加性風險模型數據擬合.為與Cox模型擬合效果進行對比,下面運用加性風險模型對上述6個協變量進行分析,查看加性風險模型對數據的擬合效果及相關性,結果見表2.

表2 加性風險模型對6個協變量的分析

由表2可知,加性風險模型對數據的擬合效果與Cox模型一樣,性別和ECOG評分與生存時間顯著相關,且P值遠小于0.05,模型的擬合效果較好.但加性風險模型還給出了對生存時間的整體方差解釋率,更進一步說明了該模型對數據的擬合效果.因此,本文在三次B樣條平滑函數下,運用加性風險模型來研究白血病的治療數據,從而給出相關結論.

2.1 三次B樣條平滑

為減輕協變量對術后患者生存時間的影響,本文利用三次B樣條平滑法對受干擾的協變量進行平滑,以消除協變量對響應變量即生存時間的影響.下面首先討論利用三次B樣條平滑法對受干擾的加性風險模型中的協變量進行平滑,然后討論單變量加性風險模型和多變量加性風險模型中協變量與生存時間的關系.三次B樣條平滑過程分以下幾點討論:

(1)59歲以下的男性,其生存時間與用餐時消耗的卡路里、最近6個月體重減輕的關系見圖1.其中,第一行指定的平滑系數分別為k=3,k=5;第二行指定的平滑系數分別為k=5,k=7.由圖1可知,從整體看,白血病患者的生存時間隨著用餐時消耗卡路里的增加而增加,但不同平滑程度的選擇影響了局部趨勢的解釋,特別是不同年齡生存時間的變化趨勢是不同的,且最近6個月的體重減輕對生存時間的影響也較明顯.

圖1 59歲以下男性兩協變量與生存時間的關系

(2)59歲以上的男性,其余條件與(1)相同,得到的結果見圖2.由圖2可知,59歲以上的男性,隨著年齡的增加,其消耗的卡路里逐漸降低,而相對(1)來說,近6個月的體重減輕呈細微的增加趨勢.

(3)59歲以下的女性,其余條件與(1)相同,結果見圖3.由圖3可知,59歲以下的女性,隨著年齡的增加,其消耗的卡路里趨于平穩,而隨著近6個月體重減輕的越來越多,生存時間呈先下降后上增的趨勢.

圖3 59歲以下女性兩協變量與生存時間的關系

(4)59歲以上的女性,其余條件與(1)相同,結果見圖4.由圖4可知,59歲以上的女性,從整體看與圖3中59歲以下的女性分析結果相似,但在平滑系數k=7時,脂肪消耗量發生細微變化,隨著脂肪消耗的增多,生存時間呈細微上增的趨勢.

通過三次B樣條平滑對年齡(age)、性別(sex)、ECOG評分(ph.ecog,0=好,5=死)、醫師的Karnofsky評分(ph.karno,0=差,100=好)、用餐時消耗的卡路里(meal.cal)和最近6個月的體重減輕(wt.loss)等6個協變量中受干擾的協變量進行平滑后,暫時不能確定哪些協變量對生存時間的影響顯著.下面研究生存時間的單變量加性風險模型,并根據研究結果選擇協變量進行多變量的加性風險模型研究,以探索這些協變量對生存時間的影響.

2.2 單變量加性風險模型研究

選擇協變量:年齡(age)、性別(sex)、ECOG評分(ph.ecog,0=好,5=死)、醫師的Karnofsky評分(ph.karno,0=差,100=好)、用餐時消耗的卡路里(meal.cal)和最近6個月的體重減輕(wt.loss),并用這些協變量擬合加性風險模型,結果見表3.其中,s()為運用三次B樣條平滑后的符號表示.

表3 單變量加性風險模型擬合結果

由表3可知,性別、年齡、ph.karno和ph.ecog變量具有較好的統計學意義(P<0.05),說明它們對生存時間的影響是顯著的.此外,年齡和ph.ecog具有正β系數,而性別和ph.karno具有負β系數.因此,年齡較大和ph.ecog較高與事件發生率呈正相關,而女性(sex=2)和ph.karno則與事件發生率呈負相關,即年齡和ph.ecog是死亡的危險因素,女性性別和醫師的Karnofsky評分是死亡的保護因素.

2.3 多變量加性風險模型研究

為研究性別、年齡、ph.ecog和ph.karno如何共同影響生存時間,本文利用多變量加性風險模型進行分析,結果見表4.

表4 多變量加性風險模型擬合結果

由表4可知,加性風險模型對生存時間的整體方差解釋率達78.5%,擬合效果較好.在多元加性風險模型分析中,協變量性別和ph.ecog保持著顯著性(P<0.05),但協變量年齡和ph.karno不顯著(年齡:P=0.171 226,ph.karno:P=0.186 82均大于0.05).

性別的P值為0.000 712,風險比HR=exp(coef)=0.56,表明患者的性別與死亡風險降低之間有很強的關系.在保持其他協變量不變的前提條件下,女性(sex=2)相比男性,其死亡風險低44%.可見,性別為女性與良好的預后相關.

同樣,ph.ecog的P值為0.000 323,風險比HR=1.88,表明ph.ecog值與死亡風險增加之間有很強的關系.相比之下,年齡的P值為0.171 226,風險比HR=exp(coef)=1.01,95%置信區間為0.99～1.03.由于HR的置信區間為1,因此該結果表明,在調整ph.ecog值和患者性別后,年齡對HR差異的貢獻較小,且不顯著.

為研究白血病患者治療的生存數據與治療的關系,以及白血病治療的有效性,針對上述對協變量的研究,本文選取性別和ph.ecog作為協變量來擬合加性風險模型.使用K-M估計方法,以存活天數為橫坐標,以生存率為縱坐標,給出估計的生存率和生存率的置信區間,見圖5.

圖5 存活天數與生存率的關系

如圖5所示,隨著存活天數的增多,術后存活率也逐漸下降,這與自然規律相符.此外,由上述對多變量加性風險模型協變量的分析可知,性別和ph.ecog對模型具有顯著影響.性別和ph.ecog對生存時間和生存率的影響見圖6.

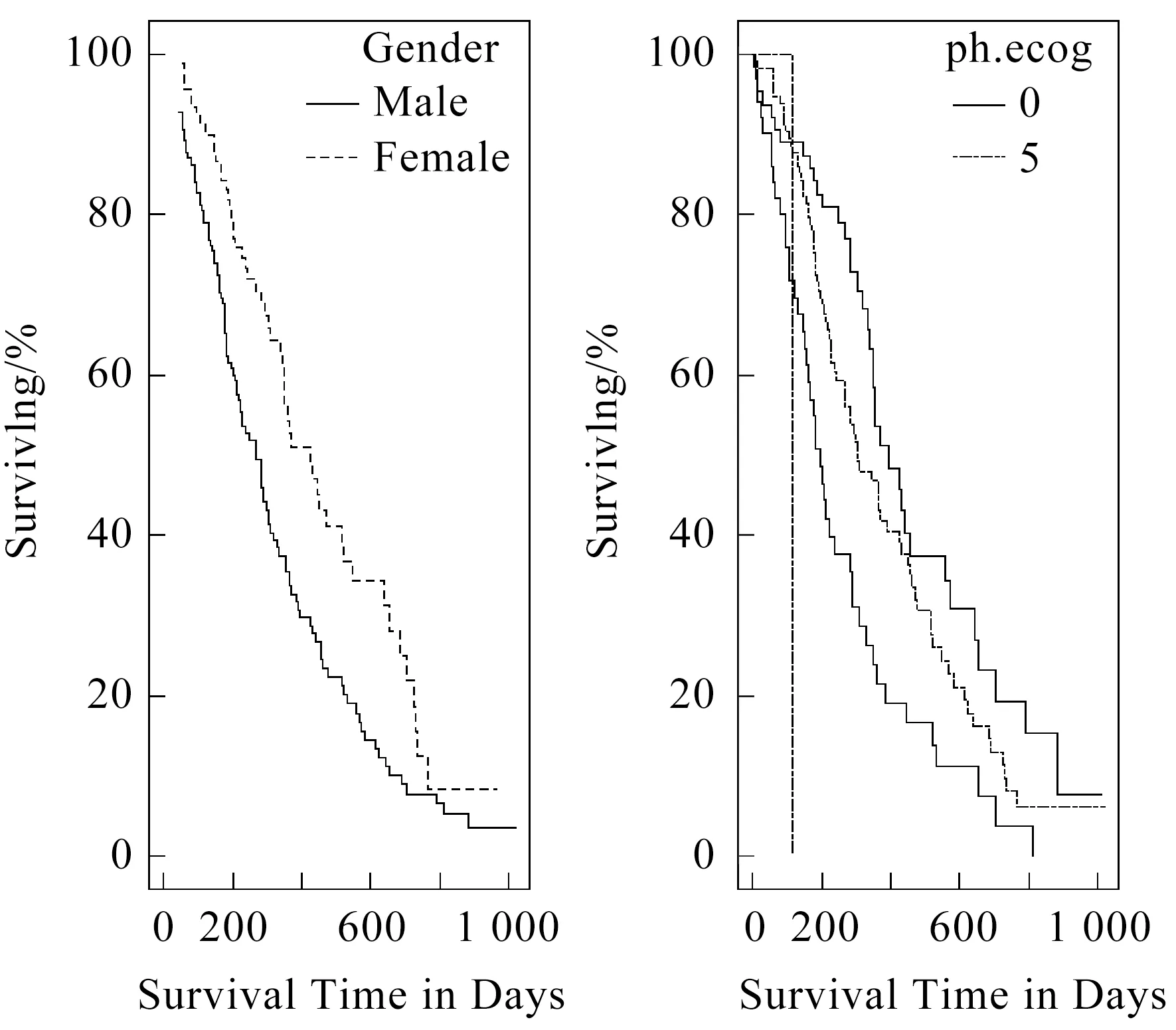
圖6 性別和ph.ecog對生存時間的影響

由圖6可知,女性的整體生存率高于男性,在ph.ecog評分表中對應的評分為5,且生存率隨著生存時間的變化逐漸下降.但這種差異是否顯著并不確定,還需要進行統計檢驗,檢驗結果見表5.

表5 性別和ph.ecog差異顯著性檢驗

由表5可知,將性別和ph.ecog綜合考慮,得到的P值遠小于0.05,說明男女之間以及不同的ECOG評分,其生存率是有差異的.

與K-M生存曲線不同的是,加性風險模型擬合曲線得到的生存率是在運用三次B樣條平滑其他協變量后所預測的生存率,并不是實際觀察到的生存率.加性風險模型擬合生存率曲線見圖7.

圖7 加性風險模型擬合生存率曲線

由圖7可知,預測患者的生存率隨著生存時間的增多而逐漸下降,與使用K-M估計方法對白血病患者的生存時間和生存率所作出的曲線趨勢一致.由于本文研究的是白血病治療數據,涉及對醫療效果的評價,因此選擇精確度較高,且對解決高度非線性預測問題有突出能力的加性風險模型來對數據進行擬合是可行的.

3 結 論

本文研究的白血病數據涉及分析白血病藥物治療的效果,精度要求較高,需要一個能夠對生存數據進行分析且擬合效果較好的模型.本文利用加性風險模型對其進行擬合研究,并通過圖形展示患者生存時間的變化.為避免數據缺失給加性模型研究帶來誤差,利用三次B樣條平滑函數對其進行平滑,并對刪失的數據進行處理,以避免造成對已有數據的影響.通過對數據分析可知,不同平滑程度對擬合效果影響不大,不能直接表達哪些協變量對生存時間影響顯著.本文不足之處在于運用三次B樣條平滑函數對加性風險模型進行平滑后,只對白血病治療數據進行研究,沒有考慮到其他疾病數據的擬合效果是否一樣.此外,針對白血病的治療數據也只運用了加性風險模型對其進行研究,沒有運用其他模型進行擬合.今后的研究將針對這兩個問題進行深入探討,從多方面進行生存分析研究.