傳動機構用四點接觸球軸承優(yōu)化設計
王亞濤,邱明,2,趙濱海,田凱文,王會杰
(1.河南科技大學 機電工程學院,河南 洛陽 471003;2.機械裝備先進制造河南省協同創(chuàng)新中心,河南 洛陽 471003;3.洛陽軸承研究所有限公司,河南 洛陽 471039)
四點接觸球軸承作為傳動機構的關鍵部件,高速運轉時內部運動關系十分復雜, 其性能直接影響整機的工作效率、穩(wěn)定性和可靠性, 因此對四點接觸球軸承進行優(yōu)化設計具有重要意義。
目前,國內外專家在軸承優(yōu)化設計方面開展了許多工作:文獻[1]通過建立擬動力學模型,利用功效系數法,以旋滾比、基本額定動載荷、摩擦力矩和軸向剛度為目標函數對軸承主參數進行優(yōu)化;文獻[2]以額定動載荷的負數為目標函數建立數學模型,運用MATLAB優(yōu)化工具箱對混合陶瓷球軸承進行優(yōu)化設計;文獻[3]借助MATLAB將梯度下降法應用到滾動軸承的優(yōu)化設計中;文獻[4]以額定動載荷、支承剛度、旋滾比為目標,基于NSGA-II遺傳算法進行多目標優(yōu)化設計;文獻[5]建立可靠性評估模型對滾動軸承進行可靠性優(yōu)化設計;文獻[6]采用線性加權法,以額定動載荷最大、摩擦力矩及旋滾比最小為優(yōu)化目標,對汽車空調用雙列角接觸球軸承進行優(yōu)化設計;文獻[7]建立了角接觸球軸承的接觸概率模型,從角接觸球軸承在不同載荷下球面接觸概率的角度考慮軸承的優(yōu)化設計;文獻[8]基于RomaxCLOUD對某薄壁角接觸球軸承進行優(yōu)化設計,建立了以剛度、最小油膜厚度、壽命為目標的優(yōu)化數學模型,提出了薄壁角接觸球軸承的多目標優(yōu)化方法;文獻[9]通過正交試驗法設計試驗,運用多目標函數的功效系數法對角接觸球軸承參數進行優(yōu)化設計。
上述文獻主要以軸承的額定動載荷、支承剛度、旋滾比、摩擦力矩為單目標或者多目標進行優(yōu)化設計,研究對象一般是角接觸球軸承和深溝球軸承,對于四點接觸球軸承的優(yōu)化設計問題研究較少,且現有優(yōu)化設計中很少考慮軸承動態(tài)特性。本文采用NSGA-II遺傳算法對四點接觸球軸承結構參數進行優(yōu)化,并將擬靜力學模型引入四點接觸球軸承的優(yōu)化設計中,研究軸承接觸角的變化。
1 四點接觸球軸承優(yōu)化設計數學模型
滾動軸承在運轉過程中常見的失效形式為疲勞失效,為防止軸承失效,延長使用壽命,要求其具有較高的承載能力,即額定動載荷[10];同時,軸承在運轉過程中各零件均會產生摩擦,從而產生摩擦力矩[11],影響軸承使用性能。鑒于此,本文主要針對四點接觸球軸承的額定動載荷和摩擦力矩進行分析。
1.1 四點接觸球軸承的優(yōu)化模型
以四點接觸球軸承的額定動載荷和摩擦力矩為目標函數,通過線性加權法建立優(yōu)化模型,目標函數F為
(1)
γ=(Dwcosα)/Dpw,
式中:γ1,γ2為權重系數,根據變量對軸承性能的影響進行取值;Cr為徑向基本額定動載荷[12];M為軸承總摩擦力矩;bm為額定動載荷系數,對于四點接觸球軸承取1.3;fc為與軸承結構相關的系數;α為接觸角;Z為鋼球數量;Dw為鋼球直徑;λ為額定動載荷修正系數,對于四點接觸球軸承取0.90;fi,fe分別為內、外圈溝曲率半徑系數;Dpw為球組節(jié)圓直徑。
根據滾動軸承的摩擦特點,本文主要考慮的因素有[13]:彈性滯后引起的摩擦力矩、差動滑動引起的摩擦力矩、自旋滑動引起的摩擦力矩、潤滑劑黏性引起的摩擦力矩。
彈性滯后引起的摩擦力矩ME為(下標i,e分別表示內圈和外圈,下同)
(2)
式中:βa為彈性滯后系數,對于軸承鋼取0.007;K為橢圓率;u為初始游隙;∑ρi(e)為兩接觸面曲率和;Qi(e)j為第j個鋼球的接觸載荷;F(φ)i(e)為第一類橢圓積分;E(φ)i(e)為第二類橢圓積分;ai(e)為接觸橢圓長半軸;bi(e)為接觸橢圓短半軸;E′為當量彈性模量;Eb為鋼球彈性模量;Ei(e)為套圈彈性模量;νb為鋼球材料的泊松比;νi(e)為套圈材料的泊松比。
差動滑動引起的摩擦力矩MD為
(3)
式中:fs為滑動摩擦因數,對于軸承鋼取0.08。
自旋滑動引起的摩擦力矩MS為
(4)
式中:αi(e)j為實際接觸角。
潤滑劑黏性引起的摩擦力矩Moil為
(5)
式中:αoil為潤滑油黏壓系數;S為潤滑充分系數,可取油膜潤滑系數;Hi(e)為油膜厚度。
則總摩擦力矩M為
M=ME+MD+MS+Moil。
(6)
1.2 設計變量及尺寸約束
設計變量分別為內、外圈溝曲率半徑系數fi和fe,鋼球直徑Dw,球組節(jié)圓直徑Dpw,原始接觸角α0,表達式為
X=[x1,x2,x3,x4,x5]T=[fi,fe,Dw,Dpw,α0]T。
1.2.1 溝道半徑約束
溝曲率半徑系數與四點接觸球軸承的摩擦力矩、接觸角等密切相關,根據經驗公式,軸承內外圈溝道半徑應不小于0.515Dw且不大于0.540Dw,因此該模型滿足以下約束
0.515Dw≤fiDw≤0.540Dw,
(7)
0.515Dw≤feDw≤0.540Dw,
(8)
約束條件可表示為
h1(x)=x1-0.515≥0,
(9)
h2(x)=0.540-x1≥0,
(10)
h3(x)=x2-0.515≥0,
(11)
h4(x)=0.540-x2≥0。
(12)
1.2.2 鋼球直徑約束
根據設計經驗及技術要求,鋼球直徑的取值范圍為
0.23(D-d)≤Dw≤0.32(D-d),
(13)
約束條件可表示為
h5(x)=x3-0.23(D-d)≥0,
(14)
h6(x)=0.32(D-d)-x3≥0,
(15)
式中:D為軸承外徑;d為軸承內徑。
1.2.3 球組節(jié)圓直徑約束
為保證四點接觸球軸承鋼球的靈活度,四點接觸球軸承的球組節(jié)圓直徑和軸承直徑的差值應保持在一定的范圍內。球組節(jié)圓直徑取值范圍為
0.5(D+d)≤Dpw≤0.515(D+d),
(16)
約束條件可表示為
h7(x)=x4-0.5(D-d)≥0,
(17)
h8(x)=0.515(D-d)-x4≥0。
(18)
1.2.4 鋼球數量約束
四點接觸球軸承設計過程中,鋼球數量需滿足的約束方程為
(19)
當Dw≤9.525 mm時,Kz=1.01+2.3/Dw;Dw>9.525 mm時,Kz=1.23,K值可減小到1.15,計算出的Z取較小的整數。
約束條件可表示為
(20)
1.3 四點接觸球軸承的優(yōu)化設計數學模型
通過上述分析,四點接觸球軸承的優(yōu)化設計數學模型為
(21)
依據建立的四點接觸球軸承優(yōu)化設計數學模型,本文借助NSGA-II遺傳算法對軸承進行優(yōu)化設計,采用快速非支配排序算法,引用精英保留策略,降低計算復雜度。首先,把設計變量fi,fe,Dw,Dpw,α0記為個體,隨機產生初始種群;其次,對個體求帕雷托(pareto)解,非支配排序后通過遺傳算法的選擇、交叉、變異3個基本操作得到第一代子代種群;然后,從第二代開始,將父代種群與子代種群合并,進行快速非支配排序,同時對每個非支配層中的個體進行擁擠度計算,依據非支配關系和個體擁擠度建立的適應度函數選取合適的個體組成新的父代種群;最后,按照一定規(guī)則從種群生成新的父代種群Cn+1實現精英保留策略,經過實數編碼的交叉操作和多項式變異,通過錦標賽法進行選擇操作,尋求目標函數的最優(yōu)解。
2 四點接觸球軸承擬靜力學模型
當四點接觸球軸承工作接觸角小于墊片角時,鋼球與內、外溝道間發(fā)生多點接觸,接觸區(qū)會發(fā)生大的滑動摩擦,易造成軸承提前失效[14]。因此要建立擬靜力學模型研究四點接觸球軸承動態(tài)性能,分析優(yōu)化結構參數后的軸承在運轉過程中接觸角的變化。下面主要從鋼球中心和溝曲率中心的幾何位置關系、鋼球在任意方位角的受力平衡、套圈的受力平衡三方面建立擬靜力學模型。
2.1 鋼球中心和溝曲率中心的幾何位置關系
以四點接觸球軸承中心為原點,軸向中心線為x軸建立坐標系,四點接觸球軸承各鋼球的角位置示意圖如圖1所示,圖中:j為鋼球的序號;ψj為第j個鋼球的位置角,ψj=2π(j-1)/Z。
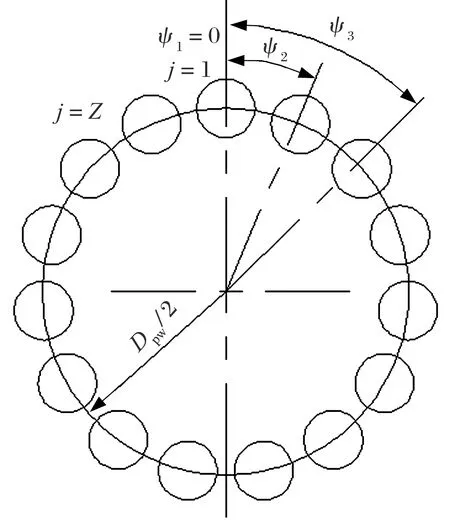
圖1 鋼球角位置示意圖
軸承受載前,內外溝曲率中心的距離為l0,四點接觸球軸承在離心力和陀螺力矩作用下,鋼球與內外溝道的接觸角發(fā)生變化,鋼球中心與內、外溝曲率中心不再共線,則載荷作用前后角位置ψj處鋼球中心與內、外溝曲率中心的位置關系如圖2所示。
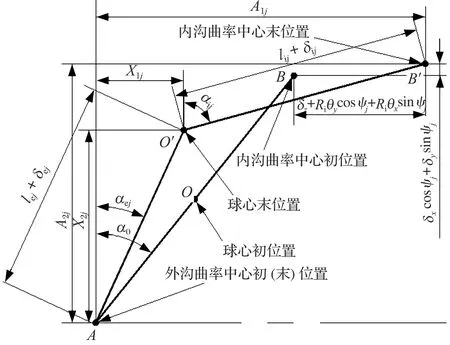
圖2 受載前后鋼球中心與內、外溝曲率中心相對位置
由圖2可以看出,受載前鋼球中心與內、外溝曲率中心的距離lij,lej分別為
lij=(fi-0.5)Dw,
(22)
lej=(fe-0.5)Dw。
(23)
任意角位置ψj處內、外溝曲率中心的軸向距離A1j和徑向距離A2j分別為
A1j=l0sinα0+δz+Riθxsinψj+Riθycosψj,
(24)
A2j=l0cosα0+δxcosψj+δysinψj,
(25)
Ri=Dpw/2+(fiDw-Dw/2)cosα0,
(26)
式中:δx,δy,δz為內圈溝道相對于外圈溝道分別沿x,y,z方向產生的偏轉位移;Ri為內溝道轉動半徑;θx,θy分別為繞x,y軸中心線方向產生的偏轉角度。
根據勾股定理可推得
(A1j-X1j)2+(A2j-X2j)2(lij+δij)=0,
(27)
(28)
式中:X1j,X2j分別為受載后鋼球中心到外溝曲率中心的軸向距離和徑向距離;δij,δej分別為受載后內、外圈溝道的法向變形。
2.2 鋼球在任意方位角的受力平衡方程
在角位置ψj處鋼球的受力分析如圖3所示。
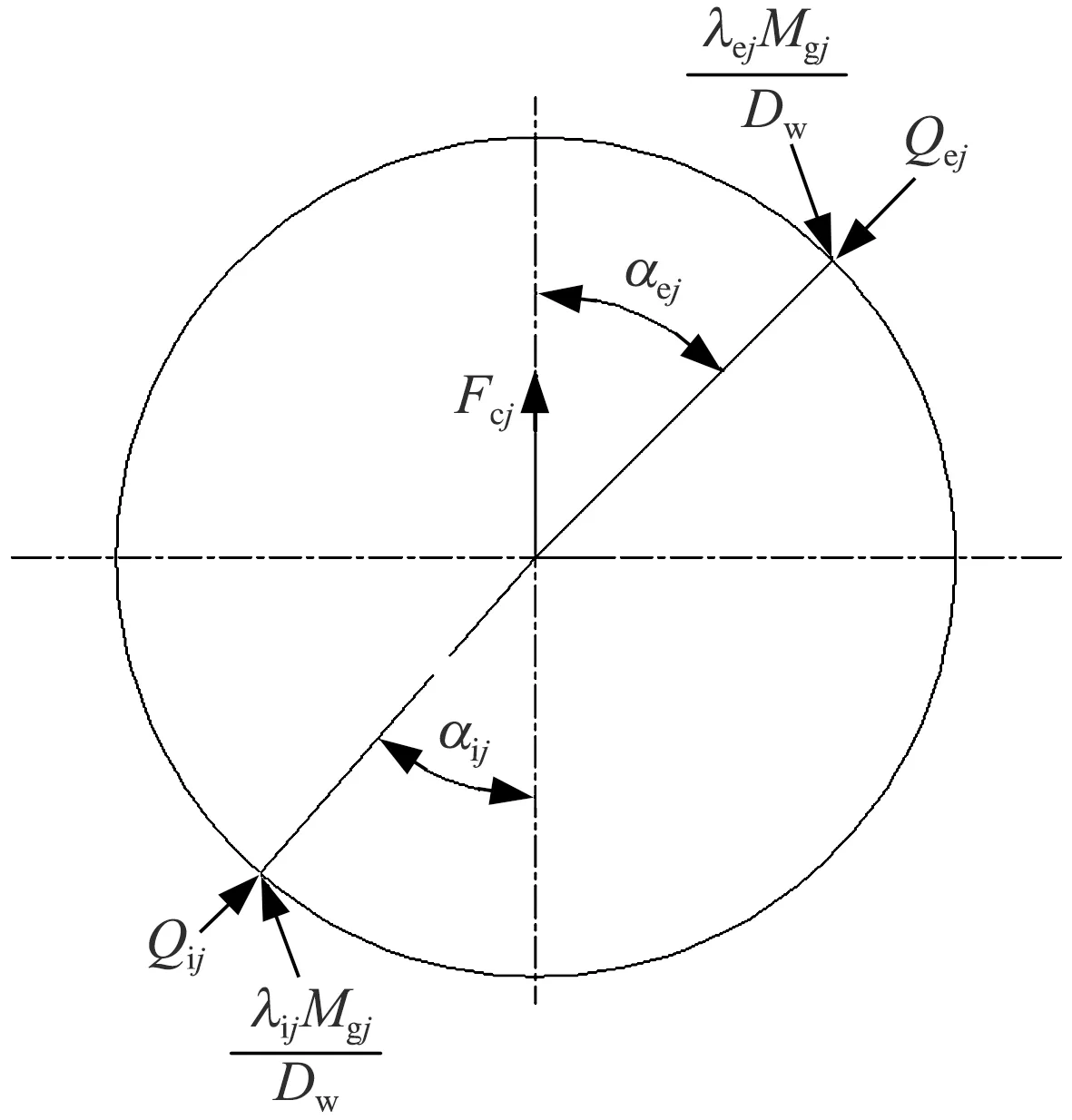
圖3 角位置ψj處鋼球的受力分析
角位置ψj處鋼球與內、外溝道的實際接觸角關系為
(29)
(30)
(31)
(32)
角位置ψj處內外圈載荷-位移關系為
Qij=Kijδij1.5,
(33)
Qej=Kejδej1.5,
(34)
式中:Qij,Qej分別為內、外圈與鋼球的法向接觸載荷;Kij,Kej分別為內、外圈溝道載荷-位移系數。
第j個鋼球所受到的離心力Fcj和陀螺力矩Mgj為
(35)
Mgj=JωmjωRjsinβj,
(36)
式中:m為單個鋼球的質量;ωmj為鋼球公轉角速度;J為鋼球轉動慣量;ωRj為鋼球自轉角速度;βj為鋼球姿態(tài)角。
角位置ψj處鋼球與內、外溝道的摩擦力為
Fij=λijMgj/Dw,
(37)
Fej=λejMgj/Dw,
(38)
式中:λij,λej分別為內、外溝道控制系數,外溝道控制時取λij=0,λej=2,否則取λij=1,λej=1。
則鋼球的受力平衡方程為
(39)
2.3 套圈的受力平衡方程
根據四點接觸球軸承的平衡條件列出內圈的五自由度平衡方程并借助MATLAB軟件求解,內圈五自由度平衡方程為
(40)
式中:Fx,Fy,Fz分別為軸承受到的沿x,y,z軸的力;My,Mz分別為繞y,z軸的力矩。
3 實例計算
以QJ214型四點接觸球軸承為例,其內、外圈及鋼球材料為GCr15,主要結構參數為:d=70 mm,D=125 mm,寬度B=24 mm,墊片角αs=30°。根據前文對軸承壽命和摩擦力矩的要求并參考設計經驗確定權重系數γ1=0.7,γ2=0.3,NSGA-II遺傳算法中取種群數量pop為100、迭代次數gen為50、交叉概率為0.9、變異概率為0.05。
在確定軸承基本參數后,以額定動載荷和摩擦力矩為目標函數建立四點接觸球軸承優(yōu)化設計數學模型,應用NSGA-II遺傳算法對四點接觸球軸承結構參數進行優(yōu)化,最后,基于擬靜力學模型,檢驗接觸角和墊片角的大小關系,若墊片角大于接觸角,通過改變內、外溝曲率半徑系數返回建立的約束方程,構成循環(huán),直至滿足設計要求。整個優(yōu)化設計流程如圖4所示。
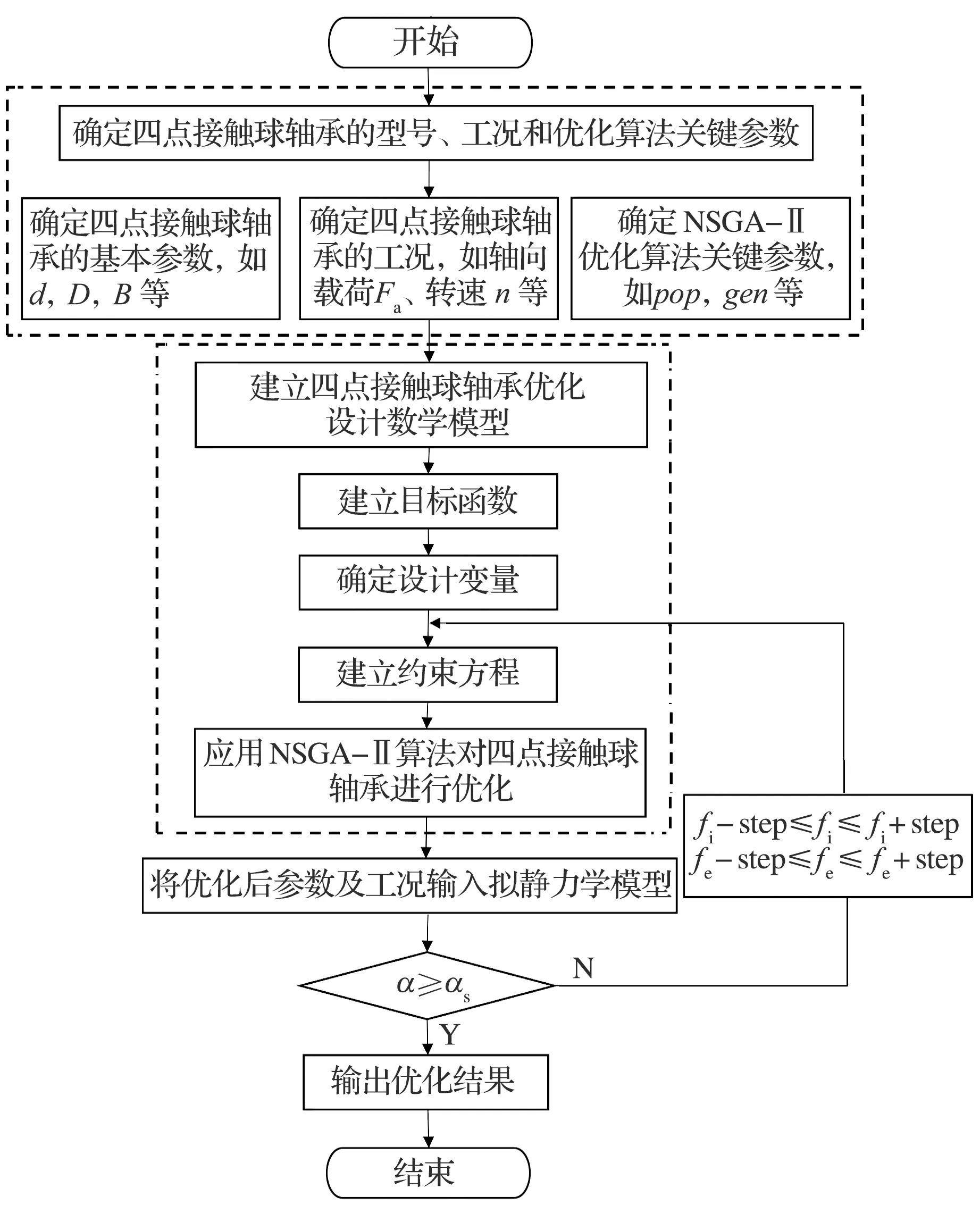
圖4 優(yōu)化設計流程圖
優(yōu)化后四點接觸球軸承的結構參數對比分析見表1,Dw=17.6 mm是優(yōu)化模型得到的最優(yōu)解,考慮到加工因素,為方便軸承進行批量化生產,Dw可根據實際加工條件取規(guī)定標準值。
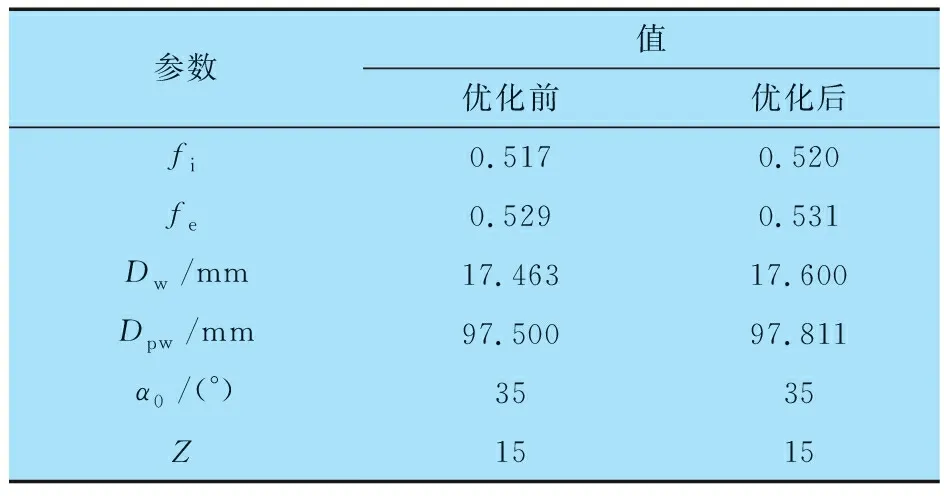
表1 優(yōu)化后四點接觸球軸承的結構參數
將表1中優(yōu)化后的四點接觸球軸承結構參數輸入擬靜力學模型,設定工況:軸向載荷Fa=3 500 N,徑向載荷Fr=500 N,轉速n=6 300 r/min,研究四點接觸球軸承各鋼球接觸角的變化。考慮到鋼球離心力和陀螺力矩的影響,正常工作狀態(tài)下的四點接觸球軸承鋼球與內外圈接觸角不再相等。本文得到的鋼球與內外圈接觸角結果如圖5所示,運轉過程中工作接觸角均大于墊片角,因此四點接觸球軸承不會出現多點接觸的現象,滿足設計要求。
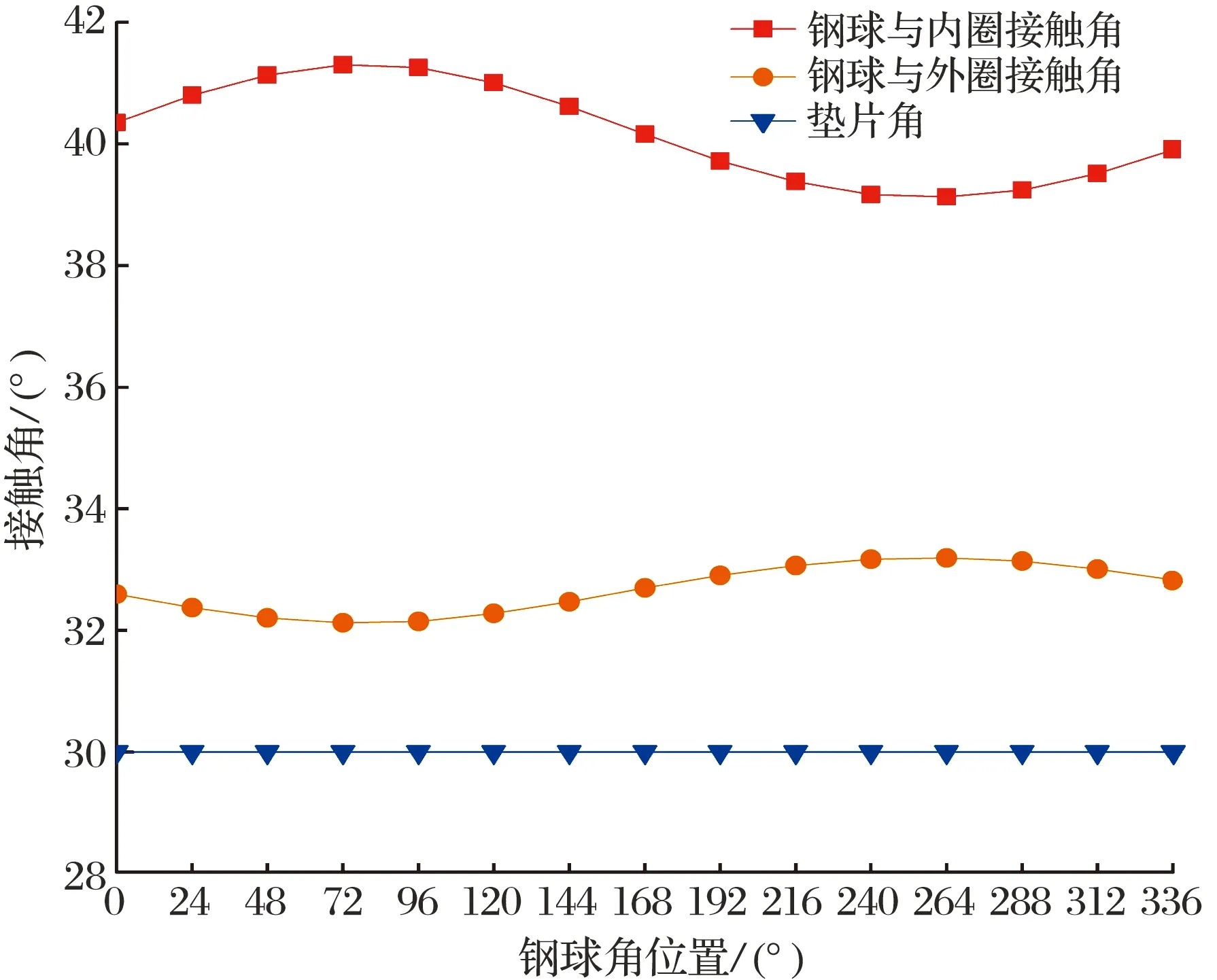
圖5 鋼球與內外圈接觸角
驗證優(yōu)化后軸承結構參數滿足設計要求后,對優(yōu)化前后目標函數值進行對比分析,結果見表2:優(yōu)化后四點接觸球軸承的額定動載荷增大了1.592%,摩擦力矩減小了4.051%,表明四點接觸球軸承的性能得到了進一步提高。
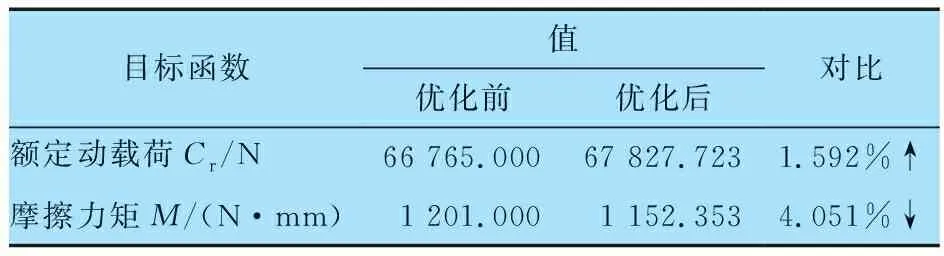
表2 優(yōu)化前后目標函數的對比結果
4 結束語
本文以傳動機構用四點接觸球軸承的額定動載荷和摩擦力矩為目標函數對軸承進行優(yōu)化,采用遺傳算法求解,并基于擬靜力學模型研究四點接觸球軸承的動態(tài)性能。優(yōu)化后的四點接觸球軸承在額定動載荷增大、摩擦力矩減小的基礎上,滿足運轉過程中任意角位置接觸角均大于墊片角的要求,防止四點接觸球軸承因多點接觸而失效的情況發(fā)生,為四點接觸球軸承的優(yōu)化設計提供了參考。

