聲學近零折射率材料的聲波調控研究

何 川, 張崇卓, 吳光華, 陶 猛

(貴州大學 機械工程學院, 貴陽 550025)

相比于傳統的共振型聲學超構材料,如薄膜型、亥姆霍茲型等,盤繞型聲學超構材料[11]具有結構穩定,低能量損耗的優點。盤繞型聲學超構材料可以讓聲波在有限的空間內盡可能地延長聲波地傳播路徑,增加波傳播時間,降低有效相速度,從而實現奇特的聲學現象。另一方面,受自然分形現象地影響,人們開始設計出具有自相似性結構的復合材料[12-13]。相比于傳統的機械結構設計,分形結構在超材料的設計中具有多尺度特性、自相似性、以及較高的空間利用率等特點。受分形結構在電磁超材料中的應用啟發,自相似技術在聲子晶體設計及性能分析中也得到了大量的關注。其中,Kuo等[14]通過試驗驗證了分形幾何結構可通過調節單胞內聲波散射長度來得到多重散射帶隙。Xu等[15]通過研究發現,二階分形的聲子晶體相比于常規的聲子晶體,前者更能夠獲得較寬帶隙。因此,如果將分形結構引入盤繞型聲學超材料中,利用自相似分形技術構建出基于空間盤繞形聲學超材料的多尺度自相似模型,將極大豐富盤繞型聲學超材料的設計手段,為寬頻帶的空間盤繞型聲學超材料的設計提供新的思路。

本文基于空間卷曲理念,利用分形自相似技術設計了一種聲學結構單元。通過周期性排列,構造了近零密度超材料,采用等效參數法分析了等效質量密度和體積模量的頻變特性。在近零密度頻率點處實現了聲隱身、聲隧穿、聲異常透射、波前整形。最后,通過試驗測試驗證了結構的有效性。

1 近零折射率單元模型及等效參數

如圖1(a)所示,該基本單元由兩個“Z”型通道首尾連接構成,選擇環氧樹脂作為構建單元結構的基體材料,其密度為ρ1=1 050 kg/m3,聲速2 500 m/s;該單元結構基本參數如表1所示,包括晶格常數a,方形實心框架的邊長d,通道寬度w,最小壁厚b。圖1(b)為仿真原理圖,背景介質為空氣,其密度ρ0=1.21 kg/m3,聲速c0=343 m/s,平面波從左入射,剛性薄壁可以近似為硬聲場邊界,故聲波在其內傳播時,只能沿著曲折聲通道進行傳播,曲折的次數越多,聲波傳播的路徑越長。采用等效參數提取法,通過數值計算該結構單元的透射系數與反射系數來反演該結構的等效聲學參數[16]。圖1(c)為該結構單元的等效質量密度以及等效體積模量倒數隨頻率的變化曲線。可以看出,在906 Hz附近,該結構單元的等效質量密度ρeff和等效體積模量的倒數1/βeff同時趨近于0,表明該結構單元在906 Hz附近其等效折射率趨近于零。

(a) 單胞模型

(b) 仿真原理圖

(c) 單元等效質量密度曲線及其等效體積模量的倒數曲線圖1 近零折射率單元模型及其等效參數Fig.1 Near-zero refractive index element model and its equivalent parameter diagram

表1 基本單元結構參數Tab.1 Parameters of basic unit structural

2 近零折射率聲超構材料的應用

近零折射率結構單元經過合理的周期性排布之后可以實現聲隱身、聲隧穿等特殊聲學現象。由于多個結構單元間會產生共振耦合作用,從而導致單個結構單元的近零密度點的選取不再適用于周期性排列結構,此時采用一種評價均勻和各向同性材料的聲學特性方法:傳遞矩陣法[17],來對周期性排列結構的等效質量密度進行分析計算。

2.1 聲隱身

通過構造如圖2(a)所示的模型來考察該近零折射率聲超構材料的聲隱身效應。圖2(a)中彩色部分為近零折射率聲超構材料,其內部放置了四個尺寸為200 mm×200 mm的剛性散射體,將該模型放置于矩形波導中,平面波從左入射。圖2(a)給出了該聲隱身斗篷的聲壓場云圖,可以看出,經過近零折射率聲超材料包裹后的剛性散射體很好的得到了隱藏。這是因為近零折射率材料對于聲波的傳播具有方向選擇性,聲波從左入射進入近零折射率材料后,由于近零折射率材料的引導,聲波繞過了剛性散射體從右邊出射。可以看到,聲波經過超材料包裹后的剛性散射體后其出射波形仍然能夠保持很好。作為對比,當入射平面波經過無近零折射率聲超構材料包裹后的剛性散射體時,其出射波形發生了明顯的紊亂,其原因在于平面聲波入射后受到了四個剛性散射體的大量反射。圖2(b)給出了該聲隱身模型的透射系數以及近零密度曲線,可以看到該結構模型在514 Hz附近處于近零密度點,其透射率接近于1,聲波在該頻率點處實現了全透射,聲能量沒有出現損耗。

(a) 聲隱身斗篷模型及其聲壓場分布圖

(b) 514 Hz附近的透射系數及其等效質量密度曲線圖2 近零折射率材料制成的聲隱身斗篷Fig.2 Acoustic invisibility cloak made of near-zero refractive index material

2.2 聲隧穿

為了說明近零折射率結構不僅在平直波導中具有聲波調控作用,而且在狹窄區域、彎曲波導中同樣具有調控作用,構造了如圖3(a)所示的“Z”型波導。其中彩色部分為近零折射率聲超構材料填充的波導部分,近零密度頻率平面聲波從左入射。圖3(a)還給出了平面波經過近零折射率聲超構材料填充的“Z”型波導后的聲壓場分布云圖,可以看出,平面波經過近零折射率材料填充的波導后,其出射波形仍然保持良好。作為對比,當平面波經過去除近零折射率聲超構材料填充的波導后,其出射波波陣面出現了紊亂,且入射波陣面也出現了紊亂現象,這主要是因為平面波在“Z”型波導的拐角處產生了大量反射,進而變得散亂。圖3(b)給出了該結構模型的透射系數曲線以及近零密度曲線,可以看出,在3 171.3 Hz附近,該近零折射率聲超構材料處于近零密度頻率點,在該頻率點處,其透射系數接近于1,聲波在該頻率點實現了全透射,沒有聲能量的損耗。因此,可以得出結論:在該頻率點處,平面聲波經過由該近零折射率聲超構材料填充的波導后可以產生聲波隧穿效應。

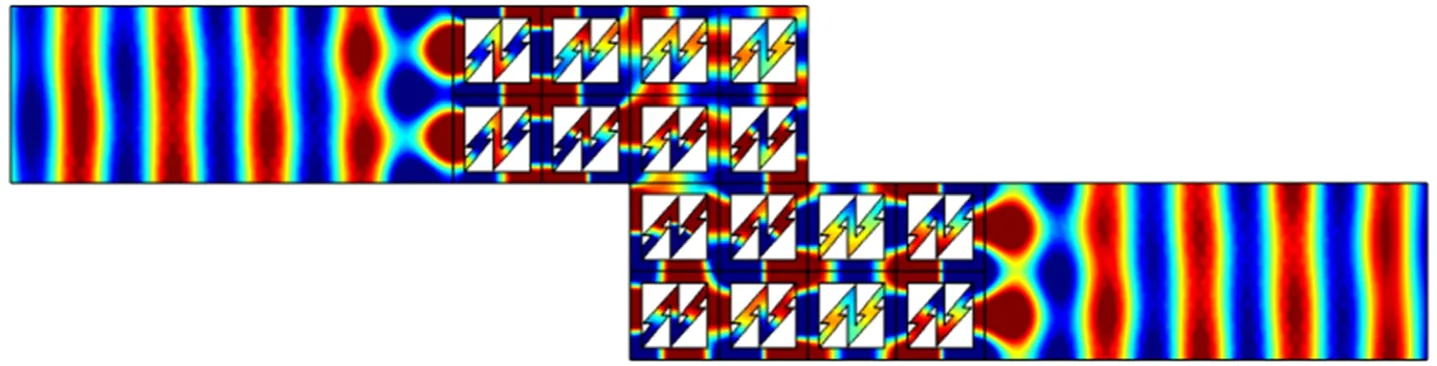
(a) 聲隧穿模型及其聲壓場分布圖

(b) 3 171.3 Hz附近的透射系數及等效質量密度曲線圖3 近零密度材料的聲隧穿效應Fig.3 Acoustic tunneling effect of near-zero density transmission

2.3 聲異常透射

如圖4(a)所示,灰色區域為兩剛性散射體,彩色部分為近零折射率聲超構材料填充的波導部分,空氣中的兩剛性散射體中間存在一條水平狹縫,近零密度頻率聲波從左入射。實現聲異常透射的物理機理在于近零折射率聲超構材料對于聲波的傳播具有方向選擇性,當聲波從左垂直入射進入近零折射率聲超構材料,由于水平狹縫與左端近零折射率材料出射面垂直,因此平面聲波在經過近零折射率材料后產生隧穿效應,聲波繞過剛性散射體進入到右端狹縫之中。聲波在狹縫中水平傳播,水平狹縫與右側近零折射率聲超構材料垂直,聲波進入右側近零折射率聲超構材料,由于出射波與右側近零折射率聲超構材料出射面垂直,故出射波仍為平面波,從而實現聲異常透射。

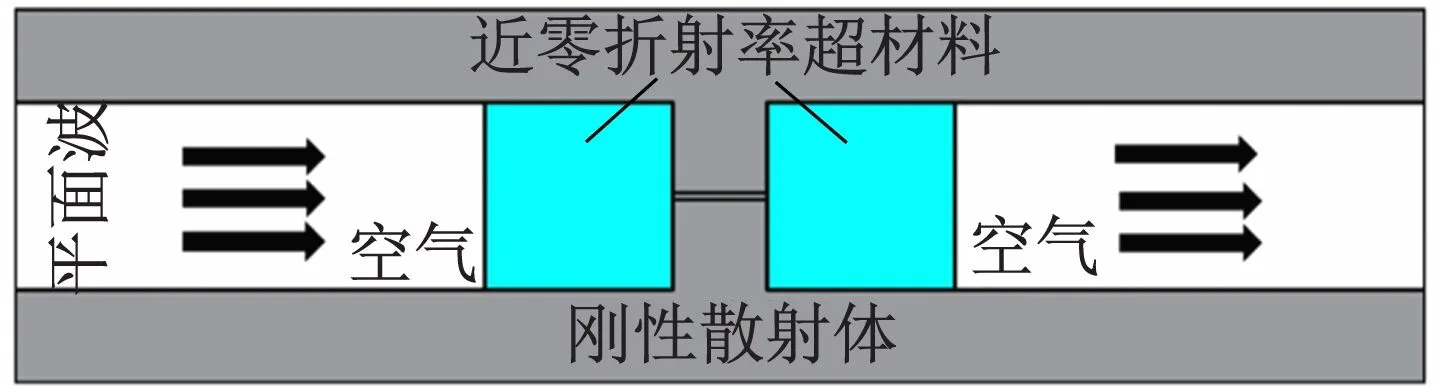
(a) 聲異常透射模型及其聲壓場分布圖

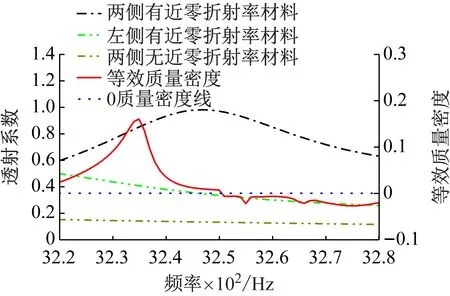
(b) 3 250.2 Hz附近的透射系數及其等效質量密度曲線圖4 近零折射率材料的聲異常透射Fig.4 Abnormal sound transmission of near-zero refractive index materials

為驗證該方案的可行性,圖4(a)分別給出了聲波經過三種情況下的聲壓場分布云圖。可以看出,當狹縫兩端都置有近零折射率聲超構材料時,平面波出射后,其波陣面仍然保持良好,能量透射率也較高。作為對比,圖4(a)還給出了只有狹縫左側置有近零折射率聲超構材料和左右兩側均沒有放置近零折射率聲超構材料的聲壓場分布云圖。可以看出,后兩者出射波形均出現了不同程度的紊亂,且聲能量透射率依次降低,為更直觀的看出三種情況下透射聲能量的情況,圖4(b)給出了三種情況下的透射系數曲線以及該近零折射率聲超構材料的等效質量密度曲線。可以看出,在近零密度頻率點3 250.2 Hz處,狹縫兩端置有近零折射率聲超構材料的聲波透射系數接近于1,聲波實現了全透射,沒有聲能量的損耗,而后兩者相比之下其聲能量透射率要低的多,其中狹縫兩端均無近零折射率材料的情況下透射率最低,其主要原因在于聲波從左側入射后受到了上下兩剛性散射體的大量反射,使得僅有部分聲波透過狹縫。

2.4 波前整形

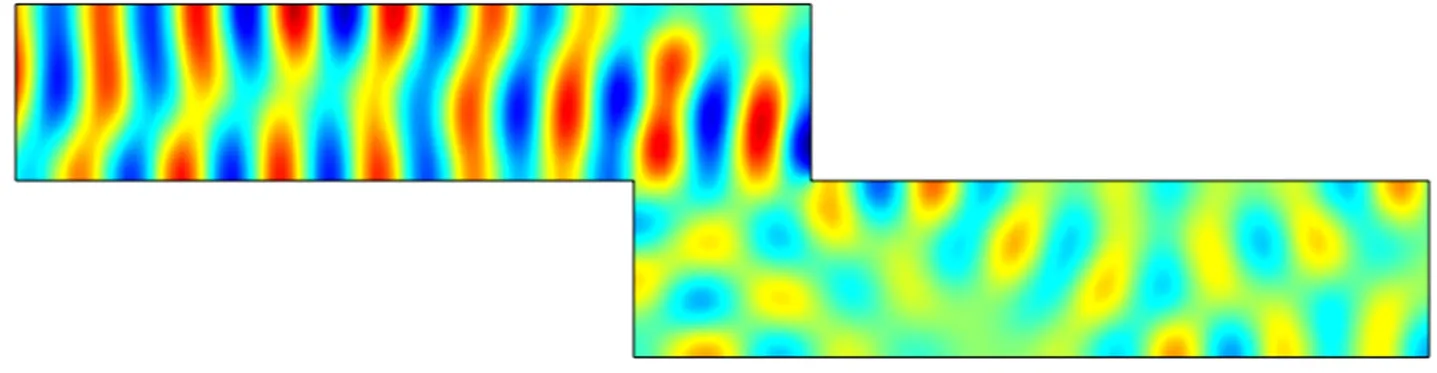
通過在矩形波導前面放置兩個大小不一的橢圓形剛性散射體來模擬不均勻的散射聲場,以此來研究該近零折射率聲超構材料對散射聲場的整形作用,如圖5(a)所示。圖5(a)還給出了在波導中不放置2×3的周期性結構,近零密度頻率的平面聲波經過后的聲場分布,可以看出,聲波經過兩橢圓形剛性散射體后,入射平面波受到了擾亂,在經過一段距離的傳輸后,仍然未恢復原本的平面波波陣面。作為對比,在矩形波導中放入2×3的周期性結構后,出射波波陣面不再出現紊亂,重新恢復到了原本的平面波波陣面,可以證明在近零密度頻率點處,該周期性結構具有平整紊亂聲波的作用。圖5(b)給出了平面聲波經過該周期性結構后的透射系數圖以及它的等效質量密度曲線,可以看出,該周期性結構在2 088 Hz附近處于近零密度頻率,透射系數峰值為0.85,透射系數幅值的降低其原因主要歸因于平面聲波從左入射后受到兩橢圓形剛性散射體的反射作用,使得僅有部分聲波進入近零折射率聲超構材料的左側表面。

(a) 波前整形模型及波前整形聲壓場分布

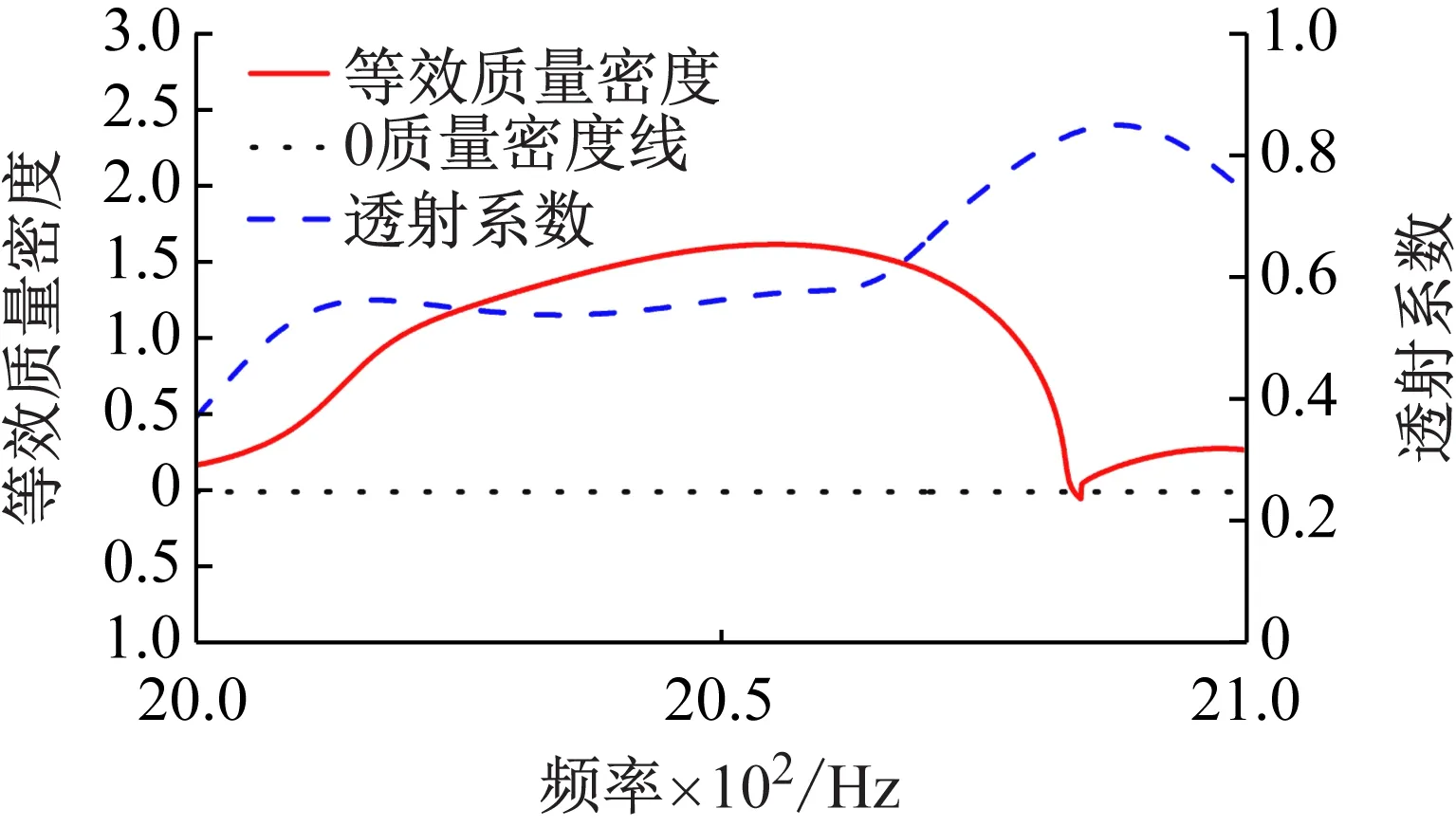
(b) 2 088 Hz附近的透射系數及等效質量密度曲線圖5 近零折射率材料的波前整形效應Fig.5 Wavefront shaping effect of near-zero refractive index materials

3 試驗驗證

如圖6(a)所示,為了驗證文章中有限元分析方法的有效性,采用環氧樹脂材料對該單元結構進行了3 d打印,底部結構采用74.5 mm×74.5 mm×2 mm的基底板起固定支撐作用。考慮到樣品表面并非絕對光滑表面,存在一定的黏滯摩擦,因此在進行仿真分析時采用壓力聲學-熱黏性模塊。圖6(b)為用于試驗的阻抗管測試系統,內部截面尺寸為100 mm×100 mm。圖6(c)為透射系數的數值計算結果與試驗結果的對比。從圖中可以看出,試驗與仿真結果的透射系數曲線存在幅值上的偏差和峰值頻率的偏差,仿真中的峰值所在的頻率為910 Hz,試驗測試中的峰值頻率為1 046 Hz,產生了136 Hz的偏差,經過多次試驗測量,峰值頻率產生偏差的原因可以歸結為以下幾點:① 由于在打印樣品時其樣品模型需要底部基底的支撐,基底板的存在阻止了部分聲波的傳播,在本試驗樣品中,樣品基底板厚度為2 mm;② 3D打印樣品其聲通道存在一定的誤差。其次,需要注意的是,試驗透射系數曲線在1 340 Hz附近與仿真結果存在出入,其原因可以歸因于試驗過程中存在外界噪聲的影響,且實際過程中,聲波與阻抗管壁的摩擦更為劇烈。導致更多的聲能量損耗。盡管仿真與試驗結果存在一定的偏差,但是其透射系數整體趨勢仍然可以得到很好的證明,說明了前文計算結果的準確性。

(a) 試驗樣品

(b) 阻抗管試驗裝置,1-信號發生器,2-功率放大器,3-計算機,4-阻抗管

(c) 試驗與仿真結果對比圖圖6 試驗模型及其聲學特性Fig.6 Test model and its acoustic characteristics

4 結 論

本文基于盤繞型聲學超構材料,利用分形自相似技術設計了一種近零折射率結構單元,采用等效參數

法計算了該結構單元的等效聲學參數。并以該近零折射率結構單元為基礎,通過合理周期性排布之后,在其各自的近零密度頻率點附近,由該基本單元構成的聲學超構材料可以實現特殊聲學現象,如聲隱身、聲隧穿、聲異常透射、波前整形。同時對該近零折射率結構單元的透射系數進行了試驗測試,實測透射系數與仿真結果符合較好,驗證了模型的有效性和計算結果的準確性,表明本文設計的近零折射率聲超構材料在聲隱身、彎曲波導等方面具有潛在應用價值。