基于參數自尋優變分模態分解的信號降噪方法
何成兵, 車其祥, 徐振華, 于慶彬, 董玉亮, 程睿翔
(1.華北電力大學 能源動力與機械工程學院,北京 102206;2.國網福建省電力公司電力科學研究院,福州 350007;3.國網山東省電力公司電力科學研究院,濟南 250000)
滾動軸承在各類旋轉機械設備中應用廣泛,同時也是設備中最易損壞部件之一。統計數據表明,在使用滾動軸承的旋轉機械中,約30%的機械故障是由滾動軸承引起的。滾動軸承振動信號具有沖擊性、非線性、非平穩的特性,信號微弱、調制性強,而且由于旋轉機械設備運行工況復雜,背景噪聲污染嚴重,導致滾動軸承故障信號常常淹沒于噪聲之中[1]。因此,對滾動軸承故障信號進行降噪處理,獲得有效故障特征,對于后續的故障信號分析與故障診斷具有重要的意義。
目前常用的降噪方法有小波變換(wavelet transform, WT)、經驗模態分解(empirical mode decomposition, EMD)、集合經驗模態分解(ensemble empirical mode decomposition, EEMD)以及變分模態分解(variational mode decomposition, VMD)等。WT在信號降噪處理時的缺點是小波基函數和小波閾值函數的選擇不具有唯一性,受主觀性影響較大,很難保證降噪效果最優。為克服WT的缺點,曹玲玲等[2]結合快速譜峭度和帶通濾波以及Hilbert包絡分析,提出了一種新的改進小波閾值函數進行信號降噪;Malla等[3]利用復Morlet小波分析,得到滾動軸承故障的相位圖和振幅圖,有效提取出了軸承故障特征。
EMD方法在信號分解過程中存在模態混疊、端點效應及產生虛假分量等缺陷,使得信號中特征頻率與噪聲的分離程度不足[4]。EEMD對EMD進行了優化改進,李思琦等[5]利用EEMD對信號進行分解,提出了一種基于EEMD與卷積神經網絡相結合的滾動軸承故障診斷方法;Yin等[6]利用改進EEMD將原始信號中隱藏的固有噪聲分離,提出了一種基于改進EEMD和自適應閾值去噪的滾動軸承弱故障特征提取新方法。EEMD可以在一定程度上抑制模態混疊現象,但也存在計算量大、頻譜剖分效果不理想的缺點。
VMD是一種新的非遞歸信號分解方法,它克服了EMD等算法存在的模態混疊和頻率效應等缺點,具有很好的噪聲魯棒性和降噪效果,得到了廣泛應有。Wang等[7]采用VMD進行碰摩信號的等效濾波特性分析,并與EWT、EMD和EEMD方法進行了比較,證明VMD在提取瞬態沖擊方面更有效;朵慕社等[8-10]提出一種基于改進VMD降噪和卷積神經網絡的軸承故障智能診斷方法,其VMD分解層數通過排列熵閾值法確定,結合峭度準則和互相關準則,進行IMF分量選取與信號重構,取得了較為理想的降噪效果。
在利用VMD進行信號降噪處理時,需提前設定模態數K和二次懲罰因子α等參數,由于K和α的取值對降噪效果有很大的影響,它需要自適應獲得最佳值,而不是人為主觀設定。目前主要采用以下三種途徑來獲得K和α的優化參數[11]:一是根據先驗知識或中心頻率觀察法選取,如Qiao等[12]對原始信號進行VMD分解時,根據每個IMF分量的中心頻率確定K值,這種方法適應性較差,且不能保證VMD分解精度;二是通過評價指標來選取,如Zhang等[13]通過能量和相關系數確定K值,這種方法選取的K值并不適用于所有的信號;三是采用元啟發式算法進行參數自適應尋優,如人工魚群算法(artificial fish swarm, AFS)[14]、灰狼算法(grey wolf, GW)[15]、蚱蜢算法(grasshopper optimization, GO)[16]、鯨魚算法(whale optimization, WO)[17]、蝙蝠算法(bat optimization, BO)[18]和粒子群算法(particle swarm optimization, PSO)[19]等,這些優化算法可搜尋到優化參數,但一般需要大量的迭代計算,同時,由于各實際應有領域的信號與噪聲特點不同,這些算法在應用于具體領域時,如何設定恰當的適應度函數、如何提高算法搜索能力以及避免陷入局部最優解,是急需解決的問題。
針對上述問題,本文提出了一種基于參數自尋優變分模態分解的信號降噪方法。首先提出了一種改進粒子群算法(improved particle swarm optimization, IPSO),以實現VMD最優模態數K和二次懲罰因子α的自適應尋優,該算法結合滾動軸承故障信號特點,建立了模態復合熵新指標,并以之作為適應度函數,同時設計了慣性權重值隨搜索進程先大后小的計算公式、邊界粒子以及粒子群優化處理原則,既提高了IPSO算法搜索能力,又避免了算法早熟收斂、陷入局部最優解;然后基于最優K和α,對原始信號進行VMD分解,獲得K個IMF分量;利用相關系數篩選法,進行IMF分量的有效模態和含噪模態識別,并利用小波閾值去噪方法對含噪模態進行去噪處理;最后將有效模態與去噪后的含噪模態進行重構,實現信號降噪。數值仿真和試驗數據分析表明本文所提方法降噪效果明顯,有利于滾動軸承故障特征的提取。
1 相關理論基礎
1.1 VMD算法
VMD將一個時域信號f(t)分解為K個具有調頻-調幅特性和稀疏特性的本征模態函數uk(t)
uk(t)=Ak(t)cos(φk(t))
(1)
各IMF中心頻率為ωk(t),為使每個模態的估計帶寬之和最小,建立如下約束變分模型
(2)
為求取式(2)最優解,引入擴展Lagrange函數,將約束性變分問題變換為非約束性變分問題,其表達式為
(3)
式中,α為二次懲罰因子,用于保證信號的重構精度,α值越大,各模態分量的頻率帶寬就越小。
利用交替方向乘子算法求取式(3)的鞍點,即求取約束變分模型的最優解,其中模態分量uk及中心頻率ωk分別為
(4)
(5)
VMD算法實現過程如下:
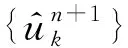
(6)
步驟4 重復步驟2、步驟3,直到滿足式(7)所示的迭代停止條件,結束循環,得到K個變分模態分量。
(7)
式中,ε為求解精度。
1.2 PSO算法
PSO算法模擬鳥群的捕食行為,將每只鳥視為粒子,作為基本運算單位,其優化問題的實質是通過粒子的運動方向和速度確定最優解在空間中的位置。其基本原理為:設搜索域為D維,共有m個粒子構成群體,第i個粒子位置表示為向量xi=(xi1,xi2,…,xiD),飛行速度表示為向量vi=(vi1,vi2,…,viD),xi位置變化就是解的軌跡,用適應度函數Q(xi)來權衡粒子位置的好壞。第i個粒子所經歷的個體最優位置記為pi=(pi1,pi2,…,piD) ,搜索域中整個粒子群全局最優位置記為pg=(pg1,pg2,…,pgD)。各粒子的速度和位置通過下式更新
vid(k+1)=ωvid(k)+c1r1(pid(k)-xid(k))+
c2r2(pgd(k)-xid(k))
(8)
xid(k+1)=xid(k)+vid(k+1)
(9)
式中:k為粒子群迭代次數;i=[1,m]為粒子數;d=[1,D]為空間維數;r1和r2為相互獨立的0~1之間的隨機數;c1和c2分別為粒子向個體和全局最優位置方向的學習因子;vid(k)和xid(k)分別為第i個粒子在d維空間內k次迭代的速度和位置;pid(k)和pgd(k)分別為第i個粒子在d維空間內k次迭代的個體和全局最優位置;ω為慣性權重。
PSO算法實現過程如下:
步驟1 算法初始化,設定粒子群的維度D、群體規模m、最大迭代次數Np、粒子位置范圍、速度范圍。
步驟2 計算每個粒子的適應度函數值,確定粒子個體最優位置pi=(pi1,pi2,…,piD)和粒子群全局最優位置pg=(pg1,pg2,…,pgD)。
步驟3 根據式(8)、式(9)更新調整粒子的速度和位置。
步驟4 迭代終止條件一般選為最大迭代次數Np或粒子群最優位置小于設定的最小閾值,判斷是否滿足迭代終止條件,不滿足則轉到步驟2,滿足則結束。
1.3 小波閾值去噪算法
小波閾值去噪是建立在小波變換基礎上的算法,其基本原理為:對含噪信號進行小波變換,根據信號具有真實信號通常為低頻、噪聲信號多為高頻的特點,對各頻帶小波系數與小波閾值進行比較,甄別出有效信號與噪聲信號,并通過小波重構得到去噪信號。
小波閾值去噪算法實現過程如下:
步驟1 設定小波分解層數,選定小波基函數,構造小波閾值函數。
步驟2 使用選定的小波基函數對含噪信號進行Mallat算法處理,得到分解層數對應的小波高頻系數和低頻系數;
步驟3 將小波系數與小波閾值進行比較,如果小波系數大于小波閾值,對應數據為有效信號,則該小波系數保留;反之,為噪聲信號,該小波系數舍棄。
步驟4 對保留的小波系數重構,得到去噪信號。
2 改進粒子群算法(IPSO)
本文提出了一種改進粒子群算法(improved particle swarm optimization,IPSO)進行VMD參數自適應尋優,以確定VMD最優的K和α。該算法的特點在于:從滾動軸承故障信號特點出發,提出了模態復合熵新指標,并以之作為適應度函數;設計了慣性權重值隨搜索進程先大后小的計算公式、邊界粒子以及粒子群優化處理原則,提高了IPSO算法搜索能力,也避免了算法早熟收斂、陷入局部最優解。
IPSO算法流程如圖1所示,具體實現過程如下:
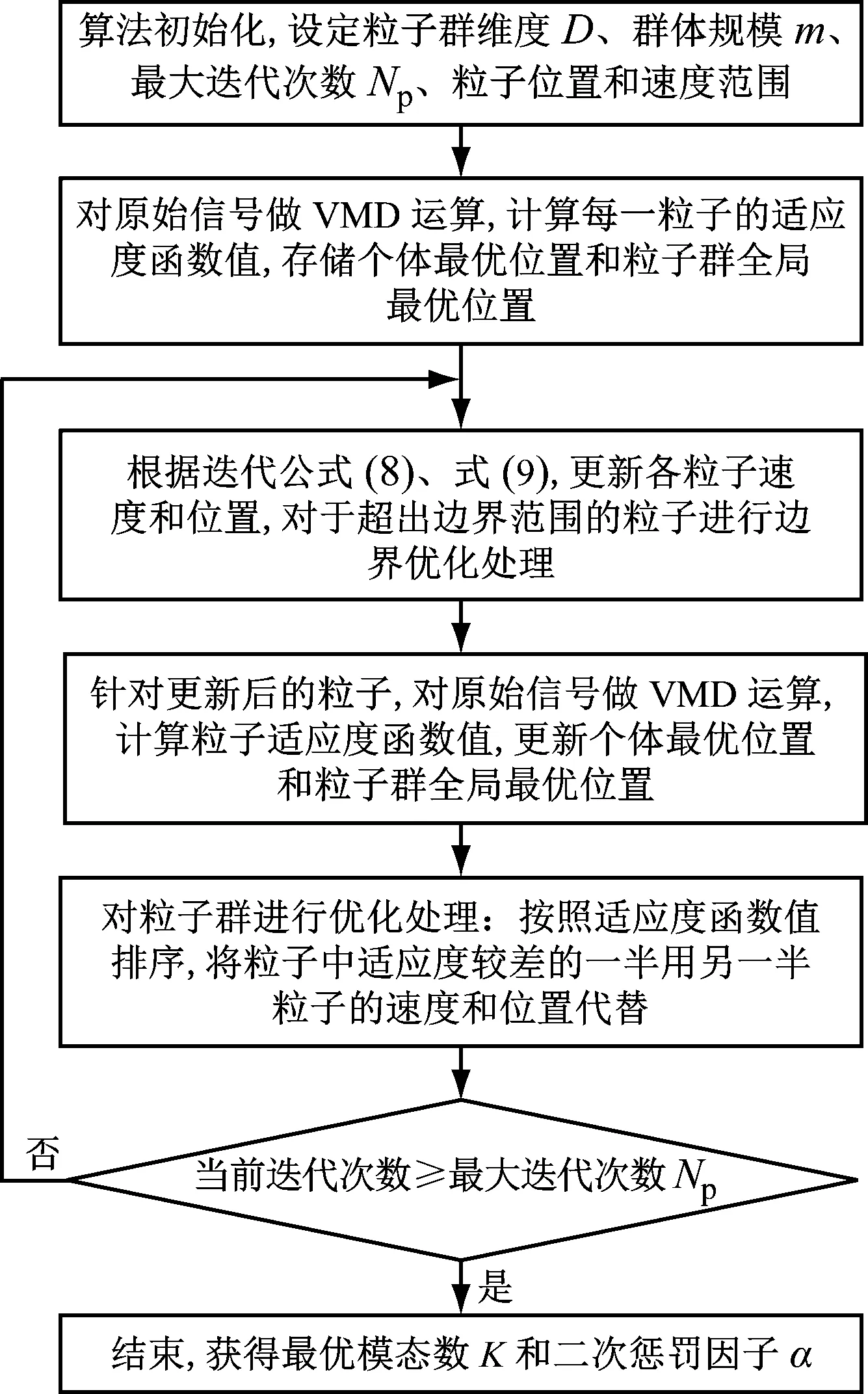
圖1 IPSO流程圖Fig.1 The flow diagram of IPSO
步驟1 算法初始化。設定粒子群維度數D為 2,對應VMD的模態數K和二次懲罰因子α;在2維可行域中隨機選取m個粒子,對粒子位置、飛行速度隨機初始化;第i個粒子在2維空間的位置表示為向量xi=(xi1,xi2),飛行速度表示為向量vi=(vi1,vi2)。
步驟2 針對某一粒子的2維位置組合,對原始信號做VMD運算,得到K個模態分量{uk},計算每一粒子的適應度函數值Q(uki(1)),對各粒子進行評價,選取適應度函數值最小者為最優,存儲對應粒子的個體最優位置pi=(pi1,pi2) 以及整個粒子群全局最優位置pg=(pg1,pg2)。
通過對{uk}分析發現:如果{uk}中包含噪聲越多,則信號復雜性越高,對應的模態復合熵越大,反之,則模態復合熵越小。因此,以{uk}的模態復合熵Ec作為適應度函數Q(uk),且以模態復合熵最小作為適應值,適應度函數如式(10)所示
Q(uk)=Ec=β1·Eenergy+β2·Eenvelope
(10)
式中:Eenergy為模態能量熵;Eenvelope為模態包絡熵;β1,β2為二者的權重系數,β1+β2=1,對于如滾動軸承故障這樣具有明顯沖擊特征的信號,取β1<β2,否則取β1≥β2。
模態能量熵Eenergy的計算式如下
(11)
模態包絡熵Eenvelope的計算式如下
(12)
式中,H為信號uk的Hilbert變換。
步驟3 根據迭代公式(8)更新各粒子速度,根據式(9)更新各粒子位置。
式(8)中慣性權重ω對算法搜索結果影響較大,其取值大則種群粒子搜索能力強,可探索較大的區域,取值小則可精細搜索目標,局部搜索能力強。為提高算法搜索能力,同時避免陷入局部最優解,采用ω權重值隨搜索進程先大后小的原則動態設定
(13)
式中:ωmax,ωmin為慣性權重的最大值和最小值,取ωmax=0.9,ωmin=0.4;t為粒子迭代次數;Np為最大迭代次數;Dec為衰減因子,其值為小于1的正數。
粒子位置更新后,有可能出現粒子的某一維度超出設定范圍的情況,此時粒子容易在邊界附近聚集,導致算法早熟收斂。因此,對超出邊界范圍的粒子進行邊界優化處理:將該維度的位置值設置為邊界值;該維度的速度乘以0~1之間的隨機數,并將其方向設為反方向,以此緩解因粒子在邊界聚集而引起的算法早熟收斂。計算公式如下
(14)
式中:xid,vid是第i個粒子第d維的位置和速度;xmaxd,xmind是粒子第d維的上限和下限值。
步驟4 針對位置更新后的粒子,對原始信號做VMD運算,計算每一粒子新的適應度函數值Q(uki(k+1)),并更新粒子個體最優位置pi(k+1)及粒子群全局最優位置pg(k+1)。粒子i的個體最優位置更新公式如下
pi(k+1)=
(15)
粒子群全局最優位置更新公式如下
(16)
步驟5 為提升算法性能,提高算法收斂速度,對粒子群進行優化處理:按照適應度函數值對所有粒子進行排序,并將粒子中適應度較差的一半用另一半粒子的速度和位置代替,但不改變原有粒子的個體最優位置pi(k+1)和粒子群全局最優位置pg(k+1)。
步驟6 判斷當前迭代次數是否達到最大迭代次數Np,如果未達到,返回步驟3進行下一次迭代;如果已達到,則迭代終止,輸出最優粒子2維位置,即獲得最優模態數K和二次懲罰因子α。
3 本文所提降噪方法流程
本文提出的基于參數自尋優變分模態分解與小波閾值處理的信號降噪方法流程如圖2所示,具體實現步驟為:
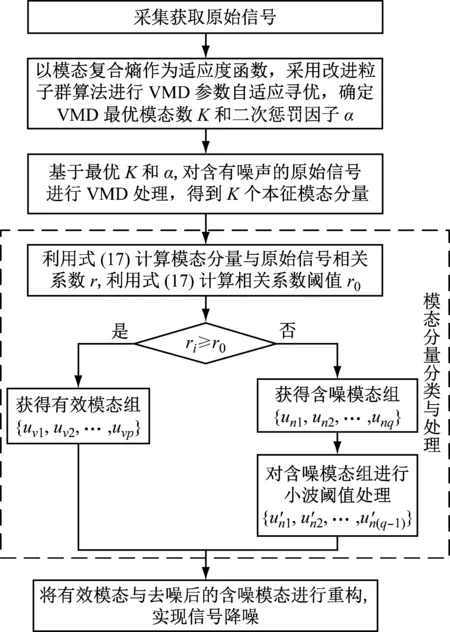
圖2 本文降噪方法流程圖Fig.2 The flow diagram of signal denoising method in this paper
步驟1:采集獲取原始信號x(t);
步驟2:以模態復合熵作為適應度函數,采用IPSO算法進行VMD參數自適應尋優,確定VMD最優模態數K和二次懲罰因子α;
步驟3:基于最優模態數K和二次懲罰因子α,對含有噪聲的原始信號進行VMD處理,得到K個本征模態分量{uk};
步驟4:利用相關系數篩選法,進行模態分量{uk}的有效模態和含噪模態分類,利用小波閾值去噪方法對含噪模態進行去噪處理。具體流程如下:
(1) 利用式(17)計算各模態分量{uk}與原始信號x(t)之間的相關系數r,相關系數越大,表示兩信號之間的關聯性越強
(17)
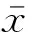
利用下式計算相關系數閾值r0
(18)
式中,rmax為各模態分量相關系數最大值。
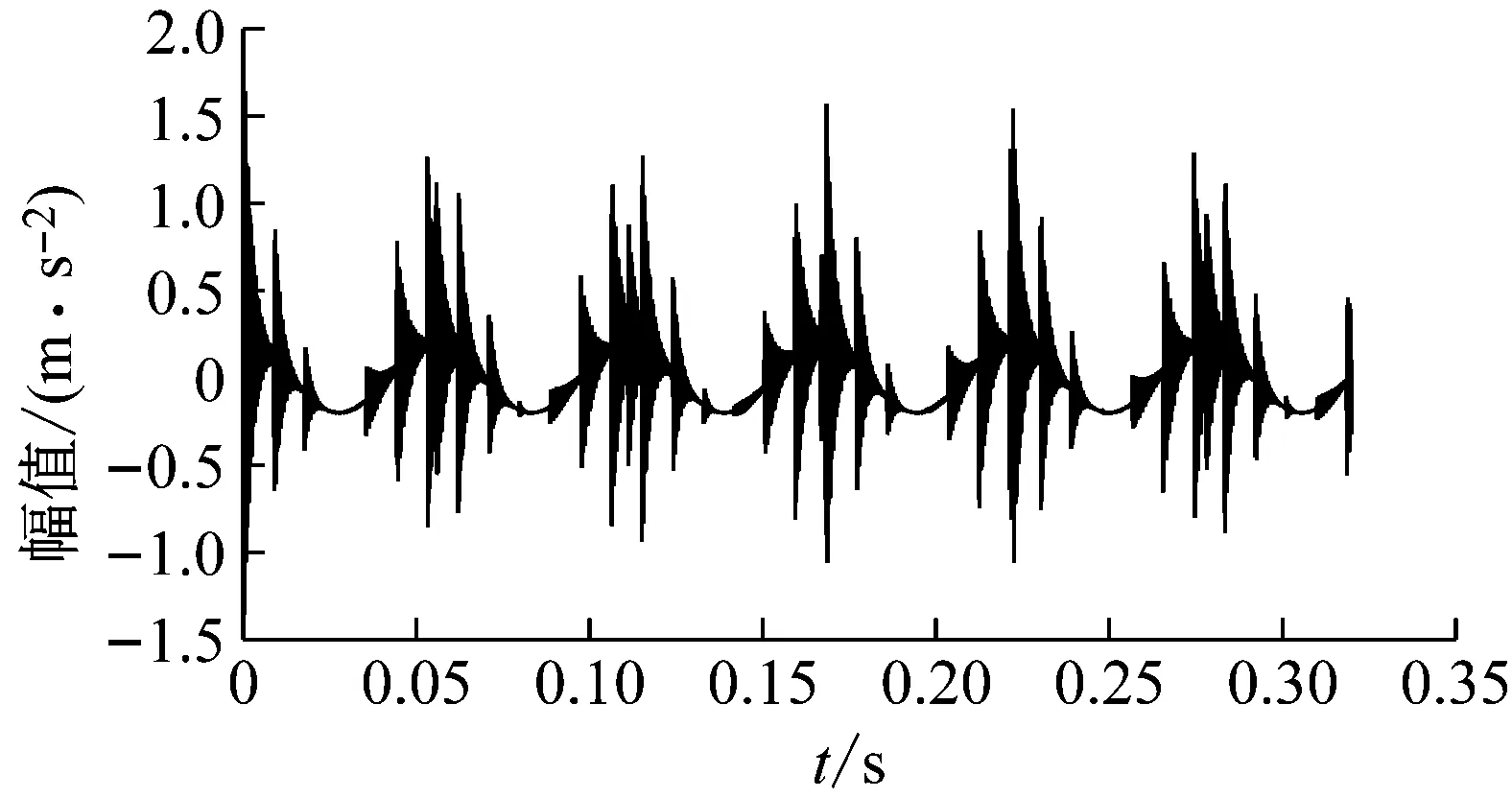
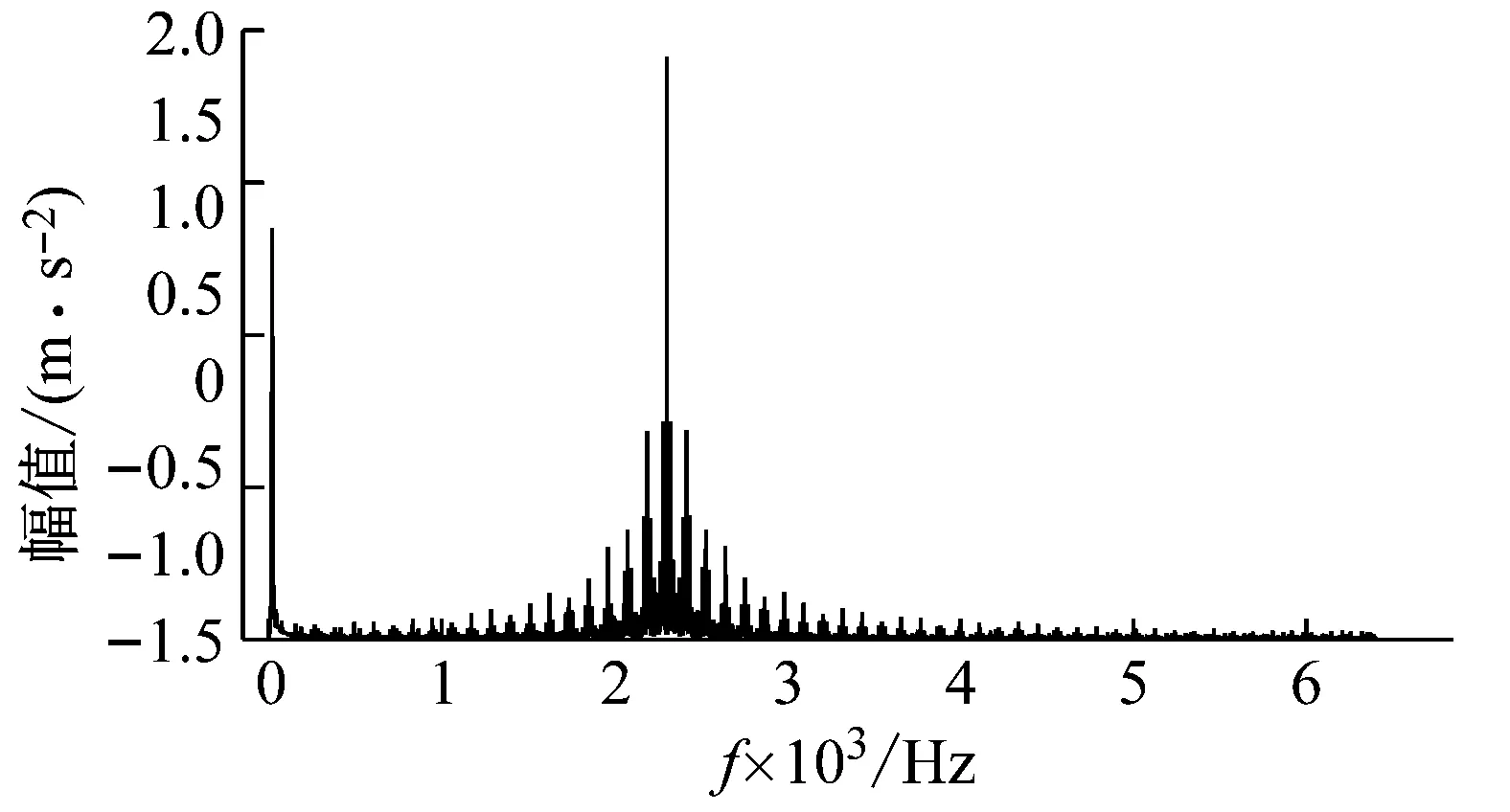
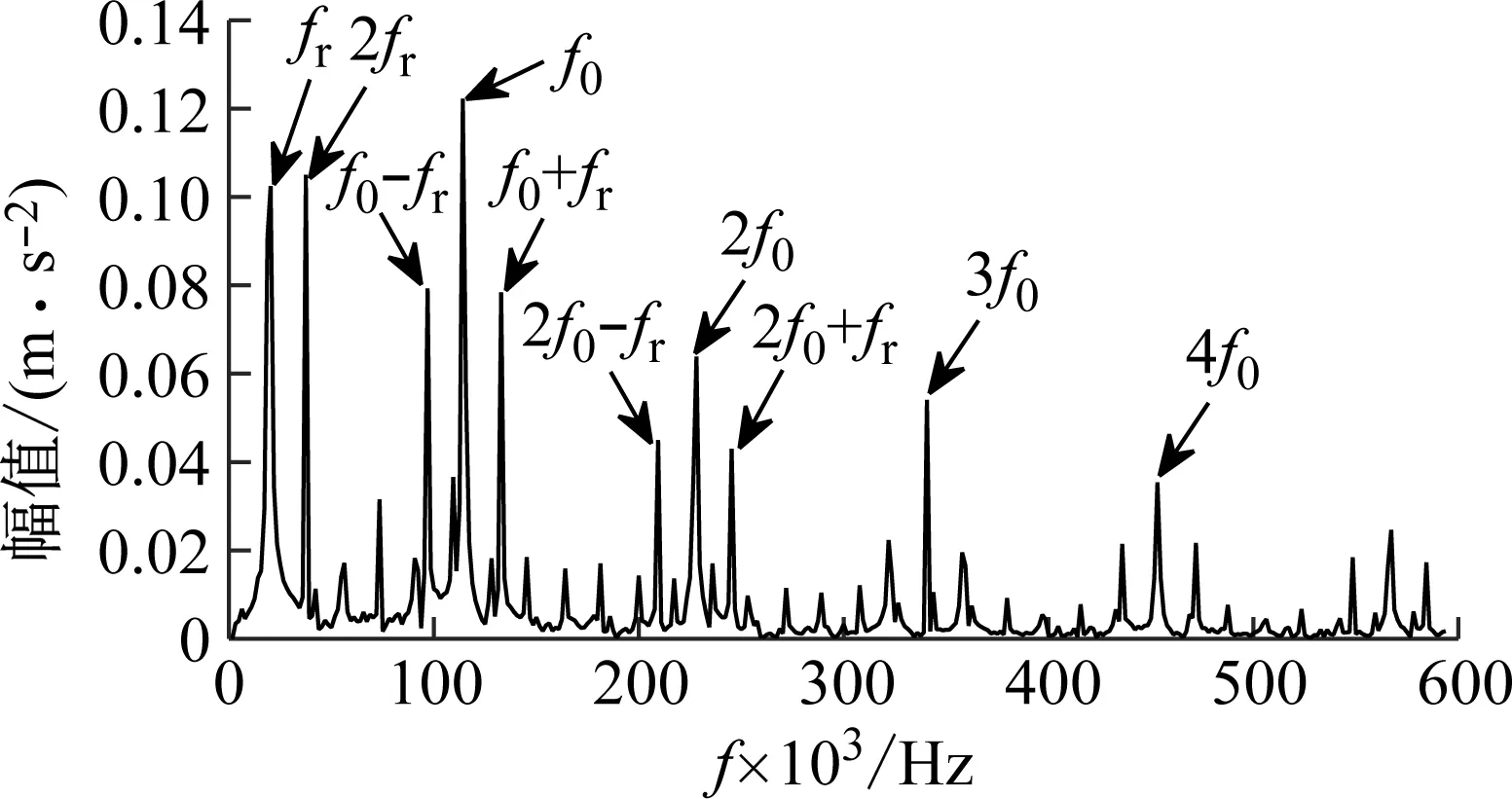
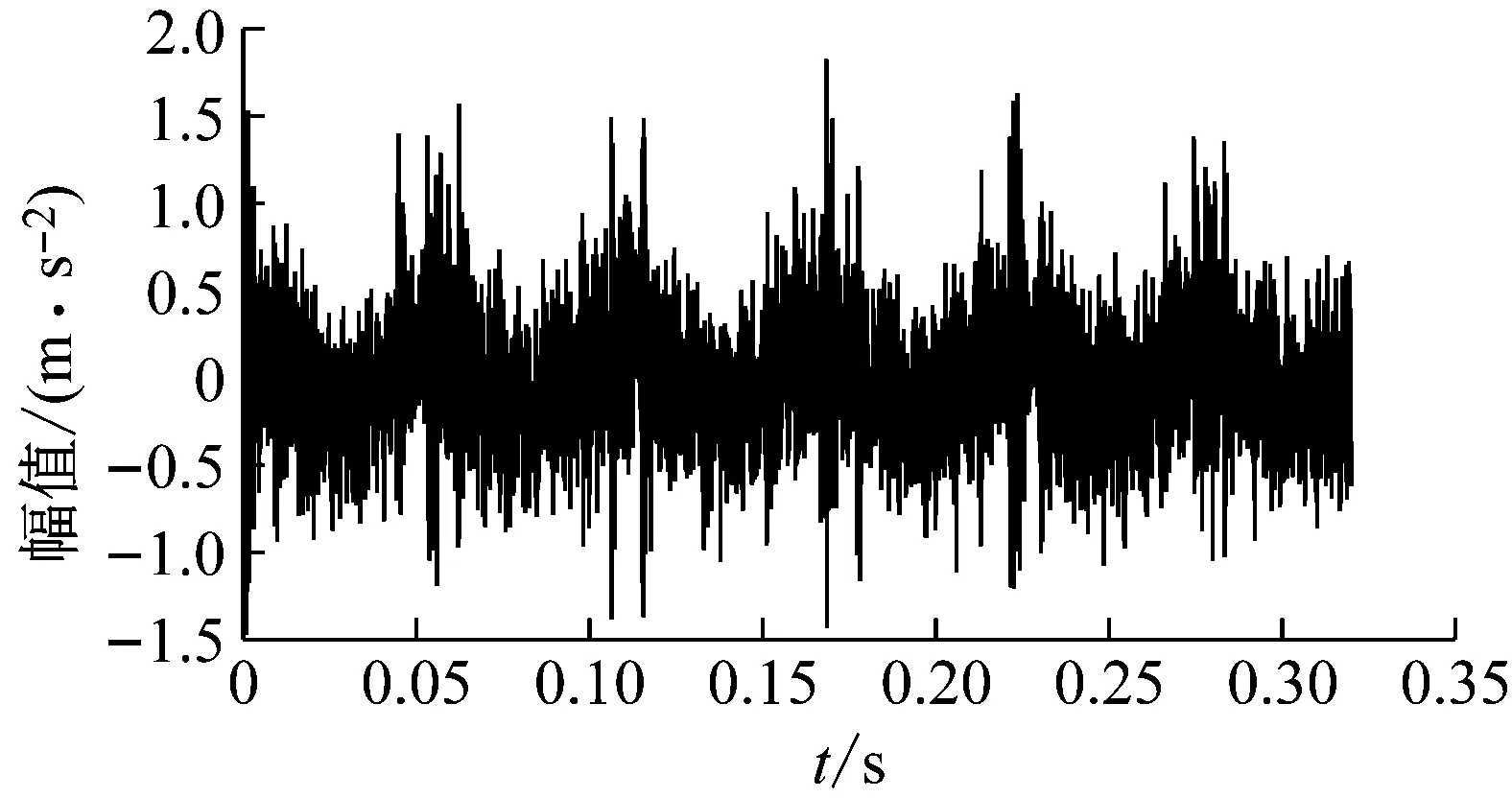
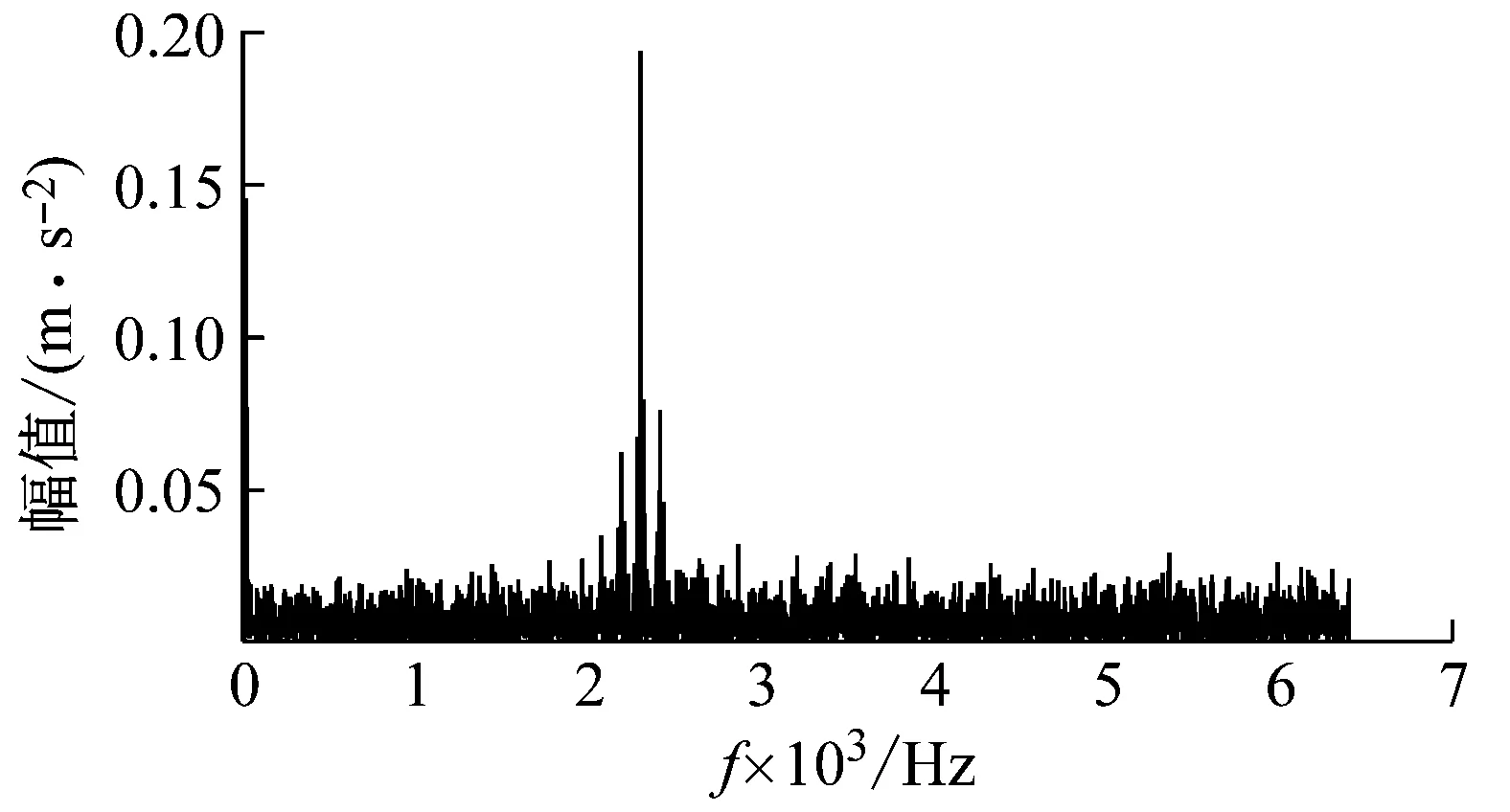
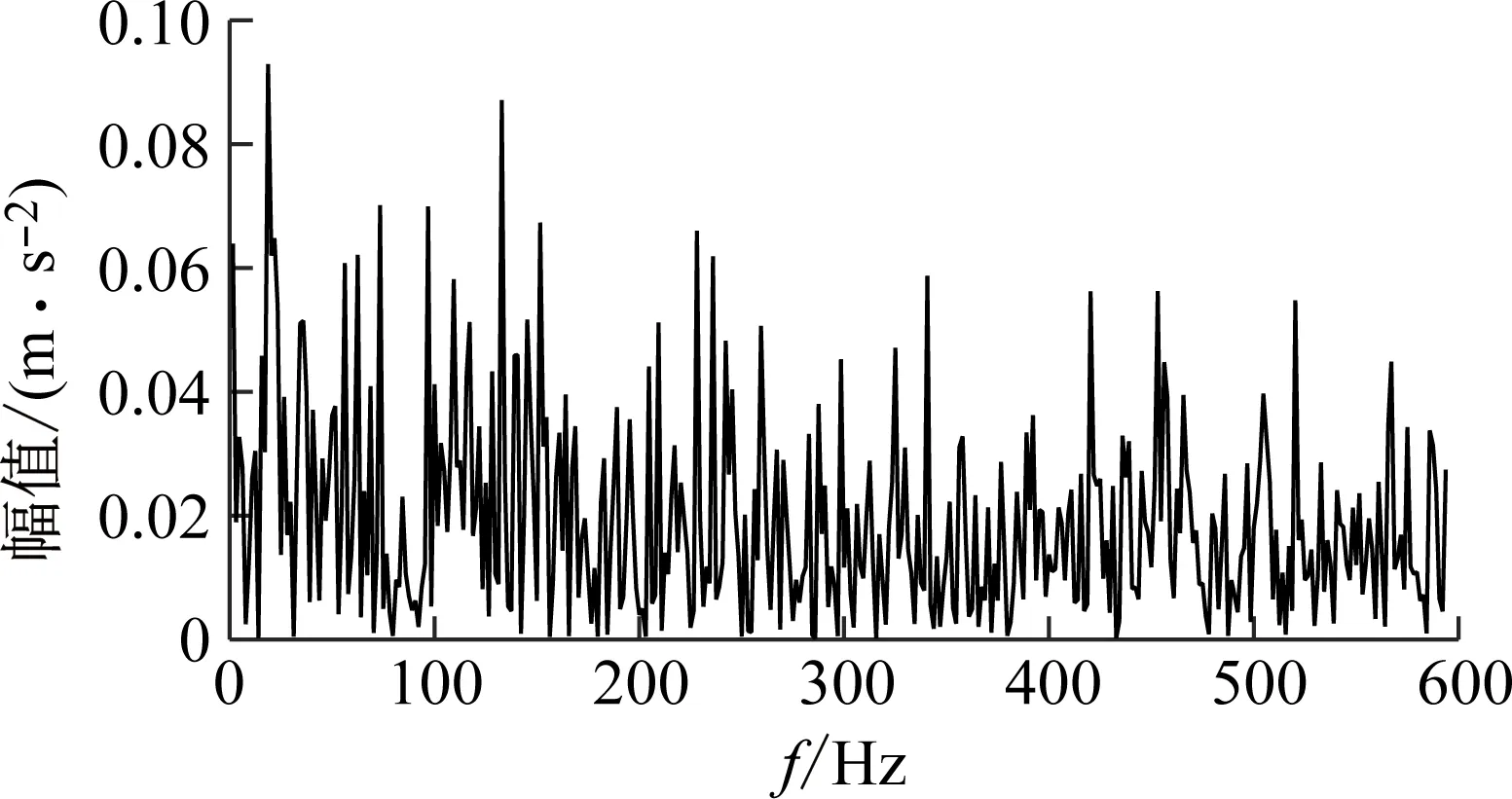
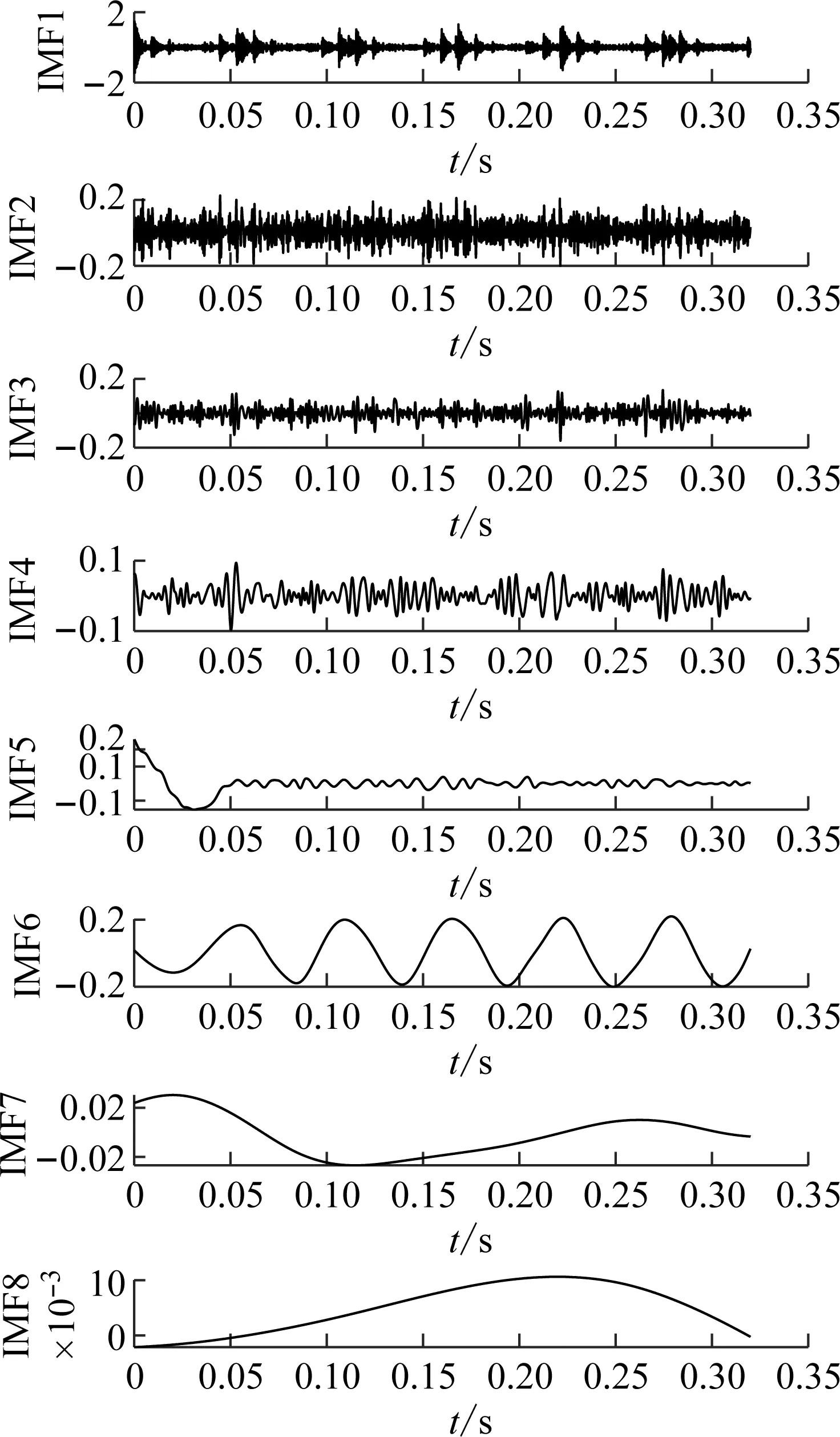
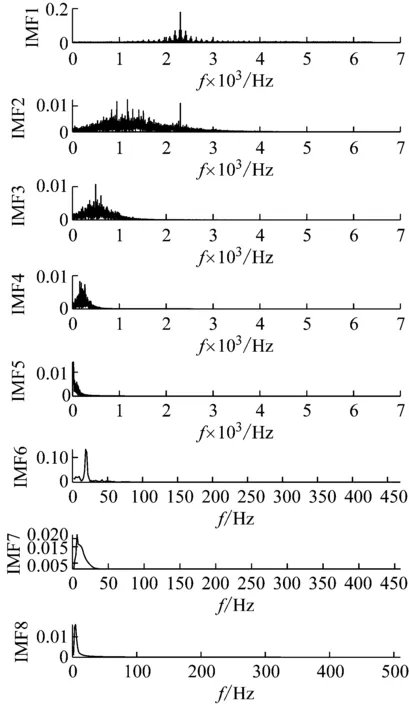
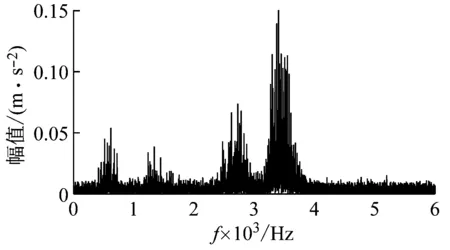
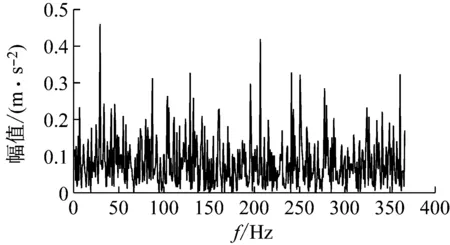
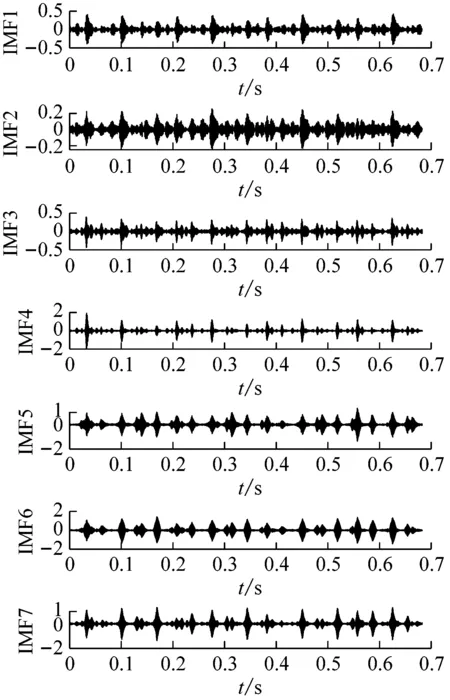
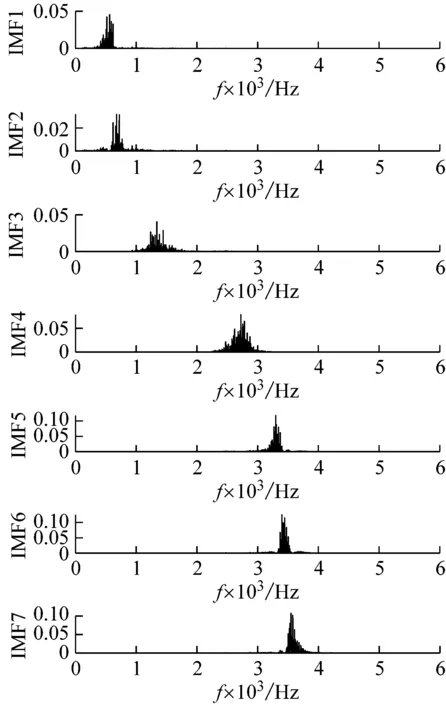
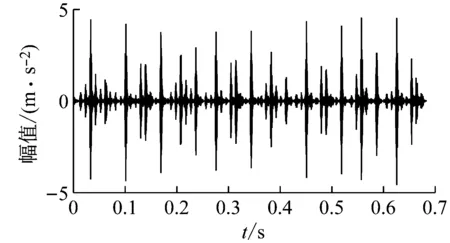
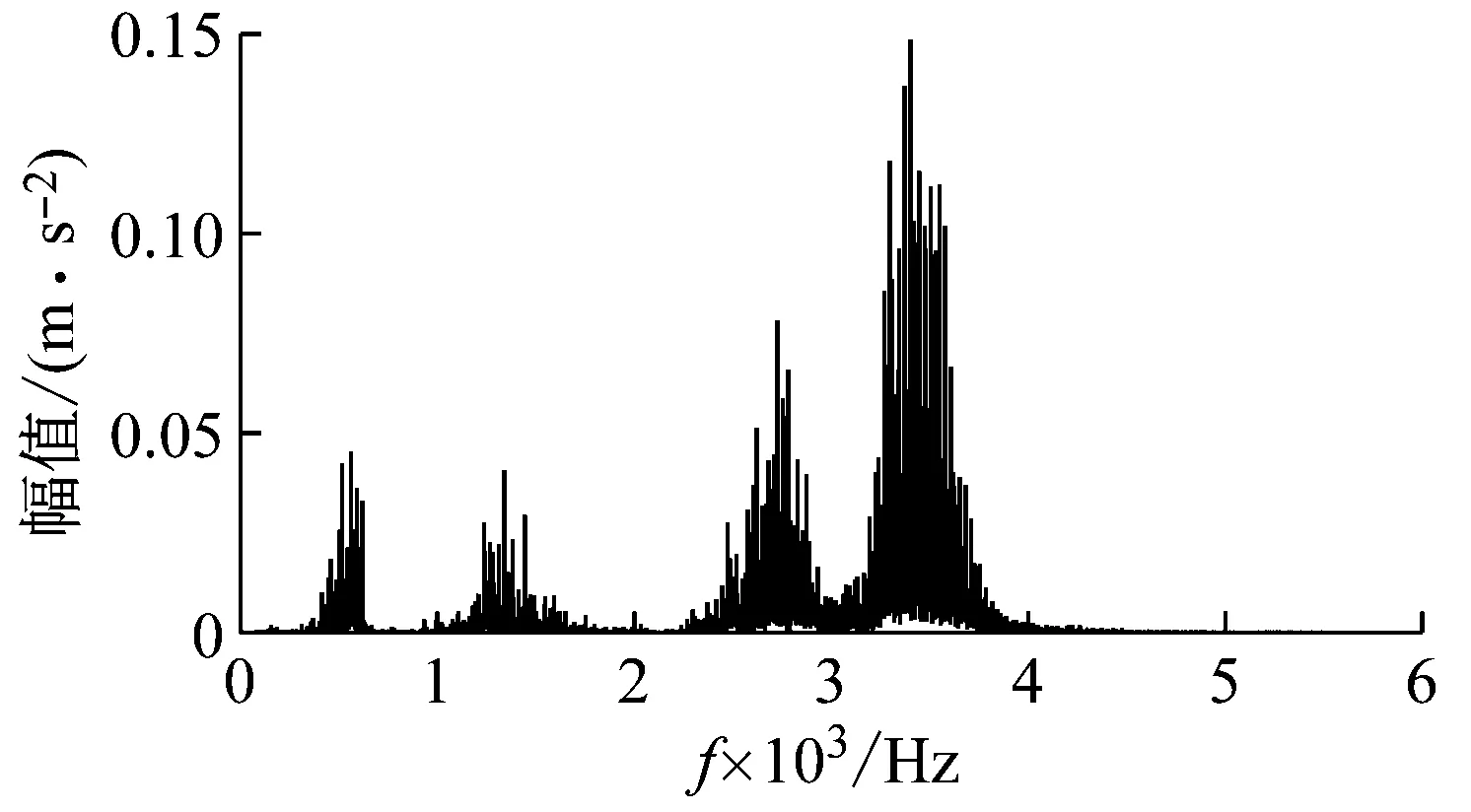
(2) 各模態分量相關系數ri分別與閾值r0進行比較,如果ri≥r0,對應的模態分量歸于有效模態組{uv1,uv2,…,uvp};如果ri (3) 當含噪模態組{un1,un2,…,unq}只有1個模態分量時,直接去掉該模態分量;有兩個及以上模態分量時,因相關系數最小的模態分量unq與原始信號關聯性最弱,通常為噪聲干擾信號,將其先去除,含噪模態組變為{un1,un2,…,un(q-1)},針對該含噪模態組按1.3節方法進行小波閾值去噪處理,其中,設定小波基函數為db8、小波分解層數為5層、小波閾值公式如下 (19) 式中:N為信號長度;σ為信號噪聲方差,其計算式為 σ=median(|Wj,k|)/0.674 5 (20) 式中,Wj,k為信號分解后得到的小波系數。 (21) 本文采用的信號降噪結果評價指標包括:信噪比SNR、能量百分比ESN、均方根誤差RMSE以及波形相似系數NCC。 信噪比SNR計算式如下 (22) 式中:x(t)為含噪信號;x′(t)為降噪后信號;N為數據點數。SNR值越大表示降噪效果越好。 能量百分比ESN計算式如下 (23) 式中:E′為降噪后信號能量;E為含噪信號能量,ESN值越大表示降噪效果越好。 均方根誤差RMSE計算式如下 (24) RMSE值越小表示降噪效果越好。 波形相似系數NCC計算式如下 (25) NCC值越大表示降噪效果越好。 基于滾動軸承外圈故障機理與信號特征,構建了式(26)所示仿真信號[20] (26) 式中:x(t)為軸承外圈故障含噪信號;y(t)為不含噪信號;x1(t)為共振干擾脈沖信號,設fr為軸轉頻,取fr=18 Hz,則相應的干擾脈沖間隔周期T1=1/fr=0.056 s;x2(t)為外圈故障脈沖信號,設f0為外圈故障頻率,取f0=107 Hz,則相應的故障脈沖間隔周期T2=1/f0=0.009 3 s;s(t)為諧波信號,其幅值取B0=0.4 m/s2;n(t)為高斯白噪聲信號;Ai為調頻信號,其頻率為fr,幅值取B1=0.6 m/s2;C為衰減系數,取C=800;fn為系統固有頻率,取fn=2 300 Hz。仿真信號采樣頻率設為12 000 Hz,采樣點數為16 384個。 圖3為不含噪仿真信號y(t)的時域波形、幅值譜和包絡譜圖,圖4為含噪仿真信號x(t)的時域波形、幅值譜和包絡譜圖。由圖3可知,不含噪聲仿真信號外圈故障特征明顯,尤其是包絡圖上,軸轉頻fr(18 Hz)、2倍頻2fr(36 Hz)、3倍頻3fr(54 Hz),外圈故障頻率f0(107 Hz)、2倍頻2f0(214 Hz)、3倍頻3f0(321 Hz)、4倍頻4f0(428 Hz),以及以故障特征頻率f0為中心、以轉頻fr為邊帶的各種調制頻率成分f0+fr(125 Hz)、f0-fr(89 Hz)、2f0+fr(232 Hz)、2f0-fr(196 Hz)等清晰可見,易于故障判定。由圖4可知,由于疊加了較強的高斯噪聲,外圈故障特征幾乎被淹沒,體現在圖4(c)的包絡譜圖上,幾乎無法提取出外圈故障特征頻率。 (a) 時域波形曲線 (b) FFT頻譜圖 (c) 包絡譜圖圖3 不含噪仿真信號y(t)Fig.3 Simulated signal y(t) without noise (a) 時域波形曲線 (b) FFT頻譜圖 (c) 包絡譜圖圖4 含噪仿真信號x(t)Fig.4 Simulated signal x(t) with noise 針對含噪仿真信號x(t)分別進行EMD和本文方法的降噪處理。圖5(a)為EMD分解得到的每個IMF分量時域波形,圖5(b)為每個IMF分量對應的FFT頻譜圖。由圖5可見,EMD分解結果中存在較為嚴重的模態混疊現象,各模態分量的頻段分離效果較差,以IMF2為例,系統固有頻率fn及其邊頻帶和其他中低頻率成分混疊在一起,不能有效提取有用信息;IMF2~IMF5,相鄰的IMF之間均產生了模態混疊,每個IMF均包含了低頻成分。與此同時,EMD分解過程中產生了虛假分量,如IMF3和IMF4中對應的頻率成分并不存在。 (a) IMF時域波形曲線 (b) IMF頻譜圖圖5 含噪仿真信號EMD分解Fig.5 EMD decomposition of simulation signal with noisy 利用本文提出的方法,首先進行基于IPSO算法的K和α參數尋優,K和α的尋優范圍設置為[3,10]和[200,6 000],獲得的最優參數值K=5,α=2 182;基于該最優參數進行VMD分解,得到的各IMF分量時域波形如圖6(a)所示,各IMF分量對應的FFT頻譜如圖6(b)所示。由圖6可見,本文方法可有效去除模態混疊現象,含噪信號經分解后實現了信號頻域及各個IMF分量的自適應剖分,每個IMF都圍繞在某一中心頻率處,軸轉頻成分被分解到IMF1,系統固有頻率fn被分解到IMF3,而系統固有頻率fn邊頻帶則被分解到IMF2和IMF4上,噪聲成分被分解到IMF5中;同時該方法也避免了虛假模態的產生。由此可見,相較于EMD算法,本文方法具有更好的分解效果與噪聲魯棒性。 (a) IMF時域波形曲線 (b) IMF頻譜圖圖6 含噪仿真信號VMD分解Fig.6 VMD decomposition of simulation signal with noisy 分別針對EMD和本文方法分解得到的各IMF分量與含噪仿真信號x(t)進行互相關計算,得到的互相關系數r如表1所示。 表1 各IMF分量與x(t)的互相關系數riTab.1 Cross correlation coefficient ri between each IMF component and x(t) 根據式(18)確定相關系數閾值r0,然后對表1中滿足系數閾值條件的IMF 進行信號重構。經計算,EMD分解的各模態函數分量r0=0.16,本文方法分解的各模態函數分量r0=0.17。因此,結合表1,EMD分析結果中選取IMF1、IMF6,其他各模態函數分量舍棄,以此重構信號;本文方法分析結果中將IMF1、IMF2、IMF3、IMF4歸為有效模態組,IMF5歸為含噪模態組,由于含噪模態組只有1個分量,不用進行小波閾值處理,直接舍棄,以有效模態組4個分量重構信號。最終得到2組降噪后信號,分別示于圖7和圖8。圖7(a)是EMD降噪信號時域波形,圖8(a)是本文方法降噪信號時域波形,與圖3(a)不含噪仿真信號y(t)的時域波形相比,可定性看出EMD降噪后仍存在一定程度上的噪聲干擾,本文方法降噪信號波形比EMD降噪更接近不含噪仿真信號。圖7(b)和圖8(b)是兩組降噪后信號的包絡譜圖,與圖3(c)不含噪仿真信號y(t)的包絡圖均極為接近,故障頻率f0及其各種調制頻率等特征頻率清晰可見。 (a) 時域波形曲線 (b) 包絡譜圖圖7 EMD方法降噪結果Fig.7 Noise reduction results of EMD method (a) 時域波形曲線 (b) 包絡譜圖圖8 本文方法降噪結果Fig.8 Noise reduction results of this paper method 應用式(22)~式(25),針對降噪后信號進行降噪指標計算,結果如表2所示(表中還列出了EEMD評價結果)。可以觀察到本文方法降噪結果信噪比更高、能量百分比更大、均方根誤差更小、平滑度更接近1,各項評價指標全面好于EMD和EEMD方法,說明本文方法降噪效果明顯優于EMD和EEMD降噪方法。 表2 降噪評價指標結果Tab.2 Evaluation index results of noise reduction 采用美國凱斯西儲大學的滾動軸承故障試驗數據驗證本文降噪方法的有效性,試驗系統如圖9所示。 圖9 滾動軸承試驗臺Fig.9 Rolling bearing test bench 實驗臺驅動端軸承型號為6205-2RS JEM SKF深溝球軸承,技術參數和規格信息如表3所示。 表3 滾動軸承技術參數和規格信息Tab.3 Technical parameters and specifications of rolling bearing 采用電火加工技術分別在軸承內、外圈布置單點故障,選擇驅動端軸承外圈故障數據,故障直徑為0.533 4 mm,深度為0.279 4 mm。該外圈故障對應電機轉速為1 721 r/min(即轉頻fr為28.68 Hz),采樣頻率為12 000 Hz,采樣點數為16 384。結合表3中軸承各參數,通過下式計算得到軸承外圈故障頻率f0為102.81 Hz。 (27) 試驗采集到的原始故障信號相關信息如圖10所示,其中圖10(a)是其時域波形曲線,圖10(b)是其FFT分析幅值譜圖,圖10(c)是其包絡譜圖。由圖可知,故障時域波形沖擊特征較為明顯,但也存在大量噪聲;幅值譜圖上譜線主要分布在4個頻段區域:高頻區(中心頻率約3 400 Hz)、次高頻區(中心頻率約2 800 Hz)、中頻區(中心頻率約1 300 Hz)和低頻區(中心頻率約600 Hz),信號能量主要集中在高頻和次高頻區,低頻區的能量較小,而軸承的外圈故障特征頻率幾乎無法提取;包絡圖上能觀察到軸轉頻和故障特征頻率,但由于噪聲干擾,圖上干擾譜線較多,故障特征頻率的調制頻帶等故障相關頻率成分均很難觀察到。 (a) 時域波形曲線 (b) FFT頻譜圖 (c) 包絡譜圖圖10 試驗原始信號圖形Fig.10 Experimental original signal graph 利用本文方法,通過IPSO算法獲得VMD最優參數值K=7,α=2 684,進一步對原始故障信號進行VMD分解,得到的各IMF分量時域波形如圖11(a)所示,對應的FFT幅值譜如圖11(b)所示。將各IMF分量與原始信號進行互相關計算,得到的互相關系數如表4所示。 表4 各IMF分量與原始信號的互相關系數Tab.4 Cross correlation coefficient between each IMF component and original signal (a) IMF時域波形曲線 (b) IMF頻譜圖圖11 試驗原始信號VMD分解Fig.11 VMD decomposition of test original signal 結合圖11和表4可以看出含噪信號經VMD分解后實現了信號頻域及各個IMF分量的自適應剖分,每個IMF都圍繞在4個頻段區域的某一中心頻率處,低頻段區被分解到IMF1和IMF2,二者有一定的頻率重疊,其互相關系數值也較小,中頻段區被分解到IMF3,次高頻段區被分解到IMF4,高頻段區由于能量占比最大,它被分別分解到IMF5、IMF6和IMF7,其互相關系數值也最大。 由式(18)可確定相關系數閾值r0=0.18,結合表4,將IMF4、IMF5、IMF6、IMF7歸為有效模態組,IMF1、IMF2、IMF3歸為含噪模態組,其中IMF2相關系數最小,直接舍棄,對含噪模態組的IMF1和IMF3進行小波閾值處理,并與有效模態組的4個IMF分量一起重構信號,得到降噪信號,其時域波形、FFT幅值譜、包絡譜示于圖12。與試驗原始信號圖10相比,降噪后時域波形沖擊特征更明顯,幅值譜能量分布基本不變,噪聲干擾更少,譜線更清晰;降噪效果在包絡譜圖12(c)上體現最明顯,其譜圖較為干凈,干擾成分較少,可清晰發現軸轉頻fr(約29 Hz)、2倍轉頻2fr(58 Hz)成分,也可發現明顯的約103 Hz故障區域,對應軸承外圈故障頻率f0,同時存在故障頻率的2倍頻2f0(206 Hz)、3倍頻3f0(309 Hz)成分,以及以故障特征頻率f0為中心以轉頻fr為邊帶的調制頻率成分f0+fr(132 Hz)和f0-fr(74 Hz),這與外圈故障特征頻率被轉頻所調制的特性相符。說明本文方法有很好的降噪效果,據此提取的故障特征可用于軸承外圈故障的判定。 (a) 時域波形曲線 (b) FFT頻譜圖 (c) 包絡譜圖圖12 降噪后信號圖形Fig.12 Signal graph after noise reduction 本文針對滾動軸承強背景噪聲故障信號,提出了一種基于參數自尋優變分模態分解的信號降噪方法。為實現VMD模態數K和二次懲罰因子α的自適應尋優,提出了一種改進粒子群算法(IPSO),通過構建適合滾動軸承故障信號特點的適應度函數、慣性權重公式、邊界粒子以及粒子群優化處理方法,提高了VMD參數自尋優搜索能力;基于最優K和α,對含噪信號進行VMD分解,利用相關系數篩選法,對K個IMF分量進行有效模態和含噪模態識別,對后者進行小波閾值去噪,并與前者一起進行信號重構,實現信號降噪。從數值仿真和試驗數據角度,將本文所提方法與EMD和EEMD降噪方法進行對比分析,從信噪比、能量百分比、均方根誤差以及波形相似系數4個評價指標,定量說明本文方法在滾動軸承故障信號降噪中具有更好的降噪效果,是一種有效的降噪方法。
4 仿真信號降噪分析
4.1 降噪評價指標
4.2 仿真信號構建
4.3 仿真信號分析
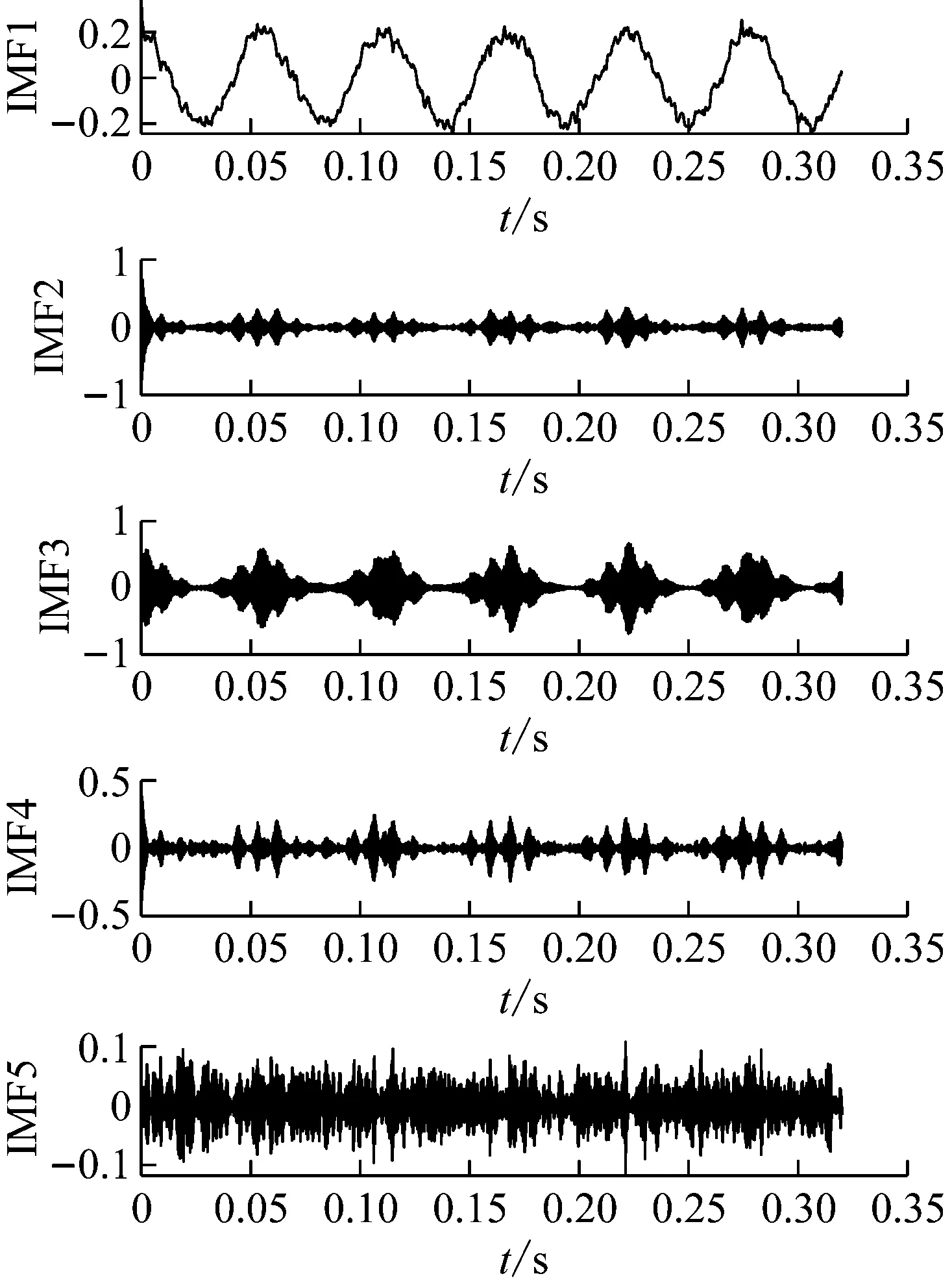
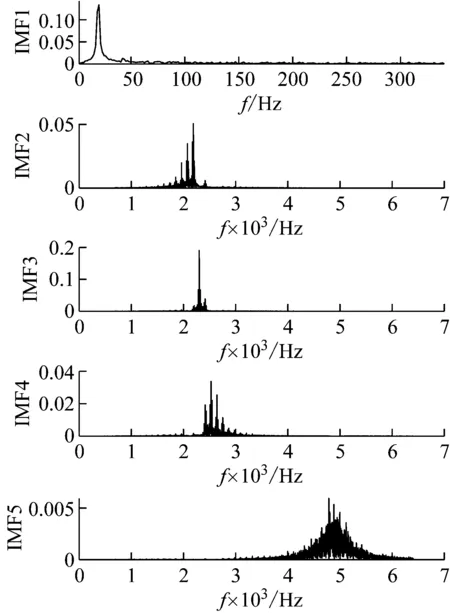
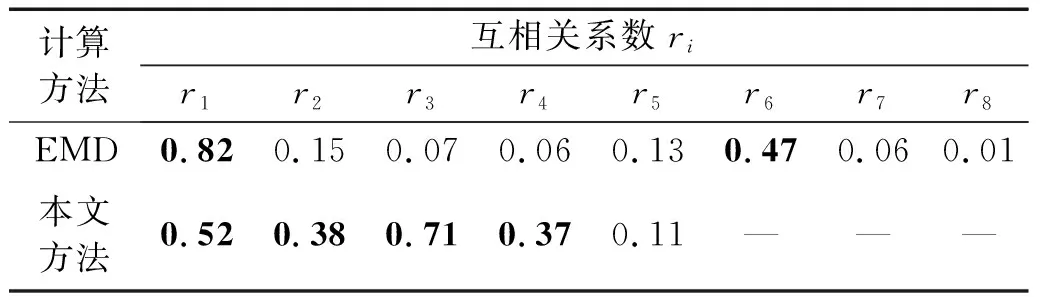
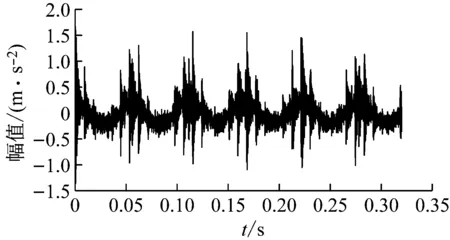
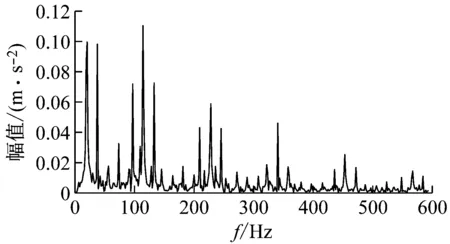
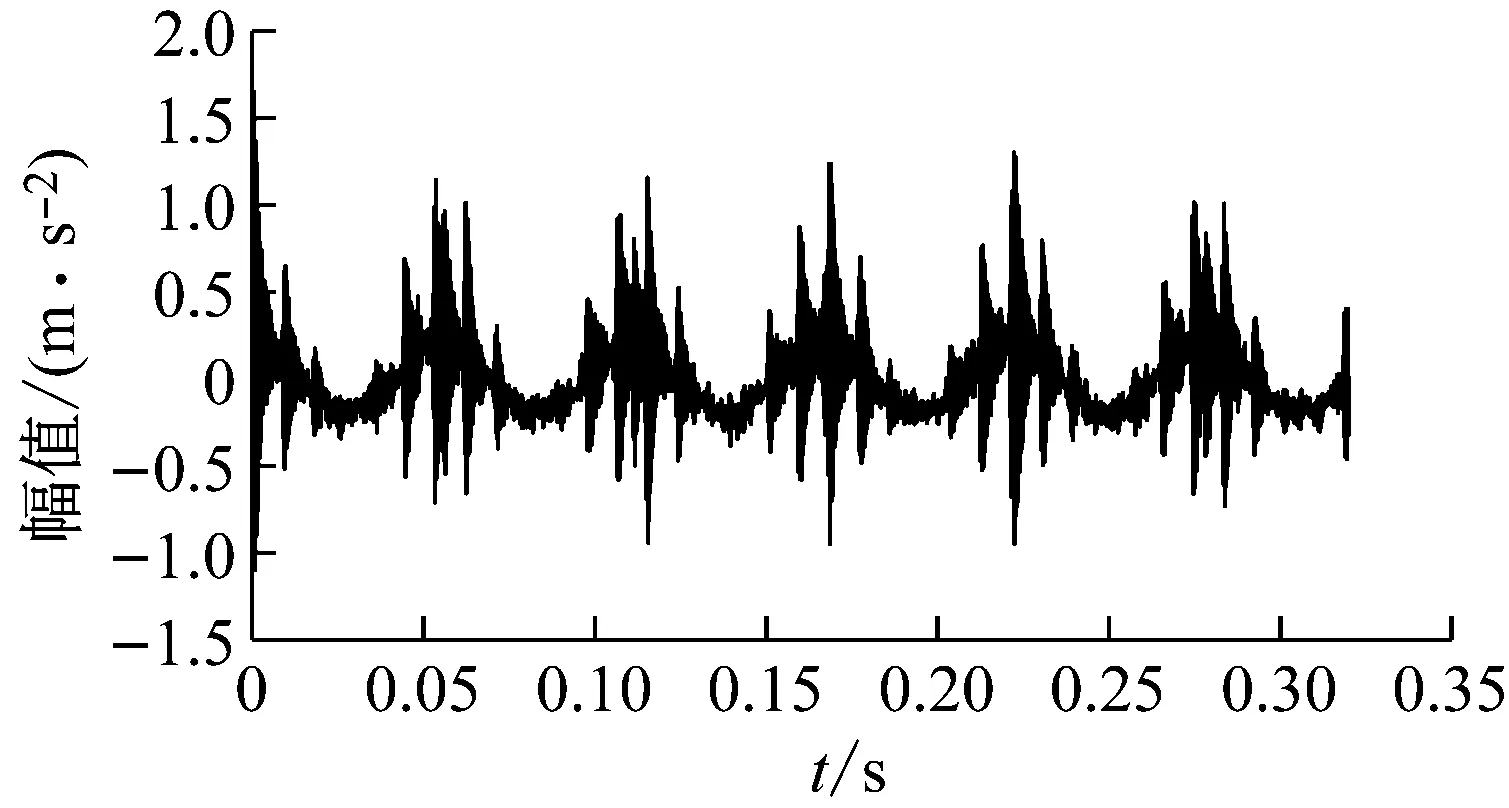
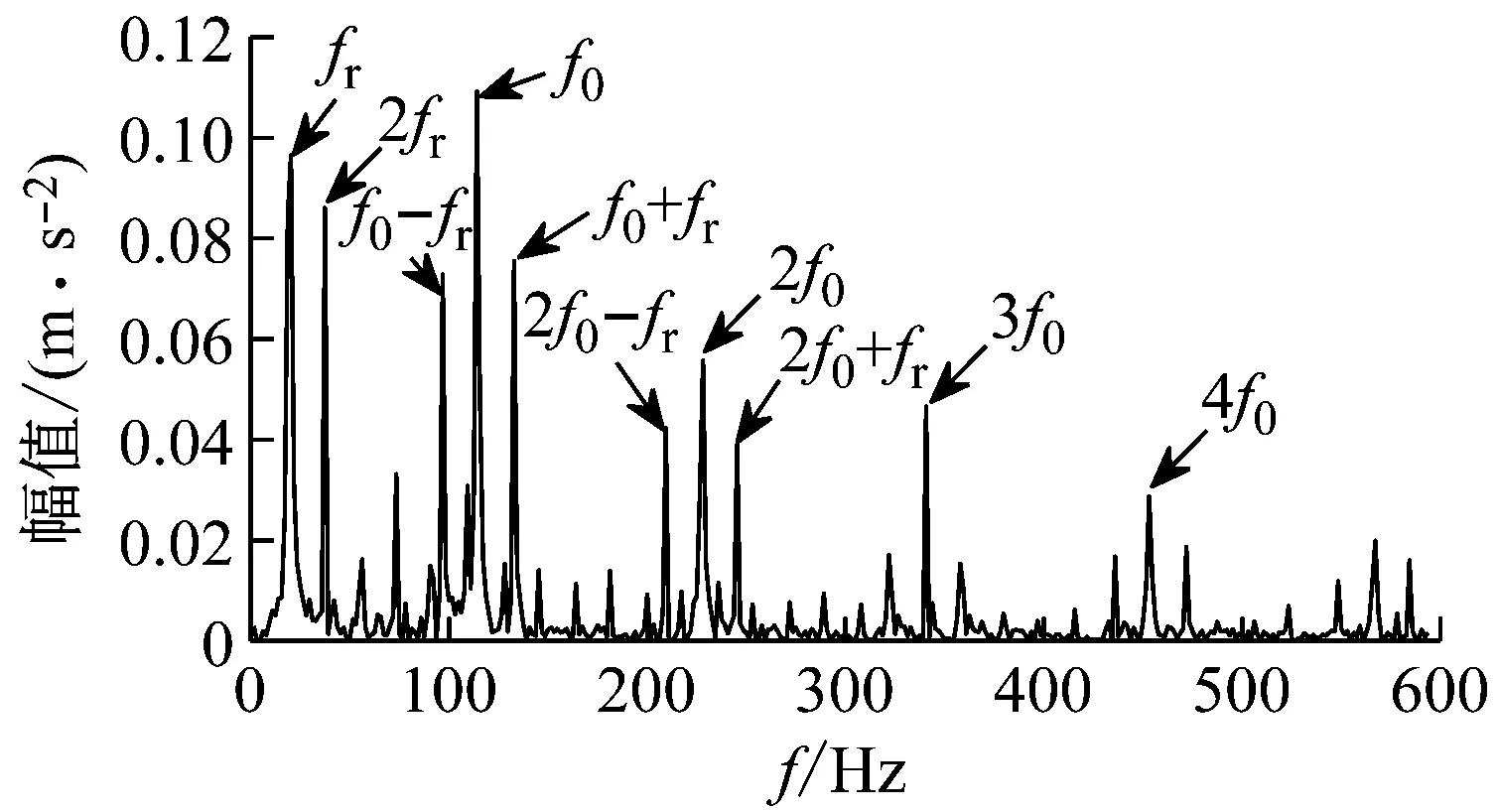
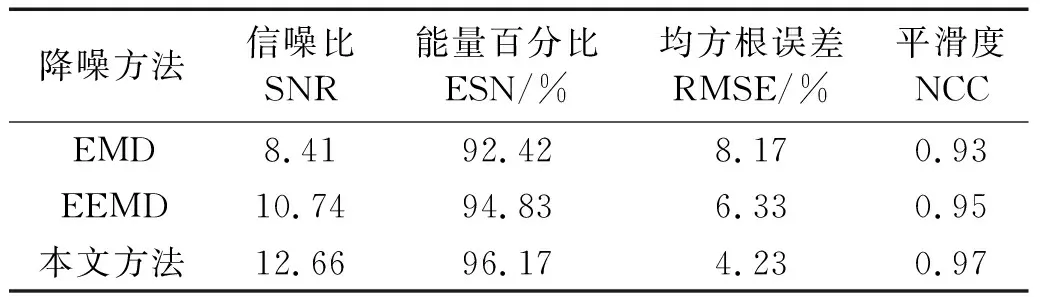
5 試驗信號降噪分析





6 結 論

