基于動態模態分解的輸電桿塔松動檢測

楊金顯, 申劉陽, 鄭澤南, 李田田, 楊雨露

(1.河南理工大學 電氣工程與自動化學院,焦作 454000;2.河南省煤礦裝備智能檢測與控制重點實驗室,焦作 454003)

輸電桿塔長期處于復雜的工作環境中,連接結構(如螺栓、鉚釘等)在動載荷的作用下容易出現變形、滑移和碰撞等現象,導致結構松動。松動會破壞桿塔的使用性9能,危及塔架結構的安全,甚至導致塔架倒塌,造成人員和財產損失。傳統桿塔維護主要靠人工定期巡檢,這種方式操作難、效率低,存在較大的主觀性[1]。隨著輸電系統的日益龐大,研究一種準確高效的桿塔松動檢測方法是建設智慧電網的基礎。

松動是結構損傷的一種表現,已發表的損傷檢測方法表明,松動會導致剛度降低,使結構的振動響應發生變化[2]。目前較為有效的結構健康監測(structural health monitoring,SHM)是在結構上安裝傳感器來測量結構對外部激勵的振動響應,根據振動響應的變化來判斷結構狀況[3-4]。為了避免使用激振設備對結構造成損傷,影響結構正常工作,對于在役工程結構,通常利用環境激勵引起振動響應,基于環境振動的結構健康監測無需額外的激振設備,測量結果更加符合實際工況[5]。戶外結構所處的振動環境一般呈現三軸向六自由度特征[6],在隨機激勵的影響下,輸電桿塔的振動信號會出現不同自由度的耦合振動[7],因此單一方向的振動無法完整描述信號特征。微電子機械系統(micro electro mechanical system,MEMS)慣性測量系統能夠監測桿塔三軸加速度和三軸角速度,具有體積小,安裝方便,功耗低且耐用的優點,因此被用來進行結構健康監測[8]。

模態參數是質量、剛度和阻尼的函數,結構松動使得剛度降低,引起模態參數變化,因此基于振動的損傷檢測研究主要集中在從工程結構的振動響應中提取模態變化[9-10]。松動使結構剛度下降,導致固有頻率減小,但早期松動引起的固有頻率的變化十分有限,不足以作為松動指標[11]。結構松動使得振幅增大,但振幅容易受到激勵的影響,甚至出現不同松動狀態(松動位置和松動程度不同)下振幅相同的情況,因此單一方向的振幅不能很好地識別松動狀態。定義方向振型為六自由度以同一模態頻率振動的幅值組成的向量,方向振型可以看作振動信號在不同自由度的解耦,與模態頻率一一對應。桿塔出現松動時,各軸向的水平振動和扭轉振動是與松動位置和松動程度有關的,因此方向振型能夠表征松動位置和松動程度。

面對復雜的振動信號,如何利用有效的信號處理方法提取合適的松動特征是識別桿塔松動狀態的關鍵。許多信號處理技術,如小波變換(wavelet transform,WT)、希爾伯特-黃變換(Hilbert-Huang transform,HHT)、經驗模態分解(empirical mode decomposition,EMD)、變分模態分解(variational mode decomposition,VMD)等,已被用于從結構的動力響應中提取損傷特征,并將其應用于螺栓結構松動的損傷檢測[12-15]。但輸電桿塔這種大型復雜結構的振動是多自由度的非線性振動,且環境激勵會對振動信號產生不可避免的噪聲干擾,影響檢測結果。

與其他數據驅動分解算法不同,動態模態分解(dynamic mode decomposition,DMD)算法結合了本征正交分解和傅里葉分析的優勢,能將桿塔多自由度振動信號分解為一系列單頻模態,得到與模態頻率對應的方向振型[16]。與常用的信號分析方法對比,DMD算法擁有更高的分辨率,降噪效果更加明顯[17],因此DMD算法在模態分析,故障識別等領域得到了廣泛應用。文獻[18]采用DMD算法對軸承故障信號進行模態分析并識別故障。文獻[19]利用DMD算法將時間-空間耦合的電磁信號分解為若干模態分量,實時監測電磁環境狀態。文獻[20]對離心泵葉輪內復雜的流動信號進行動態模態分解,識別脈動頻率等動態模態特征。

基于上述分析,首先利用MEMS慣性測量裝置在桿塔易松動的節點處測量桿塔六自由度振動信號,采用DMD算法對振動信號進行降噪。為了從振動模態中提取方向振型作為松動特征,本文提出改進的分段高階動態模態分解(segment high-order dynamic mode decomposition,SHDMD)算法,在環境激勵下得到桿塔多自由度振動信號的真實模態并提取方向振型。為了識別輸電桿塔的松動位置和程度,利用方向振型建立了輸電桿塔松動狀態的灰色關聯檢測模型。最后設計了模型輸電桿塔試驗和真實輸電桿塔試驗,對所提方法的有效性進行了驗證。

1 輸電桿塔振動數據采集及處理

1.1 MEMS系統采集數據

基于MEMS慣性測量的輸電桿塔松動檢測裝置由三軸加速度計、三軸陀螺儀、電源模塊和數據傳輸模塊構成。設備需用固定夾具整齊牢固地安裝在測點,并采取必要的保護措施,盡量避免外部干擾。安裝位置要便于調整,不影響正常的維護工作。在現場維護或測試中,操作員可使用手持設備或筆記本電腦通過有線傳輸獲取監測數據。監測中心也可以通過無線通信實時或定期接收輸電桿塔的振動數據,及時采取措施,防止事故進一步發展。

MEMS慣性測量系統采集輸電桿塔的振動加速度和角速度,得到六組一維等間隔時間為Δt的加速度序列,分別表示為:(ax1,ax2…axL),(ay1,ay2…ayL),(az1,az2…,azL),(ωx1,ωx2…ωxL),(ωy1,ωy2…ωyL),(ωz1,ωz2…ωzL),其中a為振動信號的三軸加速度,ω為振動信號的三軸角速度。

1.2 原始DMD算法處理數據

DMD算法通過對原始信號分解和重構,實現去除噪聲的目的。以X軸加速度為例,用加速度序列ax構造Hankel矩陣H∈RM×N:

(1)

DMD算法步驟如下:

步驟1將矩陣H分為兩個在時間上連續的矩陣Ψ1、Ψ2;

(2)

步驟2由Koopman理論可知,兩個在時間維度上相鄰的矩陣可以看作近似線性

Ψ2=AΨ1

(3)

步驟3對矩陣Ψ1進行奇異值分解

Ψ1=UΣV*

(4)

式中:U、V均為正交矩陣;Σ是奇異值降序排列的對角矩陣。

步驟4計算Koopman矩陣A

A=Ψ2VΣ-1U*

(5)

步驟5對矩陣A進行特征值分解

A=WΛW-1

(6)

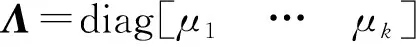
Ψ1=

(7)

式中:φl為模態;bl為幅值;μl為特征值;Vand為范德蒙矩陣,表示振動信號的時間演化過程。

重構矩陣的第一行為降噪后的加速度序列,其他振動方向降噪過程相同,最終得到降噪后的三軸加速度和三軸角速度。

2 輸電桿塔松動狀態識別

2.1 SHDMD算法提取松動特征

為了提取輸電桿塔振動信號的方向振型,通過六自由度振動加速度構造一個時間-空間矩陣,對桿塔振動狀態進行描述。將采集到的三軸加速度和三軸角速度按照式(8)構造時間-空間矩陣X∈R6×N,矩陣的列向量代表當前采樣時刻各自由度的振動狀態。

(8)

DMD算法能夠從時間-空間矩陣中得到振動信號的模態頻率和對應的方向振型。通過1.2節描述的原始DMD算法可以發現該方法用于環境激勵下輸電桿塔松動特征提取的局限性:①環境激勵是具有隨機性的復雜的非穩態信號,因此桿塔振動信號除了結構自身的動力學特性,還包含外界干擾帶來的虛假模態,很難得到準確的方向振型;②當矩陣的空間維度S小于時間維度T時,奇異值分解得到的非零奇異值個數R≤min(S,T),這一特性使得模態數目受到限制,無法完全呈現信號的動態特征[21]。輸電桿塔振動信號是六自由度的,因此時間-空間矩陣的空間維度等于6,遠遠小于時間維度,對于這種情況,DMD分解可能會出現錯誤的結果。

環境激勵不可能在每段數據中都相同,但結構固有模態引起的振動響應是穩定的,只與結構健康有關。改進的總體思想是將振動過程分成若干子過程,對每個子過程進行空間維度擴展,然后對擴展后的子過程實施DMD分解,得到不同子過程的模態,并在穩定圖中進行篩選,最終得到真實模態和對應的方向振型。其中數據分段的目的是得到不同時段不同激勵下的振動響應,同時消除隨機誤差。空間維度擴展是為了使模態分解不受維度限制。SHDMD算法描述如下:

(1) 時間-空間矩陣分段

生物源于生活，服務于生活.在當前教學中，由于受傳統教學模式的影響，生物教學課時安排較為緊張，生物教師很少組織學生參加野外活動、參觀生產基地等生物知識類的教學活動.由于高中生物教學缺少色彩，學生只能被動、機械地學習生物，自主性學習興趣不高漲，難以有效地將生物知識與生活相聯系，生物思維得不到有效激發.

我們希望所得到的DMD模態能夠揭示更本質的振動特征,并且擁有較高的分辨率,因此選擇長度為K的矩形窗口,在時間-空間矩陣X的時間維度上滑動,滑動步長為K/2,即在信號分段時使每段之間都有部分交叉重疊,降低分段長度的增大對分辨率的影響。最終將矩陣劃分為n個子矩陣,其中n=(2N-K)/K,每個子矩陣代表當前時刻的時間-空間狀態,劃分方式如圖1所示。

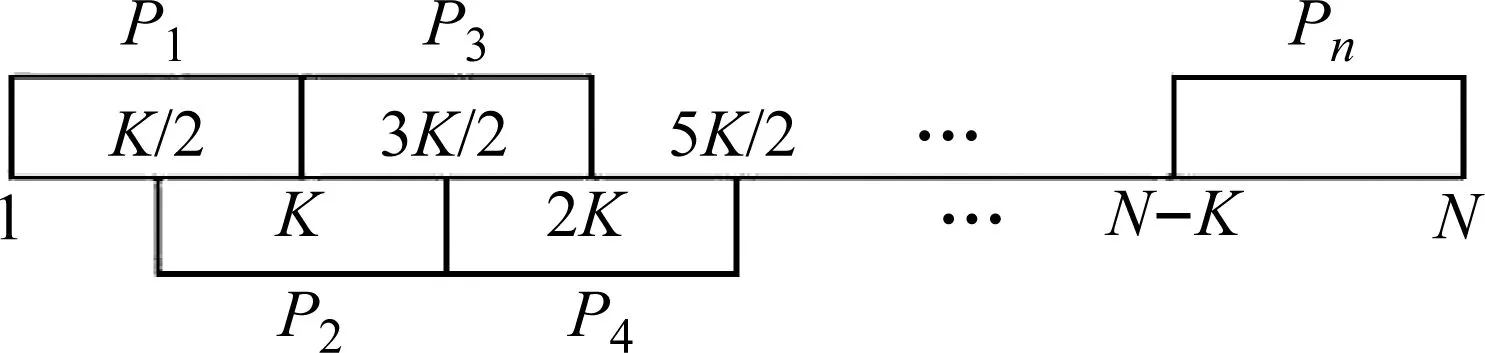
圖1 時間-空間矩陣分段Fig.1 Time-space matrix segmentation

將P時刻的時間-空間狀態子矩陣記作YP∈R6×K:

(9)

式中,P=1,2,…,n。

(2) 子矩陣空間維度擴展

(10)

式中,d為延遲嵌入參數,一般選擇使dS>2T成立的最小整數d[22]。

(3) 子矩陣DMD分解

為了得到振動信號的方向振型,根據1.2節描述的DMD算法步驟,將P時刻的時間-空間子矩陣分解為l個類傅立葉模態的展開。

(11)

(12)

式中:l為振動加速度信號分解得到的模態個數;fm為第m階模態頻率;τm和φm分別為與模態頻率對應的模態衰減率和模態振型;bm為模態幅值,表示各模態在振動信號中的參與度。

(4) 不同時刻的模態穩定圖

穩定圖的原理為:在對應于某一階模態的軸線上,前一個子過程識別的模態參數同后一個子過程識別的模態參數相比較,如果模態參數的差異小于預設的限定值,則這個點就稱為穩定點,穩定點組成的軸線稱為穩定軸,穩定軸對應的模態為真實模態。穩定軸的確定需要滿足式(13)～式(15)

(13)

(14)

1-MAC(φP,φP+1)=

(15)

式中,較小的df和dτ表示兩個模態具有相似的頻率值和衰減率;當MAC接近1時,表示兩個模態具有相似的方向振型,而如果MAC值接近于0,則表示兩個模態的相似性較低。fth,τth,φth分別代表頻率、衰減率和振型的閾值,只要確定合適的閾值,就可以消除虛假模態,通常根據實際工程情況和經驗確定閾值,常用的閾值分別為1%、5%、2%[23]。輸電桿塔的振動頻率屬于低頻,模態頻率的范圍較小,為了避免消除真實模態,可將閾值范圍上調至5%、10%、7%。根據穩定圖識別出r個真實模態,由于擴展的矩陣是原始數據的d個時移堆疊,分解得到的模態振型也是d個重復的模塊,因此選擇模態振型φm的前6個元素組成方向振型,記作φm,提取出與模態頻率一一對應的方向振型φ1,φ2,…,φm…,φr作為松動特征。

2.2 灰色關聯模型識別松動狀態

灰色關聯分析的實質為比較數據曲線幾何形狀的接近程度,幾何形狀越接近,關聯度越大,因此分析不同松動狀態下方向振型的灰色關聯度可以實現松動狀態識別。根據式(16)和式(17),建立輸電桿塔松動的灰色關聯檢測模型

φ=(φ(k)|k=1,2,…,6)

(16)

(17)

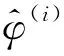
輸電桿塔松動狀態檢測的步驟如下:

步驟1提取待檢測狀態的r階方向振型:φ1,φ2,…,φr。

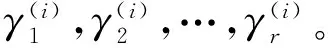
步驟4構造松動檢測的關聯度矩陣

(18)

綜上所述,為了識別輸電桿塔的松動狀態,首先安裝MEMS慣性測量裝置實時或固定時間采集輸電桿塔的振動信號,監測中心對接收到的信號進行處理,利用SHDMD算法從處理后的振動數據中得到方向振型作為松動特征,灰色關聯檢測模型通過將待檢測狀態的方向振型與不同松動程度的參考振型比較,判斷輸電桿塔當前的松動狀態。輸電桿塔松動狀態識別的流程圖,如圖2所示。針對不同結構類型和尺寸的輸電桿塔,在監測過程中建立與其對應的參考振型數據集,不同型號輸電桿塔的參考振型數據集構成參考振型數據庫。當輸電桿塔的結構和尺寸確定后,首先在數據庫中搜索同型號桿塔的數據集,若匹配成功,按照圖2所示流程進行松動監測;若無匹配的數據集,則需要在監測的同時建立對應的參考振型數據集。數據集的建立遵循以下流程:首先按照圖2所示數據采集和特征提取的步驟得到被監測輸電桿塔在初始健康狀態下的方向振型,并加入參考振型數據集。計算后續監測過程中提取的方向振型與健康狀態下的參考振型的灰色關聯度,若關聯度較小,說明發生松動,應盡快檢修,并將該方向振型與此時的松動狀態對應,加入參考振型數據集。依次類推,完成當前被監測輸電桿塔的參考振型數據集的建立,最后將該數據集加入數據庫,方便后續同種型號輸電桿塔的松動監測。

圖2 桿塔結構松動狀態識別流程圖Fig.2 Flow chart for identification of loose state of tower structure

3 試驗與結果分析

3.1 模擬輸電桿塔試驗

為了驗證上述桿塔結構松動識別方法的有效性,按照1∶20的比例搭建了110 kV鼓型輸電桿塔的塔線體系模型,如圖3(a)所示。塔架結構采用等邊角鋼,塔身高1.25 m,共6層,每層4個結構連接點,每個節點有6個螺栓,模型節點編號如圖3(b)所示,Jl1表示第l層的第一個節點。為了采集輸電桿塔的振動響應信號,在測試現場安裝了實驗室設計的MEMS慣性測量系統,每層布設1個測點,位于每層的節點Jl1處,MEMS三軸傳感器的參考方向如圖3(a)所示。利用大功率風扇模擬環境激勵,隨機切換風扇檔數模擬不同風速對輸電桿塔施加激振作用,采集并記錄三軸加速度和三軸角速度,數據被傳輸至監測中心保存并完成分析。

圖3 模型桿塔試驗Fig.3 Test of model tower

試驗過程中,以螺栓基本擰死的狀態為未松動狀態,以旋松的圈數表示松動程度,通過調整螺栓松動位置、松動數量以及松動程度,分別在6個測點模擬如表1所示的8種工況,松動節點局部放大圖如圖3(c)所示。

表1 模擬桿塔試驗工況Tab.1 Test conditions of model tower

為了減小加速度和角速度量綱的差異,消除不同軸向振動信號的大小不在同一數量級的影響,采用max-min法將三軸加速度和三軸角速度的值歸一化。調整風扇的風速模擬環境激勵的變化,測點1處采集到的工況1的振動加速度,可以看出振動信號的變化對應了激勵的變化,如圖4所示。

圖4 測點1處工況1的振動加速度Fig.4 Vibration acceleration under condition 1 at measuring point 1

為了驗證SHDMD算法在環境激勵中提取真實模態的有效性,分別在6個測點采集工況1下的振動信號,并進行SHDMD分析。信號長度N=5 000,為了便于分析,選擇子矩陣的窗口長度K=100,子矩陣的個數n=99,根據空間維度擴展的規則,延遲嵌入參數選擇d=17,最終得到測點1～6的模態穩定圖,如圖5所示。可以看出,各測點得到的模態頻率表現出了高度一致性,說明SHDMD算法能夠克服環境激勵的隨機性,可以很好地從時間-空間矩陣中得到真實的模態。

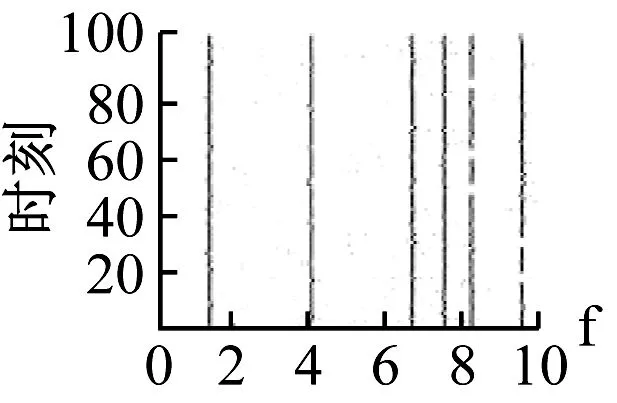
(a) 測點1模態穩定圖

(b) 測點2模態穩定圖

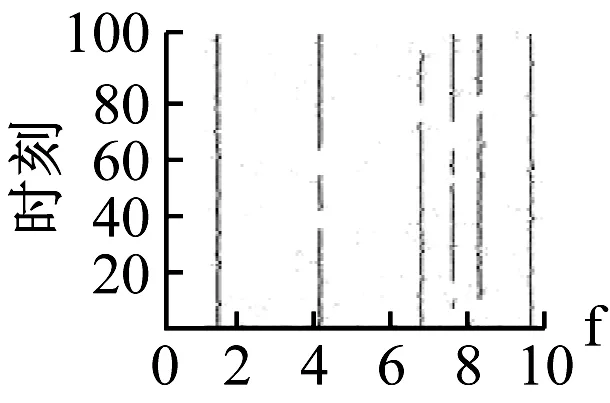
(c) 測點3模態穩定圖

(d) 測點4模態穩定圖

(e) 測點5模態穩定圖

(f) 測點6模態穩定圖圖5 測點1～6模態穩定圖Fig.5 Mode stability diagram of measuring points 1-6

為了分析松動節點和松動程度對松動特征的影響,以第一層測點為例,將圖2所示的分析流程應用于表1所示的工況1～工況8采集到的振動信號,計算不同工況的方向振型與工況1的方向振型的灰色關聯度γi,結果如表2所示。

表2 不同工況的灰色關聯度Tab.2 Grey correlation degree of different working conditions

比較工況1、2、3、4可知,螺栓松動程度越大,與健康狀態的灰色關聯度越小,比較工況2和5可知,松動螺栓數量越大,與健康狀態的灰色關聯度越小,原因是螺栓的松動程度和松動數量與節點的松動程度有關,松動程度和數量越大,結構的松動程度越大,因此與健康狀態的灰色關聯度越小。

比較工況2、6、7、8可知,工況2與健康狀態的灰色關聯度最小,原因是該工況下的松動節點與測點位置重合,傳感器能夠更加直接地感受到松動帶來的影響,而與測點位置距離最遠的工況7與未松動狀態的灰色關聯度最大。經過驗證,其他層測點得到的影響結果與第一層一致。

為了驗證本文所提方法對輸電桿塔結構松動狀態的識別效果,對第一層的4個節點設置如表3所示的17種工況。

表3 模擬桿塔試驗工況Tab.3 Test conditions of model tower

對第一層測點得到的振動信號進行分析,得到17組不同松動狀態下的模態,每組模態提取出前6階方向振型作為參考振型,利用灰色關聯檢測模型對測試樣本1(J11,1個,1圈),測試樣本2(J12,2個,1圈),測試樣本3(J13,2個,2圈),測試樣本4(J14,1個,2圈)的松動狀態進行識別,識別結果如圖6所示。

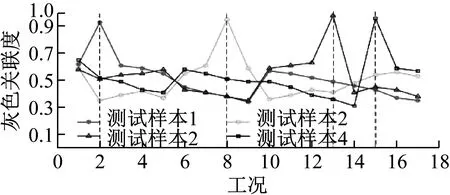
圖6 松動狀態識別結果Fig.6 Loose state identification results

由圖6可知,測試樣本1,2,3,4與17個參考狀態的灰色關聯度,由灰色關聯診斷依據可知,測試樣本1處于工況2,測試樣本2處于工況8,測試樣本3處于工況13,測試樣本4處于工況15,識別結果完全正確。

3.2 真實輸電桿塔試驗

研究桿塔松動識別的最終目的是應用,因此在真實的輸電桿塔上驗證所提出的方法是必要的。試驗日期為2021-11-21,天氣狀況良好,風速6～8 m/s,試驗對象為某個非在役輸電桿塔。

對于實際結構來說,不同連接點受力不同,發生松動的幾率也不同,測量裝置只需要布置在容易發生松動的位置,即測點的布置數量和位置根據結構的受力分析和動力響應分析結果確定。文獻[25]通過對輸電桿塔塔線體系在風荷載作用下的動力響應分析,發現桿塔的危險部位位于塔體下端的結構連接處,如圖7(a)所示,在這一區域,應力和軸向力都處于較高值,因此最容易發生松動。將MEMS監測裝置安裝在該區域的某個節點處,實時獲取桿塔的振動信號,安裝示意圖如圖7(b)所示。

圖7 真實桿塔試驗Fig.7 Real test of tower

根據表3設計的松動狀態,對測量點所在層的四個節點進行試驗,桿塔連接結構和松動螺栓如圖7(c)與圖7(d)所示,最終得到17種工況下的振動信號。利用本文提出的方法對測試樣本1(J11,0個,0圈),測試樣本2(J12,1個,2圈),測試樣本3(J13,1個,1圈),測試樣本4(J14,2個,2圈)進行識別,識別結果如圖8所示。

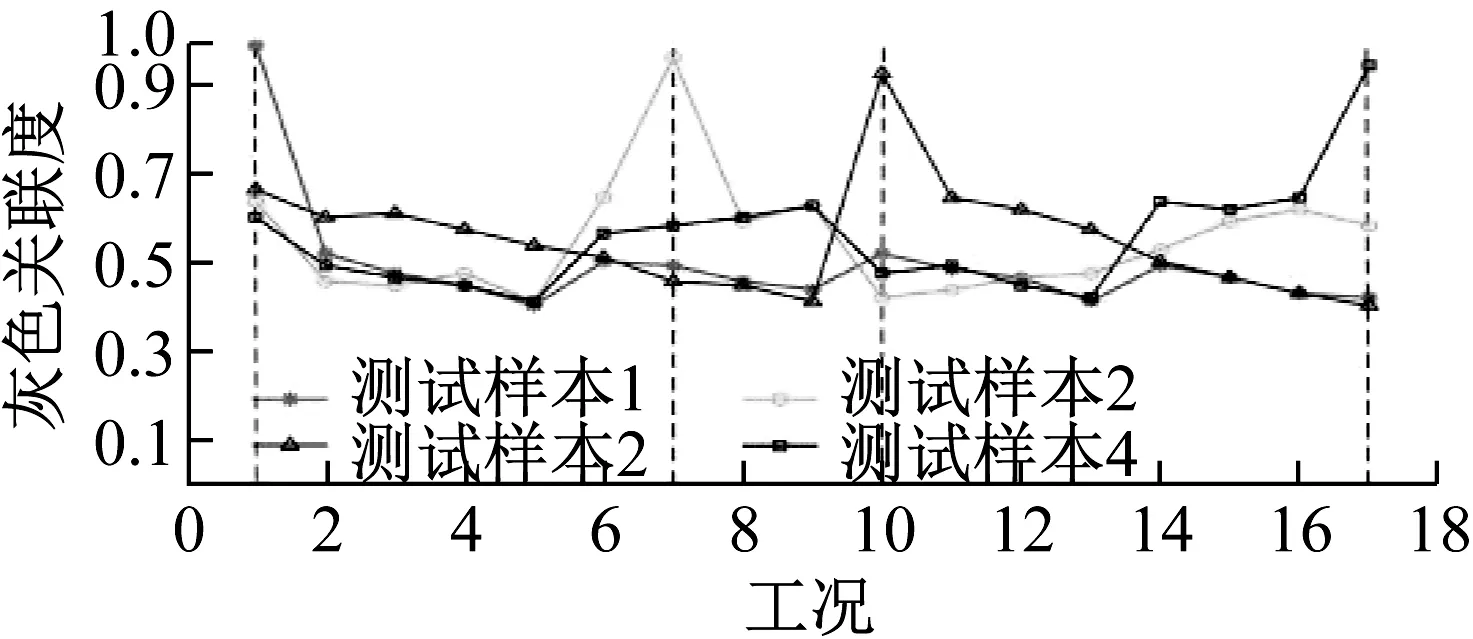
圖8 真實桿塔試驗Fig.8 Real test of tower

由圖8可知,測試樣本1,2,3,4與17個參考狀態的灰色關聯度,由灰色關聯診斷依據可知,測試樣本1處于工況1,測試樣本2處于工況7,測試樣本3處于工況10,測試樣本4處于工況17,識別結果完全正確。

4 結 論

針對環境激勵下輸電桿塔結構松動狀態的識別問題,提出一種基于DMD分析和灰色關聯分析的識別方法。通過模型桿塔與真實桿塔的試驗分析,得出以下結論:

(1) 采用MEMS慣性測量系統測量六自由度的加速度信號,避免了單一方向無法分辨不同松動狀態的問題。

(2) 本文提出的SHDMD算法可以從環境激勵下的桿塔振動響應中得到真實模態,保證作為松動特征的方向振型是真實的,試驗結果表明通過該方法識別的模態結果準確。

(3) 灰色關聯檢測模型通過將待檢測狀態的方向振型與不同松動程度的方向振型進行灰色關聯分析,判斷桿塔結構當前的松動狀態。

試驗結果表明,本文所提出的方法能夠有效識別輸電桿塔的松動節點和松動程度,且有較高的識別率,為輸電桿塔狀態監測提供更準確的參考,對輸電桿塔松動狀態提供預警,避免造成更大的危害。