Q355鋼板對接接頭裂紋擴展所致焊接殘余應力重分布研究

古松，林曉宇，顧穎*，趙亞杰，孔超，任松波

鋼鐵成形

Q355鋼板對接接頭裂紋擴展所致焊接殘余應力重分布研究

古松1，林曉宇1，顧穎1*，趙亞杰2，孔超1，任松波1

（1.西南科技大學 土木工程與建筑學院，四川 綿陽 621010； 2.四川省交通勘察設計研究院，成都 620017）

定量研究裂紋擴展導致的焊接殘余應力重分布效應，得到殘余應力隨裂紋擴展的變化規律。首先采用盲孔法測試了Q355鋼板對接接頭的初始殘余應力；其次利用線切割技術模擬了平行以及垂直于焊縫的裂紋擴展情況，并測試了裂紋擴展導致的殘余應力變化量；最后根據測試數據提出了殘余應力釋放量Δ與裂紋長度之間的函數關系式，進一步得到了基于裂紋擴展的應力重分布計算公式。Q355鋼板對接焊的焊縫區縱向（沿焊縫方向）存在較大的殘余拉應力，拉應力峰值出現在焊趾處，為屈服強度的1.13倍。焊縫區橫向存在梯度較大、拉壓交替變化的殘余應力，壓應力峰值出現在焊趾處，大小為52.6 MPa，拉應力峰值出現在距焊縫中心線17 mm處，大小為63.5 MPa。裂紋擴展能顯著釋放殘余拉應力：裂紋沿焊縫中心擴展，橫向殘余拉應力峰值降低了45.8%；裂紋沿垂直于焊縫方向擴展，焊趾處的拉應力峰值降低了63.3%。裂紋擴展會顯著影響焊接構件的殘余應力分布，根據實測數據提出的裂紋擴展應力重分布計算公式能夠較好地反映殘余應力重分布情況。

焊接殘余應力；裂紋擴展；應力釋放；應力重分布；試驗測試

陳文汨等[11]采用盲孔法實測了里海型拘束焊接試板的殘余應力，發現近焊縫區存在高殘余拉應力。楊俊芬等[12]研究表明，Q690焊接高強鋼管焊縫區的縱向殘余拉應力峰值達到了鋼材的屈服強度。Fisher[13]進行了大尺寸焊接構件的疲勞試驗，研究發現，焊接殘余拉應力是導致構件疲勞強度降低的主要因素。瞿偉廉等[14]通過理論計算對比發現，裂紋擴展導致的殘余拉應力重分布會減緩裂紋的擴展速率。為進一步探究裂紋擴展對焊接殘余應力重分布的影響，Liljedahl等[15]采用中子衍射法測量了2024-T3鋁合金板對接焊垂直裂紋擴展對試件縱向殘余應力重分布的影響。李良碧等[16]通過數值模擬的方式，分析了Q345鋼板對接焊中心裂紋擴展時殘余應力的重分布情況。王強等[17-18]實測了10Ni5CrMoV高強鋼板對接焊垂直裂紋擴展時的殘余應力重分布情況。

上述研究[13-18]均采用數值模擬或試驗測試的方式，對裂紋擴展所致殘余應力的重分布情況進行了分析，但仍存在一些不足：一方面，現有研究多集中在與焊縫垂直的裂紋擴展導致的應力重分布研究，有關平行于焊縫的裂紋研究相對較少，而現實中，裂紋沿焊縫方向擴展，尤其是沿焊趾或焊根方向擴展的現象更為普遍；另一方面，鮮有基于實測數據研究裂紋擴展導致的構件應力重分布效應。

針對上述問題，本文以Q355鋼板對接焊為例，首先采用盲孔法實測了焊接試件的初始焊接殘余應力，其次采用線切割技術預制裂紋并模擬其擴展過程，分別模擬了平行于焊縫的中心裂紋與垂直于焊縫的垂直裂紋的擴展情況，得到了在2種典型裂紋擴展過程中試件殘余應力的釋放量。最后分析了由裂紋擴展引起的殘余應力重分布情況，提出了殘余應力釋放量?與裂紋長度的函數關系式，進一步得到了隨裂紋擴展的重分布應力公式。

1 試件設計

本試驗共制作了3個試件，分別編號為P1、P2、P3，其焊接工藝參數如表1所示，試件由2塊尺寸為800 mm×200 mm×8 mm的Q355鋼板焊接而成，如圖1所示。3個試件均借助焊接機器人進行焊接，從而確保3個試件焊接殘余應力的大小與分布情況相同。焊接時，母材開25°的V形坡口，采用焊接質量較好且速度較快的CO2氣體保護焊將2塊鋼板對接在一起。為防止自動焊時發生燒穿現象，焊接分2次完成，即先在陶瓷襯墊上對接頭坡口進行一道打底焊，完成后再進行蓋面焊。

表1 焊接工藝參數

圖1 試件示意圖

2 焊接殘余應力測試

本研究采用盲孔法，依據GB/T 31310—2014《金屬材料殘余應力測定鉆孔應變法》測試焊件的初始殘余應力。盲孔法的原理如下：在構件表面鉆一小孔（直徑為0.8～4.8 mm），然后測量鉆孔所釋放的應變進而推算殘余應力。按照圖2所示的測試應變布置方式設置應變花，其中1#～3#敏感柵測試的應變分別為1、2、3，根據線彈性理論，測試的殘余應力σ（=1、2）及應力方向角的計算分別如式（1）和式（2）所示。

式中：、為求解應力的關鍵性參數，根據國標，可由數值模擬或試驗標定的方式確定。本研究測試試件為P1，鉆孔的孔徑2=1.5 mm，孔深=2 mm。

鉆孔會導致應力集中，高應力狀態會導致孔邊產生塑性變形從而影響測試精度。本研究依據GB/T31310—2014，通過數值模擬對不同應力水平下的、系數進行標定[19]，以降低塑性應變對測試精度的影響。

NB-IOT模組選用上海移遠公司的BC95-B5模塊，工作電壓為3.1～4.2 V，典型值為3.6 V，與主控芯片USART2連接，該模組支持UDP和COAP協議，使用中國電信的NB卡，通過發送AT指令來實現模組的工作狀態查詢、與服務器進行數據交互等功能。該模組具有CONNECT，IDLE和PSM 3種工作模式，通過切換工作模式能夠大大降低功耗，IDLE狀態下電流為6 mA，PSM狀態下電流僅為5 uA。

圖2 殘余應力測試應變布置示意圖

有研究表明[19]，焊接殘余應力在焊縫的起弧與熄弧段較小，在焊縫中間段達到最大值且應力變化趨于穩定，近焊縫區的殘余拉應力峰值可能超過鋼材的屈服強度，隨著與焊縫距離的增大，拉應力迅速衰減。根據焊接殘余應力分布特征，試驗選取焊縫中間段200 mm范圍內作為殘余應力測試區域，在測試區內測量縱向（方向）與橫向（方向）的焊接殘余應力。

在進行盲孔法多點測量時，孔與孔的間距需大于15倍孔徑[20]，為方便應變片粘貼與接線操作，取測點間距為30 mm。但單條測點間距30 mm的路徑無法準確反映殘余應力的分布情況，根據焊縫中間段應力均勻化的特征，在試件P1中間段200 mm范圍內設置L1～L8共8條路徑對測點進行加密，各路徑測點位置如圖3所示。由于無法在焊縫上粘貼應變片，因此粘貼在距焊縫最近的焊趾處，測得最近測點距離焊縫中心12 mm。

圖3 測點布置圖

基于熱彈塑性有限元法，采用ANSYS軟件，進行了試件初始焊接殘余應力數值模擬。有限元模型坐標系原點位于起弧點，方向為焊接熱源前進方向。焊接溫度場模擬采用Solid70熱分析單元，選用雙橢球熱源模型模擬焊接熱源，并采用“生死單元”模擬焊接熔敷金屬的填充過程，溫度場邊界條件包括環境溫度、輻射傳熱與試件表面對流換熱[7]。基于溫度場分析結果，采用“熱-力耦合”分析將Solid70熱分析單元轉換為Solid185力學分析單元，將溫度場分析結果作為荷載施加于有限元模型，邊界條件定義如圖4所示，計算得到了試件殘余應力大小與分布情況。

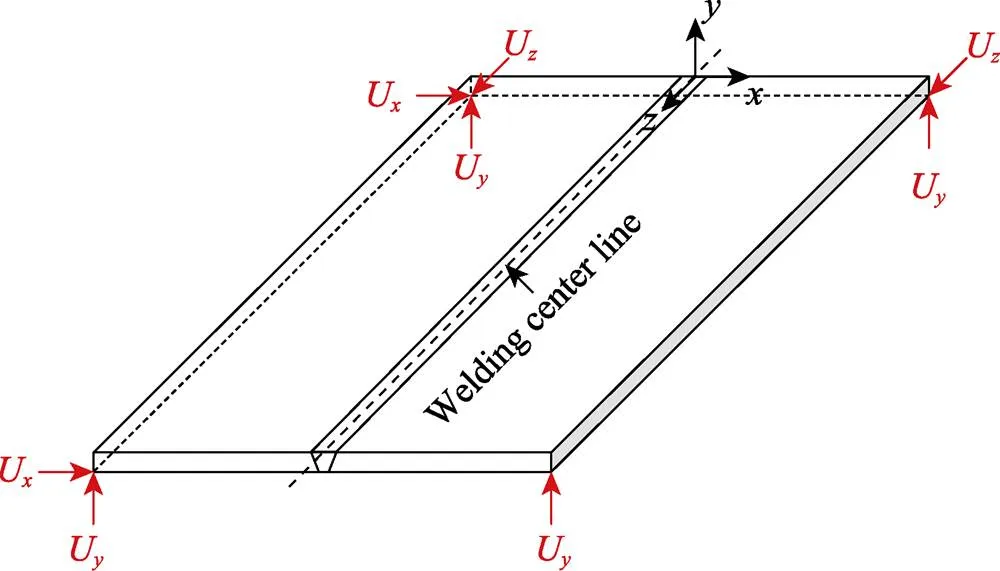
圖4 力學分析邊界條件

模擬結果與實測結果如圖5所示。可以看出，實測結果與模擬結果較為吻合。測試數據顯示，在距焊縫中心29 mm范圍內，縱向殘余應力以拉應力為主，拉應力峰值為401.1 MPa，出現在焊趾處，超出了Q355鋼材的屈服強度。在距中心線約30 mm處，縱向殘余應力轉變為壓應力，并在43 mm處達到壓應力峰值66.8 MPa，這一結果與文獻[21-23]中實測縱向殘余應力分布結果基本相似。橫向殘余應力在焊縫區的應力梯度較大，實測壓應力峰值為52.6 MPa，仍出現在焊趾處，隨后轉變為46.7 MPa的拉應力，并在距焊縫中心17 mm處達到拉應力峰值63.5 MPa。對比Peri?等[22]和Banik等[23]研究中橫向殘余應力的測試結果可知，由于采用的焊接工藝、鋼板尺寸、測點數量均有不同，橫向殘余應力峰值大小與出現位置相差較大，但變化趨勢基本相同，即靠近焊縫區域存在較大壓應力，隨后迅速轉變為拉應力，再緩慢減小至0 MPa。

圖5 試件初始殘余應力分布圖

3 裂紋擴展釋放應力測試

受初始缺陷的影響，焊接結構在循環荷載作用下易萌生和擴展疲勞裂紋。裂紋擴展會釋放材料內應力，導致焊接殘余應力重分布。本試驗利用線切割技術沿設定路徑切割細縫，以模擬疲勞裂紋的萌生與擴展（圖6）。試驗模擬了典型的中心裂紋與垂直裂紋。其中中心裂紋長度為100 mm，采用試件P2模擬，切割時測量垂直于焊縫路徑Path 1上的橫向殘余應力變化量Δσ，如圖7a所示；垂直裂紋長度為48 mm，采用試件P3模擬，切割時測量垂直于焊縫路徑Path 2上的縱向殘余應力變化量Δσ，如圖7b所示。采用小型聯排應變片測量應力變化量，應變柵尺寸為1 mm×1.5 mm，4個一排，間距為5 mm。距焊縫最近的測點位于焊趾處，距離焊縫中心線12.5 mm。

圖6 裂紋擴展試驗

圖7 裂紋與測試路徑示意圖

3.1 中心裂紋

中心裂紋每擴展10 mm記錄一次應力變化。中心裂紋擴展時，P2試件Path 1路徑上的橫向應力變化量Δσ如圖8所示。可以看出，在裂紋擴展初期（裂紋長度≤30 mm），由于裂紋距離測點較遠，裂紋擴展所釋放的應力Δσ較小。當裂紋擴展至40 mm時，焊趾處Δσ出現明顯增長。當裂紋擴展至50 mm時，焊趾處釋放應力為20.5 MPa，此時裂紋尖端剛好達到路徑Path 1的延長線上。當裂紋擴展至60 mm時，焊趾處釋放應力為26.9 MPa，此后隨裂紋的擴展，焊趾處應力釋放速率不斷減小。當裂紋擴展至100 mm時，焊趾處釋放的應力達到峰值34.3 MPa。而在距焊縫50 mm以外區域，Δσ很小，基本維持在±5.0 MPa以內。

3.2 垂直裂紋

垂直裂紋由焊縫中心線向兩側擴展。垂直裂紋擴展時，P3試件路徑Path 2上的縱向應力變化量Δσ如圖9所示。可以看出，一旦垂直焊縫的裂紋開始擴展，焊趾處（=12.5 mm）就有明顯的應力釋放。當裂紋擴展至8 mm時，雖然裂紋仍在焊縫內，但兩側鋼板焊趾處釋放的應力達到約50 MPa。當裂紋擴展至16 mm時，焊趾處Δσ達到89.0 MPa，而后隨著裂紋的擴展，應力釋放速率不斷減小。當裂紋擴展至25 mm時，裂紋尖端恰好位于焊趾處，隨后繼續擴展直至48 mm時停止。停止時，兩側鋼板釋放的殘余應力達到峰值237.5 MPa和216.1 MPa。從整體變化趨勢看，焊縫兩側的應力變化基本對稱。距焊縫中心40 mm范圍內的應力釋放顯著，40 mm外的應力變化幅度較小，有微小的壓應力產生。

圖9 P3試件應力變化

4 結果與分析

4.1 焊接殘余應力重分布

由于裂紋的擴展，存在于材料內部的焊接殘余應力將發生重分布。當前，已經采用盲孔法測得了裂紋擴展前的焊接殘余應力ini，也通過應變片測得了裂紋擴展所釋放的應力Δ，ini與Δ間的差值就是裂紋擴展后的重分布應力re，如式（3）所示

2種裂紋完全擴展后，焊接殘余應力的重分布情況如圖10所示。從圖10a可以看出，裂紋沿焊縫中心擴展使焊趾處的橫向殘余壓應力增大，達到37.3 MPa，相應地，距焊縫中心線18 mm處的拉應力峰值降低了45.8%。

裂紋沿垂直于焊縫的方向擴展會極大地釋放縱向殘余應力，尤其在近縫區約25 mm范圍內，該區域的應力會隨著裂紋的擴展而顯著減小。然而，釋放后的殘余應力仍處于較高水平，拉應力峰值仍有158.8 MPa，接近屈服強度的45%。在距焊縫中心32.5 mm處，縱向殘余壓應力在起裂前小于50 MPa，在裂紋擴展后，焊縫兩側壓應力分別增大到113.4 MPa和97.6 MPa。

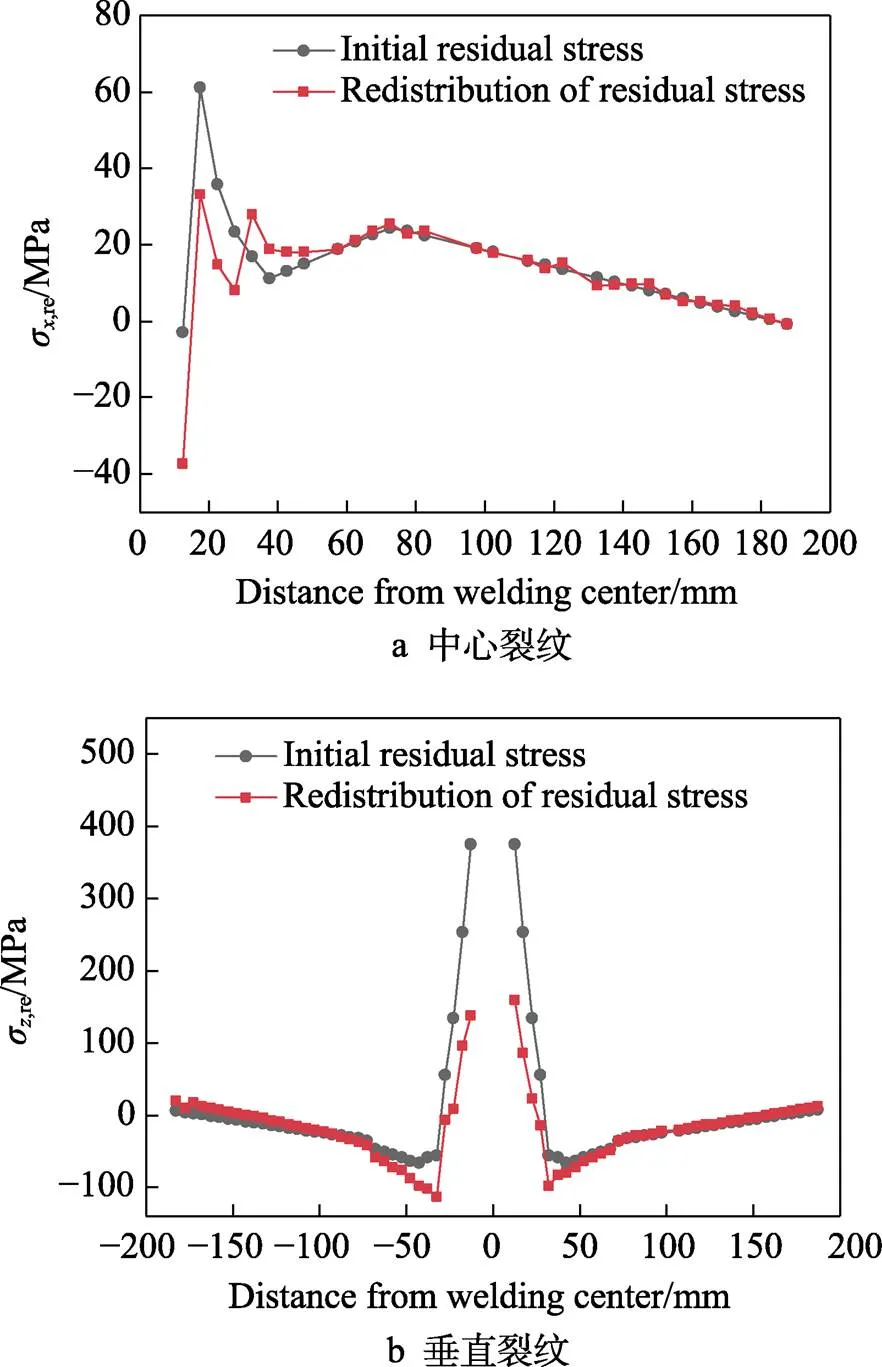
圖10 殘余應力重分布

4.2 隨裂紋擴展的重分布應力公式

試驗結果表明，裂紋沿垂直于焊縫的方向擴展會顯著釋放縱向殘余應力，應力釋放量表現出較強的規律性，可通過式（4）所定義的函數關系來表示，殘余應力釋放量與裂紋長度關系曲線如圖11所示。可以看出，該函數與測試結果匹配較好，符合殘余應力釋放規律。

式中：Δσ()為縱向殘余應力變化值；0為焊縫中心線處的最大殘余應力；為距焊縫中心線距離；為裂紋所在一側鋼板平行于裂紋方向的長度；=/max，其中為裂紋長度，max為裂紋擴展的最大長度；()與()為采用多項式分布擬合的函數（相關系數2分別為0.998 5與0.943 6），如式（5）所示。

結合Tada等[24]和Terada[25]給出的殘余應力分布函數與式（3），可以得到殘余應力σ,re隨垂直裂紋擴展長度的應力重分布計算公式，如式（6）所示。

式中：σ,re為縱向重分布應力；=/，其中為特征長度，定義為從焊縫中心線到初始殘余應力由拉轉變為壓處的距離。

不同裂紋擴展長度的重分布應力實測值與式（6）計算值的對比結果如圖12所示。可以看出，在距焊縫中心40 mm范圍內，式（6）計算的重分布應力與實測值基本吻合，距焊縫中心40 mm處的殘余應力分布受裂紋擴展影響較小，重分布應力無明顯變化，式（6）的計算結果也能體現出這一規律，因此該計算公式能夠較好地反映試驗情況。

圖12 應力重分布實測值與計算值

5 結論

進行了裂紋擴展所致焊接殘余應力重分布的試驗研究，得出如下結論：

1）Q355鋼板對接焊在焊縫區存在較大的縱向殘余拉應力，拉應力峰值高達1.13倍屈服強度，且出現在焊趾處。橫向殘余應力在焊縫區的應力梯度較大，呈拉壓交替變化，壓應力峰值為52.6 MPa，出現在焊趾處，拉應力峰值為63.5 MPa，出現在距焊縫中心17 mm處。

2）裂紋沿焊縫中心擴展使橫向殘余拉應力峰值由61.1 MPa降低至33.1 MPa。

3）裂紋沿垂直于焊縫方向擴展，在焊趾處釋放了大量的縱向殘余應力，但釋放后的殘余應力仍較大，拉應力峰值仍有158.8 MPa，接近屈服強度的45%。

[1] 陳勇, 徐育烺, 楊海波, 等. 304不銹鋼薄壁管件縱縫焊接接頭殘余應力數值模擬研究[J]. 精密成形工程, 2023, 15(3): 155-163. CHEN Yong, XU Yu-lang, YANG Hai-bo, et al. Numerical Simulation of Residual Stress in Longitudinal Welded Joint of 304 Stainless Steel Thin-walled Pipes[J]. Journal of Netshape Forming Engineering, 2023, 15(3): 155-163.

[2] CHANG P H, TENG T L. Numerical and Experimental Investigations on The Residual Stresses of The Butt-Welded Joints[J]. Computational Materials Science, 2004, 29(4): 511-522.

[3] GUO W, FRANCIS J A, LI L, et al. Residual Stress Distributions in Laser and Gas-Metal-Arc Welded High-Strength Steel Plates[J]. Materials Science and Technology, 2016, 32(14): 1449-1461.

[4] FUKUDA S. Analysis of Crack Propagation in Residual Stress Field Using Computer Algebra[J]. Nuclear Engineering and Design, 1989, 111(1): 21-25.

[5] 張紅衛, 桂良進, 范子杰. 焊接殘余應力對橋殼疲勞壽命的影響研究[J]. 機械工程學報, 2022, 58(24): 102-110. ZHANG Hong-wei, GUI Liang-jin, FAN Zi-jie. Fatigue Life Prediction and Experiment of an Axle Housing Considering Welding Residual Stresses[J]. Journal of Mechanical Engineering, 2022, 58(24): 102-110.

[6] PERI? M, TONKOVI? Z, RODI? A, et al. Numerical Analysis and Experimental Investigation of Welding Residual Stresses and Distortions in a T-Joint Fillet Weld[J]. Materials & Design, 2014, 53: 1052-1063.

[7] 顧穎, 馮倩, 任松波, 等. 焊接殘余應力對對接接頭疲勞裂紋擴展的影響[J]. 鐵道科學與工程學報, 2021, 18(10): 2752-2760. GU Ying, FENG Qian, REN Song-bo, et al. Effects of Welding Residual Stresses on Fatigue Crack Growth Behavior of Butt Joint[J]. Journal of Railway Science and Engineering, 2021, 18(10): 2752-2760.

[8] 朱林, 賈民平, 馮月貴, 等. 考慮殘余應力重分布情況下的裂紋擴展預測研究[J]. 機械工程學報, 2017, 53(8): 43-49. ZHU Lin, JIA Min-ping, FENG Yue-gui, et al. Prediction Study of the Crack Propagation with Consideration of the Residual Stress Redistribution[J]. Journal of Mechanical Engineering, 2017, 53(8): 43-49.

[9] SUTTON M A, REYNOLDS A P, GE Y Z, et al. Limited Weld Residual Stress Measurements in Fatigue Crack Propagation Part Ⅱ Fem-Based Fatigue Crack Propagation with Complete Residual Stress Fields[J]. Fatigue Fracture of Engineering Materials Structures, 2006, 29(7): 537-545.

[10] 吳圣川, 李存海, 張文, 等. 金屬材料疲勞裂紋擴展機制及模型的研究進展[J]. 固體力學學報, 2019, 40(6): 489-538. WU Sheng-chuan, LI Cun-hai, ZHANG Wen, et al. Recent Research Progress on Mechanisms and Models of Fatigue Crack Growth for Metallic Materials[J]. Chinese Journal of Solid Mechanics, 2019, 40(6): 489-538.

[11] 陳文汨, 張利, 金立業, 等. 焊接殘余應力的分布和焊后熱處理的應力松弛作用[J]. 金屬熱處理, 2002(2): 30-32. CHEN Wen-mi, ZHANG Li, JIN Li-ye, et al. Distributions of Residual Welding Stress and Effect of Post-Weld Heat Treatment on Its Relaxation[J]. Heat Treatment of Metals, 2002(2): 30-32.

[12] 楊俊芬, 李淵, 彭奕亮. Q690高強鋼管焊接殘余應力數值模擬[J]. 工程力學, 2014, 31(10): 108-115. YANG Jun-fen, LI Yuan, PENG Yi-liang. Numerical Analysis on Welding Residual Stress in Q690 High-Strength Steel Pipe[J]. Engineering Mechanics, 2014, 31(10): 108-115.

[13] FISHER J W. Improved Performance Through Large Scale Dynamic Testing of Structures[C]// IIW International Conference on Performance of Dynamically Loaded Welded Structures, 1997: 1-21.

[14] 瞿偉廉, 何杰, 陳波. 對接焊縫殘余應力對疲勞裂紋擴展的影響[J]. 武漢理工大學學報, 2009, 31(2): 116-119. QU Wei-lian, HE Jie, CHEN Bo. Influences of Welding Residual Stresses on Fatigue Crack Growth of Butt Weld Plate[J]. Journal of Wuhan University of Technology, 2009, 31(2): 116-119.

[15] LILJEDAHL C, ZANELLATO O, FITZPATRICK M E, et al. The Effect of Weld Residual Stresses and Their Re-Distribution with Crack Growth During Fatigue under Constant Amplitude Loading[J]. International Journal of Fatigue, 2010, 32(4): 735-743.

[16] 李良碧, 張沛心, 周宏. 平板焊接接頭裂紋擴展中殘余應力重分布的數值模擬[J]. 電焊機, 2015, 45(8): 90-96. LI Liang-bi, ZHANG Pei-xin, ZHOU Hong. Numerical Simulation of Redistribution of Residual Stress in The Crack Propagation of Plate Butt-Welded Joint[J]. Electric Welding Machine, 2015, 45(8): 90-96.

[17] 王強, 閆忠杰, 劉雪松, 等. 疲勞裂紋擴展過程中焊接殘余應力重分布測試[J]. 焊接學報, 2019, 40(7): 139-142. WANG Qiang, YAN Zhou-jie, LIU Xue-song, et al. A Novel Method for Evaluation of Welding Residual Stress Redistribution during Fatigue Crack Growth[J]. Transactions of the China Welding Institution, 2019, 40(7): 139-142.

[18] WANG Q, LIU X S, WANG P, et al. Numerical Simulation of Residual Stress in 10Ni5CrMoV Steel Weldments[J]. Journal of Materials Processing Technology, 2017, 240: 77-86.

[19] 顧穎. U肋加勁鋼橋面板焊接殘余應力與變形研究[D]. 成都: 西南交通大學, 2016. GU Ying. Research on Welding Residual Stresses and Distortions in Steel Bridge Decks Stiffened with U-Shaped Ribs[D]. Chengdu: Southwest Jiaotong University, 2016.

[20] 金屬材料殘余應力測定鉆孔應變法: GB/T 31310- 2014[S]. Metallic Material-Determination of Residual Stress- Hole Drilling Strain-Gauge Method: GB/T 31310-2014[S].

[21] 黃永輝, 王榮輝, 傅繼陽, 等. 平板焊接接頭縱向殘余應力修正估算公式[J]. 工程力學, 2014, 31(6): 218-225. HUANG Yong-hui, WANG Rong-hui, FU Ji-yang, et al. Modified Estimation Formula of Longitudinal Residual Stress for Flat Plate Welding Joint[J]. Engineering Mechanics, 2014, 31(6): 218-225.

[22] PERI? M, GARA?I? I, TONKOVI? Z, et al. Numerical Prediction and Experimental Validation of Temperature and Residual Stress Distributions in Buried-Arc Welded Thick Plates[J]. International Journal of Energy Research, 2019, 43(8): 3590-3600.

[23] BANIK S D, KUMAR S, SINGH P K, et al. Distortion and Residual Stresses in Thick Plate Weld Joint of Austenitic Stainless Steel: Experiments and Analysis[J]. Journal of Materials Processing Technology, 2021, 289: 116944.

[24] TADA H, PARIS P C. The Stress Intensity Factor for a Crack Perpendicular to the Welding Bead[J]. International Journal of Fracture, 1983, 21(4): 279-284.

[25] TERADA H. Stress Intensity Factor Analysis and Fatigue Behavior of a Crack in the Residual Stress Field of Welding[J]. Fatigue of Aircraft Structures, 2011(1): 5-15.

Redistribution of Welding Residual Stress Caused by Crack Propagation in Butt Joint of Q355 Steel Plate

GU Song1, LIN Xiao-yu1, GU Ying1*, ZHAO Ya-jie2, KONG Chao1, REN Song-bo1

(1. School of Civil Engineering and Architecture, Southwest University of Science and Technology, Sichuan Mianyang 621010, China; 2. Sichuan Communication Surveying Design Institute Co., Ltd., Chengdu 620017, China)

The work aims to quantitatively study the redistribution effect of welding residual stress caused by crack propagation, and obtain the variation law of residual stress with crack propagation. First, the initial residual stress of the Q355 steel plate butt joint was tested through the blind hole method. Then, the crack propagation parallel and perpendicular to the weld seam was simulated with the wire-cutting technology, and the changes in residual stress caused by crack propagation were measured. Finally, based on the test data, a functional relationship between the residual stress release amount Δand the crack lengthwas proposed, and further, a calculation formula for stress redistribution with crack propagation was derived. The results showed that: in the weld zone of the Q355 steel plate butt joint, there was a significant longitudinal residual tensile stress (along the direction of the weld seam), with the peak tensile stress occurring at the weld toe, reaching up to 1.13 times the yield strength. There was also a large gradient and alternating tensile-compressive residual stress in the transverse direction of the weld zone. The peak compressive stress appeared at the weld toe, measuring 52.6 MPa, while the peak tensile stress occurred at a distance of 17 mm from the center line of the weld seam, measuring 63.5 MPa. Crack propagation resulted in a significant release of residual tensile stress. When the crack propagated along the center line of the weld seam, the peak transverse residual tensile stress decreased by 45.8%. When the crack propagated perpendicular to the weld seam, the peak tensile stress at the weld toe decreased by 63.3%. To sum up, the propagation of cracks significantly affects the residual stress distribution in welded components. The crack propagation stress redistribution calculation formula proposed based on the measured data can effectively reflect the redistribution of residual stress.

residual welding stress; crack propagation; stress release; stress redistribution; experimental test

10.3969/j.issn.1674-6457.2023.010.018

TG405；U441.4

A

1674-6457(2023)010-0152-08

2023-04-26

2023-04-26

國家自然科學基金（51708467，52108385）

The National Natural Science Foundation of China (51708467, 52108385)

古松, 林曉宇, 顧穎, 等. Q355鋼板對接接頭裂紋擴展所致焊接殘余應力重分布研究[J]. 精密成形工程, 2023, 15(10): 152-159.

GU Song, LIN Xiao-yu, GU Ying, et al. Redistribution of Welding Residual Stress Caused by Crack Propagation in Butt Joint of Q355 Steel Plate[J]. Journal of Netshape Forming Engineering, 2023, 15(10): 152-159.

責任編輯：蔣紅晨