空間方向關系定性推理技術研究進展

王淼 方振西 王曉桐 李松 郝忠孝

摘 要：空間方向關系是空間認知中的一個基本概念，在空間數據庫、人工智能、機器人等領域發揮著極其重要的作用。隨著空間方向關系應用的不斷深入，空間方向關系定性推理受到了廣泛關注，逐漸成為研究的熱點。為了更進一步地介紹和挖掘空間方向關系推理技術的研究現狀，首先，針對現有的推理模型進行詳細梳理和總結，對各類模型進行比較和分析，指出了各種模型的特性及適用范圍；其次，從二維、三維及不確定性空間對象方向關系的復合、反關系推理、一致性檢驗以及結合多種空間信息的組合推理等幾個方面對空間方向關系推理相關工作進行了系統性的闡述和分析；最后，分析了目前所面臨的挑戰并對其未來發展趨勢進行了展望。

關鍵詞：空間方向關系； 復合； 反關系； 一致性檢驗； 組合推理

中圖分類號：TP181?? 文獻標志碼：A

文章編號：1001-3695（2023）09-001-0000-00

doi：10.19734/j.issn.1001-3695.2023.02.0044

Survey of research on qualitative reasoning with spatial direction relations

Wang Miao1， Fang Zhenxi2， Wang Xiaotong3， Li Song4， Hao Zhongxiao4

（1.Schhool of Computer Science， Henan University of Engineering， Zhengzhou 451191， China; 2.School of Computer Science， Zhongyuan University of Technology， Zhengzhou 450007， China; 3.School of Computer Science & Engineering， Central South University， Changsha 410083， China; 4.School of Computer Science & Technology， Harbin University of Science & Technology， Harbin 150080， China）

Abstract：Spatial direction relation is a basic concept in spatial cognition， which plays an important role in the fields of spatial database， artificial intelligence， robot and so on. With the application of spatial direction relation， the qualitative reasoning with spatial direction relations has gradually become a hot issue， which has received a lot of attention. In order to further introduce and explore the research status of qualitative spatial reasoning with directions， firstly， this paper combed and summarized the existing models for reasoning with directions in detail， compared and analyzed all kinds of models， and pointed out the characteristics and the applicable scope of all kinds of models. Then， it systematically surveyed the researches of spatial reasoning with direction relations including composition， inversion， consistence checking with direction relations for two-dimensional， three-dimensional and uncertain objects and the researches of compound spatial reasoning based on direction， topology and distance. Finally， this paper discussed the current challenges and potential development trends.

Key words：spatial direction relation; composition; inverse; consistency checking; compound spatial reasoning

0 引言

空間方向關系作為空間認知和推理的前提，描述了空間對象間的序關系，在空間信息分析與處理領域有著廣泛的應用［1，2］。定性空間推理一直是人工智能領域研究的重要內容，日益成為空間數據庫、地理信息系統、模式識別、圖像處理和機器人等領域的研究熱點和難點，其研究成果廣泛應用于國民經濟和社會發展的諸多領域，如智能交通、空間智能分析處理、防災減災、虛擬空間建模等，無論在理論還是實際應用中都具有重要的意義［3，4］。

隨著GIS應用的不斷深入，空間方向關系受到了廣泛關注，諸多模型相繼被提出［5］，如錐形模型、投影模型、Voronoi圖模型、方向關系矩陣模型、最小外包矩形模型（MBR）等。為了進一步提高模型的精度，減少空間對象自身形狀、大小等因素對描述精度的影響，提出了一些改進模型，如2-D string模型、單方向Voronoi圖模型、方向關系二元組模型、凸殼模型、群組Voronoi圖模型等，目前已形成了較為完備的理論體系，廣泛應用于空間查詢與推理領域［6，7］。空間目標的存在形式除點、線、面外，很多目標還是以群組的形式存在，目前有關群組目標方向關系模型的研究相對滯后。

然而現實世界是三維空間，依據對空間劃分粒度的不同，諸多三維空間方向關系模型相繼被提出。由于三維空間方向關系相對復雜，目前有關三維空間方向關系的研究相對滯后，是近幾年研究的熱點和難點。現實世界中的很多現象復雜多變，受數據采集方式、人們的認識以及GIS 中描述方式的影響，GIS 所描述的空間關系與真實目標間以及與人們認知存在一定的差異，即空間對象的不確定性。目前對不確定方向關系的研究相對薄弱，未來應尋求統一描述精確對象和各種來源的模糊對象的表達與推理模型，以提高對復雜空間對象的分析和處理能力［8］。

隨著空間方向關系應用的不斷深入，人們已不滿足于僅僅對空間方向關系進行簡單的描述和存儲，還要求空間數據庫系統對空間方向關系具有一定的智能預測與分析、推理能力。空間方向關系定性推理的研究主要包括空間方向關系復合、反關系推理及空間方向關系網絡一致性檢驗等。近年來，雖然有諸多空間方向關系表達與推理模型被提出，但由于一些模型的自身缺陷以及對相應的推理技術研究薄弱，導致空間方向關系的推理能力仍很有限，這在一定程度上阻礙了空間方向關系的應用。目前，關于空間方向關系復合及反關系推理的研究主要針對二維和三維空間精確對象，雖然有一些推理方法相繼被提出，但這些工作大多依賴于復雜的推理運算法則和推理運算表。一致性檢驗由于其基礎性、必要性吸引了眾多學者的關注，就一般情況而言，方向關系網絡的一致性檢驗問題是NP完全的，雖然采用的合成運算方法不同，但最終的判定原理大都是基于路徑一致性理論，這些方法普遍復雜且計算量大，處理效率低下，根本無法滿足實際應用需求。目前針對拓撲、方向、距離等單方面空間關系的表達與推理研究相對成熟，然而利用單一空間關系難以對復雜的空間信息進行有效處理，結合多種空間關系的組合表達與推理成為近年來的研究熱點和難點。

總體上看，目前對二維空間研究得較多、對三維空間研究得較少、對精確對象研究得較多、對模糊對象研究得較少，空間方向關系的自動推理能力亟待提高，對三維及模糊空間對象方向關系的復合和反關系推理處理能力仍很欠缺。本文對現有的推理模型進行全面的分析和總結，針對現有的模型進行分析比較，闡明各類模型的特性及適用范圍。依據處理對象的不同，分別從點、線、區域，依據所采用的技術、方法和手段等，針對二維確定及不確定、三維確定及不確定空間方向關系的復合、反關系推理、一致性檢驗及結合多方面空間信息的組合推理等幾個方面闡述了空間方向關系推理領域研究進展，在認真分析、歸納當前工作的基礎上，指明了當前空間方向關系推理模型和推理方法存在的不足和未來發展的方向，為進一步的研究提供借鑒和參考。

1 方向關系模型

1.1 二維空間方向關系模型

二維空間對象方向關系模型日漸趨于完善和成熟，廣泛應用于空間數據查詢與推理。現有的二維空間方向關系模型主要有錐形模型、基于投影的模型、基于Voronoi圖的模型和群組對象方向關系模型等幾類。

1.1.1 錐形模型

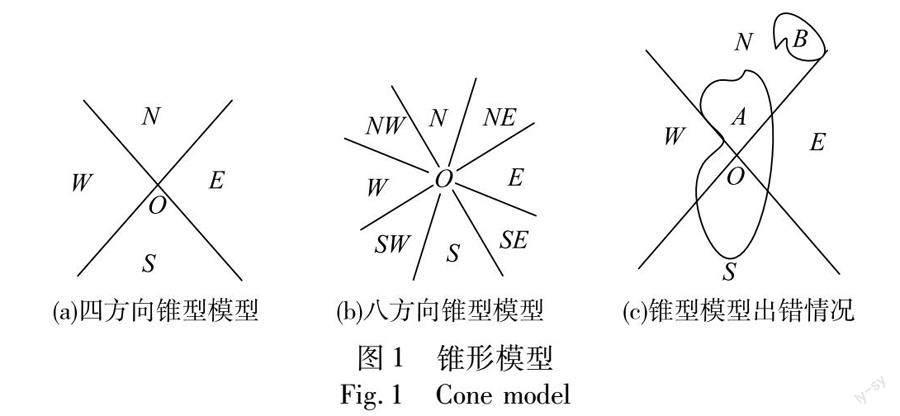
錐形模型將參考對象及其周圍的空間區域劃分為多個方向區域，通過考查目標對象與參考對象方向區域的交集是否為空來描述空間對象間的方向關系。具有代表性的錐形模型有四方向錐形模型和八方向錐形模型，均以某一空間目標為參考目標。四方向錐形模型以東西南北方向線為軸將空間目標及周圍的區域等分成四個方向區域來定義方向關系；八方向錐形模型以東西南北方向線以及四方向錐形模型邊界線為軸，將空間目標及周圍的區域分成八個方向區域定義方向關系，如圖1所示。錐形模型將空間對象抽象為點，易于計算和推理，可塑性強，但描述線對象和面對象時精度不高，比較適合小尺寸空間。由于將空間目標抽象為點，導致計算精度不高且受形狀、大小的影響較大，四方向和八方向錐形模型都存在實際感知的方位關系與模型描述的結果出現偏差。如圖1（c）所示，四方向錐形描述的方向關系為B在A的北方，而實際所感知的方向關系是B在A的東北方。因此，四方向和八方向錐形方向關系模型適合于大尺度空間下距離較遠的空間對象間方向關系的分析和處理。

錐形模型由于將空間目標抽象為點，導致計算精度不高且受形狀和大小的影響較大，無法用于描述線和面等類型的空間對象。許多學者在錐形模型的基礎上進行改進，提出了融入方向關系矩陣的改進錐形模型，較好地顧及了空間對象的形狀、大小和距離對方向關系的影響，提高了表達與推理的精度。

1.1.2 基于投影的模型

基于投影的MBR模型利用最小外包矩形（MBR）近似替代空間對象，能夠區分169種空間關系。該模型一定程度上考慮了空間對象自身形狀和大小帶來的影響，但是當兩個空間目標的MBR相交時，可能導致空間方向關系描述困難，該模型常作為空間目標拓撲關系判定的過濾器。為此，Goyal等人提出了方向關系矩陣模型，利用參考對象的最小外包矩形將空間劃分成九個方向區域，如圖2所示。通過計算主對象B與參考對象A的九個方向區域交集是否為空構造一個矩陣表達空間對象間的方向關系，更符合人類的認知習慣，是目前較為理想的二維區域對象方向關系表達與推理模型。

方向關系的相似性度量在矢量空間數據的檢索［9］、匹配［10］、質量評估［11］、遙感影像檢索［12］及查詢［13～15］等領域發揮著至關重要的作用。為了進一步提高表達與推理的精度，李朋朋等人［16］利用空間方向關系的反關系計算目標對象與參考對象的最小投影矩陣在包含或相交時的方向關系，進一步拓展了方向關系矩陣的應用范圍，相似性計算的結果更準確，但該模型無法描述空間目標相互纏繞的情形。

針對方向關系矩陣模型對同一方向片區方向變化識別能力不足等問題，龔希等人［17］基于格網方向關系矩陣模型，引入對象方向片區質心角度提出了一種基于方向關系二元組的相似性度量方法，該方法可有效識別同一方向片區內的方向變化。宗琴等人［18］優化了復合表達模型的方向關系矩陣，建立了定量的方向關系矩陣，對參考對象的空間區域進一步劃分，降低了參考對象本身形狀因素對參考區域的影響，同時使得目標對象受形狀、大小和距離的影響更小，在處理參考對象與目標對象出現包含與纏繞情形時有著顯著的優勢。

1.1.3 基于Voronoi圖模型

基于Voronoi圖的模型依據空間對象的Voronoi圖與自身的關系來描述空間對象間的方向關系，描述的精度相對較高，但模型計算較為復雜。基于Voronoi圖的空間方向關系形式化描述模型如圖3所示，A為參考目標，B為源目標，實線表示方向Voronoi圖，虛線表示可視區域的Delaunay三角網，該模型不受距離、分辨率等因素的影響，無須區分參考對象和目標對象，同時擯棄了MBR、2D String模型等將空間方向關系單一化的缺陷。

陳超等人［19］利用方向Voronoi圖模型來計算面狀組目標之間的空間方向關系，在一定程度上克服了空間對象自身形狀、大小等因素帶來的影響，但沒有給出相應的推理方法。總體上來說，基于Voronoi圖的模型適合于多種情況下的空間方向關系的描述，精度相對較高但計算復雜，不易于進行形式化推理。

1.1.4 群組模型

空間目標的存在形式除點、線、面外，還以群組的形式存在，群組目標是多個單目標因為形態相似、距離相近、語義相近而組成的一個視覺整體，如道路網、河流網、居民地群等。群組目標空間方向關系受群組目標之間的空間距離、分布范圍、空間形狀和分布密度等因素影響，描述更為復雜，目前有關群組目標空間方向關系表達與推理模型的研究相對滯后［20］，現有模型主要有三類：a）借助凸殼對群組目標方位關系進行研究，將源群組目標轉換為單目標，利用已有單目標空間方向關系模型判斷源目標群和參考目標群之間的方向關系，如圖4所示；b）通過方向Voronoi圖計算群組目標間的方向關系［21］，利用各主方向上Voronoi邊的長度值與Voronoi 邊法線總長度值的百分比描述方向關系，如圖5所示；c）借助Delaunay三角剖分［22］、“剝皮”算法和數學形態學［23］等理論工具對群組目標進行定性描述和計算。

王玉竹等人［24］基于模糊最大隸屬度原則提出了一種改進的群組目標空間方向關系計算模型，該模型很好地顧及了群組目標大小與形狀對空間方向關系的影響，提高了方向關系表達與推理的精度，該模型計算簡單便捷且符合人們的方位認知習慣。為進一步研究多尺度群組之間方向關系相似性度量問題，江坤等人［25］提出了基于錐形模型的面群方向關系表達模型，結合目標大小和目標間的距離給出了兩個面群之間的方向關系表達模型，該模型能夠較準確地計算出多尺度面群之間的方向關系相似度，較好地克服了方向關系矩陣模型在描述群組之間方向關系的弊端。總體上看，目前關于群組目標空間方向關系描述模型的研究尚處于起步階段，無法很好地考慮諸多因素對于群組目標方向關系的影響，群組目標方向關系描述的精度亟待提高。

錐形模型將空間對象抽象為點，易于計算與推理，可塑性強，比較適合小尺寸空間，但由于將空間目標抽象為點，導致計算精度不高且受形狀和大小的影響較大。由于錐形模型無法用于描述線和面等類型的空間對象，許多學者在錐形模型的基礎上進行改進，主要有兩類方法，一類是引入參考對象的最小邊界矩形，另一類是對空間進一步細分，增加主方向關系的數目。二維字符串模型將空間區域按水平和垂直方向投影，較好地描述了二維空間區域對象間的方向關系，適用于多種類型的空間對象，但方向關系的表達較抽象，不夠直觀、不易于理解。

基于投影的模型在一定程度上顧及到空間對象自身形狀和大小對空間方位關系的影響，彌補了錐形模型的不足。方向關系矩陣模型是目前較為理想的二維區域對象間方向關系表達模型，易于計算和進行形式化推理，其有兩大優勢：a）消除在空間方向關系表達時利用近似點或基于坐標投影的方法帶來的大量不合理或者非法結果集的情況；b）不再使用任何過濾算法對結果進行過濾。與其他模型相比，Voronoi圖模型較好地反映了空間對象的大小、形狀和距離等因素對空間方位關系的影響，可以獲得相對準確的空間方位信息，但計算過程復雜、計算量大，不易于進行形式化的推理。

雖然對二維空間對象方向關系推理模型的研究已有不少工作，但描述精度仍有待進一步提高，離基于真實物體的描述仍有較大差距。此外，結合方向關系、距離關系和拓撲關系等多種空間關系的復合表達與推理是未來研究的重點，將致力于尋求統一的表達與推理模型，增強對空間對象的約束，解決現有模型表達與推理精度不高的問題，在二維空間獲得更為精確的空間信息。

1.2 三維空間方向關系表達模型

目前，對二維空間方向關系表達與推理模型的研究相對成熟，但這些模型無法用于處理三維空間方向關系［26］。隨著空間方向關系應用的不斷深入，三維空間方向關系在城市建筑設計［27］、機器人學［28］、圖像處理［29］等諸多領域均有涉及，二維空間方向關系模型無法滿足三維空間應用需求，因此迫切需要對三維空間對象方向關系表達與推理模型進行研究。

目前，有關三維空間方向關系表達與推理的模型主要分為三類：

a）將二維空間方向關系表達模型向三維空間拓展。如圖6所示，將二維雙十字模型向三維空間擴展用來描述三維空間點對象間的方向關系，將三維空間區域細分為75個方向區域，但該模型忽略了空間對象的大小、形狀和內部細節等問題，描述精度不高。王淼等人［30］將方向關系矩陣模型向三維空間擴展提出的3DR27模型如圖7所示，該模型計算簡便，便于進行形式化推理，該模型下基本主方向關系多達38209336種，數量龐大，推理工作復雜繁重。因此，迫切需要對該模型下三維基本主方向關系的復合、反關系推理及三維主方向網絡一致性的自動判定與推理問題進行研究。

b）根據三維空間劃分粒度的不同，眾多學者在3DR27模型的基礎了進行了一系列的改進，依據劃分粒度的不同相繼提出了3DR34［31］、3DR39［32］、3DR44［33］等模型。3DR39模型將三維空間區域進一步細分為39個方向區域，但并未考慮最小外包盒內部方向關系劃分問題，雖在一定程度上提高了表達精度，但推理過程較復雜；3DR34和3DR44模型較好地顧及了參照對象近似最小包圍盒內部的細節方向關系，但3DR44模型對空間的劃分過于復雜，不利于進行形式化推理，且對參考對象大小有著較強的依賴性。基于3DR44模型對空間粒度進一步細分，分別提出了3DR46模型［34］和3DR50模型［35］。3DR46模型將參照對象區域進一步細分為8個方向區域，以描述參考對象最小外包盒內部的細節方向關系，并基于該模型給出了動態方向塊的動態鄰接關系；3DR50模型為適應參考對象大小的變化增加了12個方向區域，改善了3DR44模型對參考對象大小的依賴。

c）結合多種空間信息的復合模型，將方向關系和距離關系相結合提出了3DR39-3d［36］和3DR44-4d［37］模型。3DR39-3d模型能夠描述2 115種方位關系，并給出了該模型下基本主方位關系的反關系推理方法，但無法處理一些較為復雜的三維方向關系的表達和推理；3DR44-4d模型能夠區分與描述目標對象和參照對象位于同一方向塊的空間方向關系，將三維空間細分為158個方向空間塊，可以描述2 158種三維空間方位關系。賈曉晴等人［38］結合錐形模型和定性距離提出了一種3D-ICSRM模型，該模型適用于小比例尺空間下三維空間對象方位關系描述，由于將空間對象抽象成點，表達與推理精度不高。OPRAm模型是一種具有可擴展的點方位關系代數模型，歐陽繼紅等人［39］將其擴展到三維空間，提出了一種三維對象間的相對方位關系3DOPRAm模型，該模型結合角度與距離能夠較精確地表達點對象方向關系，但受空間對象形狀的影響較大。在對上述模型進行對比和分析的基礎上，表1詳細地給出了各種模型的特性及其適用范圍。

目前，三維空間方向關系的研究相對滯后，現有的模型普遍存在描述精度不高或者忽略參考對象內部細節等問題，另外對三維不確定對象間方向關系、三維空間對象鄰近關系的相關研究較少。近年來靜態時空對象、單方面空間信息及二維空間對象方向關系的定性推理研究逐步成熟，但對于運動對象空間關系及三維模糊空間關系推理研究甚少。由于三維空間固有的復雜性，使得有關三維空間方向關系的復合、反關系及一致性檢驗等推理工作研究相對滯后，雖有一些模型被提出，但由于三維空間基本方位關系數目繁多、推理計算復雜、工作量大，若依靠手工推理根本無法滿足實際應用需求，所以迫切需要研究和發展三維空間方向關系的自動推理技術。

1.3 不確定性對象間的方向關系模型

地理信息系統所描述的空間關系與人們所感知的真實空間對象間空間關系存在差異，即空間信息的不確定性［40-41］。現實生活中存在諸多不確定性對象，例如山川、河流、沙漠等，確定性方向關系模型不能直接用來描述具有不確定性邊界的空間對象。因此，需要對不確定性空間對象方向關系表達與推理模型進行研究。

1.3.1 確定性對象方向關系模型的擴展模型

現實生活中人們趨向于用分明區域的方式描述不確定區域間的方向關系。蛋黃模型利用三個謂詞{A，M，N}的不同取值來描述不確定區域間的拓撲關系，三個謂詞依次表示兩個不確定區域的所有可能分明區域對使謂詞成立，存在兩個不確定區域的分明區域對使謂詞成立和不存在兩個不確定區域的分明區域對使謂詞成立，將分明區域看做是不確定區域的一個特例，三個謂詞的取值更符合人們的認知習慣。

為彌補現有的基于寬邊界區域不確定性模型存在的方向關系數目繁多、方向區域劃分不符合人們的認知習慣等問題，相繼提出了不確定性區域間定性方向關系模型和模糊目標的拓撲參考計算模型。不確定性區域間定性方向關系模型減少了方向關系的數目，且更符合人類認知；模糊目標的拓撲參考計算模型進一步綜合模糊參考目標和模糊源目標的模糊隸屬度，建立模糊目標方向關系定性描述模型，有效提高了模糊目標方向關系描述的精度。

Xiang Jun［42］基于角度的模糊隸屬函數提出了一種將錐形模型與方向關系矩陣模型相結合的模糊對象方向關系建模方法，將參考與目標實體分為點與點、點與面、面與面分別進行描述，實體為點與點、點與面時利用錐形模型進行描述，如圖8所示，實體為面與面時利用矩陣模型進行描述。充分結合兩種模型的優點，并將該模型應用于環境監測領域，有效地提高了污染源方位判斷的效率。

1.3.2 基于不確定性集合理論模型

現有的不確定方向關系模型通常將精確對象和模糊對象分裂處理，容易導致結果的不確定性和推理精度的損失。將粗糙集理論引入空間方向關系描述領域，針對空間對象的描述分為四種情況，如圖9所示。基于粗糙集的粗糙可辯性，允許空間方向關系表達存在誤差并能進行近似的推理工作，將模糊對象和精確對象間的方向關系統一描述，不再是割裂的處理。

基于模糊集理論的方向關系模型，雖在一定程度上顧及了人們的認知習慣，但不確定邊界的隸屬函數難以確定，且計算量大。基于點集拓撲的概念對不確定區域進行定義，用區間值表示不確定區域間方向關系的隸屬程度，彌補了處理分明區域時模糊集截集的不足，優勢在于將分明區域看做不確定區域的特例統一處理。

實際應用中含洞的不規則模糊區域以及區域關系普遍存在，而以往的研究大多針對規則的不含洞模糊區域，為此文獻［43，44］基于Vague集對含洞不規則Vague區域和動態Vague區域進行了系統的研究，使其能夠處理復雜的含洞不規則Vague區域關系，并給出了含核Vague域的空間表達以及動態關系鄰接表和動態關系轉變路徑，實現了利用Vague集形式化描述含洞的不規則區域，適用于較為復雜的模糊區域關系。董軼群等人［45］基于寬邊界模型和MBR模型研究了不確定區域間方向關系的表達與推理，擴展了Allen的路徑相容性算法，提出了一種寬邊界方向關系相容性檢測算法。

目前不確定性方向關系的研究雖然取得了一些成果，但起步較晚，相對薄弱，已有的研究大致分為兩類，一是確定性空間對象方向關系模型的擴展模型，二是基于不確定性集合理論模型。具有代表性的擴展模型有錐形模型、蛋黃模型、擴展蛋黃模型、基于Vague集的線性Vague時間段關系模型、周期性雙向疊合Vague時間段關系模型等。具有代表性的基于不確定性集合理論模型有粗糙集模型、模糊集模型、線性Vague時間段關系模型等，粗糙集和模糊集是目前應用比較廣泛的不確定性處理方法。總體上來說，確定性對象方向關系模型的擴展模型描述簡單、易于理解，延伸了確定性方向關系模型的應用范圍，但無法統一處理多種不確定性源的空間對象；粗糙集、模糊集和Vague集利用隸屬度來表示不確定程度，在描述上與現實生活中人們的認知更加接近，但隸屬度函數比較難確定，計算量大，未來應致力于尋找統一的表示與推理模型有效地處理模糊對象間的方位關系，提高對復雜空間對象的分析與處理能力。

2 空間方向關系推理

空間方向關系定性推理的研究主要包括方向關系復合，反關系推理及空間方向關系網絡一致性檢驗等。空間方向關系推理技術作為空間場景相似性評價以及圖像理解等領域的核心技術，在城市管理規劃、市政工程、智能交通等領域有著廣泛的應用［46～48］。例如，在智能交通系統中可利用方向關系復合和反關系推理的結果作為路徑選取的約束條件，減少搜索范圍，提高搜索效率。因此，空間方向關系推理研究具有重要的理論意義和實際應用價值。

2.1 方向關系的復合

空間方向關系復合作為空間方向關系的基本操作，在實際中有著廣泛的應用。空間方向關系復合分為實體論復合和

一致性復合兩種，理論上實體論復合是方向關系復合的標準定義，但在實際生活應用中一致性復合作用更加凸顯。下面將從二維、三維以及不確定空間對象方向關系等三個方面對空間方向關系的復合推理研究進行梳理和分析。

2.1.1 二維空間方向關系復合推理

區間代數理論易于進行形式化的推理，因其良好的計算性質廣泛應用于定性空間推理領域，例如空間關系的復合、反關系推理及網絡一致性檢驗等。下面對區間代數理論進行介紹，分析其特性和優勢以及未來的發展趨勢。

區間代數用于描述兩個有限區間的序關系，根據區間端點間的次序關系定義了13種基本區間關系，即before（b）、meet（m）、overlap（o）、start（s）、during（d）、finish（f）以及它們的反關系bi、mi、oi、si、di、fi和equal（eq），如圖10所示。這13種基本區間關系是唯一的、完備的，即對于任意兩個區間，它們之間的關系必然滿足13種的一種，它在定性空間推理中發揮著極其重要的作用。

矩形代數本質上是將區間代數向二維空間擴展，一個基本的二維代數關系是一個形如（p1，p2）的二元組，其中pi∈{b， m， o， s， d， f， bi， mi， oi， si， di， fi， eq}，i∈{1，2}，且對于任意的二維空間對象a 相對于b滿足代數關系（p1，p2），當且僅當對于任意的i∈{1，2}，ai相對于bi 滿足區間關系pi，其中ai和bi 分別為a和b在兩個維度上的投影。基于矩形代數理論，可建立基于MBR的主方向關系與矩形代數之間的等價聯系，如表2所示。借助二者之間的等價聯系可將基于MBR的主方向關系網絡轉換為等價的矩形代數網絡，利用區間代數的推理運算規則實現基于MBR的主方關系的復合，取反及一致性判定等。

二維基本矩形主方向關系與矩形代數之間存在等價聯系，則三維基本矩形主方向關系與三維代數間也必存在等價聯系。王淼等人［30］提出的3DR27模型易于計算和推理，該模型下216種三維基本矩形主方向關系與三維代數關系之間的等價聯系如圖11所示。因此，可利用二者之間的等價聯系將3DR27模型下三維矩形主方向關系網絡轉換為等價的三維代數網絡，這為利用區間代數在與復合和取反等方面良好的運算特性實現3DR27模型下三維基本主方向的復合、反關系推理及一致性判定等奠定了基礎。

原子方向關系間的復合推理是方向關系推理的基石，基于方向關系矩陣模型的原子方向關系間的復合推理相對完善。基于方向關系矩陣模型的原子主方向關系與基本主方向關系復合方法，其復合操作主要是在Most運算的基礎上進行原子方向關系的復合，但Most運算計算過程復雜。基于方向關系矩陣模型給出的基于一致性復合的推理方法使得原子方向與基本方向關系之間的復合逐步完善，但是該方法不能應用于非連通區域。

傳統的方向關系模型很難同時對點、線、面等物體進行統一的處理。為此，萬靜等人［49］提出了一種基于矩陣的主方向關系推理的方法，針對點、線、面物體分別進行處理。該方法的主要思想是將矩陣分為單元矩陣和多元矩陣，本質上均是對單元矩陣進行計算，在單元矩陣復合時，無須查看推理運算表，提高了運算效率且降低了存儲空間。

Skiadopoulos證明了Goyal等的復合理論是不完善的，從結果的存在性和一致性對該復合理論進行了修正，提出了方向關系矩陣模型下基本主方向關系的復合推理方法［3］，該方法借助36種基本矩形主方向關系的Most運算和推理運算表實現，但Most運算過程較為復雜。歐陽繼紅等人［50］對Skiadopoulos的復合方法進行了改進，簡化了Most運算過程，推理過程更簡便。

為了進一步提高方向關系矩陣模型下主方向關系推理的精度，王淼等人［51］引入了定性直角坐標系的概念，將方向和距離關系有機結合，提出了結合方向關系和距離關系統一的表達與推理模型，定性坐標系對參考對象空間的劃分如圖12所示。該模型充分考慮到空間對象的形狀及空間布局對方向關系的影響和制約，有效地降低了主方向關系推理結果的不確定性，提高了推理的精度。

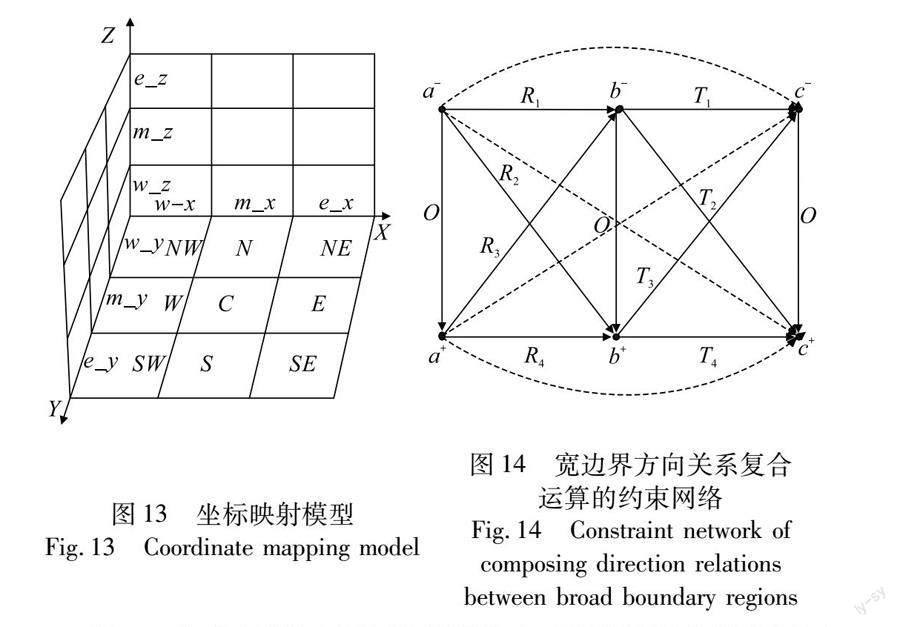
基于真實物體的復雜空間對象方向關系的復合推理研究將真實物體分為兩類，即物體是同胚的、閉合的圓盤狀個體和物體是不相連的、含洞的，如圖13所示。另一類是針對非連通區域對象方向關系復合推理，現有的推理方法大多是基于tile-union運算，將結果中無效的或者不連通的基本主方向關系排除，以提高運算效率。

丹曉飛［52］將錐形模型和投影模型進行結合提出了一種針對點對象的改進模型，該模型將點對象轉換為柵格數據，基于柵格數據的屬性值和方向關系實現空間方位關系的表達與推理，但推理的精度受柵格劃分程度影響較大，且柵格數據量較大，計算復雜。針對點、區域等空間對象方向關系復合推理的研究相對成熟，由于空間對象固有的復雜性，雖有一些模型被提出，但能夠同時處理點、線、面等空間對象的模型甚少，推理能力仍很薄弱；運動是事物的根本屬性，以往的研究大多針對靜態時空對象，針對移動時空對象的研究甚少，是未來研究的重點。隨著空間方位關系應用的不斷深入，對空間方向關系表達與推理的精度提出了新的、更高的要求，迫切需要研究結合多種空間信息的表達與推理模型，使之能夠處理更為復雜的方位關系。此外，現實生活中空間對象還以非連通區域的形式存在，目前對非連通區域對象方位關系復合推理的研究相對薄弱，是未來研究的重點。

2.1.2 三維空間方向關系復合推理

三維空間方向關系推理是空間方向關系推理領域研究的重要內容，目前對空間方向關系推理的研究主要針對二維空間，三維空間方向關系推理研究相對滯后。

近年來，三維空間方向關系備受關注，一些模型相繼被提出，其中3DR27模型因其可計算性強，易于進行形式化推理，基于該模型的一些推理工作陸續展開。基于3DR27模型給出了單項與多項方向關系四種組合的復合推理方法，提高了模型的推理能力，但并未實現自動推理與計算，仍需要借助復雜的推理運算表。Wang等人［53］借助Balbiani的n維代數提出了一種3DR27模型下三維基本方向關系的復合推理方法，該方法需要借助該模型下三維矩形主方向關系的原關系計算，但目前尚沒有有效計算3DR27模型下三維矩形主方向原關系計算算法。3DR27模型下三維矩形主方向原關系的自動求解將是未來迫切需要解決的問題。

劉永山等人［54］基于三維空間單純型數據模型，采用投影的方法提出了一種三維空間物體方向關系的坐標映射模型，如圖14所示。該模型采用區間組合的形式表示三維空間方向關系，同時對三維空間中物體間方向關系的復合推理、反關系推理進行了研究，并給出了相應的推理規則。顧衛杰等人［55］提出了結合方向關系和拓撲關系的三維雙投影矩陣模型，該模型通過空間對象在xoy、xoz平面上的兩個投影矩陣聯合表達空間方向關系，給出了單項方向關系與多項方向關系四種組合推理方法，擯棄了繁瑣的組合推理運算表，但在表示物體間關系時不能有效區分空間對象是否相交的情形。

目前，關于空間方向關系復合推理的研究主要集中在三維精確對象，三維空間相對二維空間更為復雜，基本方位關系的數目繁多、推理工作任務繁重，依靠手工推理是不可行的，雖然已有一些推理方法相繼被提出，但這些工作大多依賴于推理運算法則和推理運算表，推理過程復雜繁瑣、計算量大。現有的三維方向關系模型的自動推理能力仍很欠缺，模型的自動推理能力亟待提高，這在一定程度上限制了現有方向關系模型推向實際應用，迫切需要發展三維空間方向關系自動推理算法，增強模型的實用性。

2.1.3 不確定方向關系復合推理

地理信息系統所描述的空間關系與人們所感知的真實對象間空間關系存在差異，即空間對象的不確定性。確定性對象方向關系表達與推理模型無法描述具有不確定性邊界的空間對象，因此必須要研究與之相適應的表達與推理模型，目前有關不確定對象方向關系推理的研究相對較少，是未來研究的熱點和難點。

董軼群等人［56］提出了一種基于MBR的不確定區域間方向關系建模方法，利用寬邊界表示區域的不確定邊界將矩形代數的良好性質應用于不確定區域間方向關系的表達與推理中，給出了相容性復合的定義，實現了不確定區域間方向關系的復合推理，為研究不確定區域間多種空間關系的組合表達與推理奠定基礎。陳娟等人［57］基于錐形主方向關系的寬邊界方向關系模型討論了寬邊界方向關系的反關系推理和復合推理，寬邊界方向關系取反和復合運算的約束網絡如圖15所示，但當出現內外區域結合或者更為復雜的情況無法進行推理。

Vague集作為模糊理論的重要分支，因其利用真假隸屬函數確定的子區間描述未確定的隸屬信息，極大增強了對模糊信息的處理能力，但目前同時考慮時間和空間因素的研究甚少，郝忠孝等人［58］提出了線性和周期性雙向疊合Vague時間段關系模型，給出了Vague時間段關系和Vague區域關系的復合推理規則和推理算法，為進一步研究Vague時間段關系、Vague區域關系及其復合推理奠定了基礎。以往的研究并未涉及Vague區域的Vague方向關系及復合推理問題，李松等人［59］基于Vague集，引入了同一推理簇的概念，給出了Vague區域關系和Vague方向關系的復合推理方法。

針對空間方向關系矩陣無法對凹多邊形對象進行有效的處理，康順等人［60］提出了凹邊形地標參照的外部性主方向關系與內部性主方向關系推理方法，以方向關系的邏輯和、邏輯差等代數運算推理兩個地標、一個地標參照下目標對象與參照對象之間的主方向關系。

不確定區域間方向關系的研究大多集中在空間關系的描述方面，推理方面研究相對較少，基于相容性復合的推理研究更是少之又少。粗糙集、模糊集和Vague集是目前應用比較廣泛的不確定性處理工具，利用隸屬度來表示不確定程度，在描述上與現實生活中人們的認知更加接近，但隸屬度函數比較難確定，計算量大，尋找統一的表達與推理模型有效地描述模糊空間對象是未來研究的重點。

2.2 空間方向關系的反關系推理

空間方向關系的反關系推理在現實中有著廣泛的應用，反關系推理即已知空間對象a相對b的方向關系推理空間對象b相對a可能的方向關系，它在節約空間方向關系存儲空間和提高方向關系推理效率及一致性檢驗等方面發揮著非常重要的作用。例如兩架戰機，假設已知它們的方位關系，那么可以利用反關系推理結果進行有針對性的避讓或打擊。

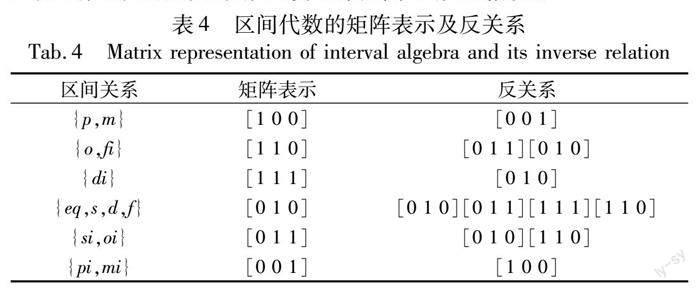
矩形代數與MBR模型下36種基本主方向關系存在等價聯系，借助MBR模型下基本主方向關系與矩形代數之間的等價聯系，可將該模型下基本主方向關系的反關系推理問題轉換為等價的矩形代數關系的反關系推理。利用表3所示的區間代數關系的矩陣表示及取反運算規則，應用矩陣運算實現MBR模型下二維基本主方向關系反關系的自動推理和計算。

上述反關系推理方法將空間對象抽象為點或利用對象的最小外包矩形代替空間對象本身，降低了表達與推理精度。為此，王淼等人［61］提出了一種基于區域對象本身的二維基本主方向關系的反關系推理算法，給出了方向關系矩陣模型下基本主方向關系的反關系推理算法，提高了推理精度。

為了避免繁瑣的手工推理，Wang等人［62］對方向關系矩陣模型下二維基本主方向關系的反關系推理進行研究，利用矩陣運算給出了該模型下二維基本主方向關系的反關系推理算法，提高了該模型的自動推理能力，增強了模型的實用性。目前，空間方向關系的反關系推理研究大多針對二維空間，三維空間方向關系反關系推理的研究相對滯后。Wang等［63］利用三維代數理論對3DR27模型下216中基本矩形主方向關系的反關系推理進行研究，借助三維代數與三維矩形主方向關系的等價聯系，將三維矩形主方向關系的反關系求解轉換為對等價的三維代數關系進行取反運算；在此基礎上，王淼等人［64］提出了3DR27模型基本矩形主方向關系原關系的概念，借助三維矩形主方向的原關系提出了該模型下三維基本主方向關系的反關系推理方法，但該方法仍依賴于三維矩形主方向關系原關系的手工推理和推理運算表。

目前，點對象方向關系的反關系推理、基于MBR模型和方向關系矩陣模型的基本主方向關系的反關系研究相對成熟。現有的主方向關系反關系方法利用點或矩形近似替代空間對象，這是不切實際的，雖提高了運算效率，但在一定程度上降低了表達與推理的精度。現實世界是一個三維空間，三維空間方向關系推理的研究相對滯后，特別是三維模糊空間對象方向關系反關系推理能力十分欠缺，雖有一些三維空間方向關系表達模型相繼提出，但由于三維空間固有的復雜性導致推理過程繁瑣，迫切需要完善和提高三維空間方向關系反關系的自動推理能力。

2.3 一致性檢驗

一致性檢驗（consistence checking）問題即給定一系列空間物體以及它們之間的方向關系，判斷這一系列方向關系所形成的空間網絡是否一致，即能否找到一組或一組以上的解滿足這些空間方向關系所形成的網絡。例如在空間數據庫中，它用于識別不一致的空間查詢請求并剔除相應的搜尋。

基于有向圖模型，利用自相矛盾的方式對區域對象的主方向關系網絡實施一致性檢驗，但該一致性檢驗方法計算復雜度較高；基于方向關系矩陣模型，當空間中兩個目標互為參照對象時的一致性檢驗算法可用于空間數據的查詢和數據質量的評價。

基于區間代數及矩形代數理論，結合MBR主方向關系模型將一維凸關系網格擴展到二維空間，如圖16所示，可實現MBR主方向關系運算及二元約束網絡一致性檢驗。

類飽和凸矩形關系是主方向關系的一個子類，針對非連通區域的矩形主方向關系的可達類飽和凸矩形關系的一致性檢驗算法的時間復雜度為O（n2），針對簡單區域的基本主方向關系約束一致性檢驗算法可在O（n4）結束。

目前關于空間方向關系網絡一致性檢驗的研究主要集中在二維主方向關系網絡。劉永山等人［54］基于3DR27模型對矩形主方向關系網絡一致性判定問題進行研究，將二維空間凸關系網絡擴展到三維，如圖17所示，在此基礎上給出了三維矩形主方向關系網絡一致性檢驗算法，為實現在三維空間方向關系網絡中尋找一致性場景奠定了基礎。

綜上所述，目前空間方向關系網絡一致性檢驗主要集中在二維區域對象方向關系網絡，三維空間方向關系網絡的一致性檢驗研究尚少。由于傳統的數學方法沒有根本性的突破，導致對主方向關系網絡一致性檢驗效率低下，對不確定對象主方向關系一致性檢驗幾乎是空白。空間方向關系一致性檢驗大多基于Ligozat的路徑一致性理論，通過選定某種方向關系模型，然后確定基于該模型的凸關系判定方法，進而給出具體的復合推理方法，如利用區間代數、方向關系矩陣等，最后套用“路徑一致的凸關系網絡是一致的”定理實現其一致性檢驗。現有的研究主要圍繞凸關系網絡展開，雖然采用復合推理方法不同，但最終的判定原理大都是依據路徑一致性理論，這類方法普遍計算復雜，時間效率低。如何突破傳統的路徑一致性理論，尋求更為高效的解決方法是需要深入研究的問題。

3 結合多方面空間信息的組合推理

定性空間推理主要針對方向關系、拓撲關系和距離關系，這三者有著緊密的聯系，從本質上看是相互支撐的。目前面向拓撲、方向、距離、尺度［65］等單一方面空間關系的表示與推理的研究相對成熟，然而采用單一空間關系難以對復雜的空間信息進行有效處理，結合多種空間信息的組合表達與推理成為近年來的研究熱點。

RCC-8是一個對邊界敏感的成熟模型，廣泛應用于定性空間推理領域，RCC-8定義了八種拓撲關系如圖18所示。基于RCC-8模型進行擴展用于處理拓撲和方位信息，明確指出其約束網相容性可由相應的RCC-8和矩形關系約束網的相容性判定，并證明了RCC-8模型與矩形代數的結合推理是易處理的，RCC-8模型與主方向關系演算的結合推理是一個NP完全問題。結合拓撲、尺寸和時間關系的統一表達模型具有簡潔、易于推理的特點，能夠有效地集成處理多方面時空信息。結合拓撲、方位和距離三種空間關系提出的擴展矩形模型，并給出了該模型下RCC-8、主方向關系和距離關系的轉換算法。但由于采用MBR表示空間對象，表達與推理的精度不高，結合RCC-8關系、矩形主方向關系以及定性尺寸關系三者結合的定性空間推理研究受到了廣泛關注，成為當前研究的熱點問題。

目前有關多種信息結合的空間方向關系推理主要集中在二維空間，賀玲玲[66］針對不同形狀的空間對象，提出了四類不同的三維空間方向關系模型，研究了三維空間方向關系與拓撲關系組合推理，使用邏輯推理和投影的方法推理三維空間拓撲關系，依據目標對象的不同，分別給出了相應的推理方法，但未考慮模糊空間對象方向關系。

模糊對象之間的拓撲關系至關重要，Guo等人［67］提出了一種區域間模糊空間對象拓撲關系定性分析方法，利用Jaccard相似度量計算區域間模糊拓撲關系矩陣與對應的精確拓撲關系矩陣之間的相似度，該方法符合人類的認知習慣，亦可滿足地理信息系統中各種實際應用需求。

雖然有向線與其他類型的空間物體（如區域和物體）之間的拓撲關系已經被廣泛研究，但很少有研究集中在有向線與有向區域之間的拓撲關系上。Shen等人［68］針對有向線—有向區域（DLDR）拓撲關系的表示和應用進行研究，用于計算和查詢精確的拓撲關系，有助于有向空間對象或時變對象的空間查詢和空間分析，同時提高了計算效率與推理精度。

目前方向關系推理研究大多針對靜態空間對象，當定性距離發生改變時難以對此作出有效推斷，針對方向關系與定性距離變化的組合推理問題，董軼群等人［69］提出了一種基于OPRA4方向關系推理定性距離變化的方法，用圓和射線之間的位置關系組合來描述相對移動方向，增強了對時空信息表達能力，提高了表達與推理精度。

目前有關空間場景相似性度量的研究，大多存在實體數目相對較少或者僅考慮空間關系中的單一關系、兩種組合關系的問題，王云閣等人［70］針對包含3個或3個以上相同實體數目的空間場景相似性度量問題提出了一種基于改進TDD模型的空間場景相似性度量方法，但該方法只考慮了空間關系相似性，沒有考慮空間目標的形狀特征，精度不高。

綜上所述，結合多種空間信息的方式主要有兩類：a）取關于每個空間方面的空間關系進行笛卡爾積形成新的關系處理；b）單獨處理每個空間方面，發掘新的推理算法來處理不同約束的結合以及它們之間的依賴性。結合方向關系和距離關系的復合模型比較適合大尺度空間，受空間對象形狀影響較小，能夠更準確地描述空間對象間的方位信息；結合方向關系和拓撲關系的復合模型適合描述小尺度空間下確定性對象之間的方位關系。雖然結合多種空間信息的復合模型相繼被提出，但結合仍不夠徹底，且對不確定性空間對象方向關系組合推理研究不夠，是未來研究的熱點和難點。

4 存在的問題及研究展望

空間方向關系形式化描述作為空間方向關系認知和推理的前提受到了國內外研究人員的廣泛關注，從點到區域、二維到三維、精確到模糊諸多表達模型相繼被提出。目前二維空間方向關系模型的研究已相對成熟，點對象間的模型主要有基于錐形的模型、基于投影的模型；確定區域間的模型主要有MBR模型、方向關系矩陣模型、Voronoi圖模型等；基于這些模型的改進模型。基于錐形的模型把參照對象當做一個點來處理，而當線和面作為參照對象時，錐形模型沒有把它們在大小和形狀上的差異描述出來，因而具有一定的局限性；方向關系矩陣模型較好地考慮到了空間對象自身的形狀和大小，但是忽略了距離帶來的影響；Voronoi圖模型彌補了上述不足，克服了空間對象的形狀、大小、距離等因素帶來的影響。綜上，當前二維空間方向關系表達與推理模型已日趨完善，但描述精度仍有待進一步提高，方向關系、距離關系、拓撲關系等多種空間關系的復合表達與推理是未來研究的重點，增強對空間對象的約束，獲得更為精準的空間信息。

目前，對不確定方向關系的模型研究仍很有限， 模型主要分為兩類：a）對精確對象方向關系模型進行擴展，使它能夠處分析不確定性對象方向關系；b）基于模糊集和粗糙集等不確定性集合理論的模型。基于精確對象方向關系模型的擴展模型描述簡單、易于理解，延伸了精確對象模型的適用范圍，但無法統一表示各種來源的模糊對象；粗糙集、模糊集和Vague集是目前應用比較廣泛的理論方法，利用隸屬度來表示不確定程度，在描述上與現實生活中人們的認知更加接近，但隸屬度函數比較難確定，計算量大，尋找統一的表示與推理模型有效處理不確定空間對象方位關系是未來研究的重點。

對確定性連通區域對象方向關系復合推理研究相對成熟，但由于一些模型計算復雜、可推理性差，大多依賴于復雜的推理運算法則和運算表，自動推理能力亟待提高，很難深入應用。三維空間基本方位關系數目繁多、推理過程復雜、工作量巨大，若依靠手工推理根本無法滿足實際應用需求，必須要大力發展三維空間方向關系的自動推理技術。此外，對于模糊方向關系的推理能力還很欠缺，特別是對三維模糊空間方向關系推理，由于三維空間固有的復雜性及對模糊數據處理本身具有一定的難度，使得三維模糊對象方向關系的復合，反關系推理和主方向關系一致性檢驗等問題十分困難，幾乎是當前研究的空白。基于點對象的空間方向關系推理已形成較為完備的理論體系，但由于將空間對象抽象為點，降低了表達與推理精度。基于區域對象的空間方向關系推理能力仍待提高，特別是三維不確定空間對象方向關系的推理能力仍很欠缺。

方向關系與距離和拓撲關系結合的研究相對較少，多種空間關系的結合還不夠徹底，有待進一步深入。目前大部分定性空間推理研究工作主要集中在對單一空間關系的理解和分析。實際應用中，單憑一種空間關系難以獲得對空間對象和空間關系客觀、全面的認知，需要融合多種空間信息以獲得對空間對象、關系更加細致、精確和完整的描述、理解和分析。因此，尋求有效結合不同空間演算的方法，充分利用多種空間信息提高空間方位關系表達與推理的精度，是空間關系推理領域需要突破的難點問題。

近年來，雖然有不少空間方向關系模型被提出，但由于一些模型的自身缺陷以及對相應的推理技術研究薄弱，導致空間方向關系的推理能力有限，這在一定程度上降低了模型的實用性。總體上說當前空間方向關系推理研究存在以下問題，同時也是后續研究中需要特別重視的問題及未來研究努力和發展的方向：

a）近年來，諸多空間方向關系模型相繼被提出，但一些模型計算復雜，可推理性差。未來研究應進一步增強模型的可計算性以及表達與推理能力，以提高模型的實用性，加強模型在GIS應用領域的研究。

b）關于空間方向關系推理工作主要集中在連通的、封閉的區域對象，然而現實生活中空間對象還以非連通區域形式存在，目前針對非連通區域復雜空間對象方向關系的表達與推理研究甚少，是未來研究的熱點和難點。

c）隨著對空間數據對象日益復雜的應用需求，三維空間方向的表達與推理日益成為研究的熱點，雖然已有一些三維空間方向關系的推理工作，但大多仍依賴于復雜、繁瑣的手工推理或推理運算表。總體上看，推理能力還很欠缺，三維空間基本方位關系數目繁多，若依靠手工推理，根本無法滿足實際應用需求，未來研究需要進一步加強對三維方向關系自動推理算法的研究。

d）目前空間方向關系網絡一致性檢驗方法雖采用的復合運算方法不盡相同，但最終的判定原理大都是基于路徑一致性理論，這些方法普遍復雜且計算量大，處理效率低下，根本無法滿足實際應用需求，未來應致力研究主方向關系網絡預處理和化簡方法，尋求主方向關系網絡自動化簡算法，尋求高效的空間方向關系網絡一致性判定算法。

e）區間代數理論在復合和取反等推理運算中具有一定的優越性，如何充分利用區間代數在定性空間推理中的優勢，提高現有模型的自動推理能力，擺脫復雜、復雜繁瑣的手工推理，實現二維和三維主方向關系的自動推理與計算，是未來需要深入研究和探索的問題。

f）未來應尋求統一描述精確對象和各種來源的模糊對象的表達與推理模型；對結合多方面信息的不確定空間關系的復合表達與推理進行研究，以提高對不確定空間關系的分析與處理能力。

g）易于進行形式化推理的模糊對象方向關系模型并不多見，特別是對于三維空間模糊對象，由于三維空間固有的復雜性及對不確定性數據的描述本身具有一定的難度，那么對于三維模糊對象空間方向關系的描述就更加復雜和困難。當前對三維模糊對象方向關系的研究十分欠缺，在國內外相關研究尚不多見，未來需進一步完善和提高對三維模糊空間方向關系的建模及推理能力。

h）目前，對空間方位關系的研究主要集中在對空間方位關系的建模及推理技術研究，對空間方位關系查詢的應用研究不夠。隨著基于位置服務應用的不斷深入，建議未來應加強結合空間方位信息的位置服務應用的研究，例如基于空間方位信息的興趣點推薦等。

i）空間方位關系在空間數據分析應用領域的研究將是未來研究的熱點問題，應進一步加強空間方位信息在空間數據挖掘，空間分析與空間決策等相關實際應用領域的研究。

5 結束語

隨著空間應用方位關系應用的不斷深入，對方向關系表達與推理的精度提出了新的、更高的要求，尋求接近真實物體的空間方位關系精細化表達與推理是未來迫切需要解決的問題。此外，由于一些模型自身的局限性以及對相應的推理技術研究薄弱，導致空間方向關系的推理能力仍很有限，尤其是三維空間基本方位關系數目繁多，推理過程復雜、繁瑣，若依靠手工推理，根本無法滿足實際應用需求。因此，研究與發展空間方向關系的自動推理技術，是未來開展研究的重要方向。本文對各類空間方向關系模型的特性及適用范圍進行比較和分析，并對空間方向關系復合推理、反關系推理、空間網絡一致性判定和結合多方面信息的空間方位關系推理等研究現狀進行總結分析，最后指出空間方向關系表達與推理研究存在的不足及未來研究方向。

參考文獻：

[1]王彥坤，樊紅，王偉璽，等.地標空間方向的位置描述定位模型[J］.測繪科學，2020，45（9）：18-24.（Wang Yankun，Fan Hong，Wang Weixi，et al.A positioning localities model about landmark locality description based on spatial direction relationship[J］.Science of Surveying and Mapping，2020，45（9）：18-24.）

［2]Liang Hui，Lyu Kailu，Sun Yusheng，et al.Semantic-driven 3D scene construction based on spatial relationship and case-base[C］// Proc of the 7th IEEE International Conference on Virtual Reality.Piscataway，NJ：IEEE Press，2021：54-61.

［3]王淼，王曉桐，李松，等.二維基本矩形主方向關系的原關系推理[J］.西安交通大學學報，2020，54（4）：133-143.（Wang Miao，Wang Xiaotong，Li Song，et al.Reasoing with the original relations of the basic 2D rectangular cardinal direction relation[J］.Journal of Xian Jiaotong University，2020，54（4）：133-143.）

［4]張韻，彭建東，王晶晶，等.基于地學信息圖譜的江漢平原土地利用時空變化分析[J］.水土保持研究，2020，27（4）：85-92.（Zhang Yun，Peng Jiandong，Wang Jingjing，et al.Analysis on spatial and temporal change of land use in Jianghan plain based on geo-information atlas[J］.Research of Soil and Water Conservation，2020，27（4）：85-92.）

［5]郝忠孝.時空數據庫查詢與推理［M］.北京：科學出版社，2010.（Hao Zhongxiao.Query and Inference of spatio-temporal database[M］.Beijing：China Science Publishing & Media Ltd.，2010.）

［6]白梅，萇仕涵，王習特.基于位置的路網Skyline查詢處理研究［J］.計算機工程，2022，48（1）：127-134.（Bai Mei，Chang Shihan，Wang Xite.Research on location-based skyline queries processing in road network［J］.Computer Engineering，2022，48（1）：127-134.）

［7]郭亮亮，靳燕，楊博，等.一種基于兩級緩存的高效時序數據庫系統[J］.測試技術學報，2022，36（2）：147-152.（Guo Liangliang，Jin Yan，Yang Bo，et al.A high-efficiency time series database system based on two-level cache[J］.Journal of Test and Measurement Technology，2022，36（2）：147-152.）

［8]王淼，李松陽.空間方向關系形式化描述研究進展[J］.計算機應用，2013，33（5）：1324-1329.（Wang Miao，Li Songyang.Research survey on formal description for direction relations[J］.Journal of Computer Applications，2013，33（5）：1324-1329.）

［9]安曉亞，劉平芝，金澄，等.手繪地圖開域空間方向關系檢索法[J］.測繪學報，2017，46（11）：1899-1909.（An Xiaoya，Liu Pingzhi，Jin Cheng，et al.A hand-drawn map retrieval method based on open area spatial direction relation[J］.Acta Geodaetica et Cartographica Sinica，2017，46（11）：1899-1909.）

［10]閆浩文.空間相似關系的理論體系與潛在研究方向[J/OL］.測繪學報，http：//kns.cnki.net/kcms/detail/11.2089.p.20230328.0830.002.htm.（Yan Haowen.Theoretical system and potential research issues of spatial similarity relations[J/OL］.Acta Geodaetica et Cartographica Sinica，http：//kns.cnki.net/kcms/detail/11.2089.p.20230328.0830.002.htm.）

［11]Xu Yongyang，Chen Zhanlong，Xie Zhong，et al.Quality assessment of building footprint data using a deep autoencoder network[J］.International Journal of Geographical Information Science，2017，31（10）：1929-1951.

［12]石雪.基于層次化混合模型的高分辨率遙感影像分割方法研究[J］.測繪學報，2023，52（1）：168.（Shi Xue.Hierarchical mixture model based high-resolution remote sensing image segmentation method[J］.Acta Geodaetica et Cartographica Sinica，2023，52（1）：168.）

［13]何云斌，董恒，萬靜，等.基于密度峰值和近鄰優化的聚類算法［J］.計算機科學與探索，2020，14（4）：554-565.（He Yunbing，Dong Heng，Wan Jing，et al.Clustering algorithm based on density peak and neighbor optimization［J］.Journal of Frontiers of Computer Science & Technology，2020，14（4）：554-565.）

［14]李松，竇雅男，郝曉紅，等.道路網環境下K-支配空間Skyline查詢方法[J］.計算機研究與發展，2020，57（1）：227-239.（Li Song，Dou Yanan，Hao Xiaohong，et al.Method of the K-Dominant space Skyline query in road network［J］.Journal of Computer Research and Development，2020，57（1）：227-239.）

［15]Li Song，Song Shuang，Hao Xiaohong，et al.Directional nearest neighbor query method for specified geographical direction space based on Voronoi diagram[J］.High Technology Letters，2022，28（2）：122-133.

［16]李朋朋，劉紀平，閆浩文，等.基于方向關系矩陣的空間方向相似性計算改進模型[J］.測繪科學技術學報，2018，35（2）：215-220.（Li Pengpeng，Liu Jiping，Yan Haowen，et al.An improved model for calculating the similarity of spatial direction based on direction relation matrix[J］.Journal of Geomatics Science and Technology，2018，35（2）：215-220.）

［17]龔希，謝忠，周林，等.空間方向相似性二元組模型度量方法[J］.測繪學報，2021，50（12）：1705-1716.（Gong Xi，Xie Zhong，Zhou Lin，et al.A two-tuple model based spatial direction similarity measurement method[J］.Acta Geodaetica et Cartographica Sinica，2021，50（12）：1705-1716.）

［18]宗琴，劉艷霞，張慧麗.一種基于復合表達模型的方向相似性算法[J］.測繪科學技術學報，2020，37（1）：90-95.（Zong Qin，Liu Yanxia，Zhang Huili.A directional similarity algorithm based on composite representation model[J］.Journal of Geomatics Science and Technology，2020，37（1）：90-95.）

［19]陳超，王中輝，馬品.面狀群 （組） 目標空間方向關系的形式化描述與計算[J］.測繪與空間地理信息，2021，44（9）：17-21.（Chen Chao，Wang Zhonghui，Ma Pin.Formal description and computation of the spatial direction relationships between polygonal object groups[J］.Geomatics and Spatial Information Technology，2021，44（9）：17-21.）

［20]祿小敏，閆浩文，王中輝.群組目標空間方向關系研究進展[J］.地理信息世界，2018，25（1）：28-31.（Lu Xiaomin，Yan Haowen，Wang Zhonghui.Research progress of spatial direction relations between object groups[J］.Geomatics World，2018，25（1）：28-31.）

［21]祿小敏，閆浩文，王中輝.群組目標空間方向關系建模[J］.地球信息科學學報，2018，20（6）：721-729.（Lu Xiaomin，Yan Haowen，Wang Zhonghui.The modeling of spatial direction relationship between object groups[J］.Journal of Geo-information Science，2018，20（6）：721-729.）

［22]楊強.基于Delaunay三角剖分的二維交互建模研究[J］.物探化探計算技術，2021，43（2）：256-260.（Yang Qiang.Study of two-dimensional interactive modeling based on Delaunay triangulation[J］ Computing Techniques for Geophysical and Geochemical Exploration，2021，43（2）：256-260.）

［23]李艷波.自適應鄰域形態學理論及其FPGA實現[D］.西安：西安電子科技大學，2019.（Li Yanbo.Adaptive neighborhood morphology theory and Its FPGA implementation[D］.Xian：Xidian University，2019.）

［24]王玉竹，閆浩文.一種改進的群組目標空間方向關系計算模型[J］.測繪科學，2022，47（4）：169-174.（Wang Yuzhu，Yan Haowen.An improved computational model on spatial direction between object groups[J］.Science of Surveying and Mapping，2022，47（4）：169-174.）

［25]江坤，王中輝.錐形模型的面群方向關系相似性度量方法[J］.測繪科學，2022，47（6）：174-180.（Jiang Kun，Wang Zhonghui.A similarity measurement method for direction relationship of surface groups based on cone model[J］.Science of Surveying and Mapping，2022，47（6）：174-180.）

［26]Wang Kaihong，Guan Xuelun.3D reconstruction and rendering models in urban architectural design using Kalman filter correction algorithm[J］.Wireless Communications and Mobile Computing，2022，2022（1）：articleID 8530795.

［27]Lundgren A V A.Systematic review of computer vision semantic analysis in socially assistive robotics[J］.AI，2022，3（1）：229-249.

［28]Yin Fan，Li Chao，Wang Haibin，et al.Automatic tracking of weak acoustic targets within Jamming Environment by using image processing methods[J］.Applied Sciences，2022，12（13）：6698-6698.

［29]劉慶，楊宇航，陳侃侃.測繪地理信息系統的架構與功能[J］.電子測試，2022，36（6）：72-76.（Liu Qin，Yang Yuhang，Chen Kaikai.Architecture and function of surveying and mapping geographic Information system[J］.Electronic Test，2022，36（6）：72-76.）

［30]王淼，郝忠孝.三維空間方向關系的定性描述與推理[J］.計算機工程，2009，35（15）：22-25.（Wang Miao，Hao Zhongxiao.Qualitative representation and reasoning on direction relation of Three-dimension space[J］.Computer Engineering，2009，35（15）：22-25.）

［31]齊新軍，宗明魁.3DR34關系模型表示與分析[J］.煤炭技術，2011，30（3）：210-212.（Qi Xinjun，Zong Mingkui.Representation and analysis of 3DR34 relation model[J］.Coal Technology，2011，30（3）：210-212.）

［32]趙碩，張麗平.3DR39模型及雙向關聯表示[J］.科技通報，2011，27（3）：412-415，420.（Zhao Shuo，Zhang Liping.3DR39 model and the bidirectional association representation[J］.Bulletin of Science and Technology，2011，27（3）：412-415，420.）

［33]郝曉紅，張麗平，李松.三維空間中3DR44方向關系表示模型[J］.計算機工程，2011，37（1）：75-77，80.（Hao Xiaohong，Zhang Liping，Li Song.3DR44 direction relation representation model in three dimensional space[J］.Computer Engineering，2011，37（1）：75-77，80.）

［34]郝曉紅，李松，郝忠孝.復雜3D空間中的3DR46模型的表示與推理[J］.計算機科學與探索，2020，14（12）：2004-2013.（Hao Xiaohong，Li Song，Hao Zhongxiao.Representation and reasoning for model of 3DR46 in complex 3D space[J］.Journal of Frontiers of Computer Science & Technology，2020，14（12）：2004-2013.）

［35]趙澤茹.基于3DR50方向關系模型查詢算法[D］.秦皇島：燕山大學，2017.（Zhao Zeru.Query algorithm of direction relation model based on 3DR50[D］.Qinhuangdao：Yanshan University，2017.）

［36]郝曉紅，張麗平，趙齡強，等.3DR39-3d方位關系模型與反方位關系[J］.計算機工程，2014，40（7）：258-262.（Hao Xiaohong，Zhang Liping，Zhao Lingqiang，et al.3DR39-3d orientation relationship model and reverse orientation relation[J］.Computer Engineering，2014，40（7）：258-262.）

［37]郝曉紅，李松，張麗平.3DR44-4d方位關系表示模型[J］.計算機工程，2012，38（3）：57-59.（Hao Xiaohong，Li Song，Zhang Liping.Representation model of 3DR44-4d orientation relation[J］.Computer Engineering，2012，38（3）：57-59.）

［38]賈曉晴.基于3D-ICSRM模型的空間關系推理方法研究[D］.秦皇島：燕山大學，2017.（Jia Xiaoqing.Research on spatial relation reasoning method based on 3D-ICSRM model[D］.Qinhuangdao：Yanshan University，2017.）

［39]歐陽繼紅，祝東紅，富倩，等.基于OPRAm的三維相對方位關系模型[J］.吉林大學學報：工學版，2015，45（5）：1535-1540.（Ouyang Jihong，Zhu Donghong，Fu Qian，et al.Model for three-directional relative directions based on OPRAm[J］.Journal of Jilin University：Engineering and Technology Edition，2015，45（5）：1535-1540.）

［40]Zhou Shuang，Zhang Jianguo，Zhang Qingyuan，et al.Uncertainty theory-based structural reliability analysis and design optimization under epistemic uncertainty[J］.Applied Sciences，2022，12（6）：2846.

［41]Chen Hao，Vasardani M，Winter S，et al.A graph database model for knowledge extracted from place descriptions[J］.International Journal of Geo-Information，2018，7（6）：221-250.

［42]Xiang Jun.A novel direction relation reasoning model based environmental protection GIS[C］// Proc of IOP Conference Series：Earth and Environmental Science.［S.l.］：IOP Publishing Ltd.，2021：012047.

［43]李松，郝忠孝.基于Vague集的含洞不規則Vague區域關系[J］.計算機研究與發展，2009，46（5）：823-831.（Li Song，Hao Zhongxiao.Region relations of the irregular Vague regions with holes based on Vague sets[J］.Journal of Computer Research and Development，2009，46（5）：823-831.）

［44]郝忠孝，李松.基于Vague集的動態Vague區域關系[J］.軟件學報，2009，20（4）：878-889.（Hao Zhongxiao，Li Song.Dynamic Vague region relations based on Vague sets[J］.Journal of Software，2009，20（4）：878-889.）

［45]董軼群，徐文星，劉建東，等.不確定邊界區域間方向關系建模方法[J］.北京郵電大學學報，2016，39（1）：18-23.（Dong Yiqun，Xu Wenxing，Liu Jiandong，et al.Approach to modeling direction relations between regions with uncertain boundaries[J］.Journal of Beijing University of Posts & Telecommunications，2016，39（1）：18-23.）

［46]González-Rodríguez L，Plasencia-Salgueiro A.Uncertainty-aware autonomous mobile robot navigation with deep reinforcement learning[M］// Deep Learning for Unmanned Systems.Cham：Springer，2021：225-257.

［47]Midoun M，Belbachir H.A new process for mining spatial databases：combining spatial data mining and visual data mining[J］.International Journal of Business Information Systems，2022，39（1）：17-51.

［48]秦昆，許凱，吳濤，等.智能空間信息處理與時空大數據分析探索[J］.地理空間信息，2022，20（12）：1-11.（Qin Kun，Xu Kai，Wu Tao，et al.Intelligent spatial information processing and Spatio-temporal big data analysis exploration[J］.Geospatial Information，2022，20（12）：1-11.）

［49]萬靜，齊坡.基于矩陣模型的方向關系表示與推理[J］.計算機工程與設計，2014，35（10）：3589-3593，3650.（Wan Jing，Qi Po.Representation and reasoning of direction relations based on matrix model[J］.Computer Engineering and Design，2014，35（10）：3589-3593，3650.）

［50]歐陽繼紅，孫偉，劉大有，等.方向關系矩陣的復合[J］.吉林大學學報：工學版，2010，40（4）：1048-1053.（Ouyang Jihong，Sun Wei，Liu Dayou，et al.Composition of direction relation matrix[J］.Journal of Jilin University：Engineering and Technology Edition，2010，40（4）：1048-1053.）

［51]王淼，郝忠孝.采用定性坐標的位置表達及主方向關系推理[J］.西安交通大學學報，2010，44（8）：36-42.（Wang Miao，Hao Zhongxiao.Location representation and cardinal direction relation reasoning based on qualitative coordinates[J］.Journal of Xian Jiaotong University，2010，44（8）：36-42.）

［52]丹曉飛.一種面向點對象的空間方位關系的柵格表達[D］.武漢：湖北大學，2021.（Dan Xiaofei.A raster representation of spatial orientation relation for point objects[D］.Wuhan：Hubei University，2021.）

［53]Wang Miao，Liu Xiaodong，Li Songyang，et al.Composing 3D cardinal direction relations[J］.Journal of Computational and Theoretical Nanoscience，2016，13（1）：623-627.

［54]劉永山，成雪琴.基于坐標映射模型的方向關系一致性檢驗[J］.計算機工程，2011，37（16）：68-71.（Liu Yongshan，Cheng Xueqin.Consistency check for direction relations based on coordinate mapping model[J］.Computer Engineering，2011，37（16）：68-71.）

［55]顧衛杰，劉永山.雙投影矩陣模型的方向關系組合推理研究[J］.測繪科學技術學報，2014，31（5）：538-542，546.（Gu Weijie，Liu Yongshan.Research on directional relation combinational reasoning of double projections matrix model[J］.Journal of Geomatics Science and Technology，2014，31（5）：538-542，546.）

［56]董軼群，劉大有，王芳，等.一種基于MBR的不確定區域間方向關系建模方法[J］.電子學報，2011，39（2）：329-335.（Dong Yiqun，Liu Dayou，Wang Fang，et al.A MBR-based approach for modeling direction relations between uncertain regions[J］.Acta Electronica Sinica，2011，39（2）：329-335.）

［57]陳娟，劉大有，賈海洋.不確定區域間定性方向關系模型[J］.吉林大學學報：工學版，2013，43（1）：111-116.（Chen Juan，Liu Dayou，Jia Haiyang.Modelling qualitative direction relations between indeterminate regions[J］.Journal of Jilin University：Engineering and Technology Edition，2013，43（1）：111-116.）

［58]郝忠孝，李松.Vague時間段關系與Vague區域關系的表示和復合推理[J］.計算機學報，2014，37（8）：1743-1753.（Hao Zhongxiao，Li Song.Representation and compound reasoning of the vague temporal interval relations and the vague region relations[J］.Chinese Journal of Computers，2014，37（8）：1743-1753.）

［59]李松，張麗平，郝曉紅，等.Vague區域關系與方向關系的表示及復合推理[J］.計算機研究與發展，2015，52（4）：918-928.（Li Song，Zhang Liping，Hao Xiaohong，et al.Representation and compound reasoning of Vague region relations and direction relations[J］.Journal of Computer Research and Development，2015，52（4）：918-928.）

［60]康順，李佳田，瞿珊珊.凹邊形地標參照的主方向關系推理方法[J］.武漢大學學報：信息科學版，2018，43（1）：24-30.（Kang Shun，Li Jiatian，Qu Shanshan.A qualitative reasoning method for cardinal directional relations under concave landmark referencing[J］.Geomatics and Information Science of Wuhan University，2018，43（1）：24-30.）

［61]王淼，何莉，李松.基本主方向關系的反關系推理[J］.計算機應用研究，2013，30（1）：138-141.（Wang Miao，He Li，Li Song.Research on inversing basic cardinal direction relation[J］.Application Research of Computers，2013，30（1）：138-141.）

［62]Wang Miao，Fang Zhenxi，Liu Weiguang，et al.Computing the inverse of cardinal direction relations between regions[J］.Journal of Intelligent Systems，2022，31（1）：1160-1177

［63]Wang Miao，Li Song.Reasoning with the inverse of 3D rectangular cardinal direction relations[J］.ICIC Express Letters，Part B：Applications，2013，4（3）：581-587.

［64]王淼，黃治國，李松.基于代數理論的三維主方向關系的反關系推理[J］.計算機應用，2014，34（4）：1144-1148.（Wang Miao，Huang Zhiguo，Li Song.Inverse reasoning of 3D cardinal direction relations based on block algebra[J］.Journal of Computer Applications，2014，34（4）：1144-1148.）

［65]艾廷華，張翔.地理信息科學中尺度概念的詮釋與表達[J］.測繪學報，2022，51 （07）：1640-1652.（Ai Tinghua，Zhang Xiang.An interpretation and representation of scale concept in geo-information sciences[J］.Acta Geodaetica et Cartographica Sinica，2022，51 （07）：1640-1652.）

［66]賀玲玲.三維空間方向關系與拓撲關系推理方法研究[D］.秦皇島：燕山大學，2015.（He Lingling.Research on three-dimensional spatial direction Relation and topological Relation inference method[D］.QinHuangDao City：Yanshan University，2015.）

［67]Guo Jifa，Shao Xiaodong，Mo Xunqiang.Qualitative topological relations between interval type-2 fuzzy spatial objects[J］.Transactions in GIS：TG，2018，22 （6）：1596-1631.

［68]Shen Jingwei，Huang Yang，Chen Min.Topological relations between a directed line and a directed region[J］.Transactions in GIS：TG，2020，24 （2）：526-548

［69]董軼群，劉建東，徐文星，等.一種基于OPRA_4方向關系推理定性距離變化的方法[J］.計算機研究與發展，2020，57（5）：971-983.（Dong Yiqun，Liu Jiandong，Xu Wenxing，et al.A reasoning method for qualitative distance change based on OPRA_4 direction relations[J］.Computer Research and Development，2020，57（5）：971-983.）

［70]王云閣，郭黎，李豪，等.一種基于改進TDD模型的間場景相似性度量方法[J］.測繪科學技術學報，2021，38（3）：309-315.（Wang Yunge，Guo Li，Li Hao，et al.A method for measuring space scene similarity based on improved TDD model[J］.Journal of Geomatics Science and Technology，2021，38（3）：309-315.）

收稿日期：2023-02-09；

修回日期：2023-04-10

基金項目：國家自然科學基金資助項目（61802115，62173126）；河南省科技攻關項目（232102210068，232102210156，232102210085）；河南省高等學校重點科研項目（23A510018）

作者簡介：王淼（1981-），男，河南光山人，副教授，博士，CCF會員，主要研究方向為數據庫理論與應用、空間關系、空間數據查詢與推理等（wmscan@tom.com）；方振西（1996-），男，河南商丘人，碩士研究生，主要研究方向為數據庫理論與應用、空間推理、空間關系等；王曉桐（1994-），女，河南光山人，博士研究生，主要研究方向為生物信息學、空間數據庫理論與應用等；李松（1977-），男，江蘇徐州人，教授，博士，主要研究方向為數據庫理論與應用、數據挖掘、數據查詢和推理等；郝忠孝（1940-），男，山東煙臺人，教授，博導，主要研究方向為數據庫理論與應用、時空數據庫、主動數據庫、數據查詢和推理等．