基于改進(jìn)CBS算法的自動(dòng)化碼頭多AGV無沖突路徑規(guī)劃

周欣慈 朱瑾

摘 要：針對自動(dòng)化集裝箱碼頭上自動(dòng)引導(dǎo)車（automated guided vehicle，AGV）數(shù)量增加導(dǎo)致沖突更頻繁。提出一種改進(jìn)的基于沖突的搜索（conflict based search，CBS）算法。底層采用基于曼哈頓距離的 A*算法，上層結(jié)合二叉樹原理建立沖突樹對AGV之間的沖突進(jìn)行規(guī)避。以最小化AGV在岸橋和堆場之間的總路徑長度為目標(biāo)，使用柵格法建立AGV路網(wǎng)模型。考慮AGV之間的點(diǎn)沖突與邊沖突，將自動(dòng)化碼頭多AGV無沖突路徑規(guī)劃問題規(guī)約為多智能體尋徑問題。實(shí)驗(yàn)結(jié)果表明，所提出的算法在保證堵塞率為0%的前提下，縮短總路徑長度并提高運(yùn)算速度，驗(yàn)證算法的有效性。

關(guān)鍵詞：自動(dòng)化碼頭； 多AGV； 多智能體路徑規(guī)劃（MAPF）； 基于沖突的搜索算法（CBS）

中圖分類號(hào)：TP242?? 文獻(xiàn)標(biāo)志碼：A

文章編號(hào)：1001-3695（2023）09-010-0000-00

doi：10.19734/j.issn.1001-3695.2023.02.0036

Conflict-free path planning for multi-AGVs in automated terminals

based on improved CBS algorithm

Zhou Xinci， Zhu Jin

（Institute of Logistics Science & Engineering， Shanghai Maritime University， Shanghai 201306， China）

Abstract：Increased number of automated guided vehicles（AGV） on automated container terminals leads to more frequent conflicts. This paper proposed an improved conflict based search（CBS） algorithm. The bottom layer used the A* algorithm based on Manhattan distance， and the top layer combined the binary tree principle to build conflict trees to avoid conflicts between AGV. With the objective of minimizing the total path length of AGV between the shore bridge and the yard， the grid method used to developed the AGV road network mode. Considering the point conflict and edge conflict among AGV， the multi-AGV conflict-free path planning problem in automated terminals statuted as a multi-agent pathplanning problem. The experimental results show that the proposed algorithm shortens the total path length and increases the computational speed with a guaranteed blockage rate of 0%， which verifies the effectiveness of the algorithm.

Key words：automated terminals; multi-AGV; multi-intelligent path planning（MAPF）; conflict-based search algorithm（CBS）

0 引言

AGV是自動(dòng)化碼頭水平運(yùn)輸作業(yè)的重要設(shè)備，是集裝箱運(yùn)輸?shù)闹饕ぞ摺Ｔ谌斯げ僮鳌⒋笠?guī)模操作和智能碼頭難度不斷增加的影響下，AGV的數(shù)量不斷增加，同時(shí)數(shù)量增加也導(dǎo)致設(shè)備在運(yùn)行中出現(xiàn)等待、沖突、死鎖等問題。影響AGV運(yùn)輸?shù)男剩岣逜GV運(yùn)行速度成為自動(dòng)化碼頭現(xiàn)階段急需解決的問題。

針對自動(dòng)化碼頭多AGV路徑規(guī)劃問題，眾多學(xué)者進(jìn)行了研究。例如，丁一等人［1］建立兩階段模型，使用最短路徑算法規(guī)劃路徑；張其嬌等人［2］提出結(jié)合沖突規(guī)避的加權(quán)實(shí)時(shí)A*算法；牛雅倩等人［3］提出基于動(dòng)態(tài)平衡策略的控制方式，改進(jìn)Dijkstra算法規(guī)劃AGV路徑；郭昆侖等［4］以最小化AGV在岸橋和堆場的作業(yè)堵塞率為目標(biāo)，設(shè)計(jì)基于多智能體系統(tǒng)的體系結(jié)構(gòu)；蘭培真等人［5］提出基于ant-agent的AGV控制算法，將AGV視為螞蟻智能體，解決AGV道路死鎖與路徑?jīng)_突問題；曾慶成等人［6］考慮AGV的擁堵因素建立動(dòng)態(tài)模型，使用蟻群算法求解，有效提高運(yùn)輸作業(yè)的效率；Zhong等人［7］建立混合整數(shù)規(guī)劃模型，驗(yàn)證帶有模糊控制器的混合遺傳算法—粒子群優(yōu)化算法的有效性；Yue等人［8］提出一種兩階段混合整數(shù)優(yōu)化模型，使用改進(jìn)的基于規(guī)則的啟發(fā)式算法，Dijkstra算法和Q-learning算法集成，設(shè)計(jì)基于圖論的路徑?jīng)_突避免策略有效減少?zèng)_突。現(xiàn)有的文獻(xiàn)對于自動(dòng)化碼頭上多AGV路徑規(guī)劃的研究規(guī)模在30臺(tái)左右，而目前國內(nèi)主要自動(dòng)化碼頭AGV的數(shù)量是18，38，60，甚至136臺(tái)，解決大規(guī)模的AGV路徑規(guī)劃問題更具實(shí)際意義。

多智能體路徑規(guī)劃（multi-agent path find-ing，MAPF）問題是一類尋找多個(gè)智能體從起始位置到目標(biāo)位置且無沖突的最優(yōu)路徑集合的問題，在柔性制造系統(tǒng)中如物流中心，智能車間，智能倉儲(chǔ)的AGV上有實(shí)際應(yīng)用。考慮最優(yōu)解法器Goldenberg等人［9］提出增強(qiáng)部分?jǐn)U展改進(jìn)A*搜索（EPEA*）算法，只擴(kuò)展最優(yōu)節(jié)點(diǎn)，修改當(dāng)前節(jié)點(diǎn)的啟發(fā)函數(shù)值并重新加入open-list來求解中的MAPF問題，改進(jìn)了分支因子的缺陷；Sharon等人［10］提出基于代價(jià)增長樹搜索（increaing cost tree search，ICTS）算法求解中的MAPF問題，闡述ICTS算法在智能體密度較高和沖突代價(jià)較大的局限性；Surynek［11］將MAPF問題規(guī)約為SAT問題，將問題中地圖的結(jié)構(gòu)、智能體的位置和約束編碼為布爾變量，然后用這些布爾變量生成標(biāo)準(zhǔn)的 SAT 問題來驗(yàn)證是否存在全局代價(jià)為C的可行解，遍歷所有可能的全局代價(jià)C就能夠生成全局最優(yōu)解；Sharon等人［12］提出基于CBS算法解決MAPF問題，并與ICTS進(jìn)行對比實(shí)驗(yàn)，驗(yàn)證CBS在求解速度和求解質(zhì)量的有效性；Hnig等人［13］將MAPF應(yīng)用在倉儲(chǔ)上，縮短理論與現(xiàn)實(shí)的局限性；黃鼎勇等人［14］使用CBS算法求解多無人機(jī)路徑規(guī)劃，考慮轉(zhuǎn)彎成本，防止安全區(qū)域無人機(jī)的相互碰撞；郭超等人［15］采用基于時(shí)空A*算法求解物流中心的MAPF問題，引入沖突規(guī)避以避免與其他路徑發(fā)生沖突；劉恒麟［16］使用CBS算法應(yīng)用在智能倉儲(chǔ)的多AGV路徑規(guī)劃問題上，與傳統(tǒng)的A*算法進(jìn)行對比實(shí)驗(yàn)，驗(yàn)證CBS算法在減少運(yùn)算時(shí)間的有效性；由于自動(dòng)化碼頭AGV運(yùn)行環(huán)境更復(fù)雜，地圖規(guī)模更大，現(xiàn)有文獻(xiàn)使用MAPF模型及CBS算法應(yīng)用在自動(dòng)化碼頭上，求解大規(guī)模AGV無沖突路徑規(guī)劃較少。

本文提出基于沖突規(guī)避策略的自動(dòng)化大規(guī)模AGV無沖突路徑規(guī)劃算法，采用改進(jìn)的CBS算法求解該MF問題，針對小規(guī)模算例，設(shè)計(jì)基于ICTS和基于CBS算法的對比實(shí)驗(yàn)，比較算法在不同數(shù)量下AGV的平均運(yùn)算時(shí)間和平均總路徑長度；針對大規(guī)模算例，采用基于CBS算法求解自動(dòng)化碼頭上60臺(tái)AGV的多智能體路徑規(guī)劃問題并分析平均運(yùn)算時(shí)間和平均總路徑長度。

1 模型建立

1.1 模型假設(shè)

a）岸橋和堆場位置固定不變且已知，一個(gè)岸橋?qū)?yīng)所有堆場箱區(qū)；b）每臺(tái)AGV型號(hào)規(guī)格相同；c）AGV運(yùn)行速度恒定（包括在轉(zhuǎn)彎時(shí)）；d）不考慮AGV在行駛過程中故障、天氣、電量等因素的影響；e）在岸橋與堆場之間設(shè)置緩沖區(qū)，其中空閑AGV停車區(qū)設(shè)置為靜態(tài)障礙物，AGV在執(zhí)行水平運(yùn)輸作業(yè)時(shí)不可通行；f）AGV在岸橋與堆場裝卸集裝箱的時(shí)間忽略不計(jì)；g）所有AGV柵格路線可雙向行駛；h）每個(gè)時(shí)間點(diǎn)每個(gè)柵格只允許一臺(tái)AGV占用，岸橋處的柵格可以允許多AGV占用。

1.2 變量設(shè)定

在表示自動(dòng)化碼頭AGV水平運(yùn)輸區(qū)的路徑網(wǎng)時(shí)，用G=（V，E，ob）有向加權(quán)圖表示AGV的路網(wǎng)。其中V表示自動(dòng)化碼頭上AGV柵格圖的所有節(jié)點(diǎn)編號(hào)的集合，V=［（x1，y1），（x2，y2），…，（xn，yn）］，其中n×n 表示柵格的數(shù)量，而E為V的邊集，表示每個(gè)V對應(yīng)的長度，ob表示障礙物坐標(biāo)的集合。其他變ob=［（xm，y1），（xm，y2），…，（xm，yn）］量設(shè)置如表1所示。

1.3 數(shù)學(xué)模型

目標(biāo)函數(shù)：

min∑Ni=1Coni（1）

約束條件：

Xij=1 AGV訪問節(jié)點(diǎn)i后訪問節(jié)點(diǎn)j0 否則（2）

∑Ni=1∑Nj=1Xij=1（3）

T=Cov（4）

f（i）=g（i）+h（i）（5）

h（i）=|Pi[t][0]-gi[0]|+|Pi[t][1]-gi[1]|（6）

Td=∑ki=1tdi（7）

mov=1 表示AGV在原地等待0 否則（8）

Co=∑ki=1Pi-1（8）

其中：式（1）表示本模型的目標(biāo)函數(shù)是總代價(jià)最小，式（2）（3）表示同一時(shí)間每個(gè)節(jié)點(diǎn)至多被AGV訪問一次，式（4）表示所有AGV完成任務(wù)的時(shí)間，式（5）表示底層使用的A*算法，其中f（i）是估算函數(shù)，g（i）是從起始節(jié)點(diǎn)到節(jié)點(diǎn)i的實(shí)際成本，h（i）是節(jié)點(diǎn)i到目標(biāo)節(jié)點(diǎn)的估計(jì)成本，式（6）表示啟發(fā)函數(shù)采用基于曼哈頓距離的A*算法，式（7）表示總的等待時(shí)間，式（8）表示AGV的移動(dòng)方式選擇，包括在原地等待或向相鄰節(jié)點(diǎn)移動(dòng)一個(gè)時(shí)間步長，式（9）表示所有AGV完成任務(wù)的總代價(jià)。

2 模型求解

2.1 AGV路網(wǎng)模型建立

本模型采用堆場垂直于碼頭岸線的布局，水平運(yùn)輸設(shè)備不進(jìn)入箱區(qū)，在箱區(qū)的兩端與堆場進(jìn)行作業(yè)交接，設(shè)立4臺(tái)岸橋3個(gè)堆場對自動(dòng)化碼頭布局進(jìn)行模擬仿真，如圖1所示，本文選擇雙向單車道路徑，AGV的移動(dòng)方式包括在原地等待或者向相鄰可通行的四節(jié)點(diǎn)移動(dòng)。其中灰色障礙物表示堆場緩沖區(qū)，在AGV進(jìn)行水平運(yùn)輸作業(yè)時(shí)，將其視為障礙物。

自動(dòng)化碼頭中AGV路徑規(guī)劃系統(tǒng)是由岸橋，堆場，緩沖區(qū)和磁釘?shù)雀鱾€(gè)設(shè)備組成的復(fù)雜系統(tǒng)，針對AGV水平運(yùn)輸區(qū)，使用柵格法對地圖進(jìn)行建模，用單元格將障礙信息表示出來，單元格的權(quán)值是布爾變量，其中可通行的節(jié)點(diǎn)用0表示，不可通行的節(jié)點(diǎn)用1表示，AGV不可以和障礙物單元格重疊。

2.2 AGV沖突類型

隨著AGV數(shù)量的增加和碼頭任務(wù)規(guī)模的擴(kuò)大，AGV在岸橋和堆場的水平運(yùn)輸區(qū)主要產(chǎn)生的沖突類型如下：

a）交叉口沖突。

如圖2（a）所示，當(dāng)AGVi，AGVj從垂直方向向交叉柵格Vm行駛，并且在時(shí)間點(diǎn)t同時(shí)到達(dá)同一柵格點(diǎn)Vm，產(chǎn)生交叉點(diǎn)沖突。考慮其為點(diǎn)沖突（AGVi，AGVj，Vm，t），并且在該沖突二叉樹節(jié)點(diǎn)上分別為AGVi添加約束（AGVi，Vm，t），AGVj添加約束（AGVj，Vm，t）。

b）相向沖突。

如圖2（b）所示，當(dāng)AGVi，AGVj從相反的方向向同一柵格節(jié)點(diǎn)Vn行駛，并且在時(shí)間點(diǎn)t同時(shí)到達(dá)同一柵格點(diǎn)Vn，產(chǎn)生相向沖突。與交叉口沖突類似，將其考慮為點(diǎn)沖突（AGVi，AGVj，Vn，t），并且在沖突二叉樹節(jié)點(diǎn)上分別為AGVi添加約束（AGVi，Vn，t），AGVj添加約束（AGVj，Vn，t）。

c）交換沖突。

如圖2（c）所示，當(dāng)AGVi，AGVj從相反的方向行駛，并且在時(shí)間點(diǎn)t打算交換柵格點(diǎn)Vm，Vn的位置，產(chǎn)生交換沖突。考慮其為邊沖突（AGVi，AGVj，Vm，Vn，t），并且在沖突二叉樹節(jié)點(diǎn)上分別為AGVi添加約束（AGVi，Vm，Vn，t），AGVj添加約束（AGVj，Vm，Vn，t）。

d）AGV故障。

如圖2（d）所示，AGVi發(fā)生故障停在柵格點(diǎn)Vm，而AGVj所規(guī)劃路徑與故障點(diǎn)產(chǎn)生重疊，造成設(shè)備等待，本模型不考慮AGV因故障導(dǎo)致沖突的情況。

2.3 通信交互協(xié)議

針對環(huán)境多變的碼頭水平運(yùn)輸作業(yè)，在本模型中忽略通信延遲問題，采用集中式控制方式，使用一個(gè)中央處理器為所有AGV找到解決方案。AGV在水平運(yùn)輸任務(wù)中不斷運(yùn)動(dòng)并且范圍較廣，因此需要采用無線通信系統(tǒng)來實(shí)現(xiàn)AGV之間的通信。考慮通信成本和任務(wù)運(yùn)行的便捷，本文選擇UDP無線網(wǎng)絡(luò)通信協(xié)議，將AGV和控制臺(tái)的網(wǎng)絡(luò)IP地址設(shè)置在同一IP網(wǎng)段內(nèi)，使用無線Wi-Fi信號(hào)連接到路由器，實(shí)現(xiàn)它們AGV與AGV之間，AGV與控制臺(tái)之間的通信。AGV在接收到任務(wù)后將任務(wù)起點(diǎn)，任務(wù)終點(diǎn)，AGV小車編號(hào)發(fā)送給控制臺(tái)；控制臺(tái)將計(jì)算后的每個(gè)小車的無沖突路徑發(fā)送給各個(gè)小車。

2.4 多AGV沖突規(guī)避策略

自動(dòng)化碼頭上存在點(diǎn)沖突與邊沖突，使用底層基于曼哈頓距離的A*算法為每一臺(tái)AGV搜索出最短路徑后，在上層沖突二叉樹上執(zhí)行搜索，沖突樹上每個(gè)節(jié)點(diǎn)表示一組AGV運(yùn)動(dòng)的約束，包括三部分組成，即一組約束N.constraints、一個(gè)解N.solution和總成本N.cost。

圖3是碼頭AGV沖突實(shí)例，S1，S2表示兩個(gè)岸橋，G1，G2表示兩個(gè)堆區(qū)，每臺(tái)AGV必須計(jì)劃其從岸橋到堆場的完整路徑。AGV1必須從岸橋S1到堆區(qū)G1，AGV2必須從岸橋S2到堆區(qū)G2。兩臺(tái)AGV都有各自長度為3的路徑：AGV1：S1，A1，D，G1;AGV2：S2，B1，D，G2。在時(shí)間步長t2時(shí)他們同時(shí)到達(dá)柵格點(diǎn)D產(chǎn)生沖突，選擇總路徑長度最短的AGV添加約束，選擇AGV1等待一個(gè)時(shí)間點(diǎn)。因此，在本例中，最優(yōu)解N.solution=7。

對應(yīng)的沖突二叉樹如圖4所示，沖突樹的根節(jié)點(diǎn)對應(yīng)的約束集是空的，表示為：N.constraints={}；使用底層的A*算法分別計(jì)算出AGV1和AGV2從岸橋到堆場的初始路徑為：N.solution={（AGV1：S1，A1，D，G1），（AGV2：S2，B1，D，G2）}；由式（9）可知N.cost=6。這些信息都保存在根節(jié)點(diǎn)中。在驗(yàn)證給出的解時(shí)，當(dāng)兩臺(tái)AGV在時(shí)間t2時(shí)都到達(dá)柵格點(diǎn)D時(shí)，會(huì)產(chǎn)生一個(gè)沖突conflict=（AGV1，AGV2，D，t2）。因此根節(jié)點(diǎn)不是目標(biāo)節(jié)點(diǎn)。

生成兩個(gè)子節(jié)點(diǎn)以解決沖突。左子節(jié)點(diǎn)添加約束N.constraints={（AGV1，D，t2）}，而右子節(jié)點(diǎn)添加約束N.constraints={（AGV2，D，t2）}。調(diào)用左子節(jié)點(diǎn)的底層A*搜索，查找在滿足新約束下的最優(yōu)路徑。為此，AGV1必須在A1或S1處等待一個(gè)時(shí)間點(diǎn)，則AGV1新路徑為：{S1，A1，A1，D，G1}，AGV2的路徑在左子節(jié)點(diǎn)中保持不變。左子節(jié)點(diǎn)的總代價(jià)N.cost是7。

類似生成右子節(jié)點(diǎn)，代價(jià)N.cost也是7。兩個(gè)子節(jié)點(diǎn)都被插入到OPEN。在while循環(huán)的下一次迭代中，選擇cost最低的節(jié)點(diǎn)展開，即選擇左子節(jié)點(diǎn)進(jìn)行展開，并驗(yàn)證底層路徑。因?yàn)椴淮嬖跊_突，所以左子節(jié)點(diǎn)被聲明為目標(biāo)節(jié)點(diǎn)，它的解決方案N.solution就是這個(gè)碼頭沖突實(shí)例最優(yōu)解決方案。

2.5 改進(jìn)CBS算法

CBS算法為簡化問題通常只考慮點(diǎn)沖突，而碼頭實(shí)際運(yùn)行時(shí)AGV之間存在點(diǎn)沖突與邊沖突，本文采取改進(jìn)的CBS算法在考慮點(diǎn)沖突的同時(shí)，判斷二叉樹中是否存在邊沖突，并對存在邊沖突節(jié)點(diǎn)的子節(jié)點(diǎn)增加約束，實(shí)現(xiàn)多AGV的無沖突路徑規(guī)劃。流程圖如圖5所示，具體搜索步驟如下：

a）初始化二叉樹根節(jié)點(diǎn)，root.constraints=，root.solution=使用底層A*搜索規(guī)劃的路徑集，root.cost=SIC（root.solution）;

b）把根節(jié)點(diǎn)插入Q列表中;

c）如果Q列表不是空，取出Q中cost最少的節(jié)點(diǎn)設(shè)為當(dāng)前節(jié)點(diǎn);

d）判斷當(dāng)前節(jié)點(diǎn)的N.solution是否存在點(diǎn)沖突與邊沖突;

e）如果沒有沖突，N.solution就是解;

f）如果存在沖突，將當(dāng)前節(jié)點(diǎn)從Q中取出，把當(dāng)前節(jié)點(diǎn)的兩個(gè)子節(jié)點(diǎn)分別添加約束加入Q列表中，循環(huán)c）d）直到求出無沖突的路徑集。

3 算例分析

參照自動(dòng)化碼頭實(shí)際，采用如圖6所示的雙向柵格路網(wǎng)圖［2］，路網(wǎng)布局中Q1～Q10為岸橋位置，D1～D30為堆場箱區(qū)的位置，其中白色柵格為可通行的點(diǎn)，灰色柵格為靜態(tài)障礙物不可通行。采用Python語言編程，在IntelAMD5-2500U CPU @ 2.00 GHz、8 GB內(nèi)存的Windows 10計(jì)算機(jī)上實(shí)現(xiàn)。在本算例中，參數(shù)設(shè)置如下：設(shè)置柵格的長度為2 m，柵格大小為40×40，每臺(tái)AGV的速度不變?yōu)? m/s，AGV的長度為2 m。以岸橋到堆場，堆場到岸橋的運(yùn)作方式選擇起點(diǎn)和終點(diǎn)。

3.1 不同算法在30臺(tái)AGV下的實(shí)驗(yàn)對比及分析

實(shí)驗(yàn)設(shè)置AGV的起點(diǎn)和終點(diǎn)如表2所示，AGV需要在相應(yīng)的岸橋作業(yè)起點(diǎn)避開緩沖區(qū)到達(dá)指定的堆場作業(yè)終點(diǎn)，AGV的起點(diǎn)為10個(gè)岸橋，終點(diǎn)為30個(gè)堆場，實(shí)驗(yàn)設(shè)置多臺(tái)AGV可以同時(shí)占據(jù)岸橋，因此不考慮在岸橋處的點(diǎn)沖突與邊沖突。

本實(shí)例設(shè)置有效時(shí)間為60 s，超出時(shí)間無法求出解視為無效，其中終點(diǎn)不可重復(fù)選擇，在AGV數(shù)量相同時(shí)，為改進(jìn)CBS算法和代價(jià)增長樹算法隨機(jī)分配任務(wù)，設(shè)置相同的起點(diǎn)和終點(diǎn)，在AGV數(shù)量為30臺(tái)時(shí)，必須包含所有起點(diǎn)和所有終點(diǎn)，目的是避免空閑，提高岸橋和堆場的利用率。

基于ICTS算法主要是上層在代價(jià)增長樹上搜索總路徑長度最小的節(jié)點(diǎn)后，在上層成本約束下，下層搜索出有效解決方案。文獻(xiàn)［10］采用基于ICTS算法，在減少運(yùn)算時(shí)間取得明顯效果，但是因?yàn)镮CTS是耦合的方法，在密集環(huán)境中或解決沖突的成本非常高的情況，ICTS是低效的。因此，提出基于改進(jìn)CBS算法，是一種混合方式求解大規(guī)模AGV路徑規(guī)劃問題，能夠生成最優(yōu)方案。

設(shè)置AGV的數(shù)量分別為2～30臺(tái)時(shí)，使用改進(jìn)CBS算法和ICTS算法規(guī)劃多臺(tái)AGV從起點(diǎn)到終點(diǎn)的路徑，分別進(jìn)行10次實(shí)驗(yàn)，為AGV隨機(jī)分配起點(diǎn)終點(diǎn)，分配后的起點(diǎn)終點(diǎn)固定。基于ICTS和改進(jìn)CBS算法在不同AGV數(shù)量下的平均總代價(jià)和平均運(yùn)算時(shí)間如圖7所示。

如圖7（a）所示，比較平均總路徑長度，當(dāng)AGV數(shù)量為2～5時(shí)，AGV數(shù)量較為稀疏，AGV之間沖突較少，ICTS解決沖突的成本較低，求解效果較好，因此兩種算法的總路徑長度相近；而當(dāng)AGV數(shù)量為6～30時(shí)，隨著AGV數(shù)量增加，改進(jìn)CBS算法在二叉樹上選擇總路徑長度最短的節(jié)點(diǎn)，拉大與ICTS算法的差距，兩種算法之間的差距維持恒定。如圖7（b）所示，比較平均運(yùn)算時(shí)間，當(dāng)AGV數(shù)量為2～26臺(tái)時(shí)，兩種算法之間的差距較為平穩(wěn)；當(dāng)AGV數(shù)量為26～30臺(tái)時(shí)，AGV密度增大，ICTS算法采用耦合方式，效率較低，運(yùn)算時(shí)間明顯陡峭上升，而改進(jìn)CBS算法維持較為平穩(wěn)。

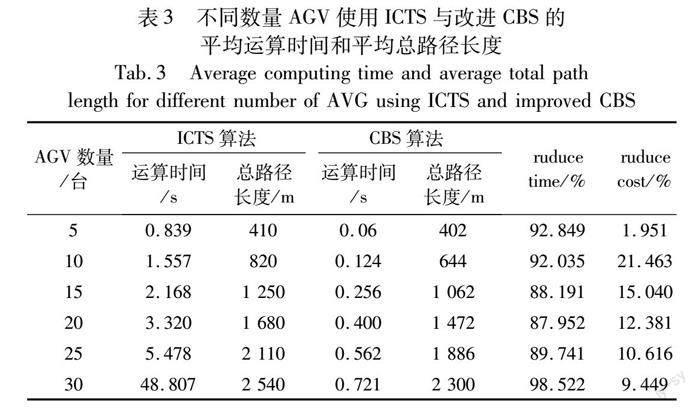
由于兩種算法的平均運(yùn)算時(shí)間和總路徑長度曲線呈單調(diào)遞增的趨勢，選擇AGV數(shù)量為10，20，30臺(tái)時(shí)，比較ICTS與改進(jìn)CBS的運(yùn)算時(shí)間，如圖8所示。選擇AGV數(shù)量為5，10，15，20，25，30臺(tái)時(shí)，比較兩種算法的差距，如圖9和表2所示，其中reduce time=（ICTS算法運(yùn)算時(shí)間-改進(jìn)CBS算法運(yùn)算時(shí)間）/ICTS算法運(yùn)算時(shí)間；reduce cost=（ICTS算法總路徑長度-改進(jìn)CBS算法總路徑長度）/ICTS算法總路徑長度。

如圖8所示，在AGV數(shù)量為10，20，30時(shí)，改進(jìn)CBS算法運(yùn)算時(shí)間明顯低于ICTS。如圖9和表3所示，考慮路徑總長度：a）在AGV=5時(shí)，兩種算法之間的總路徑長度差距為1.951%；b）隨著AGV數(shù)量增加，在AGV=10，15，20，25，30時(shí)，總路徑長度差距增大在9%～22%。符合圖7的分析，而改進(jìn)CBS算法能在沖突二叉樹選擇總路徑長度最短的節(jié)點(diǎn)，總路徑長度明顯低于ICTS算法。

考慮運(yùn)算時(shí)間，a）在AGV=5，10，15，20，25時(shí)，兩種算法運(yùn)算時(shí)間差距維持在88%～92%；b）而隨著AGV數(shù)量增加更加密集，ICTS算法效果較差，運(yùn)算時(shí)間更長，所以當(dāng)AGV數(shù)量=30臺(tái)時(shí)，差距明顯增大為98.522%。基于CBS算法解決沖突時(shí)，只需要對產(chǎn)生沖突的單AGV重新規(guī)劃路徑，而ICTS算法需要對多AGV路徑進(jìn)行驗(yàn)證，運(yùn)算時(shí)間上CBS算法明顯低于ICTS算法。

3.2 改進(jìn)CBS算法在60臺(tái)AGV下的實(shí)驗(yàn)分析

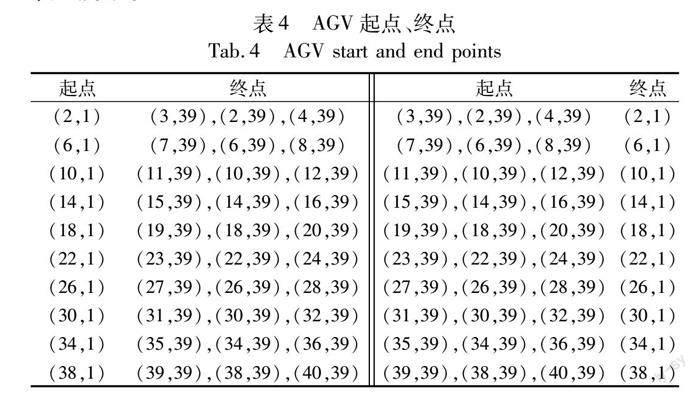
考慮自動(dòng)化碼頭AGV規(guī)模更大的情況，設(shè)置AGV數(shù)量為40，50，60臺(tái)，實(shí)例的有效時(shí)間設(shè)置為60 s，其中起點(diǎn)終點(diǎn)表如表4所示。

隨機(jī)選擇起點(diǎn)和終點(diǎn)，當(dāng)AGV數(shù)量大于30臺(tái)時(shí)，ICTS算法不能在有效時(shí)間內(nèi)求解。使用CBS算法分別進(jìn)行100次實(shí)驗(yàn)，算法有效時(shí)間設(shè)置為60 s，實(shí)驗(yàn)結(jié)果如圖10和表4所示。

運(yùn)算時(shí)間如圖10所示，正方形表示AGV數(shù)量=40，圓形表示AGV數(shù)量=50，三角形表示AGV數(shù)量=60，其中這三種情況總路徑長度分布較為均勻，隨著AGV數(shù)量增加，平均總路徑長度也均勻增加。

如圖10所示，隨著AGV數(shù)量增加，運(yùn)算時(shí)間增加，運(yùn)算時(shí)間過高主要是因?yàn)闆_突二叉樹最小成本的限制，導(dǎo)致求解時(shí)間較長，當(dāng)AGV數(shù)量為40臺(tái)時(shí)，35次實(shí)驗(yàn)?zāi)茉谟行r(shí)間內(nèi)求解，成功率為65%，而AGV數(shù)量為50臺(tái)時(shí)，成功率為14%，AGV數(shù)量為60臺(tái)時(shí)，成功率為2%，主要因?yàn)锳GV數(shù)量增加，密度增大，沖突二叉樹節(jié)點(diǎn)增多，導(dǎo)致計(jì)算時(shí)間過長。如表5所示，在AGV=60臺(tái)時(shí)，能夠在平均運(yùn)算時(shí)間為27.681 s求解無沖突路徑，求得的總路徑長度為6 385.6 m。

為求改進(jìn)CBS算法計(jì)算的最大閾值，設(shè)置AGV數(shù)量為61～65臺(tái)，設(shè)置運(yùn)算時(shí)間超出60 s時(shí)溢出，返回當(dāng)前循環(huán)的運(yùn)算時(shí)間。

如圖11所示，在對61～65臺(tái)的AGV進(jìn)行實(shí)驗(yàn)時(shí)，運(yùn)算時(shí)間均超過60 s，成功率為0%，AGV密度較高超出算法所能計(jì)算的閾值，使用CBS算法難以在60 s有效時(shí)間內(nèi)求解，因此在本模型中使用CBS算法所能解決的AGV數(shù)量最多為60臺(tái)。

4 結(jié)束語

本文以最小化自動(dòng)化碼頭上的AGV總路徑長度為目標(biāo)，考慮AGV之間的點(diǎn)沖突和邊沖突，建立多AGV無沖突路徑規(guī)劃模型，設(shè)計(jì)基于沖突二叉樹的策略解決沖突，使用柵格法建立AGV路網(wǎng)。設(shè)計(jì)基于改進(jìn)CBS算法和ICTS算法的運(yùn)算時(shí)間和總路徑長度的小規(guī)模算例對比實(shí)驗(yàn)，結(jié)果表明當(dāng)AGV數(shù)量為30臺(tái)時(shí)，基于改進(jìn)CBS算法較基于代價(jià)增長樹算法總路徑長度縮短了11.65%，計(jì)算時(shí)間縮短了98.52%；對于大規(guī)模AGV算例，求得改進(jìn)CBS算法計(jì)算自動(dòng)化碼頭多AGV路徑規(guī)劃的閾值為60臺(tái)，能夠在平均運(yùn)算時(shí)間27.681 s求解60臺(tái)。算例結(jié)果驗(yàn)證本算法的有效性，以及改進(jìn)CBS算法更加適合解決60臺(tái)大規(guī)模的AGV無沖突路徑規(guī)劃問題。

本文后續(xù)將在保證路徑無沖突和運(yùn)算質(zhì)量的條件下，對提高運(yùn)算速度進(jìn)行進(jìn)一步研究。

參考文獻(xiàn)：

[1]丁一，袁浩，方懷瑾，等.考慮沖突規(guī)避的自動(dòng)化集裝箱碼頭AGV優(yōu)化調(diào)度方法［J］.交通信息與安全，2022，40（3）：96-107.（Ding Yi，Yuan Hao，F(xiàn)ang Huaijin，et al.An optimal scheduling method for AGVs in automated container terminals considering conflict avoidance［J］.Transportation Information and Safety，2022，40（3）：96-107.）

［2]張其嬌，丁一，秦濤.考慮沖突規(guī)避的自動(dòng)化碼頭多AGV路徑規(guī)劃［J/OL］.計(jì)算機(jī)工程與應(yīng)用.［2023-03-23］.http：//kns.cnki.net/kcms/detail/11.2127.TP.20220705.1751.010.html.（Zhang Qijiao，Ding Yi，Qin Tao.Multi-AGV path planning for automated terminals considering conflict avoidance［J/OL］.Computer Engineering and Applications.［2022-12-17］.http：//kns.cnki.net/kcms/detail/11.2127.TP.20220705.1751.010.html.）

［3]牛雅倩，余芳，劉靜雯，等.基于動(dòng)態(tài)平衡策略的自動(dòng)化碼頭多AGV路徑優(yōu)化算法研究［J］.計(jì)算機(jī)應(yīng)用研究，2022，39（2）：385-390.（Niu Yaqian，Yu Fang，Liu Jingwen，et al.Research on multi-AGV path optimization algorithm for automated terminals based on dynamic balancing strategy［J］.Computer Application Research，2022，39（2）：385-390.）

［4]郭昆侖，朱瑾.基于多智能體系統(tǒng)的自動(dòng)化碼頭多AGV無沖突路徑規(guī)劃［J］.制造業(yè)自動(dòng)化，2021，43（8）：83-89.（Guo Kunlun，Zhu Jin.Conflict-free path planning for multi-AGVs in automated terminals based on multi-intelligent body system［J］.Manufacturing Automation，2021，43（8）：83-89.）

［5]蘭培真，陳錦文，曹士連.基于Ant-agent的自動(dòng)化碼頭AGV控制算法［J］.交通運(yùn)輸系統(tǒng)工程與信息，2020，20（1）：190-197.（Lan Peizhen，Chen Jinwen，Cao Shilian.Ant-agent-based control algorithm for automated terminal AGVs［J］.Transportation Systems Engineering and Information，2020，20（1）：190-197.）

［6]曾慶成，李明澤，薛廣順.考慮擁堵因素的自動(dòng)化碼頭多AGV無沖突動(dòng)態(tài)路徑規(guī)劃模型［J］.大連海事大學(xué)學(xué)報(bào)，2019，45（4）：35-44.（Zeng Qingcheng，Li Mingze，Xue Guangshun.A conflict-free dynamic path planning model for multi-AGVs at automated terminals considering congestion factors［J］.Journal of Dalian Maritime University，2019，45（4）：35-44.）

［7]Zhong Meisu，Yang Yongsheng，Dessouky Y，et al.Multi-AGV scheduling for conflict-free path planning in automated container terminals［J］.Computers & Industrial Engineering，2020，142：106371.

［8]Yue Lijun，F(xiàn)an Houming.Dynamic scheduling and path planning of automated guided vehicles in automatic container terminal［J］.IEEE/CAA Journal of Automatica Sinica，2022，9（11）：2005-2019.

［9]Goldenbnberg M，F(xiàn)elner A，Stern R，et al.Enhanced partial expansion A*［J］.Journal of ArtificialIntelligence Research，2014，50（1）：141-187.

［10]Sharon G，Stern R，Goldenberg M，et al.The increasing cost tree search for optimal multi-agent pathfinding［J］.Artificial intelligence，2013，195：470-495.

［11]Surynek P.Towards optimal cooperative path planning in hard setups through satisfiability solving［C］//Proc of Pacific Rim International Conferenceson Artificial Intelligence.Piscataway，NJ IEEE Press，2012：564-576.

［12]Sharon G，Stern R，F(xiàn)elner A，et al.Conflict-based search for optimal multi-agent pathfinding［J］.Artificial Intelligence，2015，219：40-66.

［13]Hnig W，Kiesel S，Tinka A，et al.Persistent and robust execution of mapf schedules in warehouses［J］.IEEE Robotics and Automation Letters，2019，4（2）：1125-1131.

［14]黃鼎勇，周芳，路遙，等.基于沖突搜索的數(shù)字戰(zhàn)場多無人機(jī)路徑規(guī)劃與仿真［J］.指揮信息系統(tǒng)與技術(shù)，2022，13（4）：32-39.（Huang Dingyong，Zhou Fang，Lu Yao，et al.Conflict search-based path planning and simulation of multiple UAVs on digital battlefield［J］.Command Information Systems and Technology，2022，13（4）：32-39.）

［15]郭超，陳香玲，郭鵬，等.基于時(shí)空A～*算法的多AGV無沖突路徑規(guī)劃［J］.計(jì)算機(jī)系統(tǒng)應(yīng)用，2022，31（4）：360-368.（Guo Chao，Chen Xiangling，Guo Peng，et al.Conflict-free path planning for multiple AGVs based on spatio-temporal A～* algorithm［J］.Computer Systems Applications，2022，31（4）：360-368.）

［16]劉恒麟.多AGV路徑規(guī)劃算法的研究與實(shí)現(xiàn)［D］.南京：東南大學(xué)，2020.（Liu Henglin.Research and implementation of multi-AGV path planning algorithm［D］.Nanjing：Southeast University，2020.

收稿日期：2023-02-12；

修回日期：2023-03-29

基金項(xiàng)目：國家自然科學(xué)基金資助項(xiàng)目（62073212）

作者簡介：周欣慈（2000-），女，安徽淮北人，碩士研究生，主要研究方向?yàn)锳GV路徑規(guī)劃；朱瑾（1980-），女（通信作者），湖北武漢人，副教授，碩導(dǎo)，博士，主要研究方向?yàn)楦劭谧詣?dòng)化、生產(chǎn)與物流建模與優(yōu)化（jinzhu@shmtu.edu.cn）.