量子近似優化算法在最大獨立集中的應用

段孟環 李志強 郭玲玲

摘 要：最大獨立集問題是著名的NP問題，并且在許多場景中都有應用。傳統的精確算法解決最大獨立集問題需要指數級的時間復雜度。為更高效地解決最大獨立集問題，提出了一種基于量子近似優化算法的量子線路解決方案。該方案由最大獨立集的數學模型，推導出最大獨立集問題的哈密頓量表達式；設計了基于量子近似優化算法的量子線路，采用COBYLA經典優化算法對參數量子門中的參數進行優化，并使用IBM提供的量子開發框架Qiskit進行仿真實驗。仿真結果表明，使用量子近似優化算法可以在多項式時間以高概率內獲得最大獨立集問題的解，實現了指數加速。量子近似優化算法對解決最大獨立集問題有一定的可行性和有效性。

關鍵詞：最大獨立集； 量子近似優化算法； 量子線路； Qiskit

中圖分類號：O4?? 文獻標志碼：A

文章編號：1001-3695（2023）09-013-0000-00

doi：10.19734/j.issn.1001-3695.2023.02.0031

Application of quantum approximate optimization algorithm in

max independent set problem

Duan Menghuan， Li Zhiqiang， Guo Lingling

（College of Information Engineering， Yangzhou University， Yangzhou Jiangsu 225100， China）

Abstract：The max independent set problem is a well-known NP problem and has applications in many scenarios. Traditional exact algorithms need exponential time complexity to solve the max independent set problem. In order to solve the max independent set problem more efficiently， this paper proposed a quantum circuit solution based on the quantum approximate optimization algorithm. In this scheme， derived the Hamiltonian expression of the max independent set problem from the mathematical model of the max independent set， designed the quantum circuit based on the quantum approximation optimization algorithm. It used the COBYLA classical optimization algorithm to optimize the parameters in the parameter quantum gate， and used the quantum development framework Qiskit provided by IBM to conduct simulation experiments. Simulation results show that the solution of the max independent set problem can be obtained in polynomial time with high probability using the quantum approximate optimization algorithm， achieving an exponential speedup. Quantum approximate optimization algorithm is feasible and effective for solving the max independent set problem.

Key words：max independent set problem; quantum approximate optimization algorithm; quantum circuit; Qiskit

0 引言

1972年，Karp提出了21個NP完全問題［1］，最大獨立集問題（max independent set problem，MISP）就是其中之一。最大獨立集問題是一個經典的組合優化問題［1，2］，數十年來受到了大量學者的關注，并且將其應用于各個場景中［3，4］。文獻[5，6]提出了一系列基于分支定界策略（branch and bound strategy）的精確算法來解決最大獨立集問題，這些精確算法解決最大獨立集問題需要指數級的時間。

隨著量子計算［7～9］的發展，量子計算有望成為一種具有顛覆性影響的計算方式。量子計算基于量子態的連貫性和糾纏性，可以輕松完成并行計算。某些在經典處理器上難以解決的問題，在量子處理器上可以實現指數加速或二次加速［10，11］。2014年，Farhi等人［12］提出了量子近似優化算法（quantum approximate optimization algorithm，QAOA）并將其應用于解決最大割問題。量子近似優化算法是一種啟發式的量子經典混合算法，主要用于解決組合優化問題。相比于經典算法，量子近似優化算法對解決組合優化問題有指數加速。根據相關文獻［13，14］，量子近似優化算法是在近期的量子計算機上實現的最有前途的顯示量子優勢的算法之一。近年來，量子近似優化算法被用于精確覆蓋［15］、漢密爾頓路［16］、背包問題等問題［17］。

在本文中，提出了一種基于量子近似優化算法的量子線路解決方案用于解決最大獨立集問題。首先，根據最大獨立集問題的數學模型構建相應的二次無約束二元優化（quadratic unconstrained binary optimization，QUBO）模型。其次，根據量子系統理論，由QUBO模型推導出量子Ising模型和問題哈密頓量。第三，基于QAOA原理，得到基于初始哈密頓量和問題哈密頓量的參數酉變換。參數主要與量子門的旋轉角度有關。交替使用酉變換可以得到最終的量子態。最后，根據初始量子態和參數酉變換設計量子門，生成可以在量子計算機上執行的量子線路。在演化過程中，采用經典優化算法對量子線路的參數進行優化，通過調整問題的哈密頓量的期望，從而提高解的概率。該方案可以有效地解決最大獨立集問題。

1 問題模型

在無向圖G=（V，E）中，其中V表示無向圖G的頂點集，E表示無向圖G的邊集。

圖G=（V，E）中兩兩互不相鄰的頂點構成的集合稱為獨立集。最大獨立集是具有最大尺寸的獨立集。

假設S是無向圖G=（V，E）的獨立集。|S|表示獨立集中頂點的個數。最大獨立集問題的目標函數可以由F1表示，其中xi對應于第i個頂點的取值，當vi∈S時，xi=1；viS時，xi=0。

3 仿真與結果分析

使用QAOA解決最大獨立集問題時，首先需要將圖的頂點映射至量子比特。然后根據圖中的邊和第2章中所示方案生成QAOA量子線路，對量子比特進行測量并計算哈密頓量的期望值，在經典部分使用經典參數優化器對量子線路中的參數進行優化。重復上述步驟，直到收斂。最終得到的量子比特的測量值組成的字符串就是最大獨立集所對應的解。本文對圖3中的示例進行實驗仿真。因為該示例有6個頂點，在初始化時需要準備6個量子比特，每個量子比特對應于一個頂點。然后根據第三部分的內容構造量子線路。最后對最終狀態進行測量可以得到由“0”和“1”組成的6位字符串，其中“0”表示該頂點未被選中，“1”表示該頂點被選中。算法1給出了該方案的主要偽代碼。

算法1 基于QAOA的最大獨立集算法

輸入：無向圖G=（V，E），演化步數p。

輸出： 最優解S。

nqubits←|V|

qc←QuantumCircuit（nqubits） //初始化量子線路

γ，β←1.0 ?//初始化2p個參數

for i←0： nqubits do //制備初始疊加態

qc.h（i）

end for

while stop criterion is no satisfied do

for k←1：p do

qc.append（U（HC，γk）） //式（17）

qc.append（U（HM，βk）） //式（20）

end for

計算期望值Fp（γ，β） //式（11）

使用經典優化器優化參數γ和β

end while

測量量子態

S←具有最高概率的量子態對應的比特串

輸出S

3.1 仿真結果與分析

本文主要使用IBM開發的量子軟件開發工具Qiskit［22］在Python 3中模擬和實現所設計的量子線路。可以知道，圖3中的示例，其最大獨立集S={0，1，4，5}。相應地，在QAOA下，獲得字符串“110011”的概率應該最大。本文選取了演化步數為1至11進行仿真實驗。

在使用QAOA求解圖2的最大獨立集時，在不限制迭代次數的情況下，當演化步數為1～11時，得到正確解“110011”的概率如圖5所示。

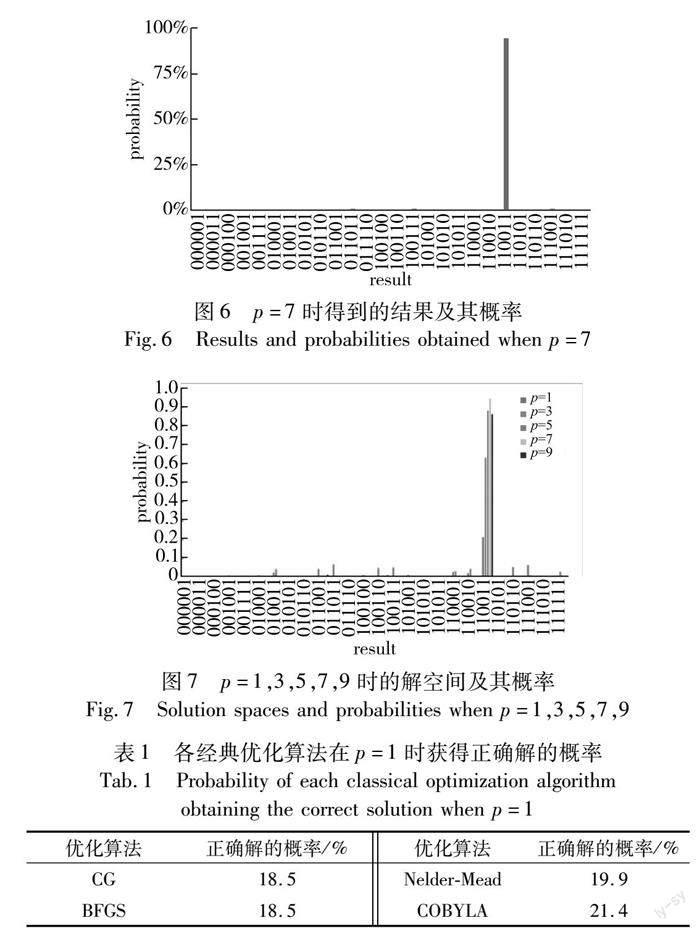
從圖5可以看出，當p=1時，QAOA算法獲得正確解的概率為21.4%，當p=2時，獲得正確解的概率顯著增加，并且隨著演化步數的增加，獲得的問題解的正確率總體呈現上升趨勢。但并不是所有的演化結果都比之前的演化結果好，它是會有波動的。在達到一定數量的進化步驟后，其正確率可能會下降，但仍保持在較高水平，這與文獻［12］的結論一致。從圖4可以看出，當演化步數p為1到11時，在p=7時的結果最好，正確率達到94.5%。

圖6顯示了當p=7時，QAOA算法所得到的結果及其對應的概率。圖7給出了在p=7的結果空間下，p分別為1，3，5，7，9時獲得各個結果的概率。

從圖7中可以看出，當演化步數p為3， 5， 7， 9時，正確解的概率非常顯著。因此，結果表明，本文提出的基于QAOA的解決方案可以用于解決最大獨立集問題。

3.2 迭代與優化結果與分析

在實驗過程中，為了使QAOA得到較好的結果，需要在經典計算部分采用優化算法來優化參數（γ，β）以得到較優的（γ，β）。常用的優化方法有CG算法［23］、BFGS算法［24］、Nelder-Mead算法［25］和COBYLA算法［26］等。各經典優化算法在p=1時，獲得正確解的概率如表1所示。可以看出，使用COBYLA經典優化算法能以更高的概率獲得正確解。因此，本文使用COBYLA經典優化算法來優化參數（γ，β）。

圖8顯示了當演化步數為1到11時，經典優化算法COBYLA獲得最佳參數所需的迭代次數。可以看出，隨著演化步數的增加，所需迭代次數也會增加。因為所需要優化的參數的數量會隨著演化步數的增加而增加，參數的優化更加復雜，獲得最優參數的迭代次數也會增加。

圖8顯示了當演化步數為1到11時，經典優化算法COBYLA獲得最佳參數所需的迭代次數。可以看出，隨著演化步數的增加，所需迭代次數也會增加。因為所需要優化的參數的數量會隨著演化步數的增加而增加，參數的優化更加復雜，獲得最優參數的迭代次數也會增加。

圖9顯示了當演化步數為1，3，5，7，9時，隨著迭代次數的增加，損失值的變化過程。從圖9可以看出，在演化步數一定時，迭代次數越多，損失值的絕對值越大。但在達到某個值后，損失值變化很小或根本沒有變化。這是因為當目標函數接近局部最優解或目標函數已達到最優且優化已完成時，目標函數的收斂速度減慢。當演化步數分別為5和9時，它們的損失值相差不大，圖5的結果也表明它們之間的差異僅為1.9%。因此，當獲得正確解的概率相差不大時，本文可以優先選擇較少的演化步數，同時選擇適當的迭代次數，以節省時間和空間開銷。

3.3 QAOA復雜度分析

本文采用混合量子—經典算法QAOA求解最大獨立集問題。它主要包括兩部分：經典處理器部分和量子處理器部分。在經典處理器中，使用COBYLA算法來優化參數。COBYLA算法的時間復雜度是O（poly（m）），其中m是迭代次數，可以自己設置。poly（m）是m的多項式函數，這意味著COBYLA算法的計算復雜度是多項式級別的。在量子處理器中，主要完成量子態從量子初始態到量子最終態的演化，并測量量子最終態。結合相關文獻［27］，量子態的演化是最耗時的，幾乎相當于整個量子電路的時間復雜度。因此，量子部分的時間復雜度是O（poly（p）），為多項式級別，其中p演化步數。因此，本文提出的量子線路求解方案的時間復雜度為O［poly（m）+poly（p）］。而求解最大獨立集問題的精確算法的時間復雜度是指數級的。由此，可以得出結論，基于QAOA的求解算法的時間復雜度優于傳統的求解算法，尤其是當問題規模較大時。

4 結束語

本文針對最大獨立集問題，提出了一種基于QAOA量子線路的解決方案。根據最大獨立集問題的性質，建立了最大獨立集的問題模型。推導出了最大獨立集的問題哈密頓量，并且根據其哈密頓量，設計了一個基于QAOA的量子線路，使用經典優化算法來優化參數，并在IBM開發的Qiskit框架中進行了仿真。仿真結果表明，本文提出的基于QAOA算法的量子線路求解方案能夠有效地獲得最大獨立集問題的解。與經典的精確算法相比，本文方案實現了指數加速，大大提高了效率。

本文提出的方案仍需改進，主要包括兩個方面：

a）經典優化器的優化效果不太理想;b）可以進一步優化所設計的量子線路。

為了解決上述兩個問題，今后主要關注以下工作：a）研究參數酉變換的參數特性，選擇或設計一個更好的經典優化器，以提高優化效率和效果;b）設計一個QAOA線路的編譯方案用于優化QAOA的線路，減少量子門的數量，提高QAOA線路的執行效率。

參考文獻：

[1]Karp R M，Miller R E，Thatcher J W.Reducibility among combinatorial problems［J］.The Journal of Symbolic Logic，1975，40：618-619.

［2]Shen Yunzhuang，Sun Yuan，Li Xiaodong，et al.Multi-shot solution prediction for combinatorial optimization［EB/OL］.（2022）［2023-03-31］.https：//arxiv.org/abs/2204.08700.

［3]Li Lianjie，Huang Wenqian，Wang Zheli，et al.Calibration transfer between developed portable Vis/NIR devices for detection of soluble solids contents in apple［J］.Postharvest Biology and Technology，2022，183：111720.

［4]Davoudi M，Moosavi M R，Sadreddini M H.DSS：a hybrid deep model for fake news detection using propagation tree and stance network［J］.Expert Systems with Applications，2022，198：116635.

［5]Dai Jinyu，Wu Zhengtia，Karimi H R，et al.An approximation lagrangian-based algorithm for the maximum clique problem via deterministic annealing neural network［J］.Journal of the Franklin Institute，2022，359（12）：6080-6098.

［6]Forget N，Gadegaard S L，Klamroth K，et al.Branch-and-bound and objective branching with three or more objectives［J］.Computers & Operations Research，2022，148：106012.

［7]Zhong Hansen，Wang Hui，Deng Yuhao，et al.Quantum computational advantage using photons［J］.Science，2020，370（6523）：1460-1463.

［8]Arute F，Arya K，Babbush R，et al.Quantum supremacy using a programmable superconducting processor［J］.Nature，2019，574（7779）：505-510.

［9]李曉巍，付祥，燕飛，等.量子計算研究現狀與未來發展［J］.中國工程科學，2022，24（4）：133-144.（Li Xiaowei，Fu Xiang，Yan Fei，et al.Current status and future development of quantum computation［J］.Strategic Study of CAE，2022，24（4）：133-144.）

［10]Ahnefeld F，Theurer T，Egloff D，et al.Coherence as a resource for Shors algorithm［J］.Physical Review Letters，2022，129（12）：120501.

［11]吳希，李志強，楊東晗.Grover量子搜索算法的線路優化［J］.計算機工程與科學，2023，45（3）：420-425.（Wu Xi，Li Zhiqiang，Yang Donghan.Circuit optimization of Grover quantum search algorithm［J］.Computer Engineering & Science，2023，45（3）：420-425.）

［12]Farhi E，Goldstone J，Gutmann S.A quantum approximate optimization algorithm［EB/OL］.（2014）［2022-05-31］.http：//arxiv.org/abs/1411.4028.

［13]Bechtold M，Barzen J，Leymann F，et al.Investigating the effect of circuit cutting in QAOA for the MaxCut problem on NISQ devices［EB/OL］.（2023）［2023-03-31］.https：//arxiv.org/abs/2302.01792.

［14]Preskill J.Quantum computing in the NISQ era and beyond［J］.Quantum，2018，2：79.

［15]Vikstl P，Grnkvist M，Svensson M，et al.Applying the quantum approximate optimization algorithm to the tail-assignment problem［J］.Physical Review Applied，2020，14（3）：034009.

［16]Gong Changqing，Wang Ting，He Wanying，et al.A quantum approximate optimization algorithm for solving Hamilton path problem［J］.The Journal of Supercomputing，2022，78（13）：15381-15403.

［17]Roch C，Impertro A，Phan T，et al.Cross entropy hyperparameter optimization for constrained problem Hamiltonians applied to QAOA［C］// Proc of International Conference on Rebooting Computing.Piscataway，NJ：IEEE Press，2020：50-57.

［18]Lucas A.Ising formulations of many NP problems［J］.Frontiers in Physics，2014，2：5.

［19]Schmitt M，Rams M M，Dziarmaga J，et al.Quantum phase transition dynamics in the two-dimensional transverse-field Ising model［J］.Science Advances，2022，8（37）：eabl6850.

［20]Choi J，Oh S，Park S，et al.Proper cost hamiltonian design for combinatorial optimization problems：a boolean function approach［C］//Proc of International Conference on Information Networking.Piscataway，NJ：IEEE Press，2021：469-472.

［21]Majumdar R，Bhoumik D，Madan D，et al.Depth optimized ansatz circuit in QAOA for max-cut［EB/OL］.（2021）［2022-06-30］.https：//arxiv.org/abs/2110.04637.

［22]https：//qiskit.org/［EB/OL］.

［23]Wasi H A，Shiker M A K.Proposed CG method to solve unconstrained optimization problems［J］.Journal of Physics：Conference Series，2021，1804（1）：012024.

［24]Liu Qiancheng，Beller S，Lei Wenjie，et al.Pre-conditioned BFGS-based uncertainty quantification in elastic full-waveform inversion［J］.Geophysical Journal International，2022，228（2）：796-815.

［25]Liu Yun，Chong Guoshuang，Heidari A A，et al.Horizontal and vertical crossover of Harris hawk optimizer with Nelder-Mead simplex for parameter estimation of photovoltaic models［J］.Energy Conversion and Management，2020，223：113211.

［26]Pellow-Jarman A，Sinayskiy I，Pillay A，et al.A comparison of various classical optimizers for a variational quantum linear solver［J］.Quantum Information Processing，2021，20（6）：202.

［27]Zhou L，Wang Shengtao，Choi S，et al.Quantum approximate optimization algorithm：Performance，mechanism，and implementation on near-term devices［J］.Physical Review X，2020，10（2）：021067.

收稿日期：2023-02-16；

修回日期：2023-04-03

基金項目：國家自然科學基金資助項目（61070240，62071240）；江蘇省高校基金資助項目（10KJB520021）

作者簡介：段孟環（2000-），女，湖南衡陽人，碩士研究生，主要研究方向為量子算法、量子電路；李志強（1974-），男（通信作者），江蘇揚州人，教授，碩導，博士研究生，主要研究方向為量子計算、量子可逆電路（yzqqlzq@163.com）；郭玲玲（1999-），女，江蘇鹽城人，碩士研究生，主要研究方向為量子算法、量子電路.