多策略融合改進的自適應被囊群算法

柴巖 李廣友 任生 許兆楠

摘 要：針對被囊群算法全局搜索不充分和易陷入局部極值等問題，提出一種多策略融合改進的自適應被囊群算法（MITSA）。首先，在種群初始化中引入佳點集理論提升種群多樣性；其次，提出一種多精英協同引導機制優化被囊個體位置信息，增大對未知搜索區域的勘探可能性以增強算法全局探索能力；然后將自適應權重因子引入群體行為階段，動態平衡算法的全局與局部搜索性能；接著，為增強算法的抗停滯能力，采用依概率小波變異策略實現個體動態微調，同時利用貪婪原則保留優異信息助推種群向食物源靠近；最后基于Markov鏈理論對改進算法的全局收斂性進行分析論證。通過對基準測試函數和CEC2014復雜函數進行數值仿真，實驗結果與Wilcoxon秩和檢驗結果綜合驗證了MITSA具有優越的收斂精度、穩健的魯棒性和高維可拓展性。

關鍵詞：被囊群算法； 佳點集； 多精英協同引導； 自適應權重； 小波變異

中圖分類號：TP18?? 文獻標志碼：A

文章編號：1001-3695（2023）09-021-2694-10

doi：10.19734/j.issn.1001-3695.2023.02.0016

Multi-strategy fusion improved adaptive tunicate swarm algorithm

Chai Yan， Li Guangyou， Ren Sheng， Xu Zhaonan

（College of Science， Liaoning Technical University， Fuxin Liaoning 123000， China）

Abstract：In order to solve the problems of inadequate global search and easy to fall into local extremum， this paper proposed a multi-strategy fusion improved adaptive tunicate swarm algorithm（MITSA） . Firstly， this paper used the best point set strategy to improve population diversity during initialization. Secondly， it offered a multi-elite cooperative guidance mechanism to optimize the tunicates location information， and enhance the global exploration ability of the algorithm by increasing the exploration possibility of unknown search area. Then， the algorithm achieved dynamic global and local search balance by introducing adaptive weight factors into the group behavior stage. Meanwhile， probabilistic wavelet variation strategy promoted individual dynamic fine-tuning to enhance the anti-stagnation ability of the algorithm， while using the greedy principle to retain excellent information to help the population to the food source. Finally， this paper proved the global convergence of the improved algorithm based on Markov chain theory. Through the numerical simulation of the benchmark test function and CEC2014 complex function， the experimental results and Wilcoxon rank sum test results comprehensively verify MITSAs excellent convergence accuracy， robust robustness and high-dimensional scalability.

Key words：tunicate swarm algorithm（TSA）; good point set; multi-elite collaborative guidance; adaptive weight; wavelet mutation

0 引言

被囊群算法（TSA）［1］作為一種新型元啟發式算法，是由Kaur等人啟悟于被囊動物獨特的噴氣式推進行為和集群覓食行為構建并提出的，該算法是基于無梯度的優化技術，具有原理簡單、參數少、局部開發能力強的優勢。文獻［1］的研究表明，TSA的尋優能力明顯優于粒子群算法（particle swarm optimization， PSO）［2］、遺傳算法（genetic algorithm， GA）［3］等經典智能優化算法，與正余弦算法（sine cosine algorithm， SCA）［4］、灰狼優化算法（grey wolf optimizer， GWO）［5］、斑點鬣狗優化算法（spotted hyena optimizer， SHO）［6］、帝企鵝優化算法（emperor penguin optimizer， EPO）［7］等新型元啟發式算法相比，TSA也有較強的競爭力［1］。

自TSA提出以來，已經被廣泛應用到調度優配、參數提取、圖像閾值分割、通信資源分配等實際問題中［8～12］。然而，TSA在求解高維復雜優化問題時存在易陷入局部最優、收斂精度低等缺點。鑒于此，許多研究學者聚焦于開發性能更好且具有實際應用場景的TSA變體。

Houssein等人［13］將TSA與局部逃逸算子相結合，防止系統的搜索緊縮；Fetouh等人［14］引入萊維航班分布增強TSA的多樣化搜索能力，并將所提改進算法成功應用于配電系統性能提升問題中；文獻［15］利用tent映射生成初始種群，采用灰狼優化器生成全局搜索向量，并引入Lévy飛行擴大算法搜索范圍；文獻［16］將整個種群分為兩個子群，分別執行信息共享搜索和噴氣推進搜索，提升了種群多樣性；文獻［17］在標準TSA基礎上引入黃金正弦算法，對被囊種群的噴氣推進與群體行為進行改進以提高種群多樣性及其質量；文獻［18］引入Singer映射于種群初始化提高算法收斂速度，并通過參數位置自適應調節被囊個體與最優被囊個體位置使算法跳出局部最優，并將改進算法成功用于求解露天礦無人駕駛卡車運輸調度優化問題。

上述文獻采用不同策略彌補TSA的缺陷并取得了一定成效，但TSA的尋優性能和收斂精度仍有待進一步提升。因此，本文提出了一種多策略融合改進的自適應被囊群算法（multi-strategy fusion improved adaptive TSA，MITSA）。首先，采用佳點集法生成初始種群以提升種群的均勻遍歷性；其次在個體位置更新階段，設計多種群協同引導搜索機制增大算法對未知搜索區域的搜索范圍，有效提升算法全局搜索能力；同時，在被囊動物的群體行為階段引入自適應權重因子，動態調控算法的全局與局部搜索能力并加速算法收斂；然后對群體行為后的個體進行依概率小波變異擾動，增強算法局部最優逃逸能力。最后基于馬爾可夫鏈理論證明本文算法依概率1收斂于全局最優解，并通過四組數值實驗驗證了MITSA算法的尋優精度、收斂速度、穩定性均取得了較大提升。

1 被囊群算法

TSA是基于被囊動物覓食行為而提出的一種全局搜索算法。被囊動物是一種以流體噴氣式推進力在海洋中移動的動物，具有在深海中覓食的能力，但由于被囊動物多數只有幾毫米大，在食物搜尋后期常借用膠狀被膜相互連接并利用一種淺藍綠色的光散發信號，采取集群方式獲得食物。受被囊動物覓食行為的啟發，被囊群算法采用噴氣式推進和群體行為兩種策略建模，其中噴氣推進主要由三部分組成：避免搜索個體沖突，向最優搜索鄰居移動和向最優搜索個體收斂，群體行為主要為更新最優搜索個體位置。在迭代搜索過程中，被囊個體代表優化問題的可行解，食物代表問題的最優解。

3 仿真實驗與結果分析

3.1 實驗設計

為測試MITSA優越的尋優性能，共進行四組實驗：實驗1為消融實驗探究各策略對TSA性能改善的有效性；實驗2與新近元啟發式算法對比，驗證MITSA優越的尋優精度和優良的收斂速度；實驗3通過Wilcoxon 非參數檢驗，進一步從統計學角度分析MITSA優異的高精度收斂性能；實驗4在CEC2014測試函數上說明MITSA對復雜問題的優化適用性和強健的穩定性。

選取新型原智能優化算法ChoA［22］、HHO［29］和新近改進算法IWOA［30］、GEN-SOA［31］、SOM-KADE［32］、ISMTSA［16］、EGTSA［17］為對比算法，多角度選擇對比算法旨在更全面地驗證MITSA的性能，證明其優勢。按單峰、多峰、固定維度函數為1∶1∶1的比例選取12個常用的基準測試函數，其中f1～f4為單峰函數，測試算法的尋優精度能力和收斂速度；f5～f8為復雜多峰函數，檢驗算法的勘探與開采能力；f9～f12為固定維度多峰函數，具有強烈的振蕩特征，詳細描述如表1所示。仿真實驗系統為64位的Windows 10，CPU為Intel CoreTM i5-6200U，主頻2.30 GHz，內存為8 GB，實驗平臺為 MATLAB R2017a。

3.2 各改進策略有效性分析

3.2.1 參數分析

為研究多精英協同引導機制中狀態池容量大小m對TSA全局搜索性能的差異性影響，設定最大容量為種群數量的一半，即以候選個體m∈{1，2，3，…，15}分別在基準測試函數上進行實驗，相應算法記為TSA-CI m。設置實驗參數種群規模N=30和最大迭代次數T=500，單多峰函數維度d=30。為保證算法性能評價的客觀性，各實驗獨立運行30次并以其逐代平均適應度值繪制算法性能對比曲線見圖3。

由圖3可知，TSA-CI m算法尋優精度隨候選個體的不同變化趨勢均呈現非線性變化。其中，當候選個體m取值較小時，種群多樣性不高，收斂精度得不到明顯提升；在m=5時TSA-CI m算法性能表現較好，可獲得相對最佳尋優精度；隨著候選個體m的增大，狀態池結構相對復雜，影響了算法的運算速度和尋優效率，入選者xeq的位置不具優勢。因此，為平衡算法的尋優速度和優化性能，本文選用m=5并作后續MITSA實驗的設置。

3.2.2 各改進策略對性能影響分析

為驗證四種改進策略及貪婪原則對被囊群算法性能提升的有效性，本文設置僅融合佳點集策略的改進被囊群算法為MITSA-1、僅融合多精英協同引導機制的改進被囊群算法為MITSA-2、僅融合自適應權重因子的改進被囊群算法為MITSA-3、僅融合依概率小波變異策略的改進被囊群算法為MITSA-4、無貪婪原則的多策略融合改進的自適應被囊群算法為MITSA-5。實驗參數設置同3.2.1節，并對基準測試函數進行30次尋優處理，其結果平均值與標準差對比如表2所示，表中加粗數字表示每個函數各指標的最優值。

由表2可知，本文提出的佳點集策略、多精英協同引導機制、自適應權重策略和依概率小波變異策略對標準TSA的尋優性能提升均有一定的幫助，貪婪原則有利于提升種群整體質量。其中，MITSA-1在各測試函數上的表現良好，且在復雜多峰函數和固定維度函數上的表現更優于簡單的單峰函數，體現出了初始種群質量提升對算法尋優的積極影響。MITSA-2的指標值在TSA的基礎上提升多至數百個單位，且相對于MITSA-1、MITSA-3、MITSA-4，其精度優勢突出，這表明采用多精英協同引導機制的被囊群算法提升了TSA的全局搜索性能且能夠很好地滿足前期以全局搜索為主，后期以局部開采為主的尋優規律；同時，MITSA-2與MITSA的收斂精度相對接近，證明了該策略在算法精度提高中有著顯著貢獻。MITSA-3相較標準TSA的尋優能力具有明顯增強，佐證了自適應權重在算法協調全局與局部搜索能力中的重要作用。MITSA-4的指標值在各基準測試函數上均優于TSA的指標值，特別地，在函數f7與f11上，MITSA-4均可收斂到全局最優值，說明對于多極值且不易尋得理論最優解的復雜函數，依概率小波變異策略能夠幫助算法及時跳出局部最優從而尋得理論最優解或相對全局最優解。MITSA-5的收斂精度較MITSA受到了顯著影響，這驗證了貪婪原則在引導被囊種群進化方向上起著重要作用，從而助推種群向食物源靠近。同時，MITSA具有最優的收斂精度和魯棒性，從而綜合證明了四種改進策略對標準TSA的有效改進。

3.3 MITSA算法與其他新近元啟發式算法性能對比

為驗證MITSA優越的尋優性能，對比分析MITSA算法與各對比算法在測試函數上的尋優情況。實驗種群規模N和最大迭代次數T分別為30、500，單峰、多峰測試函數維度分別設置為50/500/1000，固定維度函數的維度參照表1，各算法的其他參數設置如同原文獻。30次獨立實驗的單多峰測試函數結果如表3所示，固定維度函數實驗結果如表4所示。

表3中，首先進行縱向分析可知， MITSA相對于其他六種對比算法各項評價指標均表現最優，甚至在單峰測試函數上30次獨立實驗的最優值和平均最優值指標均已經高出其他對比算法數十個乃至上百個數量級；對于復雜多峰測試函數，MITSA的尋優能力同樣突出，其中，對于存在大量極值點的函數f5，各算法中僅有MITSA收斂到了函數理論最優值-20 945附近。

由表橫向分析可知，不同函數維度下的算法尋優精度不同，在保持進化次數（N×T）不變的情況下，隨著維度的增大，各算法的尋優精度均逐漸下降，其歸因于維度的增大使得種群搜索范圍變大，進而影響算法的搜索精度；但無論在50d、500d維還是1 000d的高維實驗中，改進算法MITSA均能求解出基準測試函數當前迭代次數下的全局最優解并始終保持各項指標最優，證明了ITSA卓越的尋優競爭力和優異的高維問題適用性。

表4中，對于固定維度測試函數，MITSA基本都能收斂到理論值附近，且在測試函數f9、f11～f12上均能收斂到理論最優值，且在各函數上的方差與最劣值均表現最佳，表明MITSA具有良好的高振蕩適應性，且在極端情境中仍保持較高精度收斂。

為更加直觀地觀測各算法的收斂速度、尋優穩定性和局部最優逃逸能力等情況，根據d=50的單多峰函數和固定維度函數的實驗數據分別對各算法的收斂情況進行可視化，其收斂曲線對比如圖4所示。

由于MITSA收斂精度高，所以對適應度值取10為底的對數。由圖4可知，圖4（b）（e）（j）～（l）中MITSA的初始適應度值均優于其他對比算法，說明佳點集初始化策略為算法尋得了初步更優的可行解；由圖4（a）～（c）可見，MITSA收斂曲線大致呈現冪函數下降，表明MITSA以勻速或勻加速進行迭代搜索，表現出強健的搜索穩定性，且算法的收斂速度較標準TSA增快了2～5倍，其效果緣自于權重因子ω在算法前后期實時監測種群位置更新情況并進行自適應調控，加速了算法收斂效率；各算法在求解多峰函數時，面對復雜的多極值測試函數，依概率小波變異策略對算法的擾動成功率大大提升，特別是在函數f7～f8上的擾動效果非常明顯，使得算法快速收斂到函數理論值附近；圖4（i）～（l）為求解固定函數的平均收斂曲線，各算法均出現了不同程度的停滯現象，而MITSA表現出數次停滯與再搜索的交替情形且最終以最優函數值收斂，其主要得益于MITSA的狀態池存儲了各具特殊狀態的被囊個體信息，多精英協同引導和大范圍的鄰域搜索幫助了被囊群開展最佳可行域的多次探索。綜上，不同算法在各測試函數上的動態尋優進程不同且以MITSA的尋優性能和收斂速度表現最優。

3.4 非參數統計分析

為進一步準確地評估算法改進的有效性，本文采取在顯著水平0.05下進行Wilcoxon秩和檢驗，采用MITSA的每次運行結果與其他算法進行對比，其中N=30，T=500，單多峰測試函數維度選取50d，并進行30次獨立實驗，所得非參數統計結果如表5所示。表中符號“+”表示MITSA相對其他算法具有顯著性，符號“-”表示MITSA相對其他算法無顯著性并用黑體標注，符號“=”、NaN表示MITSA與對比算法性能相當。由表5分析可知，在23個基準測試函數中，大部分P值都遠小于0.05，總體上MITSA的算法性能與其他七種算法在統計上具有顯著性差異。

為更好地對所有算法進行定量分析，本文對基準測試函數的平均絕對誤差（mean absolute error，MAE）［33］對算法進行排序。MEA計算表達式為

MAE=∑Nfi=1mi-oiNf（38）

其中：mi為算法產生的最優結果的平均值；oi為相應基準函數的理論最優值；Nf為基準函數個數。

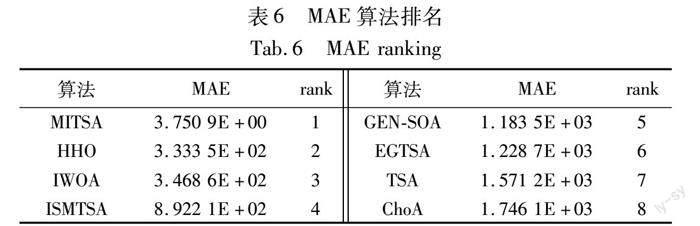
表6給出了這些基準函數的MAE排序。由表6可見，MITSA排名第一，提供了最小的MAE，與其他七種算法相比，進一步驗證了MITSA有效性和穩定性。

3.5 CEC2014測試函數實驗分析

CEC2014 測試函數是由多個基本優化測試函數加權組合而成，具有高復雜性，包括單峰（UN）、多峰（MF）、混合（HF）和復合（CF）類型函數。為進一步驗證MITSA對復雜問題的優化適用性，本文對CEC2014測試集中30個測試函數進行實驗仿真，其中維度d=50，種群規模N=30，取值為［-100，100］，最大迭代次數T=1 000，記錄SOM-KADE、GEN-SOA、TSA、ISMTSA、EGTSA與MITSA獨立運行30次實驗結果的mean值和Std值，限于篇幅，分別選取各類函數的1/3進行展示，其對比統計結果如表7所示，其中黑體數字表示最優值。

由表7分析可知，MITSA整體表現優異，例如在單峰測試函數與多峰測試函數上MITSA幾乎均能夠收斂到理論值附近且表現最佳；在混合測試函數與復合測試函數上MITSA優勢更為明顯，30次獨立實驗持續保持相對更優的指標值，甚至在測試函數CEC25、CEC28、CEC30上，MITSA算法以方差0獲得最優平均值，從而證明了改進算法MITSA相比其他新近元啟發式算法具有更優秀的全局探索能力。

箱線圖主要用于反映數據的分布特征，可以看出數據的對稱性和分散度等信息，適合用于對比分析多組數據的分布情況。為進一步直觀地分析算法的性能表現情況，圖5給出了MITSA與各對比算法在CEC2014測試函數上30次獨立測試最優解的箱線圖對比。

由圖5分析可知，MITSA在測試函數集上的收斂性能均顯著優于其他幾種對比算法：a）箱子中的紅色線條代表中位數，它一般不會受到極大或極小值的影響。其中MITSA的中位數均優于其他算法，表明MITSA具有更好的收斂精度。b）箱體兩頭的虛線代表數據的離散程度，虛線越長數據越分散，虛線越短數據越集中，紅色符號+代表離散數據。圖中MITSA算法30次獨立實驗最優值數據分布比較窄且離散數據少，說明MITSA具有相對較強的多輪測試高精度同步特性和良好算法穩健性。c）箱體上下端分別表示上下四分位數，圖中MITSA的上四分位數仍明顯優于其他算法的下四分位數，說明本文算法對問題解空間的充分探索和開采且以高精度尋得全局最優解。綜上，由表7和圖5的結果對比分析均驗證了MITSA算法對求解不同復雜優化問題的適用性和強勁的競爭力。

4 結束語

為提升標準TSA的全局搜索性能和抗停滯能力，本文提出了一種多策略融合改進的自適應被囊群算法。該算法使用佳點集策略提升了種群的均勻遍歷性，提出多精英協同引導機制優化了標準TSA的全局探索性能，利用自適應權重實時監測種群進化情況，更好地平衡了算法的全局探索與局部開采能力，采取依概率的小波變異策略增強了局部極值逃逸能力并提升收斂速度，四種改進策略分工明確，協同實施，共同提升了被囊群算法的綜合性能，并根據Markov鏈理論證明了 MITSA的全局收斂性。數值實驗結果表明，MITSA的不同改進策略有效性顯著，較各對比算法，MITSA具有更優越的求解精度、魯棒性和顯著性差異，是解決高維復雜優化問題的一種可行且有效的選擇。接下來的工作將進一步拓寬MITSA的應用領域，特別是高維多目標優化、特征選擇、機器博弈等領域。

參考文獻：

［1］Kaur S， Awasthi L K， Sangal A L， et al. Tunicate swarm algorithm： a new bio-inspired based metaheuristic paradigm for global optimization［J］. Engineering Applications of Artificial Intelligence， 2020，90（4）： 103541.

［2］Kennedy J， Eberhart R. Particle swarm optimization［C］//Proc of International Conference on Neural Networks. Piscataway，NJ： IEEE Press， 1995： 1942-1948.

［3］Holland J H. Genetic algorithms［J］. Scientific American， 1992，267（1）： 66-73.

［4］Mirjalili S. SCA： a sine cosine algorithm for solving optimization problems［J］. Knowledge-Based Systems， 2016，96（2）： 120-133.

［5］Mirjalili S， Mirjalili S M， Lewis A. Grey wolf optimizer［J］. Advances in Engineering Software， 2014， 69（3）： 46-61.

［6］Dhiman G， Kumar V. Multi-objective spotted hyena optimizer： a multi-objective optimization algorithm for engineering problems［J］. Knowledge-Based Systems， 2018，150： 175-197.

［7］Dhiman G， Kumar V. Emperor penguin optimizer： a bio-inspired algorithm for engineering problems［J］. Knowledge-Based Systems， 2018，159（1）： 20-50.

［8］李健， 褚超， 郭康樂， 等. 基于TSA與模型匹配的木材缺陷圖像閾值分割［J］. 林業和草原機械， 2020，1（3）： 48-52. （Li Jian， Chu Chao， Guo Kangle， et al. Thresholding segmentation of wood defect image based on TSA and model matching［J］. Forestry and Grassland Machinery， 2020，1（3）： 48-52.）

［9］Abdolinejhad F， Khayati G R， Raiszadeh R， et al. An improved optimization model for predicting Pb recovery efficiency from residual of liberator cells： a hybrid of support vector regression and modified tunicate swarm algorithm［J］. Journal of Material Cycles and Waste Management， 2021，23（5）： 1855-1872.

［10］Sharifi M R， Akbarifard S， Qaderi K， et al. Comparative analysis of some evolutionary-based models in optimization of dam reservoirs ope-ration［J］. Scientific Reports， 2021，11（1）： 15611.

［11］Wang Jianzhou，Wang Shuai，Li Zhiwu. Wind speed deterministic forecasting and probabilistic interval forecasting approach based on deep learning， modified tunicate swarm algorithm， and quantile regression［J］. Renewable Energy， 2021， 179： 1246-1261.

［12］秦維娜， 張達敏， 張琳娜， 等. 異構網絡中基于被囊群算法的D2D通信資源分配［J/OL］. 小型微型計算機系統. （2022-08-11）［2022-12-18］. https：//doi.org/10.20009/j.cnki.21-1106/TP.2022-0089. （Qin Weina， Zhang Damin， Zhang Linna， et al. D2D communication resource segmentation based on tunicate swarm algorithm in heterogeneous networks［J/OL］. Journal of Chinese Computer Systems. （2022-08-11）［2022-12-18］. https：//doi.org/10.20009/j.cnki.21-1106/TP.2022-0089.）

［13］Houssein E H， Helmy B E D， Elngar A A， et al. An improved tunicate swarm algorithm for global optimization and image segmentation［J］. IEEE Access， 2021，9： 56066-56092.

［14］Fetouh T， Elsayed A M. Optimal control and operation of fully automated distribution networks using improved tunicate swarm intelligent algorithm［J］. IEEE Access， 2020， 8： 129689-129708.

［15］Li Lingling， Liu Zhifeng， Tseng M L， et al. Improved tunicate swarm algorithm： solving the dynamic economic emission dispatch problems［J］. Applied Soft Computing， 2021，108（5）： 107504.

［16］屈遲文， 彭小寧. 信息共享的記憶被囊群算法［J］. 模式識別與人工智能， 2021，34（7）： 605-618. （Qu Chiwen， Peng Xiaoning. Tunicate swarm algorithm for information sharing［J］. Pattern Re-cognition and Artificial Intelligence， 2021，34（7）： 605-618.）

［17］史鴻鋒， 李永林. 精英反向黃金正弦被囊群優化算法［J］. 智能計算機與應用， 2021，11（11）： 189-193， 197. （Shi Hongfeng， Li Yonglin. Elite reverse golden sine enveloped group optimization algorithm［J］. Intelligent Computers and Applications， 2021，11（11）： 189-193，197.）

［18］李在友， 孫艷斌， 王曉光， 等. 基于改進被囊群算法的露天礦無人駕駛卡車運輸調度［J］. 工礦自動化， 2022， 48（6）： 87-94，127. （Li Zaiyou， Sun Yanbin， Wang Xiaoguang， et al. Driverless truck transportation scheduling in open-pit mine based on improved encapsulated group algorithm［J］. Industrial and Mine Automation， 2022，48（6）： 87-94，127.）

［19］李志俊， 程家興. 基于數論佳點集的遺傳算法初始種群均勻設計［J］. 電腦與信息技術， 2007，15（4）： 29-32. （Li Zhijun， Cheng Jiaxing. Uniform design of initial population of genetic algorithm based on good point set［J］. Computer and Information Techno-logy， 2007，15（4）： 29-32.

［20］He Guang， Lu Xiaoli. Good point set and double attractors based-QPSO and application in portfolio with transaction fee and financing cost［J］. Expert Systems with Applications， 2022，209（15）： 118339.

［21］馮增喜， 李嘉樂， 葛珣， 等. 融合多策略改進鯨魚優化算法及其應用［J/OL］. 計算機集成制造系統. （2023-01-05）［2023-03-12］. http：//kns.cnki.net/kcms/detail/11.946.tp.20230104.1215.014.html. （Feng Zengxi， Li Jiale， Ge Xun， et al. Integrating multi strategy improved whale optimization algorithm and its application［J/OL］. Computer Integrated Manufacturing System. （2023-01-05）［2023-03-12］. http：//kns.cnki.net/kcms/detail/11.5946.tp.20230104.1215.014.html.）

［22］Khishe M， Mosavi M R. Chimp optimization algorithm［J］. Expert Systems with Applications， 2020， 149： 113338.

［23］Faramarzi A， Heidarinejad M， Stephens B， et al. Equilibrium optimizer： a novel optimization algorithm［J］. Knowledge-Based Systems， 2020，191： 105190.

［24］Arabali A， Khajehzadeh M， Keawsawasvong S， et al. An adaptive tunicate swarm algorithm for optimization of shallow foundation［J］. IEEE Access， 2022，10： 39204-39219.

［25］Ling S H， Iu H H C， Chan K Y， et al. Hybrid particle swarm optimization with wavelet mutation and its industrial applications［J］. IEEE Trans on Systems， Man， and Cybernetics， Part B （Cyberne-tics） ， 2008， 38（3）： 743-763.

［26］胡競杰， 儲昭碧， 郭愉樂， 等. 基于自適應t分布與動態權重的樽海鞘群算法［J］. 計算機應用研究， 2023， 40（7）：2068-2074. （Hu Jingjie， Chu Zhaobi， Guo Yule， et al. Salp swarm algorithm based on adaptive t-distribution and dynamic weight［J］. Application Research of Computers， 2023，40（7）：2068-2074.）

［27］盧夢蝶， 魯海燕， 侯新宇， 等. 融合柯西變異的鳥群與算術混合優化算法［J］. 計算機工程與應用， 2023，59（14）：62-75. （Lu Mengdie， Lu Haiyan， Hou Xinyu， et al. Hybrid algorithm of bird swarm algorithm and arithmetic optimization algorithm based on Cauchy mutation［J］. Computer Engineering and Applications， 2023，59（14）：62-75.）

［28］馮文濤， 鄧兵. 鯨魚優化算法的全局收斂性分析及參數選擇研究［J］. 控制理論與應用， 2021，38（5）： 641-651. （Feng Wentao， Deng Bing. Global convergence analysis and parameter selection of whale optimization algorithm［J］. Control Theory and Applications， 2021，38（5）： 641-651.）

［29］Heidari A A， Mirjalili S， Faris H， et al. Harris hawks optimization： algorithm and applications［J］. Future Generation Computer Systems， 2019， 97： 849-872.

［30］王梓辰， 竇震海， 董軍， 等. 多策略改進的自適應動態鯨魚優化算法［J］. 計算機工程與設計， 2022，43（9）： 2638-2645. （Wang Zichen， Dou Zhenhai， Dong Jun， et al. Multi-strategy improved adaptive dynamic whale optimization algorithm［J］. Computer Engineering and Design， 2022， 43（9）： 2638-2645.）

［31］Liu Xinyu，Li Guangquan，Shao Peng. A multi-mechanism seagull optimization algorithm incorporating generalized opposition-based nonli-near boundary processing［J］. Mathematics， 2022，10（18）： 3295.

［32］閆李， 馬佳慧， 柴旭朝， 等. 基于知識引導的自適應動態多模態差分進化算法［J/OL］. 控制與決策. （2022-07-12）［2022-11-17］. https：//doi.org/10.13195/j.kzyjc.2022.0168. （Yan Li， Ma Jiahui， Chai Xuzhao， et al. Adaptive dynamic multimodal differential evolution algorithm based on knowledge guidance［J/OL］. Control and Decision. （2022-07-12）［2022-11-17］.? https：//doi.org/10.13195/j.kzyjc.2022.0168.）

［33］高晨峰， 陳家清， 石默涵. 融合黃金正弦和曲線自適應的多策略麻雀搜索算法［J］. 計算機應用研究， 2022， 39（2）： 491-499. （Gao Chenfeng， Chen Jiaqing， Shi Mohan. Multi-strategy sparrow search algorithm based on gold sine and curve adaptive［J］. Application Research of Computers， 2022，39（2）： 491-499.

收稿日期：2023-02-10；修回日期：2023-03-27? 基金項目：教育部規劃基金青年項目（21YJCZH204）；遼寧省自然科學基金資助項目（2020-MS-301）；遼寧省教育廳項目（LJKMZ20220694）

作者簡介：柴巖（1970-），女，遼寧阜新人，教授，碩導，碩士，主要研究方向為最優化理論與應用；李廣友（1997-），女（通信作者），四川達州人，碩士，主要研究方向為最優化理論與應用（irenelgy@163.com）；任生（1997-），男，遼寧葫蘆島人，碩士，主要研究方向為最優化理論與應用；許兆楠（1996-），女，內蒙古赤峰人，碩士，主要研究方向為最優化理論與應用．