也談自制簡易密度計的豎直漂浮問題

鄔啟超

(蘇州工業園區星灣學校,江蘇 蘇州 215021)

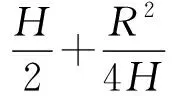
1 密度計的穩定平衡狀態

漂浮在水中的物體有兩個心,重心與浮心,重心是重力的作用點,浮心是浮力的作用點,浮心的位置就是那部分被排開液體重心的位置,[2]對于密度均勻的浮體,當其處在豎直漂浮狀態時會有部分露出水面,故重心一定高于浮心,如圖1所示.密度計屬于非均勻浮體,且質量集中在底部,密度計豎直漂浮時便存在浮心高于重心的情況,[3]當豎直漂浮的密度計受到擾動時,重力與浮力的力偶矩是恢復力矩,如圖2所示,因此平衡態穩定.生活中常見的密度計,上段細且粗細均勻,中下段稍大呈泡狀,底部裝有小鉛粒或水銀(密度大),這樣可以在滿足精確度的前提下盡量地提高浮心并降低重心,從而讓密度計能夠穩定豎直漂浮.

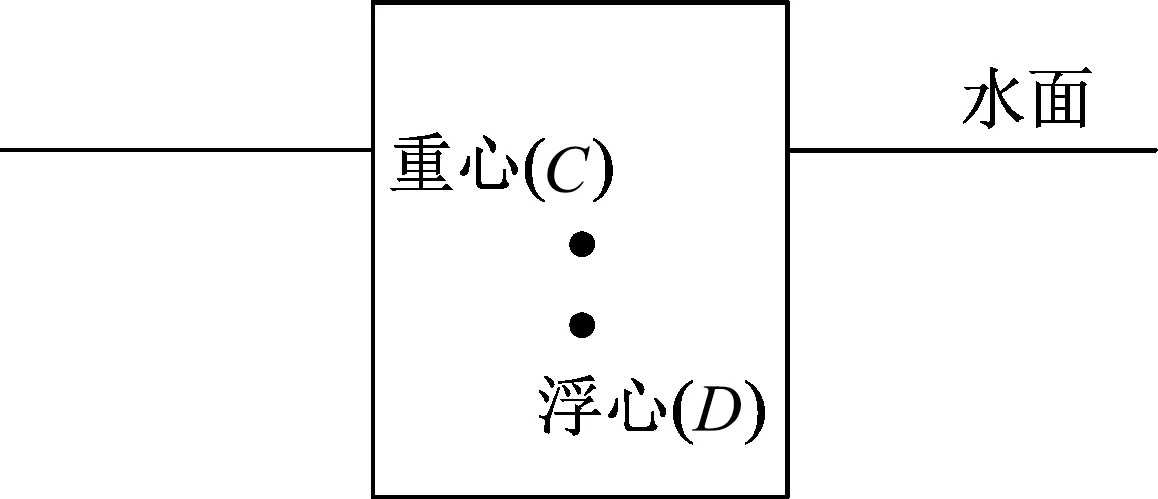
圖1

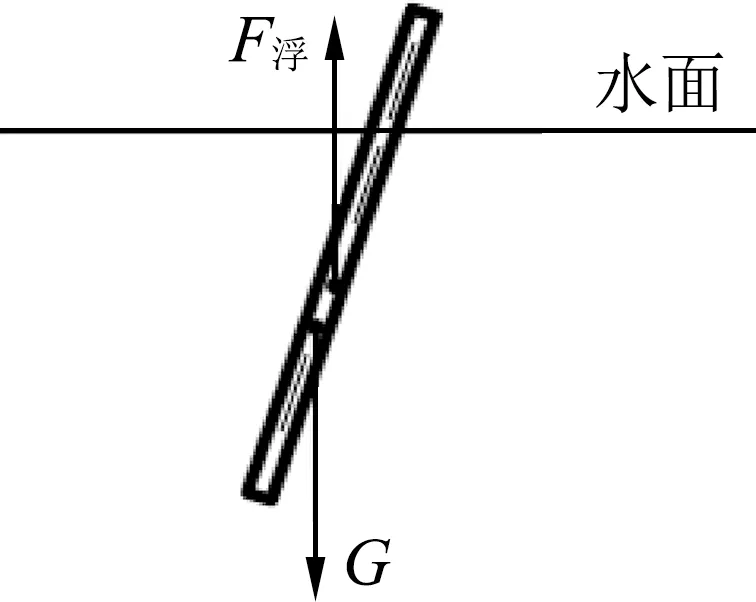
圖2

2 密度計浮心與重心間距與配重的關系

在實際制作簡易密度計時會發現當密度計豎直漂浮后繼續增加配重密度計會更穩定,這是為何呢?我們可以建構如圖3所示的模型進行說明,假設密度計未加配重時的質量為m0,重心(C1)距密度計底部為h1,加入配重(以細沙為例)的重心(C2)距密度計底部為h2,此時密度計的總質量為M,密度計的重心距密度計底部距離可表示為

圖3

(1)

由配重的質量與密度以及密度計的底部半徑可以將h2近似表示成

(2)

將式(2)代入式(1),化簡后得

(3)

若密度計在水中豎直漂浮,根據浮力等于重力易得浮心與密度計底部的距離為

(4)

由于密度計在液體中漂浮時(浮力等于重力),必有浮心與重心在同一鉛直線上,否則無法滿足力矩的平衡.式(4)-式(3)得兩心距離為

(5)

因為浮心高于重心時密度計可以豎直漂浮,可以把浮心等于重心看作是此狀態的極限情況,令式(5)等于0,解得此時密度計的質量為

(6)

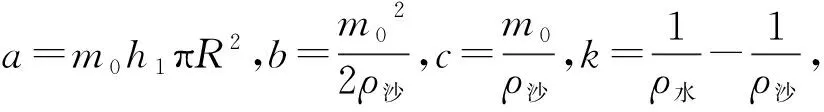
(7)

由式(7)可知,當M≥M1時L隨M增大是單調遞增的,因此在密度計質量達到M1后隨著配重的增加,當密度計受到擾動后恢復力矩將更大,使得豎直漂浮狀態更穩定.

3 浮心低于重心時豎直漂浮狀態的討論

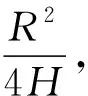
(8)

將式(3)與式(4)代入式(8),使式(8)成立,密度計質量M須滿足

(9)

M2k+2cM-2(a+b)≥0,

(10)

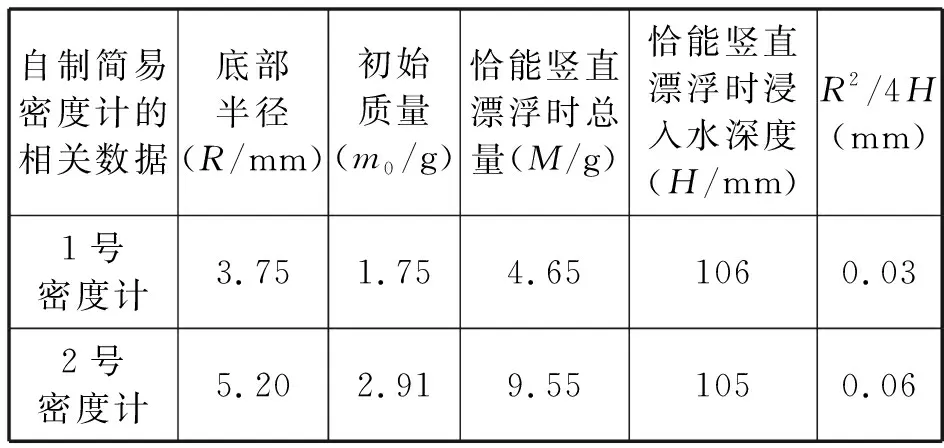
表1

事實上,對于一個漂浮體,其穩定平衡的充分必要條件是重心與浮心的高度差在浮力等于重力這一限定下取極小值.[3]在實際制作簡易密度計時,隨著配重的增加密度計靜止時的狀態逐漸趨于豎直方向,可見,隨著配重質量的變化密度計會通過調整傾斜角度來實現極小值的滿足,而極小值趨近于0.