基于新評價指標自適應預測的動態多目標優化算法

李二超，張生輝

基于新評價指標自適應預測的動態多目標優化算法

李二超*，張生輝

（蘭州理工大學 電氣工程與信息工程學院，蘭州 730050）（ ? 通信作者電子郵箱lecstarr@163.com）

現實生活中的多目標優化問題（MOP）大多為動態多目標優化問題（DMOP），此類問題的目標函數、約束條件和決策變量都可能隨時間的變化而發生改變，這需要算法在環境變化后快速適應新的環境，且在保證Pareto解集多樣性的同時快速收斂到新的Pareto前沿。針對此問題，提出一種基于新評價指標自適應預測的動態多目標優化算法（NEI-APDMOA）。首先，在種群非支配排序過程中提出一種優于擁擠度的新評價指標，并分階段平衡收斂快速性和種群多樣性，使種群的收斂過程更加合理；其次，提出一種可判斷環境變化強弱的因子，為預測階段提供有價值信息，并引導種群更好地適應環境變化；最后，根據環境變化因子匹配3種更加合理的預測策略，使種群快速響應環境變化。將NEI-APDMOA與DNSGA-Ⅱ-A（Dynamic Non-dominated Sorting Genetic Algorithm-Ⅱ-A）、DNSGA-Ⅱ-B（Dynamic Non-dominated Sorting Genetic Algorithm-Ⅱ-B）和PPS（Population Prediction Strategy）算法在9個標準動態測試函數上進行對比。實驗結果表明，NEI-APDMOA分別在9、4和8個測試函數上取得了最優的平均反世代距離（IGD）值、平均間距（SP）值和平均世代距離（GD）值，可以更快地響應環境變化。

動態多目標優化；進化算法；評價指標；非支配排序；預測策略

0 引言

很多問題都可以抽象化為具有多個相互沖突目標的多目標優化問題（Multi-objective Optimization Problem，MOP）［1］，現實生活中多目標優化問題本質上是動態的，動態多目標優化問題（Dynamic Multi-objective Optimization Problem， DMOP）［2］的目標函數、約束條件和決策變量都會隨時間（環境）動態變化，它的最優解集也會隨時間（環境）而動態變化。解決DMOP要求算法在環境變化后最大限度地跟蹤近似Pareto最優解集（Pareto optimal Solution set， PS）和Pareto前沿（Pareto optimal Front， PF），而不是僅求解單一的最優值或 Pareto最優解。因此，動態多目標優化算法需要在傳統靜態多目標算法上作出調整和改進。

近年來，在提高自主進化能力從而更好地尋找最優解和解決動態優化問題中種群快速適應環境能力方面，研究者們提出了許多適應DMOP的動態多目標優化算法［3-7］，一些學者將記憶策略和預測策略引入動態多目標優化算法解決此類問題。記憶策略利用先前搜索的最優解加快收斂進程，提高收斂速度。Sahmoud等［8］提出一種包含搜索種群和主種群的算法，搜索種群隨環境變化重新初始化，并更新非支配記憶池，在記憶池和主種群中選擇初始種群。Jiang等［9］結合記憶策略和流形遷移學習方法，提出基于流形的動態多目標優化算法，根據歷史信息建立流形空間的遷移模型，生成新環境下的初始種群。預測策略在每次環境變化后指導種群進化，為種群進化提供引導方向，預測種群快速響應新變化。Cao等［10］提出了一種基于支持向量回歸（Support Vector Regression， SVR）的方法生成新環境的初始種群，每個子問題都可以在不同的環境中獲得它相應的解，以形成時間序列。Rong等［11］根據問題特性變化類型提出一種多模型預測方法，對平移、旋轉和復合三類問題變化針對性響應。Wang等［12］提出一種灰色預測模型預測新環境下初始種群，有效提高了種群收斂性，但算法過于依賴預測模型和數據。基于機器學習策略對新環境下種群初始化，與融合多種變化響應的混合策略發揮協同效應，為解決動態多目標問題提供新的思路。Zhao等［13］提出一種新的知識學習策略，通過學習先前搜索經驗提高收斂速度。Gong等［14］提出基于區間相似度的動態多目標進化框架，結合隨機突變策略、決策變量分解策略和環境變化強度預測策略，有效提高算法跟蹤新環境的PF。Feng等［15］通過結合深度學習的自動編碼技術和預測策略重新初始化新種群。Zhang等［16］選取使用線性預測策略、收縮策略和抽樣策略生成種群的非支配個體作為新環境下的初始種群，有效提高算法收斂速度。

此外，檢測環境變化和變化程度是動態多目標優化算法設計中重要環節之一。許多有效算法環境檢測機制十分簡單，大多都采用重新評價個體的方式判斷環境是否發生改變，并通過嵌套合理的數學模型設計動態響應機制。Sahmoud等［17］提出了一系列新的變化檢測機制，一種是檢測種群個體是否發生變化，另一種則是在搜索空間中產生一些新個體檢測環境是否發生變化。Richter［18］提出通過判斷當前代目標解集和新一代目標解集是否具有不同分布的方法，以判斷環境是否發生變化。Jiang等［19］提出一種穩態檢測方法，將所有個體隨機排列后重評估，通過重評估差異證明環境變化與否。

以上方法保持了種群的分布性，對新環境下的種群具有良好的跟蹤環境能力；然而，在種群收斂時不能保持很好的收斂速度，并且在解決環境變化時具有一定的盲目性，不能為新環境下種群提供正確引導。因此，提高種群自主進化能力并在環境發生變化后快速跟蹤環境，幫助算法對新變化作出快速響應成為提高算法收斂速度和收斂性的研究重點。

基于上述問題，綜合考慮算法跟蹤環境變化能力、收斂快速性等問題，提出一種基于新評價指標的自適應預測動態多目標優化算法（Adaptive Prediction Dynamic Multi-objective Optimization Algorithm based on New Evaluation Index， NEI-APDMOA）。與現有其他算法相比，該算法具有以下特點：

1）引入一種新的非支配排序指標，平衡種群多樣性和收斂快速性，解決解集分布不均等問題，有效提高種群自主進化能力，加快算法收斂。

2）提出一種判斷動態環境變化強弱的算子，判斷環境變化前后線性相關性，為算法跟蹤環境變化提供依據。

3）設計自適應響應機制，根據環境變化強弱選擇相應的響應機制生成新環境下預測種群，提高環境變化跟蹤能力。

本文采用5個FDA系列［20］、2個DMOP系列［21］和2個DTLZ系列［22］涵蓋3類動態多目標問題的標準測試集，將本文算法與DNSGA-Ⅱ-A（Dynamic Non-dominated Sorting Genetic Algorithm-Ⅱ-A）［6］、DNSGA-Ⅱ-B（Dynamic Non-dominated Sorting Genetic Algorithm-Ⅱ-B）［6］、PPS（Population Prediction Strategy）算法［23］對比。實驗結果表明，NEI-APDMOA能更好地平衡種群進化時多樣性和收斂性，保持更快的收斂速度，具有更好的動態環境跟蹤能力，更加合理地響應環境變化。

1 問題描述

DMOP是以最小化多目標優化問題為研究對象，數學定義一個具有維決策變量、個目標函數的DMOP可以描述為：

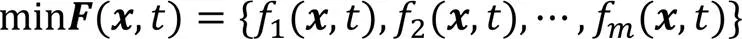
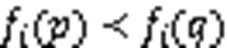
隨著環境的變化，根據PS和PF的變化情況［24］，動態多目標優化問題可分為以下4類：

第1類問題 PS隨時間變化，PF不隨時間變化。

第2類問題 PS不隨時間變化，PF隨時間變化。

第3類問題 PS和PF都隨時間變化。

第4類問題 PS和PF都不隨時間變化。

2 相關工作

2.1　動態多目標優化算法框架

目前動態多目標優化算法大多都是基于靜態多目標優化算法基礎上改進，當環境沒有發生改變時，將動態多目標優化問題以時間維度分割成多個靜態多目標優化問題，并優化求解。在靜態算法基礎上增加環境變化檢測機制和響應機制，實時檢測當前時刻問題與上一時刻問題的數學模型映射關系。環境變化響應機制是設計動態多目標優化算法的關鍵，當檢測到環境發生改變時，變化響應機制直接影響環境變化后種群的優劣，好的響應機制可以保證種群在新環境下的多樣性和收斂的快速性。

動態多目標優化算法主要框架由3部分組成：靜態多目標優化算法、環境變化檢測機制和環境變化響應機制，算法的主框架流程如圖1所示。

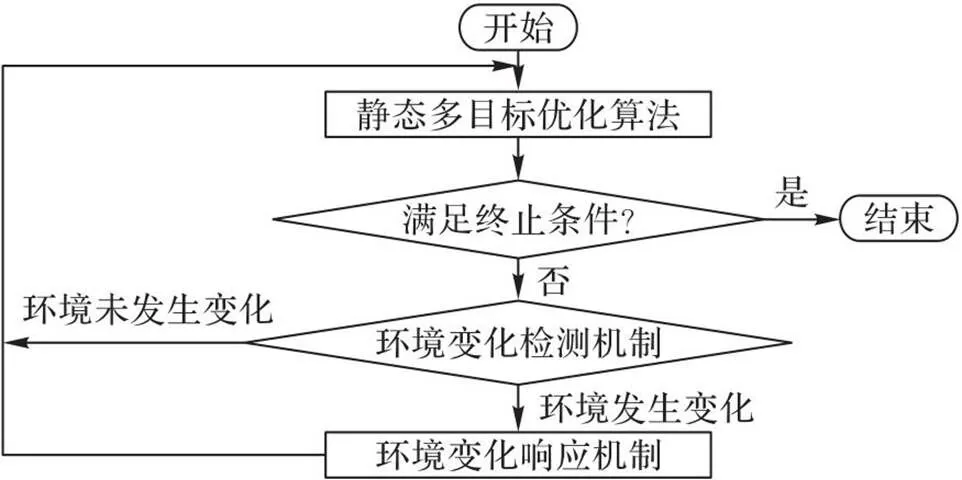
圖1　動態多目標優化算法流程

2.2　熵權TOPSIS評分

TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution）理論模型［25］是一種多目標決策算法，基本原理是通過計算評價樣本與正理想解和負理想解的距離排序，正理想解和負理想解分別是各評價指標中的最優值和最劣值，該數學模型通過對理想解的逼近實現多指標成分綜合分析，如圖2所示。

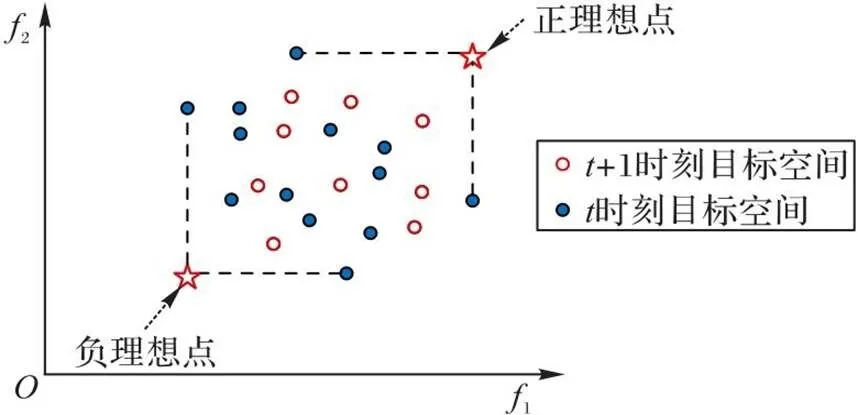
圖2　正理想點和負理想點

熵權法根據各指標信息含量賦予權重系數，更準確地進行目標綜合評價。對采集的原始數據建立評估矩陣如下：

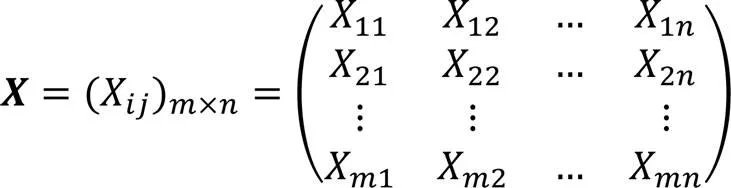
在進行數據處理的過程中，為使原始狀態矩陣中的數據具有可行性，需對原始評估矩陣的評估數據進行正向化和逆向化處理。如果數據中有逆向指標，此時需要使用從數據處理到生成變量的“逆向化”功能處理，讓數據變成正向指標。針對數據越大越優型指標和數據越小越優型指標分別進行正向化（式（3））和逆向化（式（4））處理：

將處理后的正向指標進行標準、歸一化處理，將所有數據歸至0到1之間，解決數據量綱化問題，最終得到矩陣：

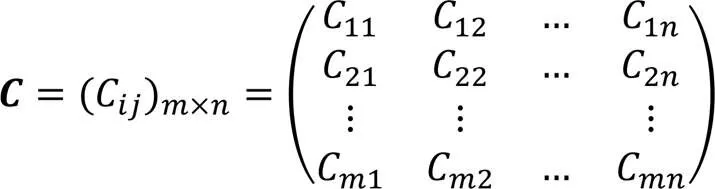
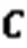
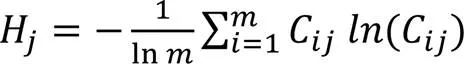
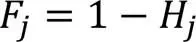
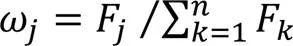
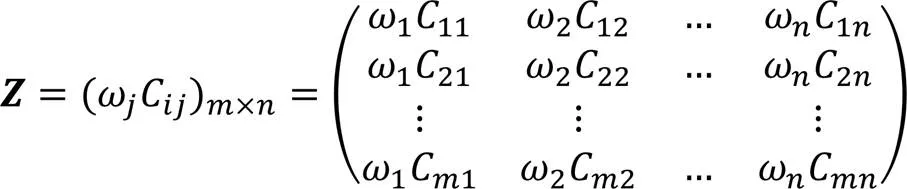
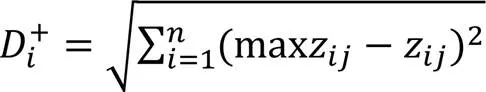
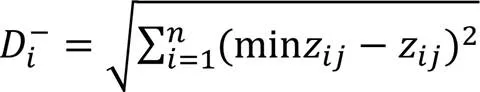
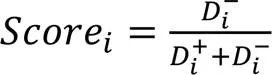
3 NEI?APDMOA

3.1　非支配排序度量指標

多目標優化算法的目的就是協調各個目標函數之間的關系，找出使得各個目標函數都盡可能達到較大（或者較小）的函數值的最優解集。Deb等［6］提出了非支配排序遺傳算法（Non-dominated Sorting Genetic Algorithm-Ⅱ， NSGA-Ⅱ），該算法引入擁擠度和擁擠度比較算子，將擁擠度作為種群個體之間的比較準則，使得準Pareto域中的種群個體均勻擴展到整個Pareto域，保證種群的多樣性。NSGA-Ⅱ簡單有效，已成為多目標優化問題中的基本算法之一。然而，在種群進行快速非支配排序時，只考慮擁擠度不能很好地平衡多目標算法下種群的多樣性和收斂性；在高維目標選擇中，擁擠度不能作為唯一的非支配排序指標，否則將導致解在非支配層上分布不均勻，使算法陷入局部最優。

為使算法在尋優過程中同時兼顧種群多樣性和收斂快速性，本文引入新的非支配排序度量指標，根據種群進化過程動態調整算法的全局搜索和局部開發能力，提高多目標算法收斂性的同時，也提高算法優化效率和非支配解集的質量。

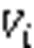
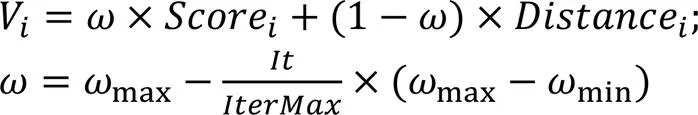
算法1 新度量指標排序法。

輸入 前一時刻的非支配種群；

輸出 更新的種群new。

計算前一時刻非支配種群各指標熵值，得到指標權重矩陣

將前一時刻的非支配種群與指標權重結合，得到加權標準化矩陣

初始化正、負理想解后計算出種群的正、負理想解集

計算種群的熵權TOPSIS評分

返回更新的種群new

3.2　環境檢測機制

一個優秀的環境檢測機制不僅需要判斷環境變化的劇烈程度，即決策空間到目標空間映射發生變化的劇烈程度，還需要判斷環境變化的規律，將當下環境變化規律與響應機制相契合，為響應機制提供更合理、有效的指導。

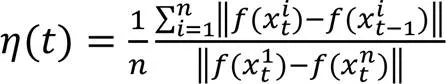
算法針對性選擇部分代表性解，并利用這些解檢測環境是否發生改變，若發生改變，則利用這些解判斷環境變化關聯程度。假設環境在t時刻到t+1時刻發生改變，通過DNSGA-Ⅱ算法在t時刻所選擇個體集合的目標函數所處目標空間位置為實心點，t+1時刻此集合的目標函數所處目標空間位置為空心點，同一解集在不同時刻下的關聯程度如圖3所示。

圖4　參考直線示意圖

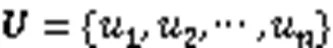
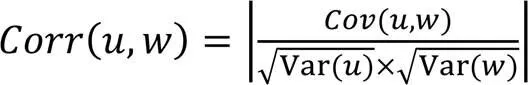
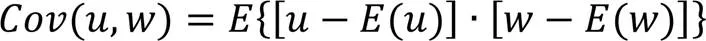
算法2 環境變化檢測機制。

利用環境參考直線公式計算種群、+1的截距矩陣、

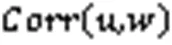
3.3　環境響應機制

3.3.1隨機初始化

當環境發生劇烈變化時，種群在新環境中的移動和進化方向存在很大差異，繼續沿用之前環境的響應機制會使種群不能及時適應新環境的特點，不能快速追蹤環境變化。對新環境支配種群隨機初始化可以保證種群有良好的多樣性，避免陷入局部最優，保證新環境下種群的收斂性。本文算法對種群中一定數量的支配種群個體隨機初始化，非支配種群個體保留上一時刻狀態，在新環境變化后作出響應，保證種群多樣性和新環境下收斂速度。

算法3 隨機初始化策略。

輸入 當前時刻種群，種群大小；

輸出 隨機初始化預測種群random。

選擇/10數量的最優個體best

隨機生成9×/10數量的個體random

合并best與random種群個體組成預測種群random

返回預測種群random

圖5　支配種群個體的隨機初始化

3.3.2質心移動軌跡預測

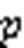
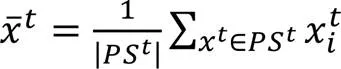
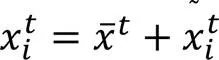
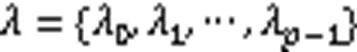
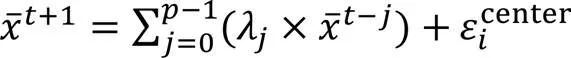
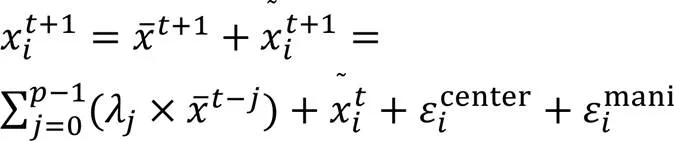
圖6　不同時刻種群輪廓質心

算法4 質心軌跡移動策略。

輸入 當前時刻種群，歷史質心存檔history，歷史輪廓存檔history；

輸出 質心軌跡移動預測種群move。

計算當前種群的質心和輪廓，更新歷史質心存檔history與歷史輪廓存檔history

計算預測種群質心

計算預測種群輪廓

生成并返回質心移動預測種群move

3.3.3慣性隨機預測

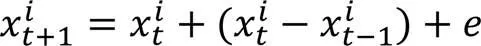
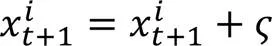
算法5 慣性隨機預測。

輸入 當前種群，前一時刻種群-1，種群大小；

輸出 慣性隨機預測種群inertia。

計算環境變化前后種群時間序列

根據式（23）計算生成當前種群預測點p

預測點鄰域通過高斯擾動產生新預測點集new

合并預測點p和新預測點集new組成預測點集predict

預測點集predict中選擇個的預測種群inertia

返回慣性隨機預測種群inertia

3.4　NEI-APDMOA詳細描述

NEI-APDMOA旨在檢測到環境變化時，實時追蹤環境變化強弱，以算法最快速度響應環境變化，平衡種群分布性和收斂性，使種群更好地適應新環境。NEI-APDMOA的詳細描述如算法6所示。

算法6 NEI-APDMOA。

初始化 種群大小，隨機產生規模為的初始種群，進化代數，進化總代數，交叉概率c，變異概率m

for=1 todo

環境變化不存在線性關系，啟用算法3

生成預測種群；

環境變化存在弱相關關系，啟用算法4

生成預測種群；

環境變化存在強線性關系，啟用算法5

生成預測種群；

end if

輸出預測種群并作為當前初始種群

end if

種群以交叉概率c，變異概率m交叉變異生成子代種群G

for=1 todo

啟用算法1計算子代個體新評價指標V

end for

end for

3.5　計算復雜度分析

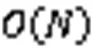
4 測試問題及評價指標

4.1　測試問題

為了驗證本文算法的有效性，選取FDA1～FDA5［20］、DMOP1、DMOP2［21］、DTLZ1和DTLZ2［22］涵蓋3類動態多目標問題的標準測試集進行仿真實驗。其中：FDA1和FDA4屬于第1類問題（真實PS位置隨時間變化，真實PF位置不隨時間變化）；DMOP1屬于第2類問題（真實PS位置不隨時間變化，真實PF位置隨時間變化）；FDA2、FDA3、FDA5和DMOP2屬于第3類問題（真實PS位置和PF位置都隨時間變化）；DTLZ1和DTLZ2的Pareto前沿面都是高維曲面。

4.2　性能指標

為了能夠全面地評價算法的性能表現，本文采用3種廣泛使用的評價指標。

1）反世代距離（Inverted Generational Distance， IGD）［23］。

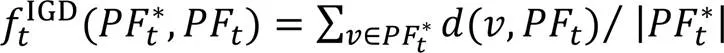
2）世代距離（Generational Distance， GD）［23］。

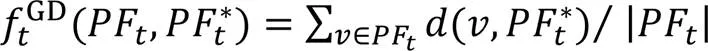
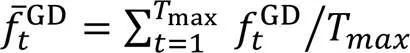
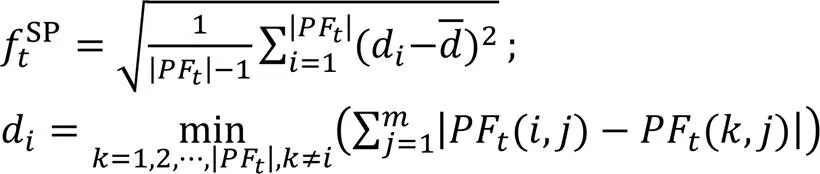
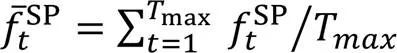
5 實驗與結果分析

5.1　參數設置

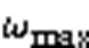
表1　不同度量權重時的平均IGD、SP值

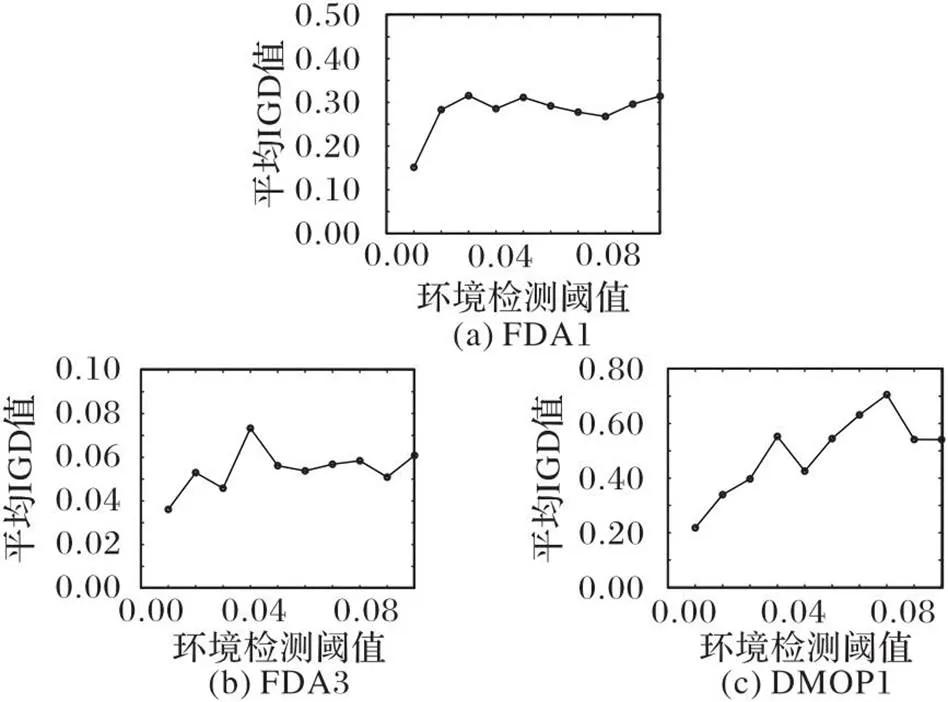
圖7　平均IGD值隨環境檢測閾值的變化曲線

5.2　實驗結果與分析

根據測試函數問題的PS和PF的變化情況進行分類并將本文算法（NEI-APDMOA）與NSGA-Ⅱ-A［6］、NSGA-Ⅱ-B［6］和PPS算法［23］進行對比，在仿真實驗后分別計算各算法在測試函數上的平均IGD、平均SP和平均GD這3種評價指標值，對比情況如表2～4所示，其中：性能“+”“-”和“～”分別表示根據顯著性水平為0.05的Wilcoxon秩和檢驗結果，對應算法得到的指標值結果比NEI-APDMOA較好、較差和相似，各表中最后一行標出了NEI-APDMOA與其他算法對比結果的統計數據。

平均IGD評價標準結果如表2所示，NEI-APDMOA較其余3種對比算法有較大優勢。相較于DNSGA-Ⅱ-A，本文算法有6個測試函數的平均IGD數據表現出色，有3個測試函數結果相似；相較于DNSGA-Ⅱ-B，有7個測試函數NEI-APDMOA表現出色，有2個測試函數結果相似；相較于PPS算法，NEI-APDMOA在全部測試函數中的表現都要出色。通過對比可知，NEI-APDMOA比3種對比算法有更優性能，這主要歸功于引入新評價指標分階段平衡收斂速度和種群多樣性，其次有針對性的環境響應策略也有一定性能提升貢獻。

平均SP評價標準結果如表3所示，相較于DNSGA-Ⅱ-A，NEI-APDMOA有2個測試函數的平均SP數據表現出色，有4個測試函數結果相似，有3個測試函數結果不如DNSGA-Ⅱ-A；相較于DNSGA-Ⅱ-B，NEI-APDMOA有2個測試函數表現出色，有5個測試函數結果相似，另有2個測試函數較差；相較于PPS算法，NEI-APDMOA有2個測試函數表現出色，有3個測試函數結果相似，有4個測試函數表現不如PPS算法。通過對比綜合分析，NEI-APDMOA在新環境下的對新初始種群的預測是導致在部分測試函數上性能略差的主要原因，但NEI-APDMOA整體的收斂性都優于其他3種算法，能夠適應環境變化并快速追蹤Pareto前沿面。

平均GD評價標準比較結果如表4所示。相較于DNSGA-Ⅱ-A，NEI-APDMOA有7個測試函數的平均GD數據表現出色，有1個測試函數結果相似，1個不如比較算法；相較于DNSGA-Ⅱ-B，有7個測試函數NEI-APDMOA表現出色，有1個測試函數結果相似，另有1個測試函數較差；相較于PPS算法，NEI-APDMOA有7個測試函數表現出色，有2個測試函數結果相似。

通過對比可知，NEI-APDMOA分別在9、4、8個測試函數上取得了最優的平均IGD值、平均SP值和平均GD值，相較于對比算法有更好的動態多目標優化性能。

為了直觀展示各算法在不同環境中的綜合性能，跟蹤每個算法在不同類型測試問題上的IGD值演變曲線如圖8所示，具體分析對比如下。

1）動態測試函數FDA1作為第1類問題代表，PS隨時間變化，PF不隨時間變化。在動態測試問題FDA1中，NEI-APDMOA在一開始就具有良好的收斂性，且全局收斂效果明顯優于其他對比算法，說明本文算法獲得的解集更加接近真實的Pareto前沿。但是種群在環境變化前后波動較大，經分析是由于算法在自適應預測機制中生成的預測種群為保持多樣性所導致，算法經過幾代進化后立即收斂，展現出算法能更好適應新環境的能力。NEI-APDMOA可以更快速地適應第1類問題環境的變化，提高了算法在環境變化后的尋優能力，更快速地收斂至理想Pareto前沿。

2）動態測試函數DMOP1作為第2類問題代表，PS不隨時間發生改變，PF隨時間發生改變，DMOP1最優PF呈現凸顯至凹型的變化。NEI-APDMOA在大多數代數中顯示出比其他比較算法更低IGD值，表明NEI-APDMOA產生的解集更加接近真實Pareto前沿，NEI-APDMOA在前沿變化的情況下仍然具有最好的追蹤能力。分析可得，NEI-APDMOA更加適應新環境并快速地收斂至理想Pareto前沿，相較于其他3種算法可以更好地適用于第2類問題。

3）動態測試函數FDA3和DMOP2屬于第3類問題，PS和PF都隨時間變化。對于此類問題，NEI-APDMOA在大部分時間IGD值較小且曲線平穩，說明本文算法有效平衡了收斂速度和種群多樣性，環境變化后響應速度更快，算法更加穩定。得益于NEI-APDMOA根據環境變化強弱選擇相應的響應機制，有效降低環境變化后的種群波動，通過有效判斷環境變化因子，為選擇合理的響應機制提供有效信息。綜合對比分析可知，NEI-APDMOA可以更快更準確地響應此類型的環境變化，表現出較為穩定的收斂性和分布性，相較于其余3種算法更加適用于PF和PS都隨時間變化的第3類問題。

4）動態測試函數DTLZ1和DTLZ2作為高維問題代表，Pareto前沿面都是高維的。對于此類問題，NEI-APDMOA在環境變化初始階段收斂性優于其余3種算法，可以以較快速度收斂至理想解集，經過進化收斂性與其他算法相差不大。對比分析可知，NEI-APDMOA通過使用提出的新指標更加合理地進行非支配排序，更好地解決高維動態多目標問題。

為更好地展現NEI-APDMOA在不同時刻產生的Pareto解在Pareto前沿上的分布，圖9～10給出DMOP1和DTLZ2不同類型測試函數的前沿分布情況。其中，DMOP1測試函數繪出同一環境下不同進化階段的前沿分布情況，DTLZ2測試函數繪出不同環境下的前沿分布情況。

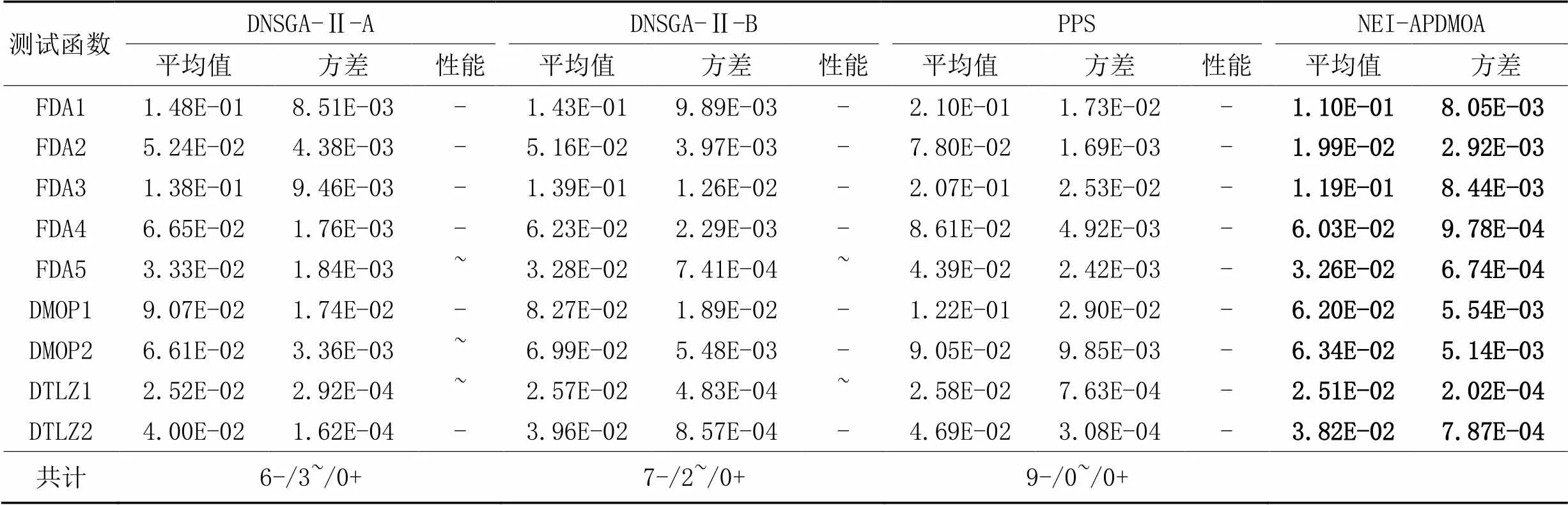
表2　四種算法的平均IGD值統計

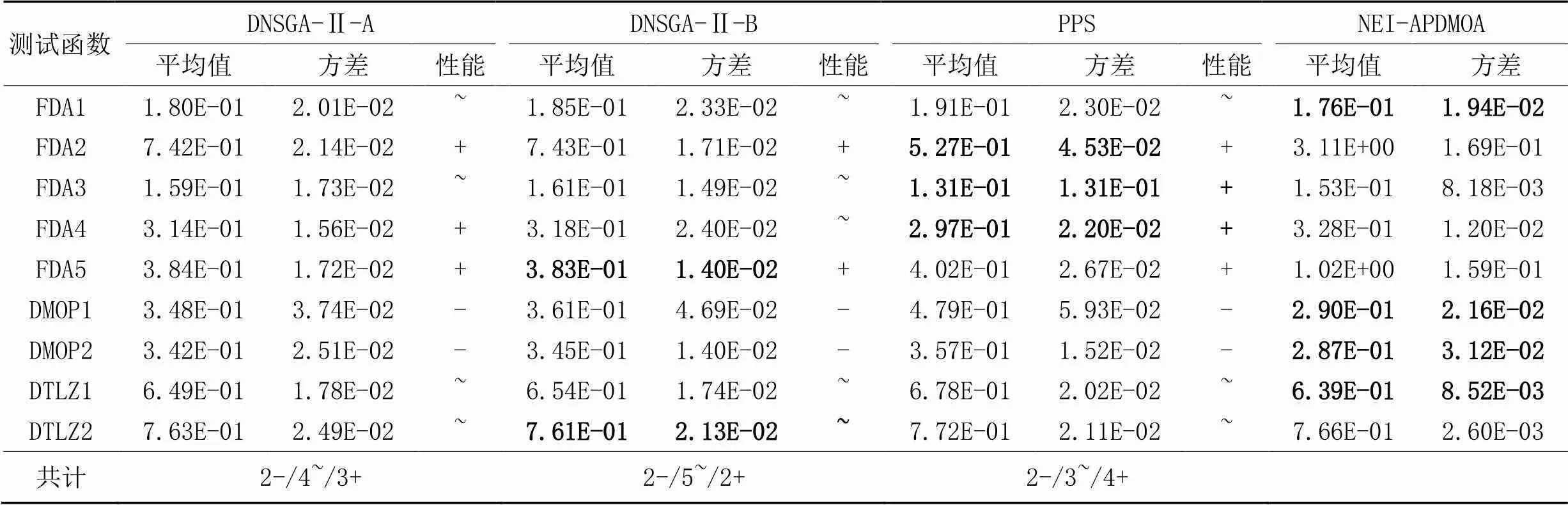
表3　四種算法的平均SP值統計

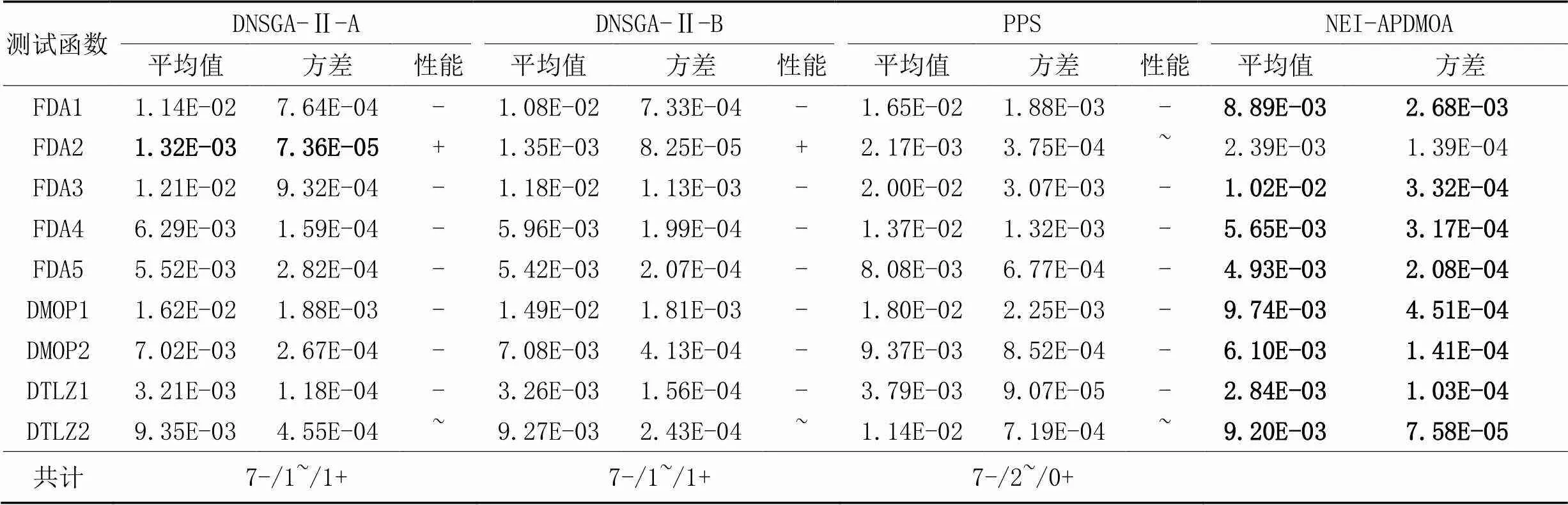
表4　四種算法的平均GD值統計

如圖9所示，在同一環境進化初期選擇最優個體時，NEI-APDMOA由于引入新評價指標，選擇全局性最優個體權重較大，側重于全局搜索，較DNSGA-Ⅱ-A有更快收斂速度；當進化處于后期時，隨著選擇全局性最優個體權重下降，算法從初期側重于全局尋優變為側重于局部尋優，增加種群多樣性，所得Pareto解增多，分布較DNSGA-Ⅱ-A均勻，更加接近測試函數理想Pareto前沿。

DTLZ2問題如圖10所示，NEI-APDMOA在第1次環境變化時較PPS算法有較快的收斂速度；由于本文算法根據環境變化類型選擇響應機制，當第5次環境變化時，大部分個體收斂趨勢較好，但種群分布性依然欠佳；隨著種群進化，在第9次環境變化時，種群的分布性得到改善，NEI-APDMOA較對比算法PPS更加快速適應新環境。

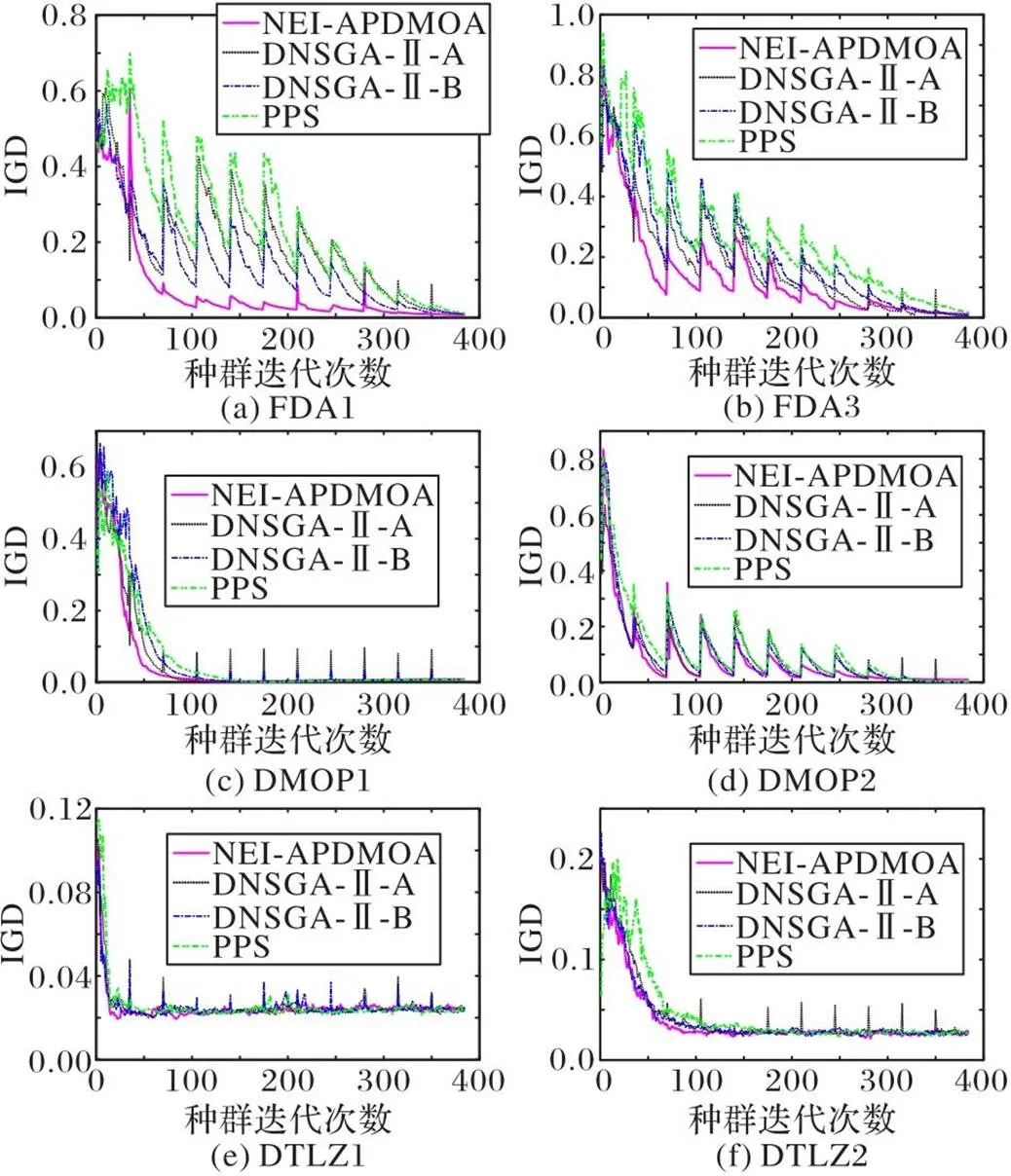
圖8　不同算法在6個測試函數上的IGD值演變曲線

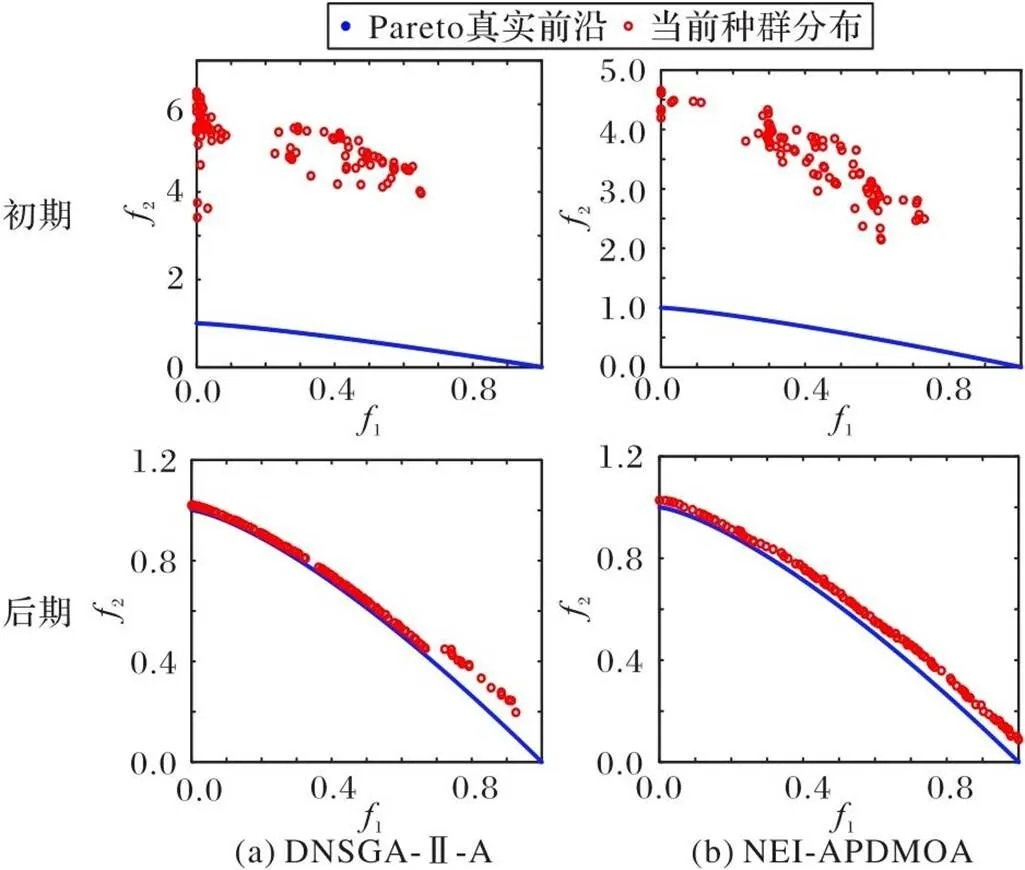
圖9　DMOP1在同一環境下不同階段的解集分布

通過對比4個算法在不同動態類型測試函數上的平均IGD、平均SP和平均GD這3種評價指標，并分析4個算法的平均IGD值演變曲線和不同環境變化種群前沿分布可知，NEI-APDMOA可以很好地處理不同類型和維度的動態問題，在環境變化中加快收斂速度的同時兼顧種群的多樣性和分布性，更好地適用于解決不同類型的動態優化問題。

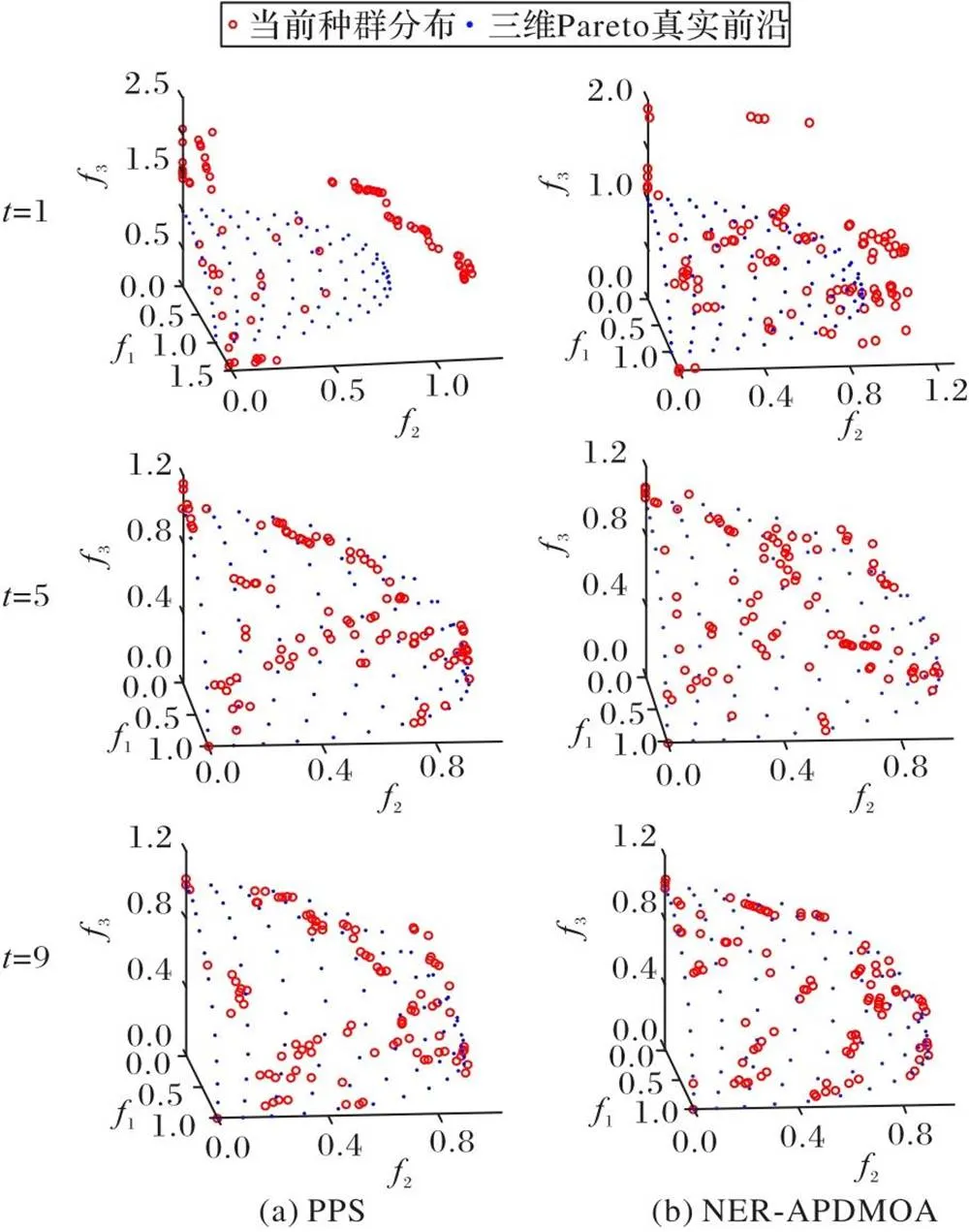
圖10　DTLZ2在不同環境下的解集分布

6 結語

設計動態多目標進化算法的核心問題就是當環境發生變化時，及時追蹤變化的PF或PS并保持良好的分布性，本文提出一種基于新評價指標的自適應預測動態多目標優化算法（NEI-APDMOA）。NEI-APDMOA在5個FDA系列、2個DMOP系列和2個DTLZ系列涵蓋3類動態多目標問題的標準測試集上，與3個現有算法作仿真對比。實驗結果表明，NEI-APDMOA在進化過程中平衡種群多樣性和收斂性，以較快速度獲得更好的收斂性和分布性解集，快速適應環境變化的同時有效避免陷入局部最優，在處理不同類型和維度的動態優化問題上優勢明顯。此外，當遇到部分復雜環境時，算法雖同樣可以較好預測新環境下種群，但也會出現較少數的個體偏離現象影響算法性能，故如何有效判斷新環境下預測種群是否可靠，設計一種更加合理的自適應預測機制將是未來研究的重點。

[1] ZHOU A， QU B Y， LI H， et al. Multiobjective evolutionary algorithms： a survey of the state of the art［J］. Swarm and Evolutionary Computation， 2011， 1（1）：32-49.

[2] 劉若辰，李建霞，劉靜，等. 動態多目標優化研究綜述［J］. 計算機學報， 2020， 43（7）：1246-1278.（LIU R C， LI J X， LIU J， et al. A survey on dynamic multi-objective optimization［J］. Chinese Journal of Computers， 2020， 43（7）：1246-1278.）

[3] RUAN G， YU G， ZHENG J， et al. The effect of diversity maintenance on prediction in dynamic multi-objective optimization［J］. Applied Soft Computing， 2017， 58： 631-647.

[4] MURUGANANTHAM A， TAN K C， VADAKKEPAT P. Evolutionary dynamic multiobjective optimization via Kalman filter prediction［J］. IEEE Transactions on Cybernetics， 2016， 46（12）： 2862-2873.

[5] DEB K， RAO N U B， KARTHIK S. Dynamic multi-objective optimization and decision-making using modified NSGA-Ⅱ： a case study on hydro-thermal power scheduling［C］// Proceedings of the 2007 International Conference on Evolutionary Multi-Criterion Optimization， LNCS 4403. Berlin： Springer， 2007： 803-817.

[6] DEB K， PRATAP A， AGARWAL S， et al. A fast and elitist multiobjective genetic algorithm： NSGA-Ⅱ［J］. IEEE Transactions on Evolutionary Computation， 2002， 6（2）： 182-197.

[7] AZEVEDO C R B， ARAúJO A F R. Generalized immigration schemes for dynamic evolutionary multiobjective optimization［C］// Proceedings of the 2011 IEEE Congress of Evolutionary Computation. Piscataway： IEEE， 2011： 2033-2040.

[8] SAHMOUD S， TOPCUOGLU H R. A memory-based NSGA-Ⅱ algorithm for dynamic multi-objective optimization problems［C］// Proceedings of the 2016 European Conference on the Applications of Evolutionary Computation， LNCS 9598. Cham： Springer， 2016： 296-310.

[9] JIANG M， WANG Z， QIU L， et al. A fast dynamic evolutionary multiobjective algorithm via manifold transfer learning［J］. IEEE Transactions on Cybernetics， 2021， 51（7）： 3417-3428.

[10] CAO L， XU L， GOODMAN E D， et al. Evolutionary dynamic multiobjective optimization assisted by a support vector regression predictor［J］. IEEE Transactions on Evolutionary Computation， 2020， 24（2）： 305-319.

[11] RONG M， GONG D， PEDRYCZ W， et al. A multimodel prediction method for dynamic multiobjective evolutionary optimization［J］. IEEE Transactions on Evolutionary Computation， 2020， 24（2）： 290-304.

[12] WANG C， YEN G G， JIANG M. A grey prediction-based evolutionary algorithm for dynamic multiobjective optimization［J］. Swarm and Evolutionary Computation， 2020， 56： No.100695.

[13] ZHAO Q， YAN B， SHI Y， et al. Evolutionary dynamic multiobjective optimization via learning from historical search process［J］. IEEE Transactions on Cybernetics， 2022， 52（7）： 6119-6130.

[14] GONG D， XU B， ZHANG Y， et al. A similarity-based cooperative co-evolutionary algorithm for dynamic interval multiobjective optimization problems［J］. IEEE Transactions on Evolutionary Computation， 2020， 24（1）： 142-156.

[15] FENG L， ZHOU W， LIU W， et al. Solving dynamic multiobjective problem via autoencoding evolutionary search［J］. IEEE Transactions on Cybernetics， 2022， 52（5）： 2649-2662.

[16] ZHANG Q， YANG S， JIANG S， et al. Novel prediction strategies for dynamic multiobjective optimization［J］. IEEE Transactions on Evolutionary Computation， 2020， 24（2）： 260-274.

[17] SAHMOUD S， TOPCUOGLU H R. Sensor-based change detection schemes for dynamic multi-objective optimization problems［C］// Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence. Piscataway： IEEE， 2016： 1-8.

[18] RICHTER H. Detecting change in dynamic fitness landscapes［C］// Proceedings of the 2009 IEEE Congress on Evolutionary Computation. Piscataway： IEEE， 2009： 1613-1620.

[19] JIANG S， YANG S. A steady-state and generational evolutionary algorithm for dynamic multiobjective optimization［J］. IEEE Transactions on Evolutionary Computation， 2017， 21（1）：65-82.

[20] XU B， ZHANG Y， GONG D， et al. Environment sensitivity-based cooperative co-evolutionary algorithms for dynamic multi-objective optimization［J］. IEEE/ACM Transactions on Computational Biology and Bioinformatics， 2018， 15（6）： 1877-1890.

[21] GOH C K， TAN K C. A competitive-cooperative coevolutionary paradigm for dynamic multiobjective optimization［J］. IEEE Transactions on Evolutionary Computation， 2009， 13（1）：103-127.

[22] DEB K， THIELE L， LAUMANNS M， et al. Scalable test problems for evolutionary multiobjective optimization［M］// ABRAHAM A， JAIN L， GOLDBERG R. Evolutionary Multiobjective Optimization： Theoretical Advances and Applications， AI&KP. London： Springer， 2005： 105-145.

[23] ZHOU A， JIN Y， ZHANG Q. A population prediction strategy for evolutionary dynamic multiobjective optimization［J］. IEEE Transactions on Cybernetics， 2014， 44（1）： 40-53.

[24] FARINA M， DEB K， AMATO P. Dynamic multiobjective optimization problems： test cases， approximations， and applications［J］. IEEE Transactions on Evolutionary Computation， 2004， 8（5）：425-442.

[25] DENG H， YEH C H， WILLIS R J. Inter-company comparison using modified TOPSIS with objective weights［J］. Computers and Operations Research， 2000， 27（10）：963-973.

[26] 何春雄，龍衛江，朱鋒峰. 概率論與數理統計［M］. 北京：高等教育出版社， 2012：79-80.（HE C X， LONG W J， ZHU F F. Probability Theory and Mathematical Statistics［M］. Beijing： Higher Education Press， 2012：79-80.）

[27] CAO L， XU L， GOODMAN E D， et al. Decomposition-based evolutionary dynamic multiobjective optimization using a difference model［J］. Applied Soft Computing， 2019， 76： 473-490.

[28] 周永道，王會琦，呂王勇. 時間序列分析及應用［M］. 北京：高等教育出版社， 2015：69-87.（ZHOU Y D， WANG H Q， LYU W Y. Time Series Analysis and Application［M］. Beijing： Higher Education Press， 2015：69-87.）

[29] WANG C， YEN G G， ZOU F. A novel predictive method based on key points for dynamic multi-objective optimization［J］. Expert Systems with Applications， 2022， 190： No.116127.

Dynamic multi-objective optimization algorithm based on adaptive prediction of new evaluation index

LI Erchao*， ZHANG Shenghui

（，，730050，）

Most of the Multi-objective Optimization Problems （MOP） in real life are Dynamic Multi-objective Optimization Problems （DMOP）， and the objective function， constraint conditions and decision variables of such problems may change with time， which requires the algorithm to quickly adapt to the new environment after the environment changes， and guarantee the diversity of Pareto solution sets while converging to the new Pareto frontier quickly. To solve the problem， an Adaptive Prediction Dynamic Multi-objective Optimization Algorithm based on New Evaluation Index （NEI-APDMOA） was proposed. Firstly， a new evaluation index better than crowding was proposed in the process of population non-dominated sorting， and the convergence speed and population diversity were balanced in different stages， so as to make the convergence process of population more reasonable. Secondly， a factor that can judge the strength of environmental changes was proposed， thereby providing valuable information for the prediction stage and guiding the population to better adapt to environmental changes. Finally， three more reasonable prediction strategies were matched according to environmental change factor， so that the population was able to respond to environmental changes quickly. NEI-APDMOA， DNSGA-Ⅱ-A （Dynamic Non-dominated Sorting Genetic Algorithm-Ⅱ-A）， DNSGA-Ⅱ-B （Dynamic Non-dominated Sorting Genetic Algorithm-Ⅱ-B） and PPS （Population Prediction Strategy） algorithms were compared on nine standard dynamic test functions. Experimental results show that NEI-APDMOA achieves the best average Inverted Generational Distance （IGD） value， average SPacing （SP） value and average Generational Distance （GD） value on nine， four and eight test functions respectively， and can respond to environmental changes faster.

dynamic multi-objective optimization; evolutionary algorithm; evaluation index; non-dominated sorting; prediction strategy

This work is partially supported by National Natural Science Foundation of China （62063019）， Natural Science Foundation of Gansu Province （20JR10RA152， 22JR5RA241）.

LI Erchao， born in 1980， Ph. D.， professor. His research interests include multi-objective optimization， artificial intelligence， robot control.

ZHANG Shenghui， born in 1997， M. S. candidate. His research interests include dynamic multi-objective optimization.

1001-9081（2023）10-3178-10

10.11772/j.issn.1001-9081.2022091453

2022?09?30；

2022?11?17；

國家自然科學基金資助項目（62063019）；甘肅省自然科學基金資助項目（20JR10RA152，22JR5RA241）。

李二超（1980—），男，河北保定人，教授，博士，主要研究方向：多目標優化、人工智能、機器人控制； 張生輝（1997—），男，甘肅武威人，碩士研究生，主要研究方向：動態多目標優化。

TP273

A

2022?11?21。