基于改進自抗擾的永磁同步電機控制系統

黃茂源， 吳 一， 王 磊， 代文昭

（西安航天精密機電研究所， 陜西 西安 710100）

0 引言

永磁同步電機（Permanent Magnet Synchronous Motor，PMSM）具有功率密度高、體積小、轉矩電流比高、結構簡單等特點，并且伴隨著電力電子技術、稀土永磁材料等技術的發展， 永磁同步電機控制系統得到了人們越來越多的注視，并被廣泛的使用到機器人、數控機床、航空航天等領域[1]。 由于其非線性強耦合的特性，傳統的PID 控制器無法在控制精度和擾動抵抗等方面達到預期的要求[2]。近年來，滑模控制、自適應控制、滑膜變結構控制等非線性控制策略被提出并應用于永磁同步電機控制[3]。 但這些非線性控制存在對模型精度要求比較高。 自抗擾控制算法是由韓京清院士基于傳統PID 固有缺陷改進提出的一種控制方法[4]，其設計不需要依賴精確的數學模型，核心思想是把系統未建模的內部擾動和未知外部擾動歸結為 “總擾動”來進行觀察額補償[5]。

自抗擾控制器主要包括三個部分：跟蹤微分器（tracking differentiator）、擴展狀態觀測器（extended state observ er）和非線性狀態誤差反饋控制（non-linear state error feedback）[6]。 各部分需要整定的參數隨著階數的增加而增加，影響其在實際應用中的實時性，從而影響控制性能[7]。

本文選擇在電機三環控制中的速度環中采用一階自抗擾控制器。 并基于永磁同步電機旋轉坐標系下數學模型，采用空間矢量脈寬調制技術（SVPWM）對目標電壓進行調制，并利用在Matlab/Simulink 環境下進行仿真實驗，與原速度環的PI 控制進行分析和比較。 實驗結果表明，采用ADRC 控制，永磁同步電機具有更好的穩態性能、動態性能和魯棒性。

1 永磁同步電機數學模型

本文以表貼式永磁同步電機為例， 表貼式永磁同步電機有著d、q 軸電感相等的特點Ld=Lq，為了建立現實可行的數學模型，做如下的假設：

（1）忽略磁飽和、磁滯和渦流因素對電機的影響，假設電機磁路是線性、可疊加的。

（2）轉子上沒有阻尼繞組，永磁體沒有阻尼作用。在此假設下，建立永磁同步電機數學模型如下：

式中：ud，uq—定子電壓矢量的交直軸分量；id，iq—交直軸電流；Ld，Lq—交直軸電感，由于選用表貼式PMSM，其交直軸電感相同，取Ld=Lq=Ls。 ωm、np、J、Ψf分別為機械角速度、極對數、轉動慣量和永磁體磁鏈，Kt、B、TL分別為轉矩常數、摩擦系數和負載轉矩。

為控制簡單，無需考慮id、iq間耦合作用，采用id=0 控制方法，則數學模型如下：

根據自抗控制原理， 將iq作為轉速的被控對象，即ADRC 的輸出，將負載轉矩變化、摩擦系數、直軸電流作為系統的擾動。 將式（1）變形為

觀察式（3），永磁同步電機電流環是一階模型，因此可以設計一階的速度環ADRC 控制器。

2 自抗擾控制器設計

如圖1 所示，為標準的自抗擾控制器原理結構圖，其由跟蹤微分器、擴展狀態觀測器、非線性狀態誤差反饋控制三部分組成。

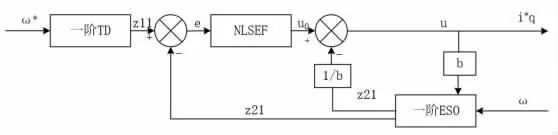
圖1 自抗擾控制原理圖

設一階被控對象為：

式中：x—狀態變量；u—信號輸入；y—信號輸出。

2.1 跟蹤微分器模型

式中：y*—期望輸出；z11—y*的跟蹤信號；fal—非線性最速控制函數，定義為：

式中：α—非線性因子；δ—濾波因子， 最速控制函數有著大誤差小增益，小誤差大增益的特性。其中需要整定的參數為速度因子r，r 的取值越大跟蹤速度越快，但是，r 過大會引入噪聲和大的超調， 因此r 的取值應在保證速度的前提下，取盡可能小的數值。

2.2 擴展狀態觀測器

式 中：z12，z22分 別 為x 和 其 擾 動 值 的 觀 察 信 號；β01，β02是ESO 的增益。 狀態觀測其中有α1、δ1、β01和β02四個參數需要整定。α1一般根據經驗選取0.5。最速控制函數fal 函數線性區間寬度的選取受到系統的誤差范圍的影響， 取值過小會使控制系統產生高頻脈動，取值過大會減弱非線性反饋的效果，一般取值在0.01 左右。 擴展狀態觀測器的增益取值受仿真周期影響， 取值過大則系統調節速度越快，但是取值過大將導致超調。

2.3 非線性狀態誤差反饋控制模型為：

式中：β1是NLSEF 的增益。 NLSEF 共有3 個參數需要整定：α2、δ1、β1， 一般α2選取0～1 之間的數，δ2選取與δ1相同，取0.01 左右。 β1一般采用試湊法進行調節。

根據設計的控制器， 可以得到基于一階速度環的的永磁同步電機系統矢量控制模型，如圖2 所示。

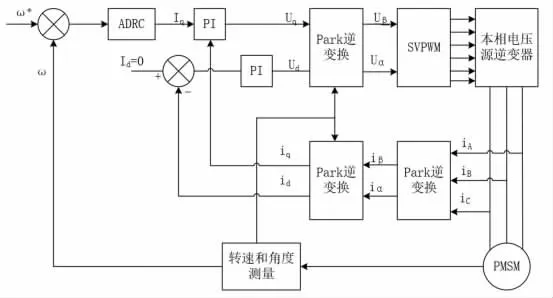
圖2 基于ADRC 的PMSM 控制模型

3 仿真分析

為驗證本文設計的一階自抗擾永磁同步電機控制的可行性和有效性， 本文選擇在Matlab/Simulink 中進行仿真，并與PI 結構進行對比。 電機參數設置如下：極對數Pn=4，定子電感Ld=8.5mH，定子電阻R=2.875Ω，磁鏈Ψf=0.175wb，轉動慣量J=0.001kg·m2，阻尼系數B=0N·M·s。額定轉速n=1000t/min。

在PI 控制系統中， 速度環參數設置為Kωp=0.14，Kωi=7；將兩個電流環PI 控制器設置為相同參數，其中比例增益Kip=1.7，積分增益Kii=287.5。

在永磁同步電機自抗擾控制中， 電流環Kip=1.7，Kii=287.5。一階非線性電流環ADRC 的參數取為：ESO 中α1=0.4，δ1=0.01，β01=300，β02=4000；NLSEF 中：α2=0.5，δ2=0.01，β1=100，b=3200。

仿真時長為0.4 時，為在給定轉速n=1000r/rad，負載轉矩初始時為0.1N·m，在t=0.2s 時跳變為10N·m。 電機的期望轉速設置為ω·r=500r/min，仿真結果如圖3 所示。

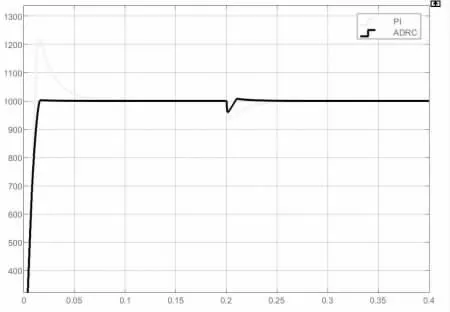
圖3 轉速仿真結果

從圖3 中可以看出，ADRC 控制方法下，電機轉速穩態精度更高。 與傳統PI 控制在啟動時出現一定的振蕩和超調相比，ADRC 在啟動時可以更快速地跟蹤期望轉速，并且更加平穩。 此外，在外部出現負載突變時，恢復到期望轉速的速度更快。

圖4 對兩種策略下電磁轉矩進行分析，其中PI 策略下的電磁轉矩的脈動約為0.21N·m， 而ADRC 策略下的電磁轉矩脈動約0.11N·m。 與PI 控制策略相比較， 自抗擾控制策略下的電磁轉矩脈動更小， 且當電機啟動時以及負載突變時，ADRC 轉矩的輸出更為平滑，具有更小的振蕩。

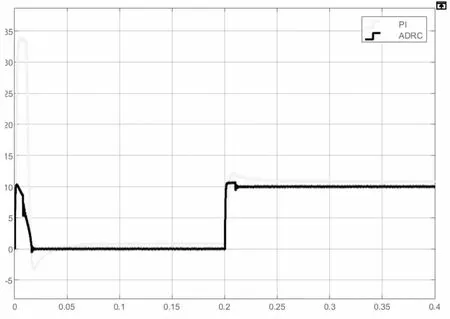
圖4 加入負載后轉矩變化

4 結束語

本文將PMSM 傳統速度環中的PI 控制用一階ADRC替換。 實驗證明，一階ADRC 比傳統的PI 控制有著更好的動態性能和抗擾動能力。并且，簡化后的自抗擾控制器具有結構更簡單，待整定參數少等優點。為其他自抗擾的應用提供了相應的參考。