某SUV 麥弗遜前懸架客觀測試與ADAMS/Car 懸架K＆C特性符合性研究

顏 松， 劉 延， 華 鋒

（中國汽車工程研究院股份有限公司， 重慶 404100）

0 引言

懸架系統作為汽車底盤行駛系的關鍵組成元件，其優劣直接決定了汽車的操縱穩定性、 乘坐舒適性等重要的底盤行駛性能。在眾多懸架形式中，麥弗遜懸架以其結構簡單，質量輕、響應速度快等優點被廣泛應用于乘用車前懸架[1]。該類懸架的車輪定位參數（車輪外傾角、車輪前束角、主銷內傾角、主銷后傾角等）對汽車的直線行駛性能、輪胎磨損和方向盤的回正性都有著重要的影響[2]。

本文基于某SUV 麥弗遜前懸架車輪同向跳動和異向跳動試驗工況， 重點分析車輪前束角和車輪外傾角的變化梯度， 并對這2 個車輪定位參數的仿真結果和客觀測試結果的符合性進行研究，分析了車輛懸架特性KC 仿真結果和客觀測試數據之間的差異及原因， 并對懸架硬點進行了優化。

1 競品車型麥弗遜前懸架選型要求及優化流程

一般而言， 麥弗遜前懸架競品車型選擇應滿足以下要求[3-6]：

（1）市場占有率較高。

（3）懸架結構緊湊、操縱穩定性好。

（4）懸架具備良好的隔音、吸振和減振性能。

（5）懸架具有足夠的壽命、剛度和強度、質量輕。

（6）懸架零部件制造成本低，售后維護成本低，輪胎磨損小。

麥弗遜前懸架優化流程如圖1 所示。

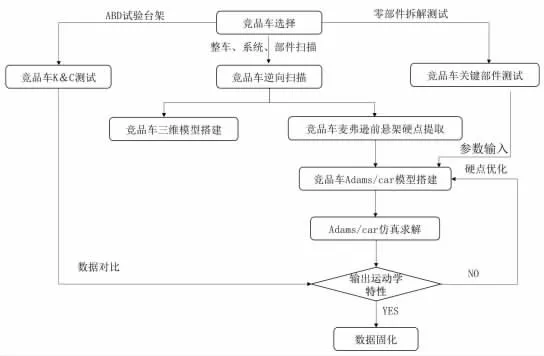
圖1 麥弗遜前懸架優化流程圖

2 整車前懸架結構圖及主要參數

本文研究的某SUV 的麥弗遜前懸架結構圖如圖2 所示。 整車主要參數、前懸架初始硬點坐標、前懸架關鍵零部件重量及轉動慣量分別見表1～4。

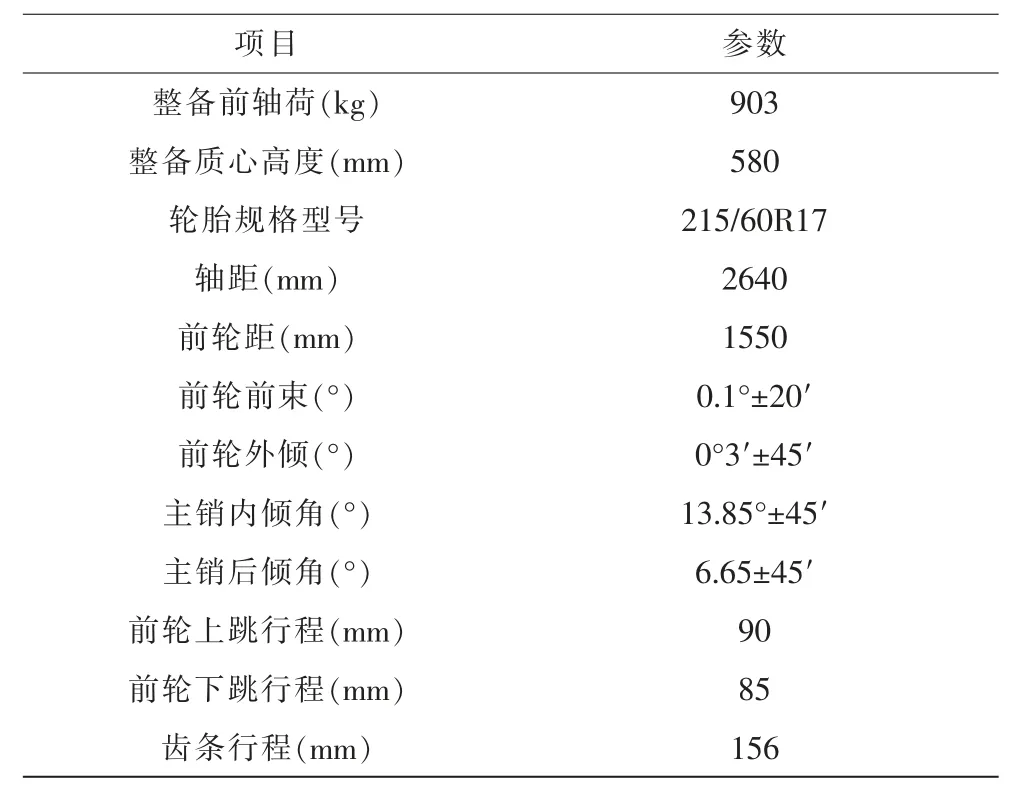
表1 整車主要參數

表4 前懸架關鍵零部件轉動慣量

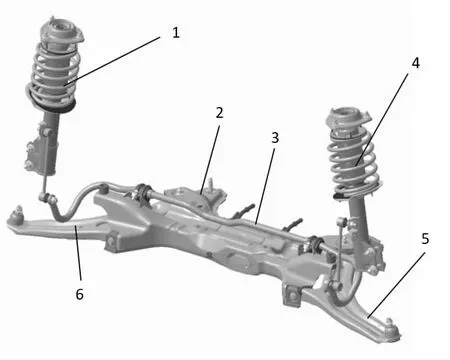
圖2 某SUV 麥弗遜前懸架結構圖

前懸架襯套減振器阻尼參數分別見圖3～6。

我們以詞匯的學習策略為例，英語中詞匯的學習一直是學習者的難點。其實英語單詞的構成是有規律的，掌握了構詞規律，才可以準確快速地記憶單詞。英語單詞構詞法的核心部分在于詞根，詞的意義主要是由組成單詞的詞根體現出來的，通過前綴后綴來改變單詞的詞性和意義（詞根和詞綴叫構詞語素）。也就是說，單詞一般由三部分組成：詞根、前綴和后綴。詞根決定單詞意思，前綴改變單詞詞義，后綴決定單詞詞性。

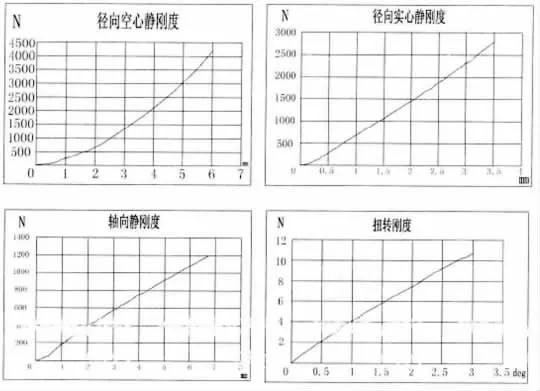
圖3 左前下控制臂前襯套阻尼曲線

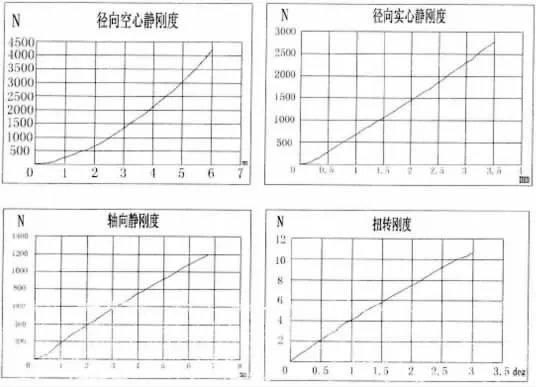
圖4 左前下控制臂后襯套阻尼曲線

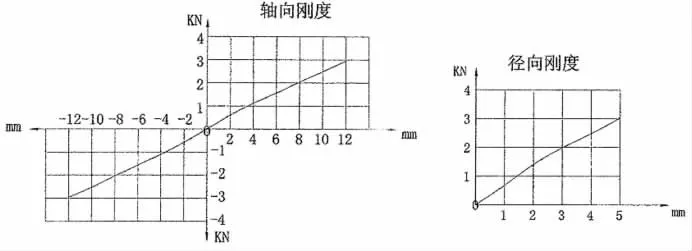
圖5 左前減振器上膠套阻尼曲線

3 前懸架實測關鍵K＆C 值及合理區間

3.1 左右車輪同向跳動

麥弗遜前懸架車輪同向跳動前束變化梯度同類車型合理區間范圍在-0.009deg/mm～-0.0003deg/mm 之間。 如圖7 所示，該SUV 麥弗遜前懸架左右車輪同向跳動左前束變化梯度為-0.007981deg/mm，在合理區間范圍內。

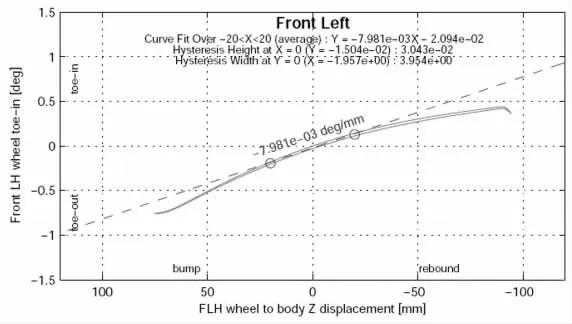
圖7 車輪同向跳動左前束變化梯度整車實測曲線圖

同類車型麥弗遜前懸架車輪同向跳動外傾變化梯度合理區間范圍在-0.016 deg/mm～-0.0005 deg/mm 之間。如圖8 所示，該SUV 麥弗遜前懸架車輪同向跳動左外傾變化梯度為-0.005956deg/mm，在合理區間范圍內。

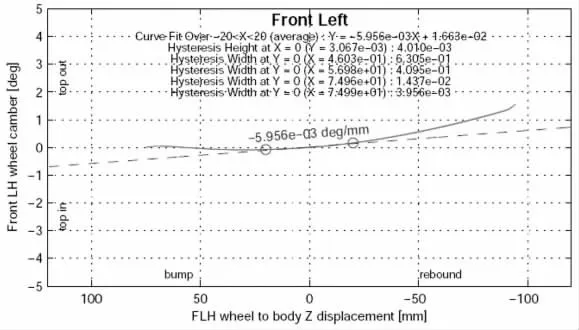
圖8 車輪同向跳動左外傾變化梯度整車實測曲線圖

3.2 左右車輪異向跳動

同類車型麥弗遜前懸架側傾工況前束梯度合理區間范圍在-0.03deg/mm～0.08deg/mm 之間。 如圖9 所示，該SUV 麥弗遜前懸架側傾工況左輪前束變化梯度為-0.007088deg/mm，在合理區間范圍內。

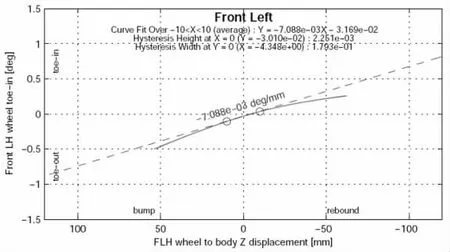
圖9 側傾工況左輪前束變化梯度整車實測曲線圖

同類車型麥弗遜前懸架側傾工況外傾梯度合理區間范圍在-0.9deg/mm～0.5deg/mm 之間。 如圖10 所示，該SUV 麥弗遜前懸架側傾工況左輪外傾變化梯度為0.07561deg/mm，在合理區間范圍內。

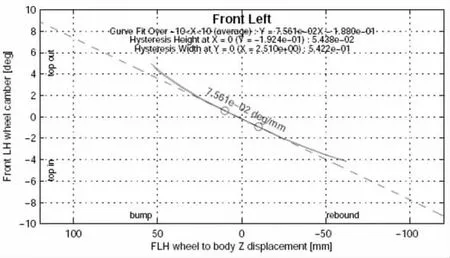
圖10 側傾工況左輪外傾變化梯度整車實測曲線圖

4 前懸架初始硬點ADAMS 多體動力學模型建模及仿真分析

在ADAMS/Car 軟件環境中建立初始硬點ADAMS 麥弗遜前懸架模型[7-9]，如圖11 所示。分別進行平行輪跳試驗和異向輪跳加載仿真試驗，麥弗遜前懸架仿真曲線圖中，實線為初始硬點懸架左邊的仿真曲線， 虛線為實車測試K＆C 曲線。

圖11 初始硬點ADAMS 麥弗遜前懸架模型

4.1 左右車輪平行跳動時懸架的運動特性分析

同向輪跳使左右輪相對平衡位置同時上下運動，在仿真分析時， 車輪跳量設置為-85mm～90mm， 仿真步數為100 步[7]，在后處理中根據硬點優化需要，重點分析合理輪跳行程區間±25mm內麥弗遜前懸架車輪前束角和車輪外傾角梯度變化。

從圖12 可以看出，懸架前束隨輪跳上行程逐漸減小。當汽車轉彎行駛時， 懸架內外側分別受到拉伸和壓縮，懸架前束會產生對應的變化，使前輪形成一定的轉角并削弱原來的轉向，即會導致前束角隨輪跳變化出現不足轉向的趨勢。此外，輪胎偏磨與前束也有一定關系，車輛行駛過程中，如果前束的變化梯度過大，會影響車輛的直線行駛穩定性，同時增大輪胎與地面間的滾動阻力，加劇輪胎的磨損，因此前束的設計原則是當車輪跳動時，前束的變化量越小越好[10]。 如圖12 所示，前束變化梯度為-0.0069deg/mm，在同類車型合理區間范圍-0.009deg/mm～-0.0003deg/mm 之內， 和實測前束變化梯度-0.007981deg/mm 相差較小，但是初始硬點仿真曲線和整車實測曲線在±25mm 行程范圍內貼合率較低，需要進行硬點優化。

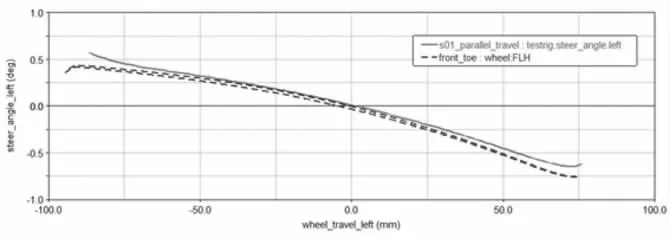
圖12 車輪同向跳動左前束變化梯度初始硬點曲線圖

從圖13 可以看出，外傾角隨車輪上跳逐漸減小。 當車輛轉彎行駛時，車身外側車輪上跳，相對于地面向正外傾角方向變化，從而降低了承載較高一側輪胎的側偏性能，內側車輪則相反。這種特性有利于轉向過程中的外傾車輪保持垂直以增加轉向附著能力[11]。 同時，車輪上跳及回落時的產生的外傾角變化直接影響汽車的直線行駛穩定性；車輛直行時， 路面的激勵使車輪跳動導致其外傾角變化時，會產生橫向作用力，因而較大的對地外傾變化會影響車輛直線行駛穩定性。 如圖13 所示，外傾角變化梯度為-0.0079deg/mm，在同類車型合理區間范圍-0.016deg/mm～-0.0005deg/mm 之內，和實測外傾角變化梯度-0.005956deg/mm相差較小，但是初始硬點仿真曲線和整車實測曲線在±25mm行程范圍內貼合率較低，需要進行硬點優化。

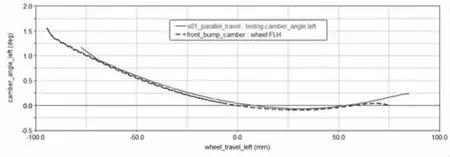
圖13 車輪同向跳動左外傾變化梯度初始硬點曲線圖

4.2 左右車輪異向跳動時懸架的運動特性分析

異向輪跳使左右輪相對平衡位置同時上下運動，在仿真分析時，車輪跳量設為-50mm～50mm。

對于左輪，當車輛右轉彎行駛時，左右側車輪會分別受到壓縮和伸張，產生正的側向力，車輪受到的側向力變大， 導致前束變小， 這種變化趨勢會減少汽車轉向的程度，右輪類似。 在側向力作用下車輛具有不足轉向趨勢，有利于整車的穩態轉向。 如圖14 所示，前束隨車輪上跳逐漸減小，其變化梯度為-0.0061deg/mm，在同類車型合理區間范圍-0.03deg/mm～0.08deg/mm 之內， 和實測前束變化梯度-0.007088deg/mm 相差較小，但是初始硬點仿真曲線和整車實測曲線在±25mm 行程范圍內貼合率較低，需要進行硬點優化。

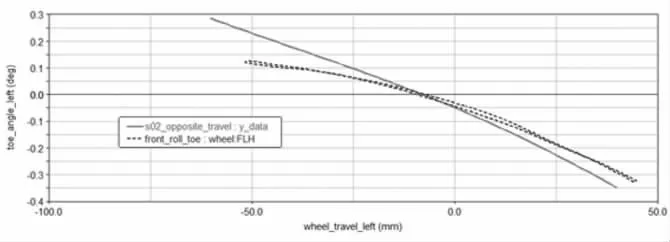
圖14 車輪異向跳動左前束變化梯度初始硬點曲線圖

對于左輪，當車輛右轉彎行駛時，會產生正的側向力，車輪受到的側向力變大，導致車輪外傾角變大，這種變化趨勢會減少汽車轉向的程度，右輪類似。即左輪外傾隨側向力加大而增大，而右輪外傾角隨側向力加大而減少[10]。 如圖15 所示，外傾角隨車輪上跳也逐漸減小，其變化梯度為-0.0105deg/mm， 在同類車型合理區間范圍-0.9deg/mm～0.5 deg/mm 之內， 和實測前束變化梯度0.07561deg/mm 偏差較大， 且初始硬點仿真曲線和整車實測曲線在±25mm行程范圍內貼合率較低，需要進行硬點優化。

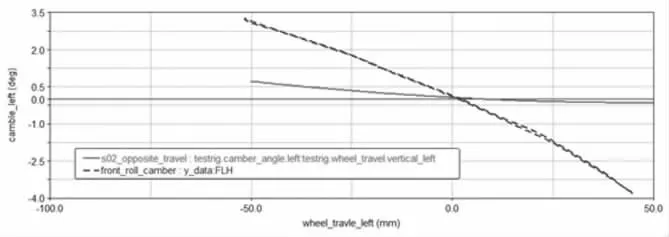
圖15 車輪異向跳動左外傾變化梯度初始硬點曲線圖

車輪外傾角和前束對汽車的直線行駛穩定性、 轉向穩態回正特性和輪胎磨損均有較大的影響， 一般希望懸架前束和懸架外傾變化越小越好。從以上對比可以看出，從多體動力學模型中得到的車輪外傾角和車輪前束角變化和運動學模型中得到結果偏差較大， 且曲線貼合率不高，需要對某初始硬點進行優化。

5 前懸架優化硬點ADAMS 多體動力學分析

基于以上對比分析， 在ADAMS/Insight 模塊中對前懸架硬點進行優化，優化后的硬點坐標見表5。

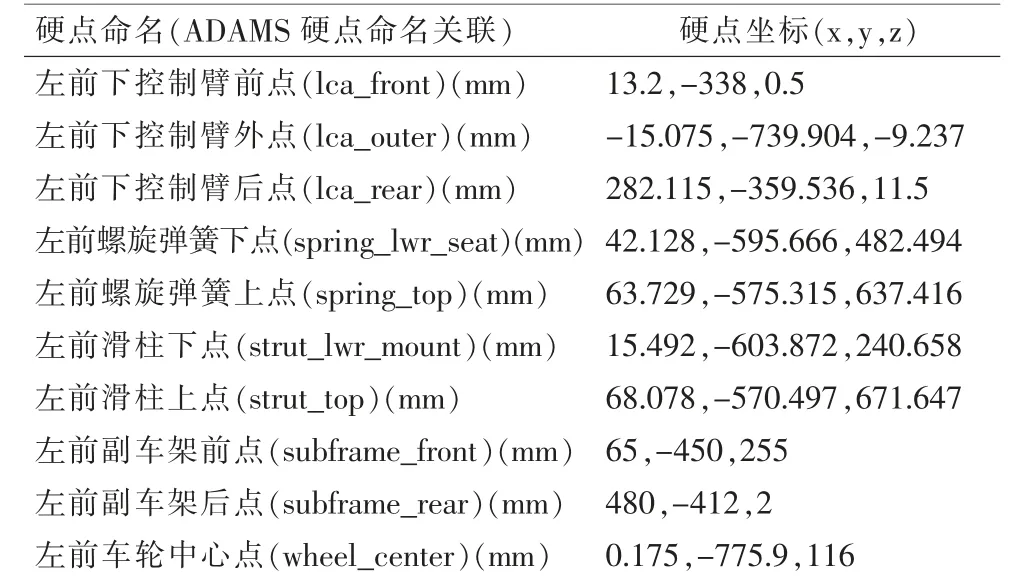
表5 前懸架最終硬點坐標

硬點優化后， 左右車輪平行跳動和異向跳動時懸架的運動特性如圖16～19 所示。

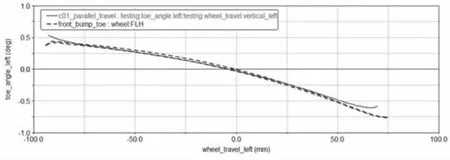
圖16 車輪同向跳動左前束變化梯度優化硬點曲線圖

從圖16 可以看出，硬點優化后，同向跳動時前束變化梯度為-0.0074deg/mm， 在同類車型合理區間范圍-0.009 deg/mm～-0.0003 deg/mm 之內，且和實測前束變化梯度0.007981deg/mm 相差較小，優化硬點仿真曲線和整車實測曲線在±25mm 行程范圍內貼合達到95%以上，優化較為合理。

從圖17 可以看出，硬點優化后，同向跳動時外傾變化梯度為-0.0052deg/mm，在同類車型合理區間范圍-0.016 deg/mm～-0.0005 deg/mm 之內，且和實測外傾變化梯度0.005956deg/mm 相差較小，優化硬點仿真曲線和整車實測曲線在±25mm 行程范圍內貼合達到95%以上，優化較為合理。

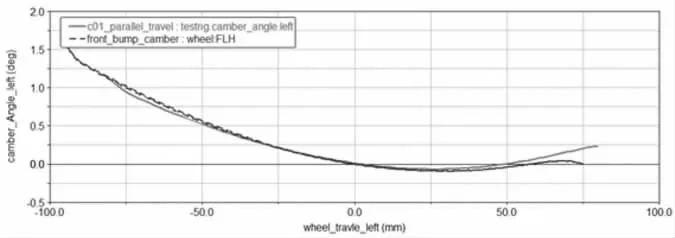
圖17 車輪同向跳動左外傾變化梯度初始硬點曲線圖

從圖18 可以看出，硬點優化后，異響跳動時前束變化梯度為0.0068deg/mm，在同類車型合理區間范圍-0.03deg/mm～0.08 deg/mm 之內，和實測值0.007088deg/mm相差較小，優化后硬點仿真曲線和整車實測曲線在±25mm行程范圍內貼合達到95%以上，優化較為合理。

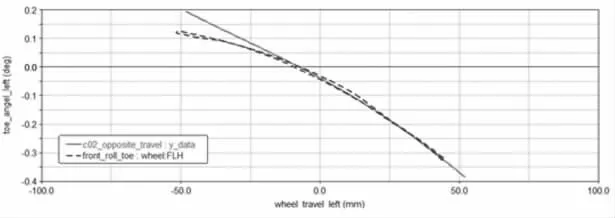
圖18 車輪異向跳動左前束變化梯度優化硬點曲線圖

從圖19 可以看出，硬件優化后，異向跳動時外傾變化梯度為0.068deg/mm，在同類車型合理區間范圍-0.9deg/mm～0.5deg/mm 之內，和實測前束變化梯度0.07561deg/mm 偏差較小， 優化后硬點仿真曲線和整車實測曲線在±25mm行程范圍內貼合達到95%以上，優化較為合理。

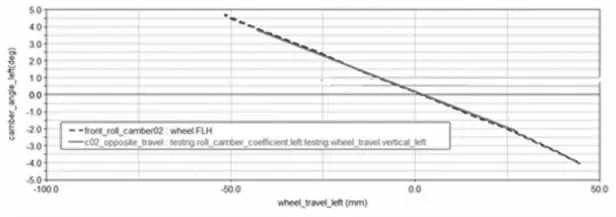
圖19 車輪異向跳動左外傾變化梯度優化硬點曲線圖

6 結束語

本文重點對懸架系統KC 仿真結果和客觀測試結果的符合性進行了研究， 分析了車輛懸架特性KC 仿真結果和客觀測試數據之間的差異及原因， 在ADAMS/Car 軟件環境中建立初始硬點麥弗遜前懸架模型并進行優化，硬點優化后的仿真分析結果和競品車實測曲線貼合度達到95%以上，且變化梯度處于較為合理的目標區間，優化較為合理，對拓展車型開發操縱穩定性數學模型提供了可靠的理論依據以保證模型能夠準確的預測汽車的動力學性能，從而有利于減少整車試驗，縮短前懸架的開發周期。