船用汽輪機轉速線性自抗擾控制研究

張榮彬，郭永飛

（中廣核研究院，廣東 深圳 518000）

0 引言

隨著國家海洋強國戰略的推進，船用核動力裝置的研究發展迅速。汽輪機作為船用核動力裝置的核心設備，其控制性能的好壞直接影響船舶的機動性和安全性，尤其近年來孤網技術的發展，對船用核動力裝置及其參與孤網發電的汽輪機調節提出了更高的要求。由于孤網的抗擾動能力差且負荷波動范圍大，對機組一次調頻的靈敏度、調節幅度及響應速度要求高[1]，且船用汽輪機調速系統中常包含死區、慣性等非線性環節，采用傳統的線性PID 控制較難保持良好的控制性能。

目前，國內外眾多學者對汽輪機轉速控制系統的設計展開了廣泛研究。王元慧[2]等針對船用核動力裝置設計了串級前饋-反饋模糊PID 控制，實現汽輪機轉速的穩定控制；李明輝[3]等采用模糊控制和內模控制相結合的方法，通過粒子群算法對控制器參數自適應調整，有效提高了汽輪機調速系統的響應速度和抗擾性能；楊旭紅[4]等針對核電站汽輪機轉速控制系統中的不確定性和非線性，運用改進的PSO 算法對PID 控制器參數進行優化設計，該方法增強了系統穩定性，具有響應速度快，超調小等優點，明顯改善了汽輪機轉速的控制品質；詹錦皓[5]等提出基于串級前饋PID 協調控制的汽輪轉速控制系統，采取負荷變化量作為前饋控制，在故障情況仍可維持汽輪機轉速穩定，具有較好的容錯性。可見，設計結構簡單、抗干擾能力強、魯棒性好，且不依賴于系統精確模型的控制器，提高了汽輪機轉速控制性能，對于船用核動力裝置工程的實踐應用有著重要意義。

自抗擾控制（active disturbance rejection control,ADRC），其核心是將被控對象自身的不確定性與外部干擾一并視作“總擾動”[6]，利用擴張狀態觀測器（extended state observer，ESO）進行實時估計并補償自抗擾控制作為一種先進控制算法，不僅具備PID 控制結構簡單的優點，且不依賴精確的系統模型，但由于其參數過多導致整定困難，實踐中未能廣泛應用。為此，Gao[7]提出將非線性ADRC簡化為線性形式（linear active disturbance rejection control，LADRC），使控制器參數得以簡化，同時又繼承了ADRC的優點。研究表明[8]，通過設計合適的LADRC 結構，調整線性擴張狀態觀測器（LESO）的帶寬，可有效提高系統控制性能。

本文提出一種基于線性自抗擾控制的汽輪機轉速控制策略，以優化數字電液系統控制性能。通過建立船用汽輪機的數學模型，采用MWorks 軟件的Sysplorer 仿真環境，搭建基于LADRC 的汽輪機調速系統模型。仿真結果表明，此方法具有穩態誤差小、響應速度快、超調小等優點，明顯改善了汽輪機轉速的控制品質。

1 船用汽輪機調速系統建模

根據汽輪機調速系統的工作原理，船用汽輪機轉速控制系統一般可簡化為由調速器、控制器、電液轉換器、油動機、蒸汽容積、轉子6 部分構成的數學模型。

1.1 調速器數學模型

由于制造工藝的不斷完善，調速器質量和摩擦阻尼可忽略不計。本文采用理想的調速器模型，即：

式（1）中：δ為汽輪機轉速不等率；ζ為調速器滑環位移變化相對值；φ為轉速變化的相對值。其傳遞函數可表示為比例環節：

1.2 電液轉換器數學模型

電液轉換器是將電信號控制指令轉換、放大為液壓信號，由油動機去控制調節閥，實現自動調節。電液轉換器模型可表示為電液轉換器滑閥位移Xv對力矩馬達電壓U 的傳遞函數

式（3）中：Ka為伺服放大器增益；Kxv為伺服閥增益；Kvf為力反饋回路的開環放大系數；ωmf為力矩馬達固有頻率；ζmf為力矩馬達的阻尼比。當力矩馬達的固有頻率ωmf足夠大時，在仿真過程中對各物理變量進行無量綱化處理，則電液轉換器的傳遞函數可以簡化為

式（4）中，Te為電液轉換器時間常數。

1.3 油動機數學模型

油動機為汽輪機調節系統中驅動調節汽閥的執行機構，本文所采用的油動機類型為單側進油閥油動機。當滑閥移動時，油動機的進油流量為

式（5）中，μ為油口的流量系數；Xv為滑閥的位移變化量；b為油口的寬度；ρ為壓力油密度；p0為進油壓力；p1為進入活塞底部后油的壓力。油動機排油流量與進油流量相等，忽略油運動的慣性力，并將進油量等效為單位時間內活塞移動掃過的體積，可得活塞行程的變化率為

式（6）中：pd為出口油壓力；A 為進油側活塞有效面積。進而，油動機的傳遞函數可以簡化為

式（7）中：Tc為油動機的時間常數。

1.4 蒸汽容積數學模型

假設蒸汽流經體積為V的容器，根據氣體流動的連續方程，可以得到進、出口流量的變化量與容積內質量的關系表達式為

式（8）中：q1和q2分別為進口和出口流量，kg/s；ρ1為蒸汽密度，kg/m3。對式（8）進行泰勒展開并略去其高階項，考慮到蒸汽容積的氣體噴口面積不變，可得到穩定狀態下氣體體積變化量Xs1，進而推導得到蒸汽容積傳遞函數為

式（9）中：Xp為壓力相對變化量；Tρ為進汽容積時間常數。

1.5 轉子數學模型

影響汽輪機轉子運動的因素有汽輪機的蒸汽轉矩MT，負載的反轉矩ML，摩擦轉矩Mf。由于Mf遠遠小于MT和ML，可以將其忽略，因此轉子的力平衡方程為

式（10）中，J為轉子的轉動慣量；ω為轉子角速度。再由蒸汽壓力與轉子角速度關系和角速度與時間的關系，同時忽略轉子的自平衡能力，可得轉子傳遞函數表達式為

式（11）中，Td為轉子時間常數。

2 線性自抗擾控制器設計

LADRC 主要由線性狀態觀測器（LESO）和線性狀態誤差反饋控制律（LSEF）兩個部分組成。典型二階系統的LADRC 控制器基本結構如圖1 所示。

圖1 LADRC基本結構Fig.1 Basic structure of LADRC

圖1 中，r-設定值信號；u0-LSEF 計算輸出信號；u-控制輸出；z1-輸出信號（y）的觀測值；z2-y 的一階微分的觀測值；z3-總擾動的觀測值。

2.1 線性擴張狀態觀測器

一般地，考慮二階系統：

式（12）中：u為系統輸入；y為系統輸出；b為控制增益；w為系統不可測擾動；f為系統內外部擾動的總和。令x1=y，x2=，x3=f，假設f可微，定義3=h，將式（12）用狀態空間表示為

式（13）中，x為系統狀態變量，y是輸出。式（13）可寫成以下方程組形式：

建立線性擴張狀態觀測器（LESO）[7]：

式（15）中，z為x的觀測值；為LESO 的輸出；L為觀測器增益向量，可通過極點配置等方法來獲得：

式（16）中：ω0為LESO 的帶寬，選取合適的觀測器帶寬，LESO 就能夠實現對式（14）中各變量的實時跟蹤。

2.2 擾動補償

控制器控制量設計為

將式（17）代入式（12）中，并忽略z3對f(y,,w)的誤差，即式（12）可簡化為一個雙積分串聯結構：

這樣通過LESO 即可對系統總擾動進行觀測，并在其對系統產生影響之前進行補償。

2.3 線性狀態誤差反饋控制

在對擾動進行補償之后，再對被控對象施加控制律：

式（19）中：r為給定信號；kp、kd為控制器增益，根據式（18）～式（19）可得系統閉環傳遞函數為

式（20）中的特征多項式表示為：

式中，kp=ωc2，kd=2ζωc，定義ωc為控制器的帶寬，則ωc為控制器中唯一需要整定的參數。

2.4 控制器參數整定

根據前文分析，LADRC 主要參數為觀測器帶寬ω0、控制器帶寬ωc、補償系數b0。控制器參數一般是根據對研究對象的了解，憑經驗進行調節，但在實際整定過程中遵循以下規律[9]：

1）ω0越大，LESO 的響應越快，但這會使觀測器對噪聲更加敏感。因此，首先賦予ω0一個較小的值，然后逐漸增大至觀測精度滿足要求為止。

2）ωc越大，系統輸出響應越快，控制作用越強。當ω0與ωc的比值越大，系統的相角裕度越大，系統越穩定。增加ω0值或者ωc值都會引起高頻帶增益變大，系統的抗噪聲能力下降。

3）當系統遲延較大時，一般選取較小的b0值。在觀測向量z3產生變化時，可使擾動補償(u0-z3)/b0變化更加靈敏，從而快速調節系統的輸出量。

應在保證控制系統穩定的前提下，進行多次試驗和誤差指標對比，最終確定合適的控制器參數。

3 仿真分析

為驗證本文所提出的基于LADRC 的船用汽輪機轉速控制的有效性，在MWorks/Sysplorer 仿真平臺建立汽輪機調速系統模型和LADRC 控制器，開展汽輪機轉速LADRC控制系統仿真驗證，并與經典PID 控制方法進行對比。汽輪機轉速LADRC 控制系統結構如圖2 所示。

圖2 汽輪機轉速LADRC控制系統框圖Fig.2 Block diagram of LADRC control system for turbine speed

采用文獻[10]方法對某船用核動力裝置汽輪機調速系統參數進行辨識，得到模型參數見表1。

表1 汽輪機調速系統模型參數Table 1 Model parameters of steam turbine speed regulation system

3.1 汽輪機轉速指令跟蹤性能對比

為檢驗本文所設計的汽輪機轉速控制系統輸出跟蹤轉速指令信號的性能，在沒有外部擾動的情況下，分別在傳統PID 和LADRC 轉速控制系統輸入端加入階躍信號，采用固定步長0.01s 進行仿真，考察系統輸出跟蹤轉速指令信號的快速性和準確性。PID 參數設置為kp=10、ki=1、kd=1；LADRC 控制器參數設置為ω0=5、ωc=20、b0=0.4。兩種控制系統轉速指令階躍變化時的輸出響應仿真結果如圖3 所示，控制器的性能評估結果見表2。從圖3 和表2 可以看出，傳統PID 控制調節時間長，超調量大，上升時間慢；而采用LADRC 控制器時，控制系統的輸出能夠快速、準確地跟蹤輸入指令，并且快速穩定到設定值，其上升時間減少了1.74s，超調量則減少了7.2%，且提前17.55s 到達穩定。

表2 控制器性能評估結果Table 2 Performance evaluation results of controller

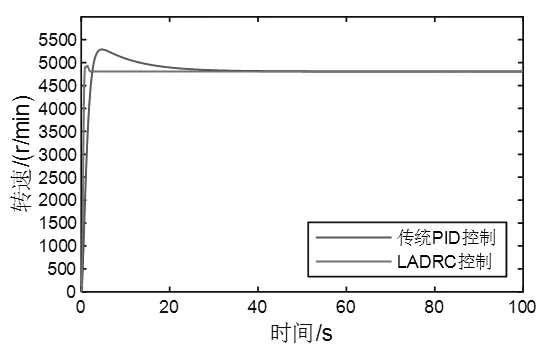
圖3 汽輪機轉速指令階躍特性曲線Fig.3 Step characteristic curve of turbine speed command

3.2 汽輪機抗擾性能對比

為驗證所設計的控制器的抗擾效果，在60s 時加入20%的閥位階躍擾動，系統響應如圖4 所示。在60s 時加入甩100%負荷的階躍擾動，系統響應如圖5 所示。從圖4和圖5 可見，在引入閥位擾動和甩負荷擾動情況下，采用LADRC 控制方案轉速飛升幅度更小，且更快恢復穩定，說明LESO 對擾動的補償估計能夠更好地抑制擾動，提升控制系統的抗擾性能。

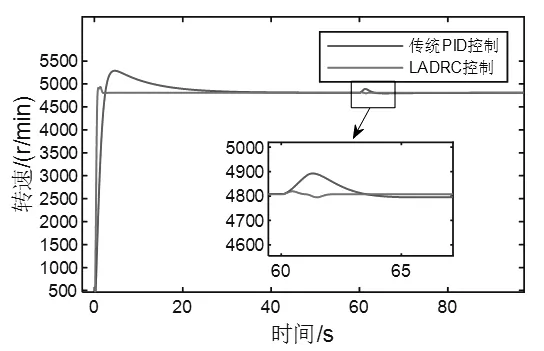
圖4 汽輪機閥位擾動下仿真結果Fig.4 Simulation results of steam turbine valve position disturbance

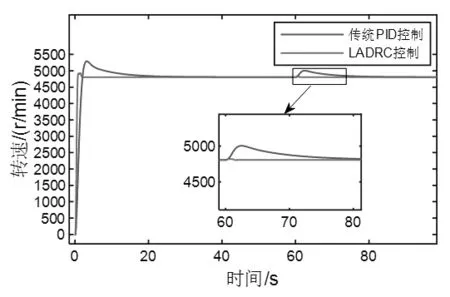
圖5 汽輪機甩負荷時仿真結果Fig.5 Simulation results of turbine load rejection

4 結語

本文研究了孤網模式下船用汽輪機轉速的線性自抗擾控制策略，通過理論推導和系統辨識建立了汽輪機轉速控制系統的數學模型。分別對PID 控制和LADRC 控制系統進行了設定值跟蹤性能和抗擾性能對比實驗，仿真結果表明：

1）相比傳統PID 控制，采用LADRC 的船用汽輪機轉速控制超調量更小、調節時間更短，具有較好的動態響應特性和穩態特性。

2）LADRC 控制器有較好的抗干擾性能，線性擴張狀態觀測器的引入使得LADRC 對外界的干擾起到較好地抑制作用。