基于彈性地基梁理論的公路隧道縱向響應分析

陳宜濃

(兩當縣交通運輸局,甘肅 兩當 742400)

0 引言

中國地貌總體呈現出西高東低、階梯式的特點,且山地廣泛,層巒疊嶂,這嚴重制約著中國城市的快速發展和交通的便利,而隧道是解決這一問題的有效辦法,是中國交通基礎設施建設的最佳選擇[1]。近年來我國基礎建設得到了前所未有的大力開發和高速發展,隧道工程的設計理念及施工經驗不斷積累。但修建隧道的路線也會不可避免的需要穿越各種類型的破碎帶,因此,穿越活動斷層隧道成為我國隧道工程中亟需解決的問題。

針對穿越活動斷層的隧道相關問題,國內外學者進行大量的研究,取得了長足的發展。Rodger[2]通過對美國斷層的研究,對其錯動模型和邊界條件進行假設,為了更形象的表示圣安德里斯斷層,采用了一組直立斷層段近似模擬該斷層,并對其進行分析,結合解析法疊加的方法獲得斷層應力場的變化量等相關參數。張超等[3]重點研究了斷層應力集中,運用解析方法展開論述,為中國的跨斷層隧道參數設計引入了一個新的理論依據。韋良喜等[4]確定了早子溝斷裂構造在多期構造活動下的斷層主應力方向。在構造分析和節理分析研究的基礎上,利用斷層劃痕圖像法和吳氏網絡投影技術對現場觀測記錄和衛星投影圖像進行了分析,最后得出結論。焦鵬飛等[5]對穿越逆斷層的隧道進行研究,運用FLAC3D軟件分析其受力模式及變形規律,最終得出結論,隧道穿越逆向斷層時,擠壓應力作用于隧道結構,拉應力和剪應力集中出現在二襯的拱腰處,這一結論表示隧道的最不利受力狀態為隧道邊墻。閆高明等[6]利用振動臺實驗,在兩種加載形式下分析二襯結構的變形及內力變化規律,分別將單一斷層錯動及斷層錯動+地震波加載,最終實驗結果表明,二襯結構在有分段接頭鉸接的設計時,能夠起到抑制變形的作用,使得隧道在穿越斷層時,其抗震-抗錯斷能力增強。

綜上所述,目前對隧道穿越活動斷層的研究主要聚焦于數值模擬和模型試驗上,對于理論推導的研究尚有不足。鑒于此,本文依托某在建公路隧道,基于彈性地基梁理論,研究了彈性地基梁理論在分析隧道結構變形和內力重分布方面的適用性,以期對此類問題提供一些參考。

1 彈性地基梁理論

彈性地基梁是指支承于地基上的梁[7],梁的每個點都緊密地附著在基礎上,基礎對梁的約束具有一定的彈性,是土木工程中常見的一種結構形式,如鐵路下的枕木、條形基礎等。彈性地基梁與普通梁具有明顯的區別[8]:

1)超靜定是有限還是無限是彈性地基梁與普通梁的主要區別。由于彈性地基梁各個點都與基礎緊密相連,具有無數個支座,因此,彈性地基梁是無限次超靜定結構;而普通梁只在有限次支座上與基礎連接,是靜定的或有限次超靜定結構。

2)地基變形是否考慮是彈性地基梁與普通梁的另一個區別。普通梁只考慮梁的變形,忽略地基的變形,其支座通常被認為是剛性支座;彈性地基梁則不僅需要考慮梁的變形,還需要同時考慮地基的變形。

2 彈性地基梁撓度曲線微分方程求解

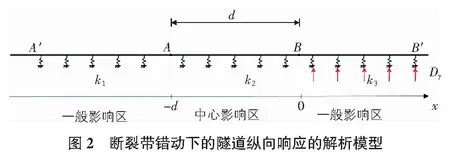
根據地震相關研究的分析和實驗室模型試驗的結果,隧道隨斷層位移的一般反應如圖1所示。地殼運動發生的斷裂會將巖石分為上下兩盤,兩盤之間的相對位移值即為斷層的位移量。在距離斷層區一定距離之外,隧道跟隨周圍巖石的運動,兩者之間不存在相對位移量。與斷層上下盤的巖石相比,活動斷層范圍內的圍巖巖性比較差,結合圖1,可以看出隧道結構變形的基本規律,隧道可以從縱向劃分為三個區:非影響區、一般影響區和中心影響區。由圖1可知,穿越斷層的隧道在AB段變形最大,這一區域屬于中心影響區,這表明巖石發生斷裂,隧道的彎曲變形在此段增加。非影響區(圖1中A′A段)的隧道和圍巖的變形與內力不受活動斷層區面積的影響,中心影響區和非影響區之間的區域為一般影響區(圖1中BB′段)[9]。

以圖1隧道結構在活動斷層錯動作用下的響應特點為依據,本文構建了斷層錯動下隧道縱向響應的解析模型,如圖2所示,為簡化計算,求解解析計算模型時假設以下條件:

1)視隧道結構為連續的,各向同性的均勻介質。2)隧道與圍巖的相互作用可用Pasternak雙參數彈性地基梁模型描述。3)假設斷層活動盤的位移速率足夠低,因此可以將隧道和周圍巖石之間的慣性作用忽視,同時也不考慮隧道縱向分量的影響。4)不考慮隧道的原始應力狀況,僅對隧道位移產生的內力及位移增加進行計算。斷層的活躍位移使巖體的位移和內力增量符合一定的線性變化規律。

Pasternak雙參數彈性地基梁[10]的撓曲線微分方程為式(1):

(1)

其中,k,G,EI分別為地基系數,N/m3;圍巖的垂直剪切模量,N/m;梁的抗彎剛度,N·m2;b為長梁寬度,m;q(x)為梁外均布荷載,N/m。

令(式(2)):

(2)

式(1)可簡化為式(3):

(3)

當外部荷載q(x)為0時,可以將撓曲線微分方程公式(1)簡化為公式(4):

y=eφx(C1cosωx+C2sinωx)+

e-φx(C3cosωx+C4sinωx)

(4)

其中,C1,C2,C3,C4均為待定系數;φ,ω均為地基梁模型彈性特征參數,其表達式為式(5):

(5)

2.1 活動性斷裂帶錯動下的隧道縱向響應解析解

根據圖2所示的解析模型,假設計算模型滿足Winkler-Pasternak的雙參數彈性地基模型,當發生斷層錯動時,上、下兩盤之間的相對位移用Dy(單位:m)表示,模型中BB′為一般影響區,其發生的位移量為Dy,沿隧道延伸方向為x軸,設中心影響區與一般影響區交接處B點為坐標原點,那么,可以得到設中心影響區與一般影響區交接處A點坐標為(-d,0),AB兩點之間的距離為斷裂帶寬度,寬度大小為d。A′A段的撓度方程用式(6)表示:

y(x<-d)=y1=eφ1x(A1cosω1x+A2sinω1x)+

e-φ1x(A3cosω1x+A4sinω1x)

(6)

其中,φ1,ω1均為A′A段的彈性特征系數;A1,A2,A3,A4均為待定系數,此方程滿足無窮遠處的邊界條件:x→-∞,y→0。

故A3=0,A4=0,則有式(7):

y1=eφ1x(A1cosω1x+A2sinω1x)

(7)

同理,BB′段有式(8):

y(x>0)=y3=e-φ3x(A11cosω3x+A12sinω3x)-Dy

(8)

其中,φ3,ω3均為BB′段的彈性特征系數。AB段為中心影響區,其撓度方程式為式(9):

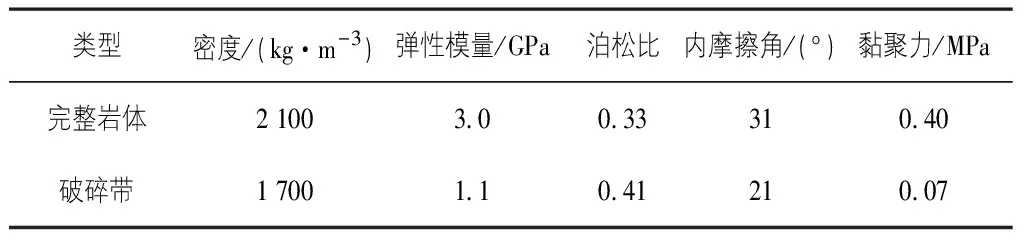
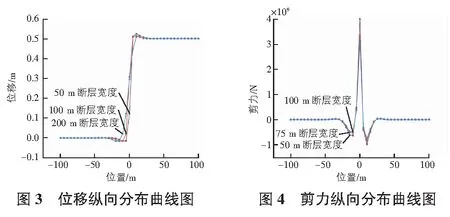
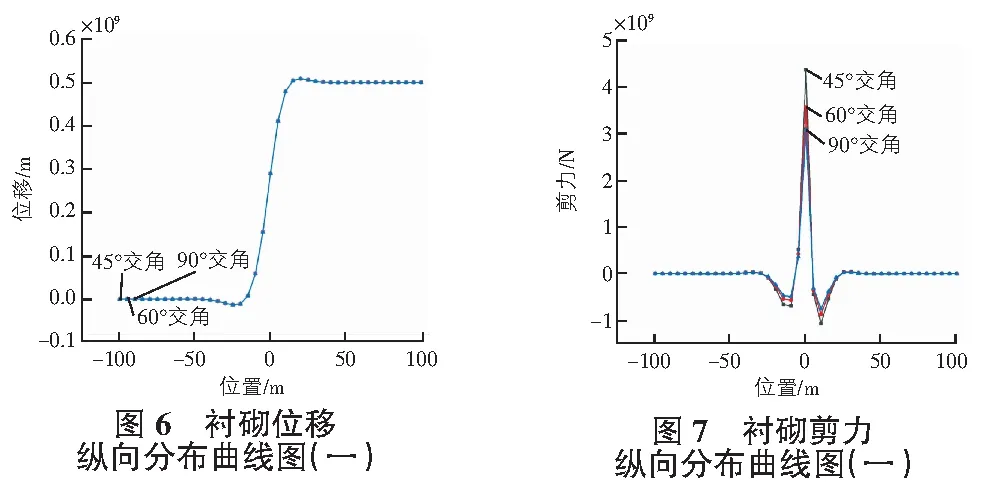
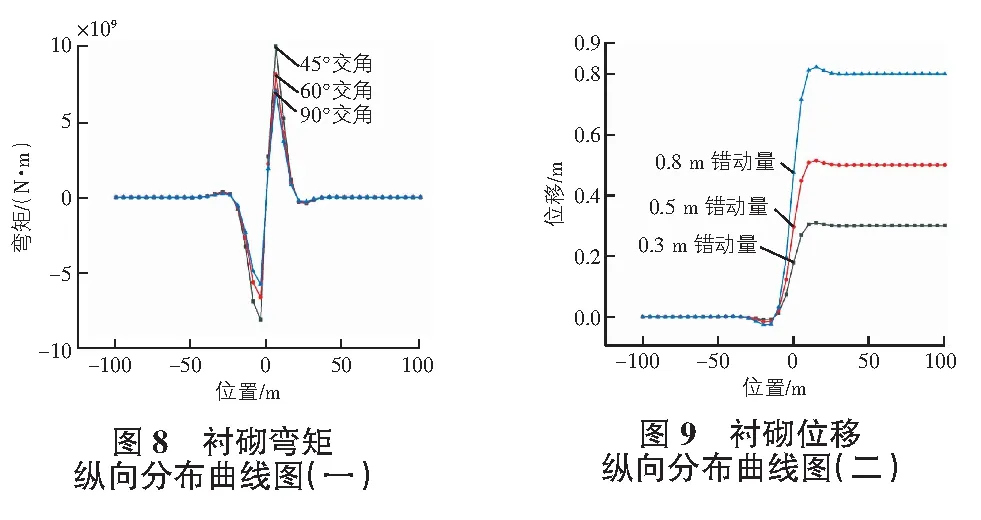
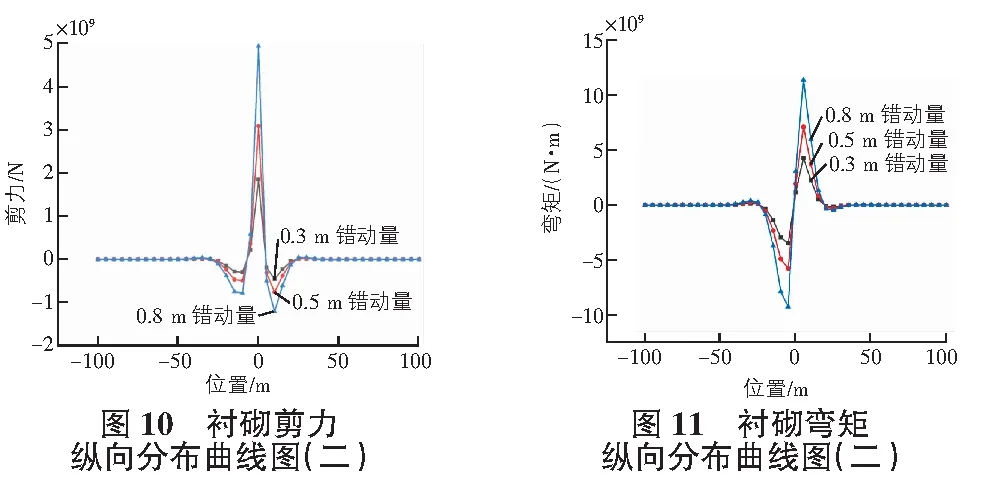
y(-d

e-φ2x(A7cosω2x+A8sinω2x)

(9)

對式(7)—式(9)整理,可得隧道縱向撓曲線方程為式(10):

(10)

其中,A5,A6,A7,A8,A11,A12均為待定系數。在A,B處,隧道的撓度、轉角、彎矩、剪力滿足連續性要求,因此式(11)滿足以下連續性條件,A處有式(11):

(11)

B處有式(12):

(12)

根據式(11),式(12),聯立求解方程組即可解得式(10)中的待定系數,得到隧道的撓曲線方程。為了得到隧道的轉角、彎矩和剪力,可進一步對撓曲線方程求導得出如下關于轉角、彎矩、剪力的表達式如式(13)—式(15)所示:

(13)

(14)

(15)

為了求得隧道縱向響應解析解,利用MATLAB計算程序,可編寫出關于以上方程組的求解程序,代入數值即可得出計算結果。

2.2 模型參數取值方法

地基系數k與圍巖的彈性模量、隧道的抗彎剛度等有關,可采用Vesic[10]提出的方法(式(16))進行計算:

(16)

垂直剪切模量G與圍巖的巖性和隧道埋深有關,可采用Tanahashi[11]經驗式(17)計算:

(17)

其中,ES,vS分別為巖彈性模量,N/m2,圍巖泊松比;H為隧道埋深,m。

注:本文所研究的斷層類型為走滑斷層,因此不考慮垂直剪切模量G的影響。

3 穿越斷層隧道圍巖-襯砌體系錯斷響應分析

以某實際公路工程為背景,隧道在近出口處穿越活動斷層,該活動斷層表現為右旋走滑型。本節主要研究的是在斷層錯動下隧道結構的受力響應,選擇對穿越隧道的二次襯砌的受力狀態進行分析。

3.1 不同斷層破碎帶寬度下斷層錯動對隧道結構的影響

在本研究中,選擇斷層隧道交角為90°,斷層錯動量為0.5 m不變,斷層破碎帶設置三種不同的計算工況,寬度分別設置為50 m,75 m,100 m。結合工程實際,材料物理力學參數值如表1,表2所示。

表1 巖體力學參數

表2 支護結構力學參數

通過計算繪圖,可以得到圖3—圖5所示的相關曲線圖。

圖3—圖5展示了不同斷層破碎帶寬度下襯砌位移及內力沿隧道縱向的分布曲線。從圖中可以看出,不同斷層破碎帶寬度對應的襯砌位移曲線沿隧道縱向的分布規律基本一致,不影響隧道結構最終位移大小,只對位移沿隧道縱向的分布范圍有少許影響,從內力分布曲線圖中可以看出,不同破碎帶寬度對應的襯砌內力曲線沿隧道縱向分布規律基本一致,斷層寬度大的對應的內力峰值較小。

3.2 不同斷層交角下斷層錯動對隧道結構的影響

考慮錯動量、斷層破碎帶寬度為定值,選取三種不同的斷層交角作為計算工況。選取100 m寬的斷層破碎帶,錯動量為0.5 m,斷層交角分別為45°,60°和90°三種工況,其他物理力學參數不變。通過計算可以繪制出圖6—圖8所示相關曲線圖。

根據圖6—圖8中的不同斷層交角下襯砌位移、內力沿隧道縱向分布曲線圖,不考慮沿隧道縱向內力和位移的分量,垂直隧道縱向的位移分量大小,不同斷層交角下襯砌位移最終相同,其內力峰值也隨斷層交角發生變化,剪力和彎矩的變化規律主要體現在影響范圍和峰值方面,從圖中可以看出,不同角度條件下,剪力和彎矩的影響范圍基本一致,但由于角度不同導致的錯動分量不同,斷層交角越小,其產生的剪力和彎矩的峰值越大。

3.3 不同斷層錯動量下斷層錯動對隧道結構的影響

為了研究在不同的斷層錯動量下隧道的內力分布,分別設置下盤的錯動量為0.3 m,0.5 m,0.8 m。破碎帶的寬度為100 m,斷層交角為90°,其他物理力學參數不變。通過計算結果繪制圖9—圖11的曲線圖。

通過圖9—圖11不同斷層錯動量下襯砌位移、內力沿隧道縱向分布曲線圖,其位移及內力沿隧道軸向分布符合一般規律。隨著錯動量的增大,隧道結構最大位移,剪力和彎矩的峰值都逐漸增大。

4 結論

對比分析隧道襯砌結構響應在不同工況下解析計算結果,隧道沿縱向的位移,彎矩和剪力分布規律與正逆斷層錯動規律相同,從而證明Pasternak雙參數彈性地基梁理論在走滑斷層中依然適用。通過不同條件下的錯斷響應分析,可以得出以下幾點結論:

1)斷層面兩側發生錯動的巖塊受錯動影響之后,受力變形主要集中在斷層面兩側的范圍內,斷層兩側的巖塊位移連續則出現在中心剪切帶位置。

2)發生斷層錯動時,襯砌急劇變形的范圍主要集中在斷層錯動面兩側的中心影響區范圍內;襯砌位移在斷層面兩側巖塊的交接處連續,斷層的左右盤對襯砌施加一組相反的彎矩,受力變形均勻。

3)在斷層錯動量、斷層隧道交角、斷層破碎帶寬度等不同參數作用下對隧道結構變形、內力分布及損傷規律均有一定的影響。對隧道結構影響最小的穿越角度為90°,斷層破碎帶寬度不同時,會對斷層錯動作用的影響范圍和襯砌內力峰值產生影響,斷層錯動量越大對隧道結構內力和位移影響越大,隧道受到斷層錯動作用越顯著。