趨勢分析法在監測網穩定性分析中的應用

謝朋朋，王 娟

(中國能源建設集團江蘇省電力設計院有限公司,江蘇 南京 211102)

0 引言

目前,對于控制網穩定性分析的常用方法主要有平均間隙法、t檢驗法和限差分析法等[1]。平均間隙法是一種整體性檢驗方法,其理論嚴密,但為找出網中的不穩定點需結合分塊間隙法同時進行,若點位較多時計算量較大,同時,由于目前大部分的平差軟件在平差過程中并不提供平均間隙法所必須的未知數的協因數陣,這就需要測量工作中花費大量時間解算協因數陣。t檢驗法的計算過程同樣需要計算協因數陣,因此,計算量較大,效率相對較低。限差分析法計算過程相對簡單,在工程上有一定的適用性,但該方法更多的需要依靠工程經驗來確定某一限差值。因此,本文結合具體工程實例,研究了一種基于建模分析理論即趨勢分析法在控制網穩定性分析中的可行性,并提出了一種建立判斷閾值的方法。

1 基于分形理論的趨勢分析法

1.1 基本原理

趨勢分析法是在總結事物客觀發展規律的基礎上,對考察對象的既有狀態或未來發展趨勢進行科學有效的判斷與預測。該方法通過分析歷史數據的發展趨勢,深層次把握研究對象的活動規律,通過建立模型預測研究對象的未來變化趨勢。目前,趨勢分析法已經廣泛應用于審計、醫療、軍事等多個領域。當把該方法應用于測量專業時,趨勢分析法表示的是一種建立在多期觀測數據基礎之上的建模分析方法[2],據此,可以嘗試將趨勢分析法應用到控制網的穩定性分析中去。使用趨勢分析法進行控制網穩定性分析的基本原理是根據以往多期觀測數據模擬出控制網中某一點位的變化趨勢,當趨勢模擬值與實測值之間的差值超過某一設定閾值時,認為該點在兩期測量期間發生了移動,反之,則認為該點處于穩定狀態。以建立線性模型為例,當模擬值與實測值的關系如圖1左圖所示時,表示該點位處于穩定狀態;當模擬值與實測值的關系如圖1右圖所示時,則表明該點位在兩期測量期間發生了位移。

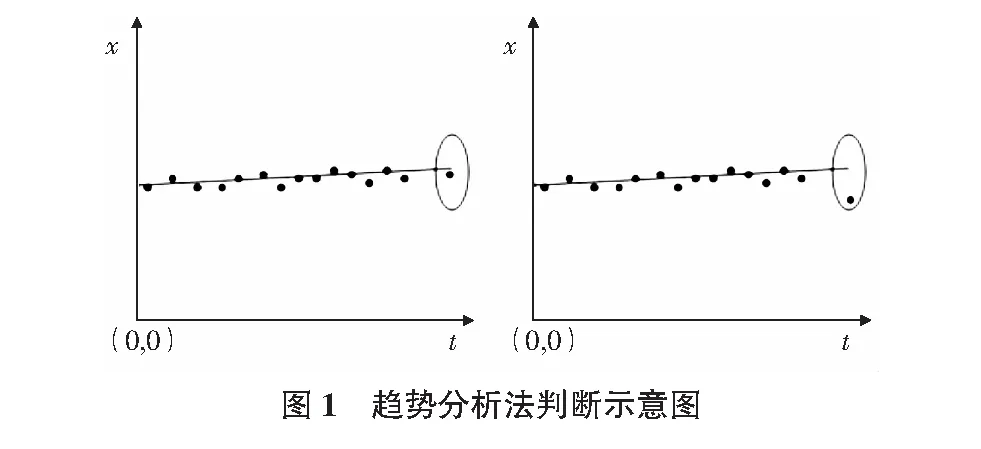
趨勢分析法在控制網穩定性分析中的判斷精度主要與建模方法和閾值有關,目前常用的建模方法主要有線性回歸法、灰色模型、神經網絡、分形理論等等。本部分將結合分形理論對趨勢分析法在控制網穩定性分析中的應用進行研究。

分形理論誕生于20世紀70年代,其是基于部分與整體之間的相似性直接從研究對象的本身出發來研究系統自身的固有規律,它可以揭示深藏在系統中看似毫無規則的組織形式[3]。自誕生以來,尤其是20世紀90年代后,分形理論開始在很多不同領域得到了成功的應用。

分形理論可以使用冪指數分布來表示:

(1)

進一步推算得到:

(2)

其中,r為系統特征線度,如時間;N為與r有關的相關物理量;C為某一特定常數;D為維數,即反映組織結構的量。分形理論根據分維形式的不同可以分為常維分形和變維分形兩種常用的模型[4]。

1)常維分形。顧名思義,常維分形指的是分形維數D為常數的分形模式,該模型在雙對數坐標系中表現為一條直線。在此情況下,系統中只需存在兩組有效數據(Ni,ri),(Nj,rj),由式(1),式(2)便可計算得到分形維數D和常數C的值見式(3),式(4):

(3)

C=NirD

(4)

需要注意的是當N和r中存在負數時,上式將無法進行對數運算,面對這種情況只需將全部數據點加上一個特定的常數,即對所有數據點進行統一的平移變換便可達到消除所有負數的目的。

常維分形適用于維數D為固定常數的情形,當雙對數坐標系中出現了非線性的函數關系時,一種處理方法便是使用最小二乘方法求解出分形參數D,但是這樣求解得到的參數D會影響構造的模型精度。因此,面對這種情況時,通常會采用變維分形的方法來構造模型。

2)變維分形。變維分形,即在建模過程中分維參數D是線度r的函數,為不斷變化的量。

D=F(r)

(5)

則物理量N與線度r之間的函數關系可表示為:

(6)

因此,便可由此得到:

(7)

變維分形可以在很大程度上解決常維分形無法解決的一些問題,但相應的,其在構造模型方面也相對復雜。目前常用的變維分形建模方法主要為分段變維分形建模,該方法首先是將原始數據序列進行累加和處理,變換后的數據在雙對數坐標系中基本上符合直線的要求,此時便可利用常維分形的理論來進行處理,具體步驟如下[5]:

a.分別以ln(r)和ln(N)為橫坐標和縱坐標建立雙對數坐標系,將原始數據序列(Ni,ri)(i=1,2,…,n)對數變換后展繪到坐標系中,將Ni序列作為一個基本序列,即Ni=(N1,N2,…,Nn)。

b.根據基本序列不斷構造后續所需要的所有序列,如構造一階累加和序列S1,其中S11=N1,S12=N1+N2,S13=N1+N2+N3…,同理便可構造出二階、三階、n階累加和序列S2,S3,Sn,即:

{S1}={N1,N1+N2,N1+N2+N3…},

{S2}={S11,S11+S12,S11+S12+S13…},

{S3}={S21,S21+S22,S21+S22+S23…},

?

{Sn}={S(n-1)1,S(n-1)1+S(n-1)2,

S(n-1)1+S(n-1)2+S(n-1)3…}。

c.得到原始數據的各階累加和后,便可建立各階累加和的變維分形模型。以建立一階累加和的變維分形模型為例,將數據序列(S1i,ri)經對數變換后在雙對數坐標系中依次連接,從而得到各分段模型,分別使用常維分形方法計算各分段的分形參數。

d.使用插值法求出需要擬合的各分段的分形參數,最終得到需要的擬合點的數據。

1.2 閾值的確定

使用趨勢分析法進行控制網穩定性分析時,在得到趨勢值后,可以根據圖1所示的方法進行判斷。但是這種方法得到的結果只是根據經驗做出的直觀判斷,無法做到精確的定量分析。為了得到準確的判斷結果需要確定定量的判斷依據,即通過趨勢分析法擬合出各點的變化趨勢后,通過與實測值對比,當趨勢值與實測值的差值大于某一閾值時,便認為該點在兩期測量之間發生了明顯位移。因此,閾值的確定在很大程度上會影響最終的判斷結果。目前,尚未有相關文獻對該閾值的選取作過必要的研究,受到差分析法確定閾值方法的啟發,本文嘗試使用以下構造閾值的方法來進行穩定性分析的研究:

(8)

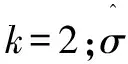
(9)

2 實例分析

本文選取某抽水蓄能電站水工外部結構平面監測網共10期的有效數據。為研究最新一期控制網點的穩定性情況,以前9期為原始數據序列建立模型。以點位LE5的穩定性檢驗為例,說明具體情況,首先進行X坐標分量的穩定性檢驗,各期監測數據及各分段分維值見表1。

表1 LE5點X分量實測值及各段分形維數

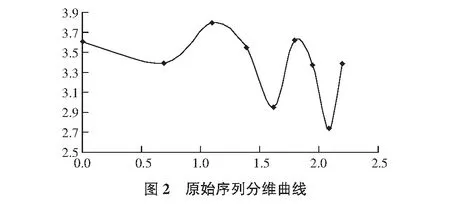
以lnN,lnr分別為縱橫坐標建立雙對數坐標系,將序列(Ni,ri)經對數轉換并對Ni列數據進行平移放大后展繪于坐標系中,見圖2。

從圖2可以直觀地看出原始序列的分維曲線是一條無規則的曲線,且表1中的分維值D有正有負,因此在使用分形理論進行建模時,應使用變維分形方法。將原始序列進行一階累加處理,并計算相應各段分維數,見表2。

表2 LE5點X分量實測值一階累加及各段分形維數

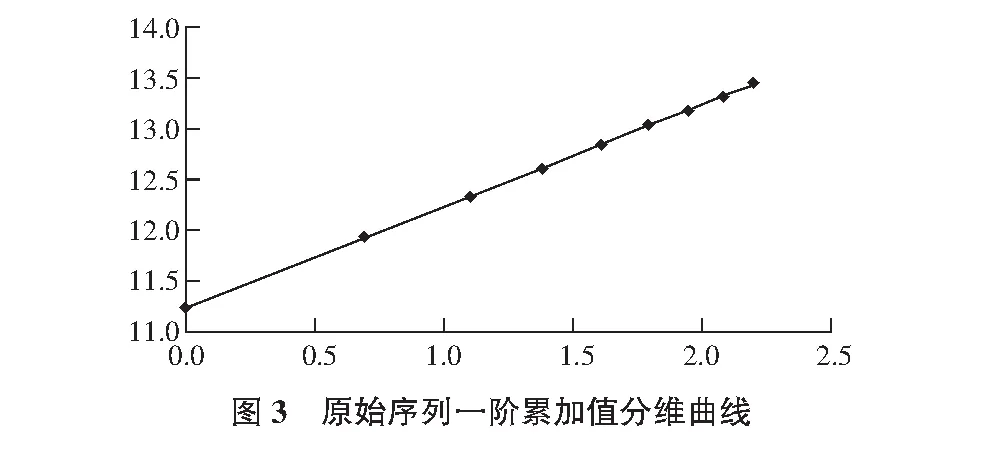
同樣,以lnS1,lnr分別為縱橫坐標建立雙對數坐標系,將序列(S1i,ri)經對數轉換后展繪于坐標系中,見圖3。

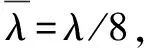
接下來,按照上述步驟繼續對點位LE5的Y坐標分量進行穩定性檢驗,得到Y坐標分量第10期的位移趨勢量為Y0=19 144.274 5 m。

按照上述步驟,依次計算得到控制網中9個點位的第10期位移趨勢量,具體見表3。

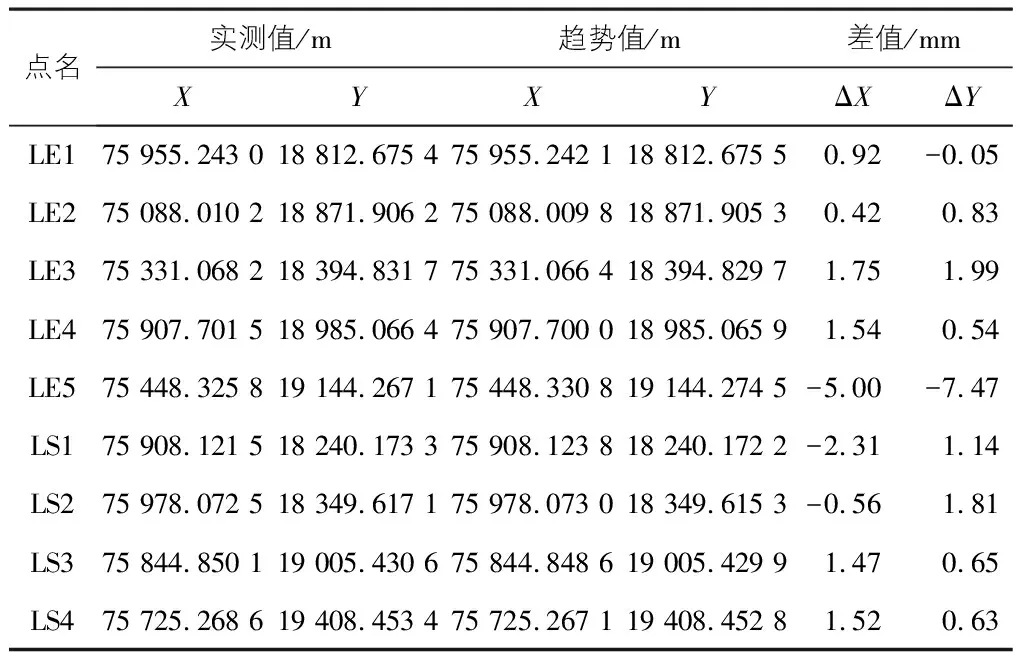
表3 各點位趨勢值

分別使用平均間隙法、t檢驗法和基于分形理論的趨勢分析法對本工程平面監測控制網進行穩定性分析[6-7],現將三種方法得到的結果進行比較分析。

從表4可以看出三種方法得到的結論一致,由此也驗證了文中提出的閾值確定方法的準確性,也說明了基于分形理論的趨勢分析法可以應用到本工程變形監測控制網穩定性分析中去。

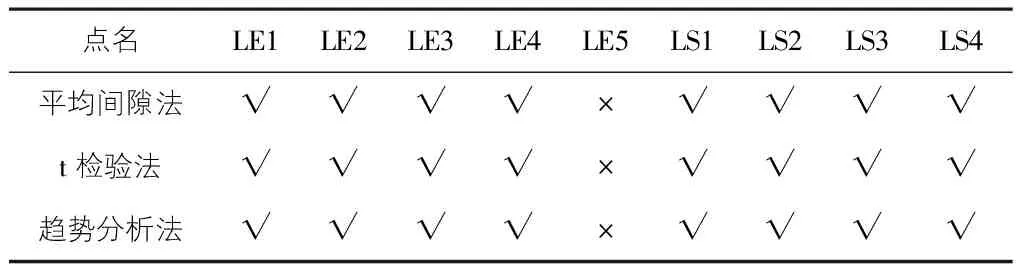
表4 平面監測網穩定性分析結果

3 結語

變形監測控制網是整個變形監測的基礎,因此,對于變形監測控制網的穩定性分析極其重要。本文結合某抽水蓄能電站平面監測控制網穩定性分析實例,進行了基于分形理論的趨勢分析法在控制網穩定性分析的實驗驗證,并將分析結果與平均間隙法和t檢驗法的結果進行對比分析,驗證了文中所提閾值確定方法的準確性。同時,也說明利用基于分形理論的趨勢分析法進行變形監測控制網穩定性分析在本工程中是可行的。