基于改進K-means聚類算法與馬爾可夫鏈的風機性能評估新方法

文孝強 楊剴勛 許子昂

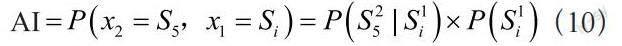
摘? 要：為解決常規風功率曲線法對風機發電性能評估時，因數據刪除過多造成發電性能評估不準確的問題，提出一種基于改進K-means聚類算法與馬爾可夫鏈的風機性能評估新方法。首先，使用改進的K-means方法對風機輸出功率-風速散點圖進行工況劃分；其次，通過對比實驗確定最佳聚類中心數目，使用馬爾可夫鏈針對聚類后的數據建立狀態轉移矩陣，求出風機異常指數，據此分析引起風電機組發電效率下降的根源。應用實例表明，所提出的方法能夠對運行風機的發電性能進行有效分析，可為風機發電效率的提升提供重要的理論參考。

關鍵詞：風機；發電性能；評估

中圖分類號：TP39；TM315 文獻標識碼：A 文章編號：2096-4706（2023）17-0066-05

A New Method for Evaluating Wind Turbine Performance Based on

Improved K-means Clustering Algorithm and Markov Chain

WEN Xiaoqiang1， YANG Kaixun2， XU Ziang1

（1.School of Automation Engineering， Northeast Electric Power University， Jilin? 132012， China;

2.School of Information and Control Engineering， Jilin Institute of Chemical Technology， Jilin? 132012， China）

Abstract： In order to solve the problem of inaccurate power generation performance evaluation due to excessive data deletion when evaluating the power generation performance of Wind Turbines （WT） by conventional wind power curve method， a new method for wind turbine performance evaluation based on improved K-means clustering algorithm and Markov chain is proposed. Firstly， the improved K-means method is used to divide the working conditions of the WT output power-wind speed scatter plot. Then， the optimal number of clustering centers is determined by comparative experiments， and the state transition matrix is established by using Markov chain for the clustered data. The anomaly index of the WT is obtained， and the root cause of the decrease in the power generation efficiency of the WT is analyzed. Application examples show that the proposed method can effectively analyze the power generation performance of the operating WT， which provides an important theoretical reference for the improvement of the power generation efficiency of the WT.

Keywords： wind turbine; power generation performance; assessment

0? 引? 言

為了更好地獲取風能，風機通常都會安裝在較為偏遠的地區。然而，這些地區環境較為惡劣，天氣復雜多變，風電機組實際性能要低于額定指標，從而導致風機發電效率降低。鑒于此，利用風機運行過程中產生的SCADA數據，對風機當前發電性能與狀態進行評估，深入分析導致發電性能下降的因素，并提出有針對性的建議，對風電場的經濟效益提升和風機平穩運行有重要意義。文獻[1]通過灰色關聯度對風機SCADA數據進行分析，求取各參數之間的相關性后建立了風機健康性能評估模型，并求出了性能退化曲線。文獻[2]提出基于高斯過程回歸與指數加權移動平均窗口的風電機組發電性能評估模型。首先使用偏最小二乘法計算SCADA數據中與功率相關的變量作為模型輸入，接著使用高斯過程建立理論風功率曲線模型并與實際風功率曲線求取殘差后進行處理分析，結果表明該方法能有效地對發電性能下降與劣化進行評估。文獻[3]提出了基于改進高斯回歸的風功率曲線模型，將影響風并電機組發電的因素作為模型自變量，使用Cholesky分解對高斯方法進行改進并建立風功率曲線模型，結果表明該方法建模精度提高，能更好地分析風機發電性能。文獻[4]建立了一種不確定性風功率曲線模型，使用相關向量機求出功率置信區間，基于此對風機關鍵部位的故障進行了有效的監測與預警。文獻[5]通過對現場SCADA數據進行分析，得到對風電機組發電效率影響較高的參數，使用處理后的數據建立風功率曲線模型，并對比分析了兩個機組年發電量存在差異化的原因，等等。風功率曲線能直接反映風機發電性能的好壞，但目前使用風功率曲線時，往往需要刪除大量數據。致使這些實際上包含大量有用信息的數據，在處理過程中往往被人為清洗掉了。本文以此為切入點，以原始風功率曲線為研究對象，通過聚類劃分出風機發電性能正常與低下的工況，并對聚類后的數據使用馬爾可夫鏈進行性能評估，給出運維建議。

1? 風機發電性能評估算法基本流程

首先對風功率曲線進行工況劃分。如果一臺風機處于健康狀態，那么功率會隨風速的增加而增加。但是一旦風機出現故障，那么即使風速較高功率也不會上升，因此將運行風機工況劃分成正常與低效兩種狀態。接下來對風機運行進行分析。在此使用馬爾可夫鏈建立風機狀態轉移矩陣。具體評估流程如下：

1）首先建立剔除記錄錯誤的數據。本文以某風場2號風機作為研究對象，采集了該風機2017年8—10月與2018年2—3月的數據。

2）由于所采用的風功率數據較為分散，會存在部分散點。若采用K-means算法確定聚類中心，由于K-means算法受到這些散點的影響，使得結果與實際情況會存在一定偏差。為了避免這一情況的出現，本文使用了一種改進的K-means算法進行工況劃分，以確定聚類中心個數。

3）對劃分后的工況數據使用馬爾可夫鏈建立狀態轉移矩陣。以時間序列為輸入，求初始轉移概率，得到當前狀態轉移到下一狀態的概率，最終得到風機異常指標。根據這一結果給出運維建議，從而減少故障發生，提高風機發電效率。

2? 風功率數據工況劃分與分析

2.1? 聚類中心的劃分

風功率直接反映風機發電效率高低，根據文獻[6]可知，建立風功率曲線時往往需要刪除大量數據。這些被刪除的點往往是相同風速下功率較低的點，這些點大多處于高風速，但功率卻較低，事實上，這些被刪除的數據可能包含有用的信息。因此有必要將這些點作為功率低下的點，以挖掘其中有用的信息。圖1為刪除風速下功率較低的點前后的對比圖。可見這種預處理方法會刪除數據中可能有用的信息。它們也會反映出風機的運行狀態等信息，通過挖掘并分析可以得到風機運維的建議，對提升風機發電性能有一定幫助。另外，原始風功率數據中確實會記錄一些錯誤的數據，例如停機后仍記錄的數據，傳感器異常數據等離群點。這些離群點會影響工況的劃分，因此我們在進行工況劃分時需要剔除這些離群點。因此，本文在原始風功率曲線的基礎上只剔除錯誤數據，保留大部分數據的同時也保留了數據的信息。只刪除部分離群點所得功率散點如圖1（b）所示。

（a）平滑處理后風功率散點圖

（b）本文刪除離群點后風功率散點圖

接下來對數據進行標準化處理，標準化公式為：

其中，μx表示特征的平均值，δx表示特征的標準差。

聚類算法屬于數據挖掘的一種方式，在數據挖掘領域中占據了重要地位[7]。聚類是一種無監督的學習方式，不需要標簽。本文針對常規K-means算法[8]所存在的不足，提出一種改進的K-means算法，具體流程如下：

1）構建數據集X = {x1， x2， …， xn}，從所有的數據點中選出密度最大的一個點，稱為初始聚類中心點p1。

2）計算數據集中其他點與p1的距離最遠的點，作為第二個聚類中心p2：

3）選擇max （d （ p1，xn） + d （ p2，xn））作為第三個聚類中心p3。

4）第k個聚類中心則為 。

采用該聚類算法，將2號風機2017年8—10月數據劃分為4類的結果，如圖2（a）所示。由圖可知，聚類結果在三個簇的交點處有些正常功率點被劃分為功率低下點，圖中圓圈處的部分數據屬于正常發電狀態，卻將其聚類為低效發電狀態，不符合實際，因此需要調整聚類數目，由原來的4類調整為5類，調整后的結果如圖2（b）所示。與圖2（a）相比，調整聚類中心后能有效地將正常功率點與功率低下點區分開，其中編號為5的類為低效發電狀態，其余4類為正常發電狀態。

2.2? 工況分析

2號風機故障時刻表如表1所示，對發電性能的分析如下：以2017年9月25日1～22點風速與功率為例，在1～13點期間風速在4～8 m/s之間，在上午3點附近風速較低在4 m/s附近，風機功率在100 kW/h左右，在工況1狀態；持續到上午11點左右，風速上升到8 m/s附近，功率上升到300 kW/h附近，處于工況2狀態；在14點左右風速上升到10 m/s，但風機功率沒有明顯增加，持續到22點風速很高但功率均未達到1 000 kW/h以上，處于工況5狀態；從表中可以看出在15點與18點左右風機槳葉頻繁報警，導致報警前后一段時間內風機的功率受到很大影響，不會隨風速增加而增加，發電性能受到很大影響。

3? 實驗驗證

3.1? 馬爾可夫模型

為了對發電性能進行評估，本文使用馬爾可夫鏈建立風機狀態轉移矩陣。假設狀態轉移矩陣為R，初始條件概率為I，狀態空間為S，得到：

其中，pij = P（Sj | Si），qi = P（Si），從而得到馬爾可夫無記憶公式：

風機狀態轉移到工況5時稱作異常指數AI：

其中，上標k表示在時間序列中所在的位置，下標i表示時間序列數據所處的狀態。對異常指數AI進行證明：

任意一條路徑可按式（8）表示：

馬爾可夫模型當前狀態不會記憶上一時刻，因此式（8）可以簡化為：

其中， 表示狀態Sn與上一狀態Sn-1的轉移概率， 表示初始狀態的概率，由上述公式可知，異常指數可以跨越多個狀態定義。

3.2? 狀態轉移矩陣

根據2.2中結果，并結合3.1模型，建立風機狀態轉移矩陣，2號風機2017年8—10月狀態轉移矩陣如表2所示。其中，縱向代表當前狀態，橫向代表下一時刻狀態，數值為狀態轉移概率。狀態5對應發電性能低效狀態。當風機從其他狀態轉移到狀態5時，風機發電效率會降低。可見3狀態轉移到5狀態概率最高。在8—10月期間，該風機槳葉變頻故障與變槳故障發生次數最多，占到總故障的70%左右。對角線上的概率為狀態的穩定性。可以看出，主對角線上的概率相較于非對角線的概率高出很多，說明風機運行狀態較為穩定，狀態5自身轉換的概率為0.728 7，說明風機進入狀態5會持續較長時間，而不是很快轉移到其他正常狀態。采用同樣的方法，對2號風機2—3月計算狀態轉移矩陣，結果如表3所示。

表3中3狀態轉移到5狀態概率最高。在2018年2—3月期間，該風機偏航系統故障、風向儀與風向角偏差過大故障發生次數最多，占到總故障的75%左右。從表3中可以看出，主對角線上的概率相較于非對角線的概率高出很多，說明風機運行狀態比較穩定，狀態5自身轉換的概率為0.836 8，說明進入狀態5同樣會持續很長時間，并且相比于該風機2017年8—10月持續時間更長。

根據以上分析可知：當風機從正常發電工況轉移到低效發電工況時，也就是從當前工況1、2、3、4狀態轉移到工況5，風機多已處于故障狀態，發電性能較低，此時將其定義為異常指數AI（Anomaly indicators）。通過分析異常指數AI可以為風場運維人員提供決策依據。結合實際數據與以上公式，AI定義為：

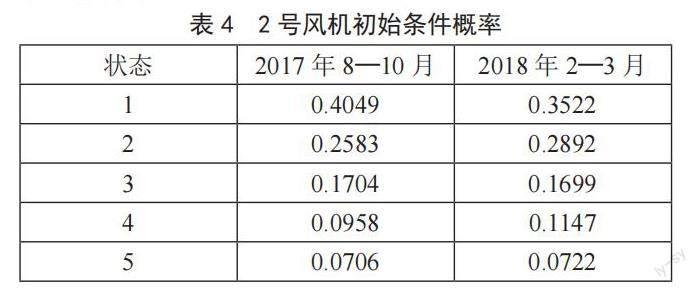
其中，i = 1，2，3，4。則2號風機初始概率如表4所示。

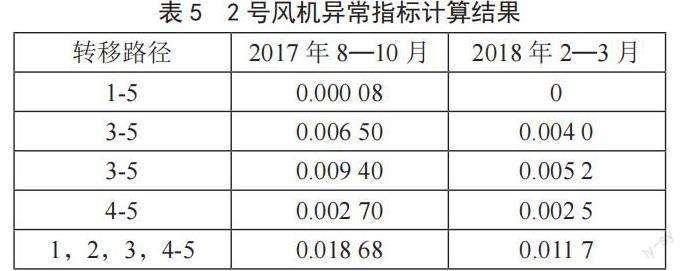
風機初始條件概率為起始時刻風機所處的狀態，從表4中可以看出，狀態1、2、3的起始概率較高，對應風速在0～8 m/s，因此很少轉移到狀態5。2號風機異常指標、風機故障與維修次數如表5、6所示。由表5可知，風機在2017年8—10月異常指數要略微高于2018年2—3月。與自身相比，風機經過一段時間后的異常指數有所降低。對比風機在8—10月與2—3月兩個階段的運行狀況，可知風機從狀態3轉移到狀態5的概率要明顯高于其余狀態。結合風機維修記錄可知，風機在此期間槳葉故障與偏航系統故障較多，因此對于提高2號風機的發電性能，需要進行定期檢修與更換器件，尤其是槳葉與偏航系統，檢修頻率應在6個月左右。

4? 結? 論

對K-means算法進行了改進，在選取初始聚類中心時進行人為干預，通過密度方法進行聚類中心選取，結果表明該方法可以有效地區分出風機工況。

對聚類中心個數進行討論。首先當聚類中心為4時，結果表明有部分數據劃分與實際情況不符，調整為5后，結果與實際相符。

使用馬爾可夫鏈建立了風機狀態轉移矩陣并求出異常指數。通過異常指數可以看出，為提高2號風機的發電性能，需要進行定期檢修與更換器件，尤其是槳葉與偏航系統，檢修頻率應在控制在6個月左右。

參考文獻：

[1] 郭雙全.基于灰色關聯度的風力發電機組健康性能評估方法研究 [J].裝備機械，2016（1）：7-11.

[2] 馬東，孔德同，郭鵬，等.基于SCADA運行數據的風電機組發電性能劣化監測研究 [J].可再生能源，2021，39（1）：45-49.

[3] 郭鵬，劉琳.多變量風電機組功率曲線建模與監測研究 [J].電網技術，2018，42（10）：3347-3354.

[4] 張方紅，荊博，錢政，等.基于相關向量機的風電機組功率曲線建模與監測 [J].船舶工程，2020，42（S2）：171-174+191.

[5] WANG P C，ZHANG Y P，YUAN S，et al. Analysis and application of the relationship between wind power curve and power generation based on operating data [J/OL].Journal of Physics： Conference Series，2020，1676（1）：1-5[2023-02-07].https：//iopscience.iop.org/article/10.1088/1742-6596/1676/1/012205.

[6] BENNOUNA O，H?RAUD N，CAMBLONG H. Diagnosis and fault signature analysis of a wind turbine at a variable speed [J].Proceedings of the Institution of Mechanical Engineers： Part O.Journal of Risk and Reliability，2009，223（1）：41-50.

[7] JAIN A K. Statistical pattern recognition： a review [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（1）：4-37.

[8] 孫士保，秦克云.改進的k-平均聚類算法研究 [J].計算機工程，2007（13）：200-201+209.

作者簡介：文孝強（1979—），男，漢族，山東莒南人，副教授，博士，研究方向：風機健康狀態管理與評估。