基于探地雷達功率譜屬性參數的土壤含水狀態預測

謝國青，聶俊麗，陳紫秋，熊悅意，馮艷玲，陳德文

（1.貴州大學國土資源部喀斯特環境與地質災害重點實驗室，貴陽 550025；2.貴州大學資源與環境工程學院，貴陽 550025）

0 引 言

土壤含水率(SWC)是表征土壤水分狀況、反映土體組成的重要指標，準確測定土壤含水量在土木工程、農業生產和生態修復方面發揮著關鍵作用[1,2]。常規的土壤含水率測量方法需要對土層進行鉆孔取樣，該方法測量結果雖然直觀準確，但容易破壞土層結構完整性且采樣費時費力。因此，研究一種無損快速準確探測土壤含水構造的方法，對農業生產、生態環境保護等具有重要意義。探地雷達(GPR)是一種通過高頻電磁波推測地質體空間結構和物性參數的地球物理方法，具有無損、快速、探測精度高等優點，近年來，已被廣泛應用于中尺度范圍內土壤含水率的探測研究中[3-5]。現有的探地雷達探測土壤含水率的方法多利用信號時域屬性，通過時域信號估算土壤介電常數并建立相應的關系模型來估算土壤含水率，具有原理簡單易于實現的優點，但時域方法反演含水率精度受到反演得到的介電常數及相關關系模型的影響，容易產生誤差的二次傳遞[6]。近年來，越來越多的學者開始研究基于雷達信號頻域功率譜估計土壤含水率的方法。楊峰首次將功率譜方法引入路基含水率計算中，提出利用路基材質與水介質對應的功率譜面域能量比值經驗公式進行含水率求取與路基富水病害判別。通過雷達檢測頻譜分析結果與現場取樣試驗室分析結果對比，歸納總結出對應于模型的雷達波峰譜面域與不同介質元素的峰譜面域構成比例關系[7]。聶俊麗基于ARMA 功率譜估計方法，成功的反演了風積沙地區的砂壤含水率[8]。張浩浩采用ARMA 功率譜分析方法，通過物理實驗研究了不同路基病害的雷達信號頻譜響應特征，并基于雷達信號響應特征成功地對模型路基富水病害進行了識別[9]。鄭龍金針對地下富水異常體探測提出利用功率譜能量統計值與滾動功率譜結合的方法判別富水區域分布情況，并利用譜面域經驗公式對富水體含水率進行計算[10]。崔凡等人提出了對功率譜頻帶進行劃分，選擇了一個頻率分界點，計算低頻疊加與整個頻譜能量的比值，并建立該值與實測土壤含水率的關系模型，隨后使用關系模型成功地反演了0～10 m 砂壤的含水率[11]。前人在利用功率譜方法反演土壤含水率的研究中，僅考慮功率譜單一屬性與土壤含水率的關系，并未對功率譜屬性進行全面研究，主要方法為通過建立功率譜能量或頻域屬性與土壤含水率之間的關系模型進行含水率探測。為此，本文在前人對功率譜屬性研究基礎上，采用屬性分析方法提取功率譜多種屬性參數，并基于物理模型探地雷達數據，利用探地雷達功率譜屬性參數和BP 神經網絡相結合的方法對土壤含水率進行預測，以期達到快速準確計算土壤含水率的目的。

1 材料與方法

1.1 物理實驗

建立了長寬高分別為1.8、1.0、0.8 m 的不同含水率物理模型，采用5 mm 篩網對土壤進行細篩，使用主頻天線為400 MHz 探地雷達對模型4 個采樣點進行點測，采樣時窗為30 ns，采樣點數為1 024。測完后從模型由上至下每間隔10 cm 進行環刀取樣，每層在雷達點測處取樣，連續取得8個不同深度的土壤樣本。一次探測結束后使用攪拌機對土樣進行攪拌，每次噴灑相同體積水，攪拌半小時后裝入模型靜置12 h 后進行探測，共采集了8組不同含水率土壤模型，最后將采集到的土壤樣本帶回實驗室。按照規范《LY/T 1213-1999 森林土壤含水量的測定》的要求，采用烘干法測量樣本土壤含水率以及土壤容重等參數，其模型平均含水率見表1。

表1 實測模型含水率Tab.1 The measured water content of the model

1.2 野外實驗

采樣區域位于貴陽市貴州大學(106°39'19″E，26°26'55″N)，采樣點一位于貴州大學物探試驗場內，地表植被裸露，地表潮濕土壤含水率較高；采樣點二位于貴州大學野外空地，地表覆蓋植被，且表層含有薄薄一層腐殖質，為提高探測效果，對探測區域進行了整理，鏟除地表植被與累積的腐殖質。首先使用400 MHz天線進行點測，采樣時窗為35 ns，采樣點數為1 024；然后在測點中間自上而下每隔10 cm 取一個樣，取樣深度為0.8 m。

1.3 功率譜方法原理及屬性提取

假定離散信號x(n)是由一個輸入序列u(n)通過一個線性時不變系統H(z)輸出所得，通過已知x(n)及其自相關函數rx(m)來估計線性系統H(z)的參數，最后利用H(z)的參數求解信號x(n)功率譜的方法稱為現代功率譜分析方法。

離散隨機信號x(n)與白噪聲方差為σ2的隨機噪聲u(n)總有如下關系：

其中若b1,b2,…,bq全為零，則式(1)稱為自回歸(autoregressive,AR)模型，該模型表示當前輸出信號是由前p 個延遲信號和現在的輸入加權而成；若a1,a2,…,ap全為零，則式(1)稱為滑動平均(moving-average,MA)模型；若b1,b2,…,bq和a1,a2,…,ap不全為零時則稱式(1)為自回歸滑動平均(Auto-Regressive Moving Average Model)模型。其中由于AR 模型參數計算簡單，具有較高譜分辨能力，任意的MA 和ARMA 模型都可以由AR模型有限階推出，所以在功率譜估計中AR 模型應用較多[12]，因此本文選擇使用AR 模型作為探地雷達信號功率譜估計的方法。

當b1,b2,…,bq全為零時，式(1)可看作信號x(n)是由k 個隨機噪聲u(n)和線性隨機系統H(z)的關系式：

輸入信號u(n)與通過線性隨機系統H(z)后輸出的信號x(n)有如下關系：

由公式(2)～(5)，得x(n)的p階AR模型功率譜密度為：

從式(6)可看出當確定AR模型的參數a1,a2,…,ap，白噪聲方差σ2和AR 模型階數p 時，便可得到x(n)的功率譜，其中AR 模型的參數a1,a2,…,ap和白噪聲方差σ2可利用Yule-Walker 方程解出：

為實現利用功率譜屬性反演土壤含水率，本文在前人的研究基礎上從功率譜在頻域、能量、聚合程度和能量分布等4個特征屬性角度對雷達信號功率譜進行分析，提取雷達功率譜屬性共11種[13-16]，表2給出關于功率譜屬性的提取方法。

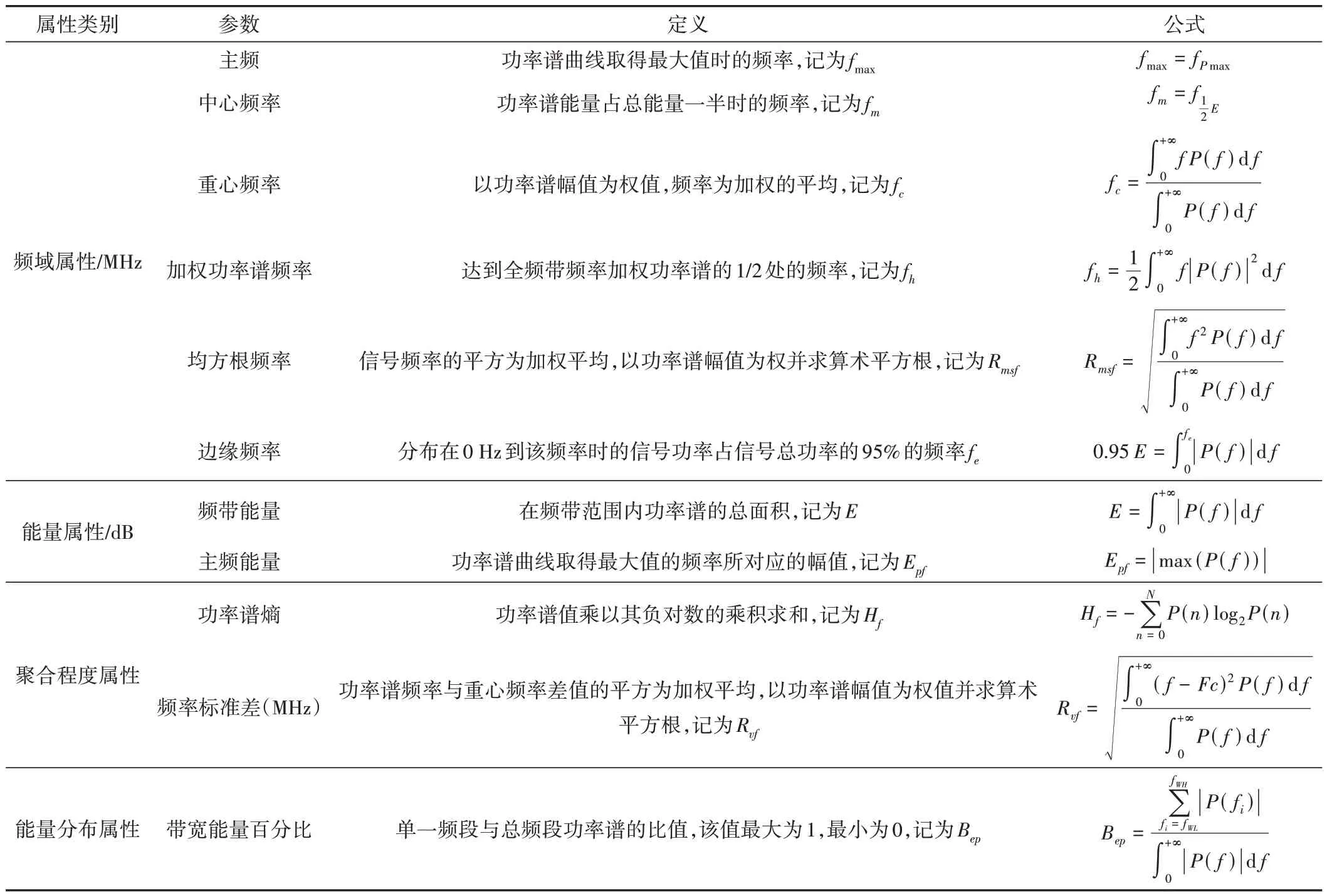
表2 功率譜參數屬性表Tab.2 Power spectral parameter attribute table

1.4 神經網絡預測模型構建方法

BP 神經網絡具有強大的學習、記憶、容錯、非線性和自適應能力，可通過反復學習大量數據實現輸入到輸出的映射，數學理論證明三層神經網絡可逼近任何非線性連續函數，使其特別適合于求解內部機制復雜的問題，即具有較強的非線性映射能力[17-19]。因此本文選擇BP 神經網絡方法對土壤含水狀態進行預測。BP 神經網絡主要分為輸入層、隱含層和輸出層，其中隱含層中每層的節點又稱為神經元，通過輸入層樣本在神經網絡中正向傳播得到輸出類別與預期輸出進行對比，將分類誤差不斷反向傳播改變隱含層神經元之間的連接權值，使得輸入樣本通過神經網絡的輸出與事實輸出一致。其算法流程如圖1所示，主要分為輸入數據預處理、網絡設計、正向傳播和誤差反向調整4個部分。

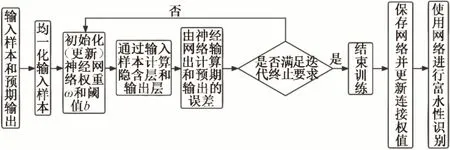
圖1 BP神經網絡預測算法流程圖Fig.1 Backpropagation neural network prediction algorithm flowchart

(1)確認輸入樣本數據及預期樣本輸出數據，并對輸入樣本數據做歸一化等預處理。

(2)設計神經網絡層數、神經元個數并初始化各層各神經元的權重和閾值。

(3)根據輸入層樣本數據確認隱藏層輸入數據，并根據隱含層激活函數計算隱藏層輸出。

(4)由隱含層輸出數據計算輸出層輸入數據，根據輸出層激活函數計算神經網絡實際輸出數據。

(5)依據實際輸出數據與期望輸出數據計算兩者之間的總誤差。

(6)將總誤差通過隱含層與輸出層之間的權重值傳遞并更新連接權重。

(7)將隱含層之間的誤差傳遞至輸入層與隱含層并更新連接權重。

通過設置迭代次數與精度，利用輸入樣本和預期輸出不斷更新輸出層、隱含層和輸出層之間的神經元連接權值直到迭代次數和誤差滿足精度要求后停止神經網絡學習，并保存更新后的權值，這便是一個完整的BP 網絡預測算法流程。將測試數據輸入神經網絡即可完成對輸入數據的輸出預測。

1.5 數據處理

物理實驗和野外實驗探地雷達數據預處理、雷達信號功率譜估計、功率譜屬性參數提取優化、BP 神經網絡模型建立及滾動時間窗剖面技術在MATLAB2020a 中通過編程實現，采用SPSS 22.0進行功率譜屬性和土壤含水率的Pearson 相關性分析，使用Origin 2020進行作圖。

2 結果與分析

2.1 物理實驗結果

在數據采集結束后，使用MATLAB 編寫的預處理程序進行零點校正、背景去噪以及濾波等處理。通過模型底部反射面確定實驗模型的雷達信號時窗范圍，并采用時窗選取壓縮變換技術截取模型范圍內的雷達信號，利用AR 功率譜法提取雷達雷達信號的功率譜(圖2)，并根據表2 提取探地雷達功率譜參數，計算探地雷達功率譜參數與含水率之間的相關系數R1(表3)。

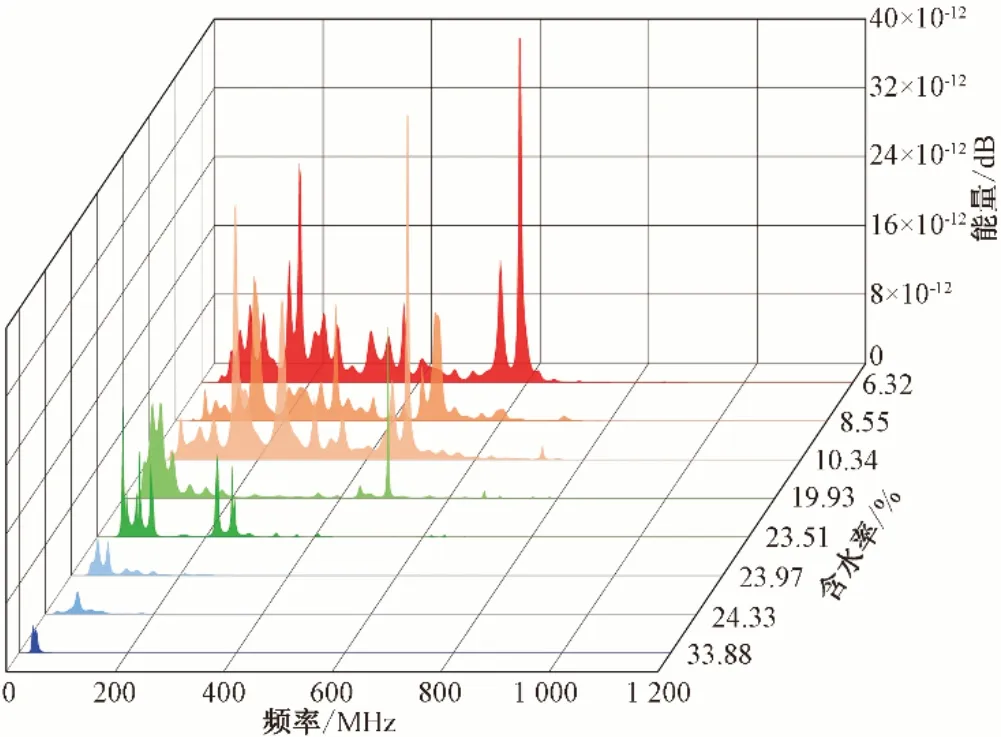
圖2 物理實驗400 MHz探地雷達功率譜圖Fig.2 Power spectral diagram of 400 MHz ground penetrating radar for physical experiment

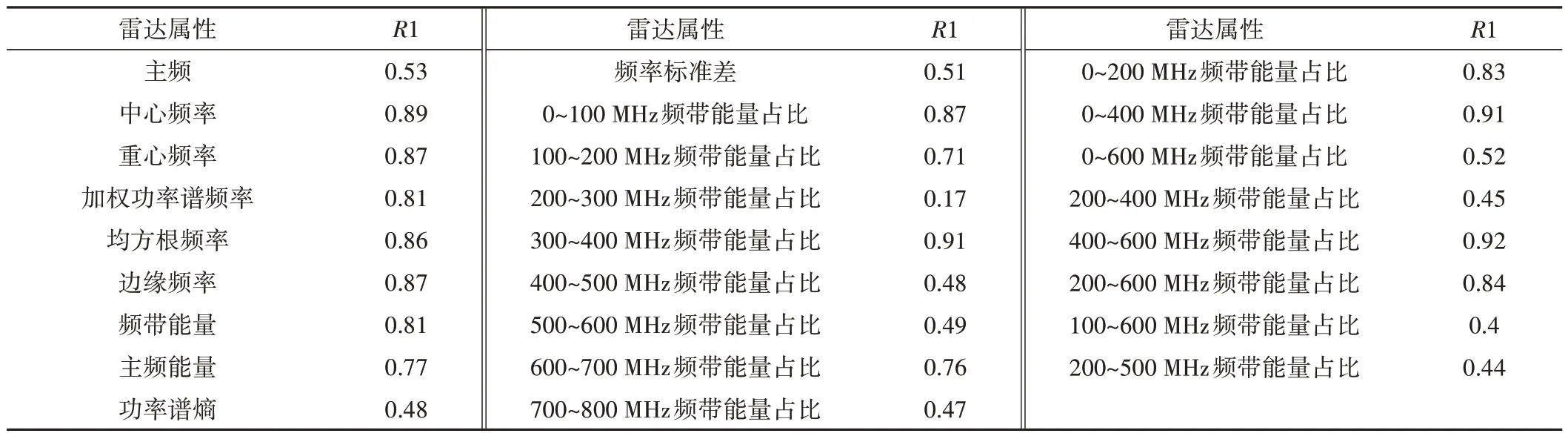
表3 物理實驗(R1)功率譜屬性參數與含水率相關系數Tab.3 Physical experiment (R1): correlation coefficients between power spectral attributes parameters and moisture content

如圖2 所示，圖中橫坐標為頻率(MHz)，縱坐標為含水率(cm3/cm3)，垂坐標為能量(dB)。從圖2 中可以看出在天線為400 MHz 的功率譜中，其功率分布的頻帶主要在0～800 MHz，其功率能量主要分布在0～20×10-12dB 范圍內；隨著土壤含水率的增高，探地雷達信號的功率譜能量逐漸降低；功率譜的能量分布頻帶逐漸向低頻偏移；功率譜能量分布逐漸聚集；功率譜曲線更加簡單；并且功率譜隨著土壤含水率的增加，低頻的能量占比也逐漸升高。

從表3中可以看出物理實驗中的探地雷達功率譜屬性參數中聚合程度屬性參數與土壤含水率相關性下降程度較快，頻率屬性參數和能量分布屬性參數與土壤含水率相關性受探測條件影響較小。從表3中可看出，與土壤含水率相關關系大于0.3的屬性參數個數為25個，但提取出來的探地雷達屬性之間并不一定互相獨立，為優化選擇與含水率相關性大且屬性之間相關性較小的功率譜屬性參數，采用互相關法對功率譜屬性參數進行優化選取。按照統計學中的定義，相關系數R介于0.75～1.00 兩者呈強相關性，介于0.3～0.7 兩者呈中等相關，考慮到計算精度、屬性類別及空間冗余程度的影響，選擇與含水率相關系數大于0.5 的功率譜屬性進行互相關，其互相關關系如圖3所示。

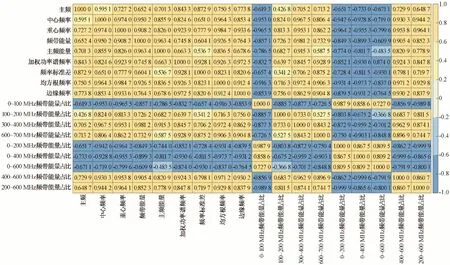
圖3 400 MHz功率譜屬性參數互相關熱力圖Fig.3 Thermographic map of cross-correlation of power spectral attribute parameters at 400 MHz

從圖3中可看出，表征雷達功率譜頻率的屬性參數：中心頻率、重心頻率、加權功率譜頻率和均方根頻率的互相關系數均大于0.8，且呈顯著正相關關系；表征雷達功率譜能量的屬性參數：頻帶能量和主頻能量的互相關系數為0.963，呈顯著正相關關系；表征雷達功率譜能量各頻帶占比屬性參數：0～100、0～200、0～400、0～600 MHz 頻帶能量占比相關系數均大于0.7，呈顯著正相關關系，300～400 和200～600 MHz 頻帶能量占比相關系數大于0.7，呈顯著正相關關系，600～700 和400～600 MHz 頻帶能量占比相關系數為0.897，呈0.01 水平的顯著正相關關系。對上述呈顯著正相關關系的屬性參數結合與含水率的相關關系選取優化，選出主頻、重心頻率、邊緣頻率、頻帶能量、頻率標準差、0～400 MHz 頻帶能量占比、400～600 MHz 頻帶能量占比等7 項功率譜屬性參數作為探地雷達功率譜特征屬性參數計算土壤含水率。

2.2 BP神經網絡預測土壤含水率結果

2.2.1 基于功率譜屬性與BP神經網絡的土壤含水率定性識別

首先通過塑、液限實驗測得貴陽市紅黏土液限為53.3%,塑限為30.58%，因此選定含水率30%為土壤含水率富水界限。然后引入混淆矩陣及相關性能評價指標對神經網絡識別土壤富水精度進行評價，混淆矩陣[20-22]是將分類模型中識別正確和錯誤的樣本進行統計，放入矩陣中表現出來。

如表4 所示，TP 為正類識別為正類的個數、TN 為負類識別為負類的個數、FN 為正類識別為負類的個數、FP 為負類識別為正類的個數。除此之外，精確率、召回率、特異度、準確率、曲線下面積和F1 值也能從另一個方向衡量分類模型的性能，表5對各個指標進行了簡單介紹。

表4 二值分類混淆矩陣Tab.4 Confusion matrix for binary classification

表5 神經網絡性能評價指標介紹Tab.5 Introduction to performance evaluation metrics for neural networks

根據2.2 物理實驗功率譜屬性參數互相關分析結果，選擇400 MHz天線中的功率譜屬性參數：主頻、重心頻率、邊緣頻率、頻帶能量、頻率標準差、0～400 MHz頻帶能量占比、400～600 MHz 頻帶能量占比等7 個功率譜屬性參數作為神經網絡的輸入樣本，輸出層有2個節點用于判斷土壤是否富水。

選取物理模型實驗中土壤含水率小于30%的7 組模型中60 道雷達信號，大于30%含水率模型中120 道雷達信號，共計540道信號計算其功率譜特征參數，并將其作為含水率雷達功率譜參數樣本庫，隨機選取功率譜參數樣本的70%作為模型訓練樣本，30%作為模型測試樣本進行土壤富水性識別。通過持續地學習過程中對神經網絡參數的調整，發現網絡的隱含層數、隱含層節點數、學習效率及訓練次數分別為3 層、10 個節點、學習效率0.15 及訓練30 000 次時，得出BP 神經網絡識別富水體模型效果最佳，其混淆矩陣與評價指標見圖4和表6。

表6 神經網絡性能評價Tab.6 Performance evaluation of neural networks

從圖4 和表6 可看出，神經網絡模型對非富水土層的召回率為100%，對富水土層的特異度分別為83.3%，對于非富水土層的精確率分別為95.5%，總體樣本預測準確率分別為96.3%，表明神經網絡模型對土壤富水性的實測預測精度較高；就模型分類性能而言，F1 值為0.988，AUC 為0.99，證明模型分類可靠，預測能力極好，精度較高。總的來說BP 神經網絡可以滿足對于檢測土壤富水性的要求。

2.2.2 基于功率譜屬性與BP神經網絡的土壤含水率定量探測

將主頻、重心頻率、邊緣頻率、頻帶能量、頻率標準差、0～400 MHz 頻帶能量占比、400～600 MHz 頻帶能量占比作為BP 神經網絡的輸入層參數，輸出層有1 個節點用于反演土壤含水率。

在物理模型實驗所取得32 個土壤樣本，22 個用于訓練模型，10 個用于檢驗模型反演效果。通過湊試法不斷對隱含層維數、節點數、學習效率和終止條件進行調整，結果表明在隱含層數為3 層，節點數為6 個，學習效率為0.1，網絡訓練1 000次時，預測模型達到最優。

通過訓練成功的神經網絡模型對測試的10 組數據進行預測。圖5為網絡輸出回歸分析線，反演土壤含水率與實際含水率的相關系數達0.936，表明模型輸出含水率與實際含水率接近。圖6 為BP 神經網絡反演與實測含水率比較圖，其中反演含水率與實際含水率的平均絕對誤差為1.25%，最大絕對誤差為2.6%，最小絕對誤差為0.07%，均方根誤差RMSE 為0.015。表明反演結果較好，基于功率譜屬性參數與BP 神經網絡結合的方法能夠反映土壤含水率與探地雷達屬性之間的非線性關系。

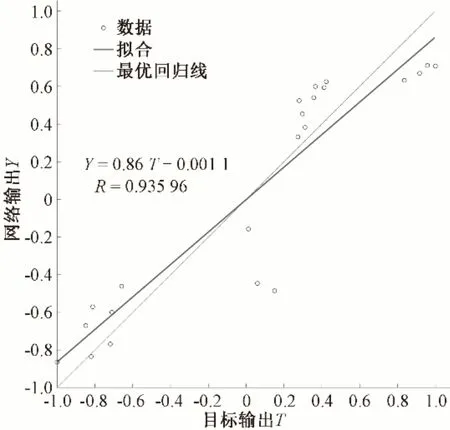
圖5 網絡輸出回歸分析線Fig.5 Regression analysis line of network output

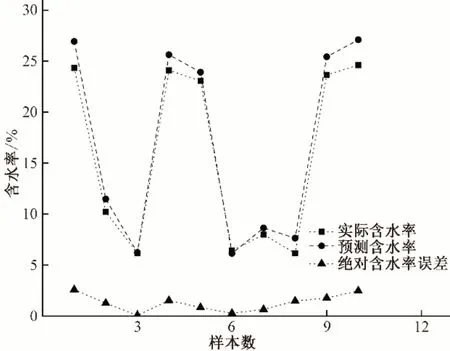
圖6 BP神經網絡反演與實測含水率誤差分析圖Fig.6 Error analysis plot of BP neural network inversion and measured water content in a physics experiment

2.3 實測驗證

在物理實驗結果分析及BP 神經網絡預測土壤含水率中，僅是采用整道探地雷達信號研究利用功率譜預測土壤含水率的可行性，為實現利用功率譜預測不同深度上土壤含水率。首先利用時窗選取壓縮變換技術截取0～80 cm 范圍內的探地雷達信號，約24 ns，并將信號設置為1 024個數據點；然后采用滾動時間窗剖面技術將信號分為8 段，每段128 個數據點，每段時窗長度及深度范圍分別為3 ns 及10 cm；最后利用AR 功率譜方法計算各深度上的探地雷達功率譜屬性參數。將野外實驗得到的探地雷達功率譜屬性參數作為測試樣本集，利用物理模型訓練出的BP 神經網絡對野外探測的土壤含水率進行識別與探測。并將BP 神經網絡中得出預測結果與烘干法比較，驗證結果如表7所示。

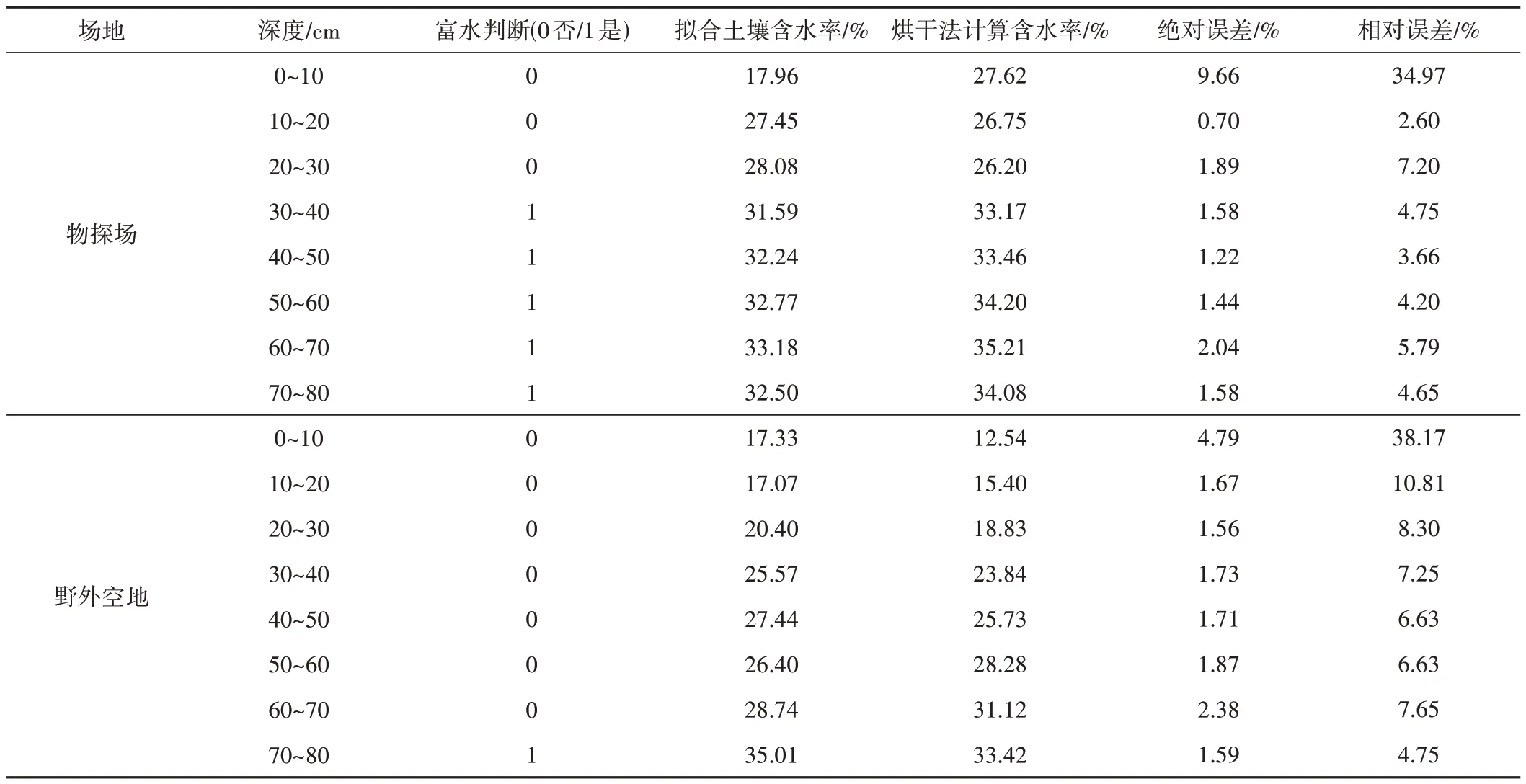
表7 野外實驗探地雷達功率譜屬性結合BP神經網絡土壤含水率擬合對照表Tab.7 Comparison table of soil moisture estimation using field experiments, ground-penetrating radar power spectrum attributes, and BP neural network

在物探場及野外空地的16 組土壤含水率富水性識別中，出現一次錯誤，整體來說利用功率譜屬性參數結合神經網絡能成功的識別土層富水性。功率譜屬性參數結合神經網絡識別土壤含水率的方法均在0～10 cm的誤差較大。10～80 cm范圍內400 MHz 和900 MHz 絕對誤差和相對誤差分別在3%和10%以內，可以看出利用功率譜屬性參數結合BP 神經網絡方法反演土壤含水率精度較高。

3 結 論

（1）基于物理模型獲取了不同含水率探地雷達信號，以AR 功率譜為理論模型獲取雷達功率譜并提取了雷達功率譜屬性參數，通過功率譜屬性參數與含水率之間的相關關系研究發現：土壤含水率增加會導致探地雷達功率譜能量頻帶向低頻偏移，低頻帶能量占比增加，高頻帶能量占比減少，能量分布聚合程度增強。

（2）采用屬性優化算法選出400 MHz天線的功率譜屬性參數，包括主頻、重心頻率、邊緣頻率、頻帶能量、頻率標準差、0～400 MHz頻帶能量占比和400～600 MHz頻帶能量占比作為反演土壤含水率的功率譜屬性參數。

（3）基于優選功率譜屬性參數結合BP 神經網絡方法對土壤含水狀態進行識別和探測，該方法對土壤含水狀態識別的準確率為96.3%；在對土壤含水率的探測中，反演結果與實際含水率的相關系數為0.936，平均絕對誤差為1.25%，均方根誤差RMSE為0.015。

（4）在野外實測中，對16 組土壤含水率進行富水性判別中出現1次失誤；物探場和野外空地土壤含水率探測土壤含水率的絕對誤差和相對誤差分別在3%、10%范圍內。結果表明利用功率譜屬性參數結合BP 神經網絡反演得到的土壤含水率較為精確，對于農業生產、土地復墾中的土壤含水率探測具有重要指導意義。