基于頂點輪廓的魯棒性抗前景干擾穩像算法

尹麗華,康 亮,劉士建

(1. 上海第二工業大學,上海 201209;2. 中國科學院上海技術物理研究所中國科學院紅外探測與成像技術重點實驗室,上海 200083)

1 引言

利用手機、數碼相機等設備拍照時,視頻抖動的存在不僅會影響視覺效果,而且容易影響各種后續的計算機視覺任務,例如,目標識別或跟蹤精度。因此,視頻穩像技術至關重要。目前該技術面臨如下的難點:如何處理有視差變化或運動前景干擾下的視頻,同時保證穩像精度。

根據所采用運動模型[1]不同,目前電子穩像方法主要歸為三類:2D、3D和2.5D方法。其中,2D模型最為簡單,通常是利用單個仿射模型來表示幀間的運動,并通過各種濾波方法平滑相機路徑。為了解決視差變化的穩像難題,Liu提出了基于捆綁相機路徑的模型[2],通過捆綁模型來替代單個模型。后來,于文杰又提出基于多路徑優化的穩像方法[3],通過對圖像進行網格劃分結并采用多路徑優化策略實現穩像,但是當特征點受遮擋時,該算法的穩像效果會受到限制。3D方法是利用復雜的三維重建實現穩像,該方法雖能處理視差問題,但是復雜度較高,實時性較差。通常2D和3D方法需要依賴于長特征軌跡的跟蹤,后來結合2D和3D方法的優勢,很多學者又提出2.5D方法[4-6],該方法避免了脆弱的特征跟蹤,Liu 在二維特征軌跡上應用低秩子空間約束[4],后來又利用極間轉移技術增加特征軌跡的長度,但該方法在復雜場景視頻中并不成立,比如擁堵的交通道路場景和密集的人流[5]。

為了解決運動前景干擾的難題,Shene曾提出將SURF算法和隨機抽樣一致性(RANSAC)算法相結合剔除異常點[7],但該算法只能剔除部分的前景特征點。后來,朱娟娟又提出基于三幀差分的穩像算法[8],該算法對簡單場景的效果較好,但不適用于大范圍前景的情況;謝亞晉等提出基于最小生成樹與改進卡爾曼濾波器的視頻穩像方法[9],提高了穩像精度,該算法當處理復雜前景干擾時的效果有限;Wu結合RANSAC和K-means聚類方法進行前景剔除[10],但該方法只適用于含大范圍運動前景的情況。后來,北京理工大學的楊佳麗結合陀螺儀數據進行運動估計,利用李群流形上的卡爾曼濾波進行平滑[11],但是穩像精度很容易受陀螺儀設備精度的限制。后來,Liu等提出SteadyFlow算法[12],屬于2.5D方法,用像素輪廓代替特征軌跡,但計算效率較低。在文獻[13]中,Zhao又提出綜合利用前景和背景的特征軌跡實現視頻的穩定,該算法雖提高了交通場景下的穩像精度,但對復雜場景的適用性則較差。另外,近年來深度學習技術在計算機視覺任務中也取得了巨大進步[14-16],比如在穩像方面,Wang等人提出第一個StabNet深度學習穩像網絡[14],該網絡根據輸入的抖動視頻序列學習一組抖動視頻到穩定視頻的映射。XU等人提出使用生成對抗網絡進行視頻穩像[15],屬于監督式的學習,上述兩種方法都需要用到大量的穩像視頻對數據集,獲取難度較大,而且實時性較差,不能滿足工程應用的需求。

綜上可知,目前的穩像方法主要適用于簡單場景,在當處理有大范圍和多運動前景干擾的情況時,仍有一定的局限性[17]。因此,結合2.5D方法的優勢,本文提出一種基于頂點輪廓的魯棒性抗前景干擾穩像方法,該算法的創新性主要體現在:首先,用頂點輪廓代替像素輪廓和特征軌跡,根據運動矢量的相似性生成了基于網格頂點的稀疏運動矢量,剔除了運動前景的干擾,同時提高了算法的效率;其次,利用時間分析法識別出具有不連續運動矢量的網格頂點,并通過中值濾波器f2對網格頂點處的運動矢量補全,進一步剔除了復雜運動前景的干擾。

2 算法原理

本算法的流程如圖1所示。

算法流程描述如下:

1)對輸入視頻檢測FAST特征[18]。

2)生成稀疏運動矢量。將圖像劃分為m×n網格,利用基于金字塔的Lucas-Kanade光流算法得到特征匹配對;并根據運動矢量的相似性,利用中值濾波器f1生成基于網格頂點的稀疏運動矢量。

3)稀疏運動矢量的空間平滑。為了能有效剔除復雜運動前景的干擾,本文先通過時間分析法識別出具有不連續運動矢量的網格頂點,并剔除“離群”頂點對應的運動矢量;并利用中值濾波器f2對網格頂點處的運動矢量補全,實現運動矢量的空間平滑。

4)對不同時刻基于網格的運動矢量進行累加,形成頂點輪廓。

5)通過路徑平滑策略,對頂點輪廓進行平滑。

6)對圖像進行反向補償,輸出穩定視頻。

2.1 生成基于網格頂點的稀疏運動矢量

將圖像劃分為m×n的網格,利用基于金字塔的Lucas-Kanade(簡稱LK)算法[19]得到特征匹配對,計算部分特征點的運動矢量;然后,利用中值濾波器f1將已知運動矢量擴展到它附近的網格頂點,得到網格頂點的運動矢量,并用它生成頂點輪廓。

本算法利用采用頂點輪廓,而非像素輪廓和特征軌跡。下圖2給出了特征軌跡、像素輪廓、頂點輪廓的對比,其中,圖2(a)代表特征軌跡,該特征軌跡由第t-1幀中特征點像素A->第t幀中的對應像素B->第(t+1)幀中的對應像素C構成,由于運動前景的存在,獲取長特征軌跡的難度較大。圖(b)代表像素輪廓,是同像素點在一段時間內的運動矢量構成,該方法需要收集所有像素點的運動矢量,因此計算效率比較低;圖(c)代表頂點輪廓,僅收集每個網格頂點處的運動矢量,不僅能避免脆弱的特征的跟蹤,而且相對于像素輪廓,因此,頂點輪廓的運算效率能得到提高。

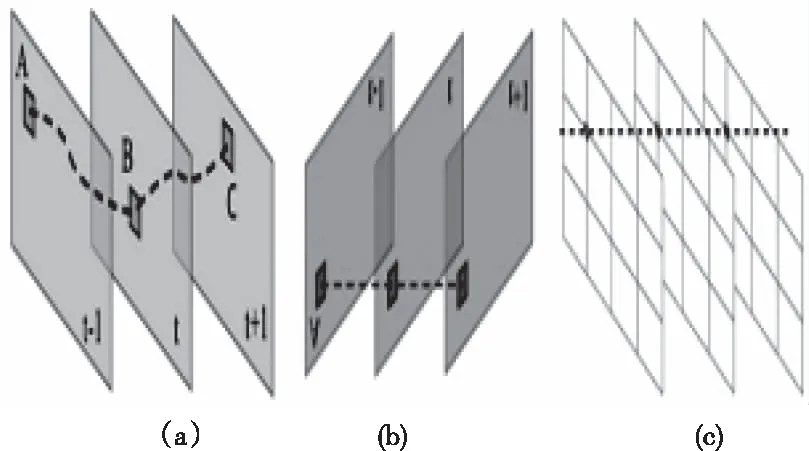
圖2 特征軌跡、像素輪廓、頂點輪廓的對比

2.1.1 FAST特征匹配

利用基于金字塔的Lucas-Kanade光流算法通過由粗到精的搜索策略實現特征匹配。在圖像J中找到圖像I中特征點μ所對應的特征點ν,匹配過程的描述如下:

a) 對圖像I和圖像J建立高斯金字塔。

c) 根據上層計算結果,并利用迭代計算(L-1)層的殘差光流向量d(L-1);

d) 接著,估計(L-1)層的光流量:

gL-1=2(gL-1+dL)

(1)

e) 重復步驟(c) (d),直至L=0,估計出最終光流f=g0+d0,最終,在圖像J中找到圖像I中特征點μ所對應的特征點ν,即ν=μ+f。

2.1.2 運動矢量的擴展

運動矢量擴展的過程如圖3所示。

圖3 運動矢量擴展的示意圖

Step1:首先,利用FAST特征點對的匹配結果,計算各個特征點所對應的運動矢量。

如圖(a)所示,圖中{p,p′}代表第t幀和第t-1幀中的FAST特征點匹配對,紅點代表特征點位置,虛線箭頭代表運動矢量,則特征點p處所對應的運動矢量vp為

vp=p′-Ftp

(2)

式中:Ft表示全局單應性矩陣。

Step2:以特征點p為中心,建立一個r1×r1圓形模板,如圖(b)所示。

Step3:根據運動矢量的相似性,采用中值過濾器f1,將該過濾器的響應分配給圓形模板中其它的網格頂點,如圖(c)所示。由于所有匹配的特征都會將運動矢量傳播到其附近的網格頂點,因此,同一個網格頂點可能接收多個運動矢量。本文中采用中值過濾器f1,將過濾器的響應被分配給網格頂點。對第t幀圖像,網格頂點q的運動矢量ut(q)為

ut(q)=med{vp,p∈Ωq}

(3)

式中,Ωq表示網格頂點附近位于它r1×r1圓形模板內的所有特征點。

圖4為利用中值濾波器f1對網格頂點運動矢量估算的示例。圖中,紅色“○”表示特征點,網格頂點(藍色☆)受到多個運動矢量的影響。

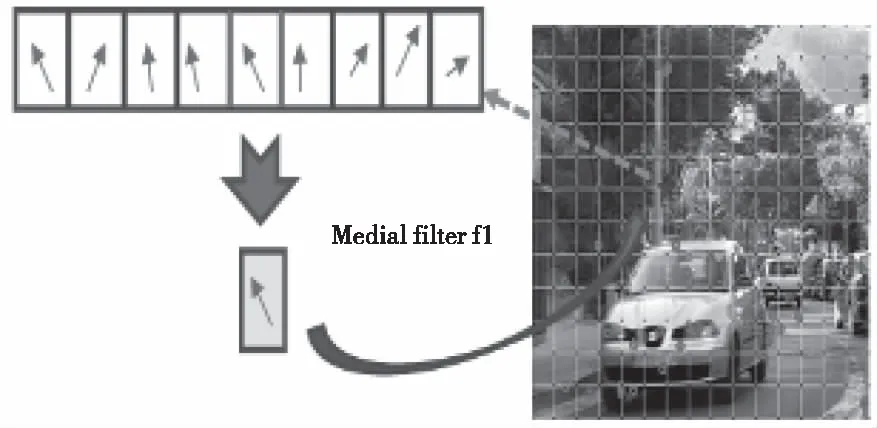
圖4 利用中值濾波器f 1對網格頂點運動矢量估算的示例

2.2 稀疏運動矢量的空間平滑

受復雜運動前景干擾的影響,圖像的稀疏運動矢量往往不連續,直接補償會導致穩像后圖像出現“渲染”偽像。因此,需要剔除復雜運動前景的干擾。本文中提出對運動矢量進行空間平滑,先通過時間分析法,識別出具有不連續運動矢量的網格頂點,剔除“離群”頂點對應的運動矢量;并利用中值濾波器f2對頂點處的運動矢量補全,實現平滑。

2.2.1 時間分析法

對于第t幀圖像,網格頂點q處的運動矢量Wt(q)是對多組運動矢量ut(q)進行累加得到的結果,具體的定義如下

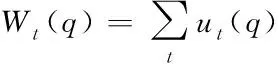
(4)

式中:ut(q)為頂點q在第t幀的運動矢量。

時間分析法基于如下假設:對包含背景和運動前景的運動軌跡,背景區域內頂點的累積運動矢量Wt(q)在時間上通常應該是平滑的,而運動前景區域內的網格頂點的累積運動矢量Wt(q)在時間上往往具有不連續性。

因此,本算法中通過判斷累積運動矢量的軌跡是否在時間上光滑識別不連續運動矢量,同時,使用掩模Mt(q)來記錄第t幀圖像中的頂點q是否離群,Mt(q)定義如下

(5)

式中,G為高斯濾波器(默認的標準偏差為3),如果離群,則令Mt(q)=0,否則令Mt(q)=1。

2.2.2 運動矢量的補全策略

形成離群點掩模后,需要更新并補全對應頂點處的運動矢量,并分以下兩種情況:

第一種:如果Mt(q)=1,則該網格頂點處的運動矢量仍然保持不變。

第二種:如果Mt(q)=0,剔除將該網格頂點處的運動矢量,并利用中值濾波器f2對該點處的運動矢量進行補全。以頂點q為中心,通過r2×r2的方形模板進行覆蓋,則最終運動矢量為中值濾波器的響應,公式如下

ut(q)=med{ut(k),k∈Wq},WhenMt(q)=1

(6)

式中,Wq表示以網格頂點q為中心,位于附近它附近r2×r2方形模板內的所有頂點。

運動矢量空間平滑的示例如圖5所示,其中,圖(a)表示原始運動矢量,圖(b)為識別出運動前景上的網格頂點,圖(c)為運動矢量平滑后的局部效果圖,從圖中可以看出,本算法能有效識別出運動前景,剔除前景的干擾。

圖5 運動矢量空間平滑的示例

2.3 生成頂點輪廓

在頂點輪廓生成之前,為了保證算法的魯棒性,本文算法中先使用全局單應性Ft為所有頂點得到全局運動矢量場Vt,則第t幀圖像中第i個網格頂點對應的最終運動矢量y為ut′(i)=Vt(i)+ut(i)。

第t幀圖像中第i個網格頂點的頂點輪廓Ct(i)是通過對所有時間點的運動矢量累加得到,即

(7)

式中:ut(i)為第t幀圖像中第i個網格頂點所對應的運動矢量,相同方法可得到其它頂點輪廓。

圖6為不同位置網格頂點處的運動軌跡對比,從前、后三幀圖像中抽出兩個特殊網格頂點處位置,頂點1位于背景上,頂點2位于運動前景上。圖(a)中頂點1用☆表示,網格頂點2用○表示,不同時刻用紅色、綠色、藍色來區別。

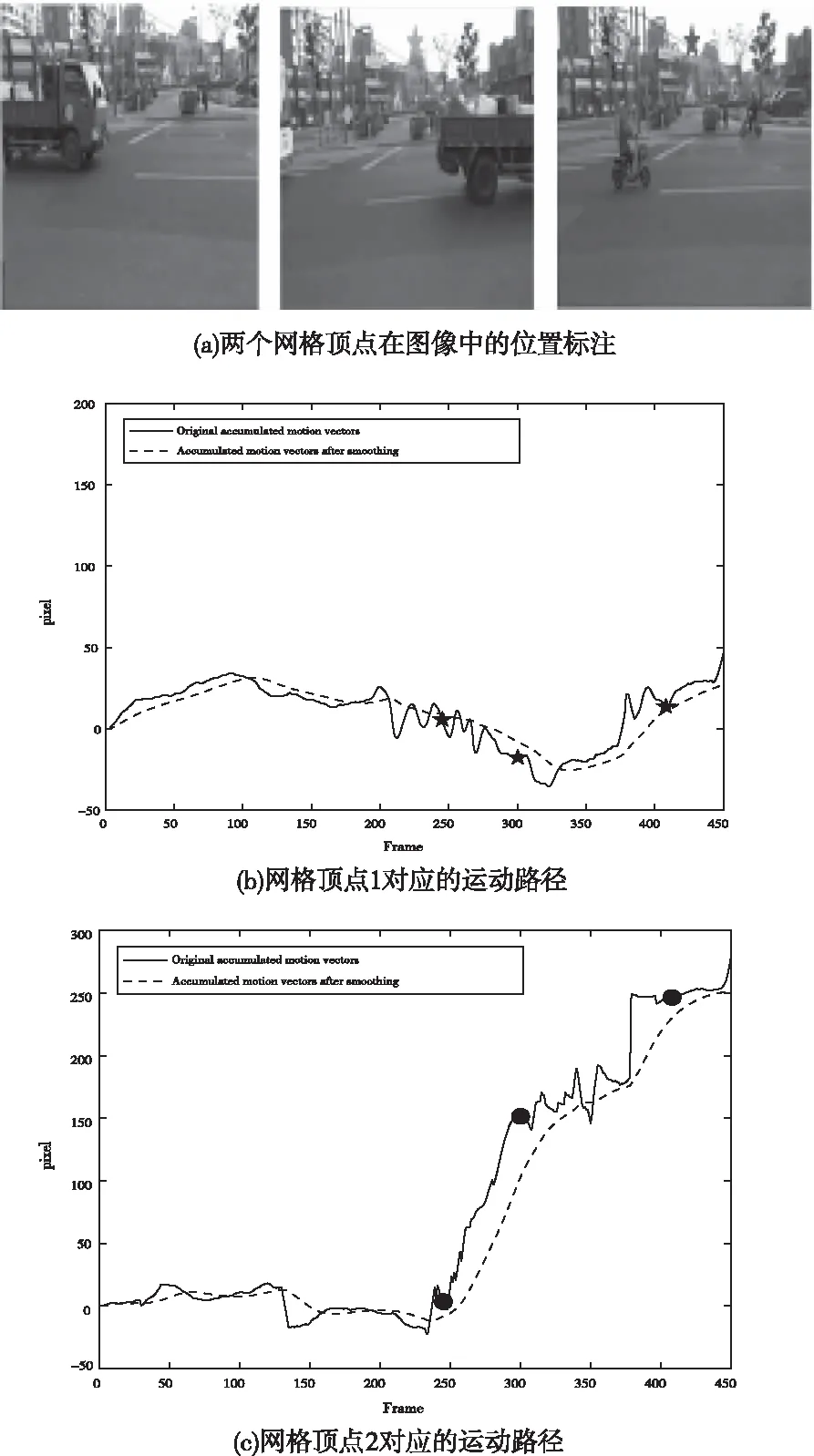
圖6 不同網格頂點處的運動路徑對比

圖(b)為網格頂點1對應的運動路徑,圖(c)為網格頂點2對應的運動路徑。由圖(b)的運動曲線可以看出,頂點1始終位于靜態背景上,所以它的累積運動向量在時間上是存在少量的高頻分量,處理后的路徑也更加平滑。由圖(c)的運動曲線可以看出,頂點2位于運動前景上,由于有移動的車輛經過,未平滑前運動曲線時具有大量的高頻分量,經平滑后的運動曲線,剔除了高頻分量,真正起到了抗前景干擾的作用。

2.4 基于頂點輪廓的穩定

為了路徑的優化,希望避免出現過度的裁剪以及穩定化后的扭曲問題,采用最小化目標函數來實現頂點輪廓的平滑

(8)

其中,頂點輪廓Ct為原始路徑,希望的是得到最優路徑Pt,P和C均是非參數的累積運動向量。

3 結果與討論

為了能有效說明該算法的優勢,本文實驗主要從以下三個方面展開:首先,從數據集中選出受大范圍和多個運動前景干擾下的視頻進行穩像實驗;其次,從數據集中選出六組含運動前景、視差變化、旋轉或縮放的視頻進行穩像實驗,驗證算法的魯棒性;最后,將本文算法和傳統算法的實時性進行了對比。

另外,本文的驗證實驗均是在硬件環境為 Intel(R) Core(TM)i5-5200U CPU@2.20GHZ,8GB內存,64位Win10的系統上進行的,采用Python3.8.6軟件平臺,并依賴Opencv圖像處理庫以及CVX安裝包。

3.1 受大范圍和多運動前景干擾下的穩像結果

從多個公共數據集[20,21]中選出復雜前景干擾下的兩組測試視頻,如下圖7所示,圖(a)為受大范圍運動前景干擾的視頻組,圖(b)為受多個運動前景干擾的視頻組。

圖7 復雜前景干擾下的兩組測試視頻

為了說明本文算法對于復雜前景干擾下視頻的穩像優勢,分別采用傳統穩像算法Liu[2]、Wu[10]、Zhao[13]和本文算法進行穩像,并計算出兩組視頻下采用各算法后的峰值信噪比(PSNR),兩組視頻下的PSNR結果分別如下表1、表2所示,表1為受大范圍運動前景干擾下的PSNR值,表2為受多個運動前景干擾下的PSNR值。

表1 大運動前景干擾下視頻的PSNR值

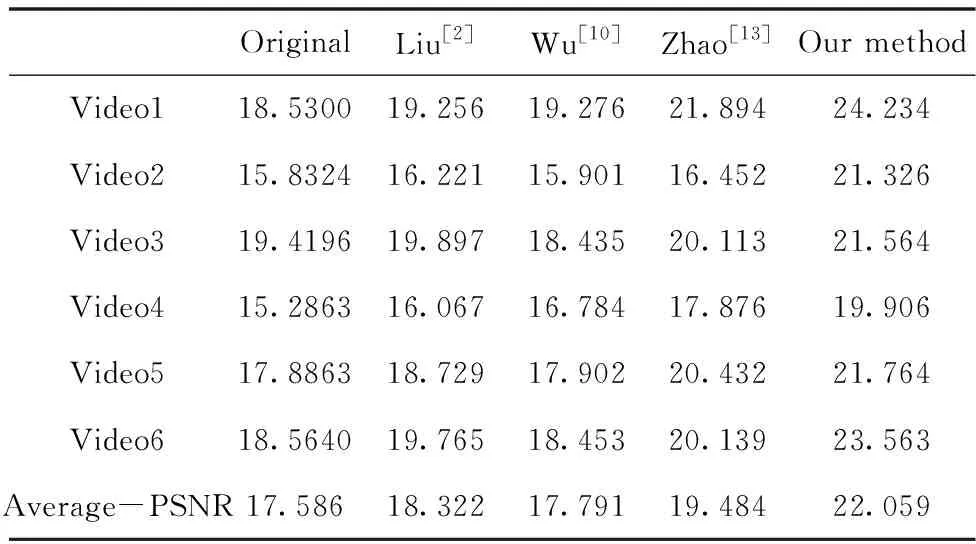
表2 多運動前景干擾下視頻的PSNR值

峰值信噪比(PSNR)常用來衡量視頻的穩像質量好壞,主要反映了參考圖像和當前圖像間的峰值信噪比,定義如下

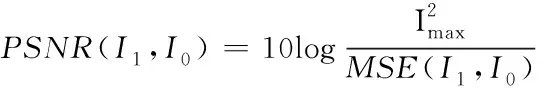
(15)

式中,Imax是最大亮度值,MSE(I1,I0)表示連續幀間的均方差。PSNR值越大,則說明幀間的灰度差越小,圖像穩定的效果越好。

由表1可以看出,在大運動前景干擾下,本文算法的平均PSNR值為27.871,比三種傳統的算法Liu[2]、Wu[10]、Zhao[13]的PSNR值提高更明顯,與近年的Zhao[13]算法相比,PSNR值提高了14.9%(即(27.871-24.254)/24.254*100%=14.9%)。由表2可以看出,在多運動前景干擾下,本文算法的平均PSNR值為22.059,比三種傳統算法Liu[2]、Wu[10]、Zhao[13]的PSNR值提高更明顯,與近年的Zhao[13]算法相比,PSNR值可以提高13.2%(即:(22.059-19.484)/19.484*100%=13.2%)。

因此,綜合表1、表2中的數據可以看出結論,在復雜運動場景的干擾下,本算法比傳統算法PSNR值提高更明顯,更具有穩像優勢。

另外,為了能直觀比較各算法的穩像效果,下圖(8)、和圖(9)分別為受大范圍、多個運動前景干擾下的穩像結果,其中,圖(a)為原始圖像幀,圖(b)為Zhao[13]算法的穩像結果,圖(c)為本文算法的穩像結果。

通過圖8(b)、圖8(c)的結果對比,可以看出經本算法穩像后的圖像邊緣區域更少,視頻過渡更加平滑,視覺效果更好,這說明本文算法不僅能更好的剔除大范圍運動前景的干擾。通過圖9(b)、圖9(c)的結果對比,可以看出,本算法對多個運動前景干擾的情況也能實現不錯的視覺穩像結果。

圖8 受大運動前景干擾下的視頻穩像結果

圖9 受多個運動前景干擾下的視頻穩像結果

3.2 驗證本文算法的魯棒性

從公共數據集中選出六組含運動前景、視差變化、旋轉或縮放的測試視頻進行實驗,驗證魯棒性的測試視頻如圖10所示。

圖10 驗證魯棒性的測試視頻

接下來,將本文算法與四種傳統穩像算法Subspace[4]、Epipolar[5]、Bundled-paths[2]、SteadyFlow[12]進行客觀評價指標的對比。評價指標分別采用:Cropping Ratio(裁剪率)、Distortion(失真率)、Stability(穩定度)。

圖11為各算法的穩像指標對比,通過對比可以看出,當處理包含運動前景、視差變化、旋轉或縮放的視頻時,本文算法相對于傳統算法,裁剪率、失真率和穩定度三個指標方面表現較好,充分說明該算法具有魯棒性。

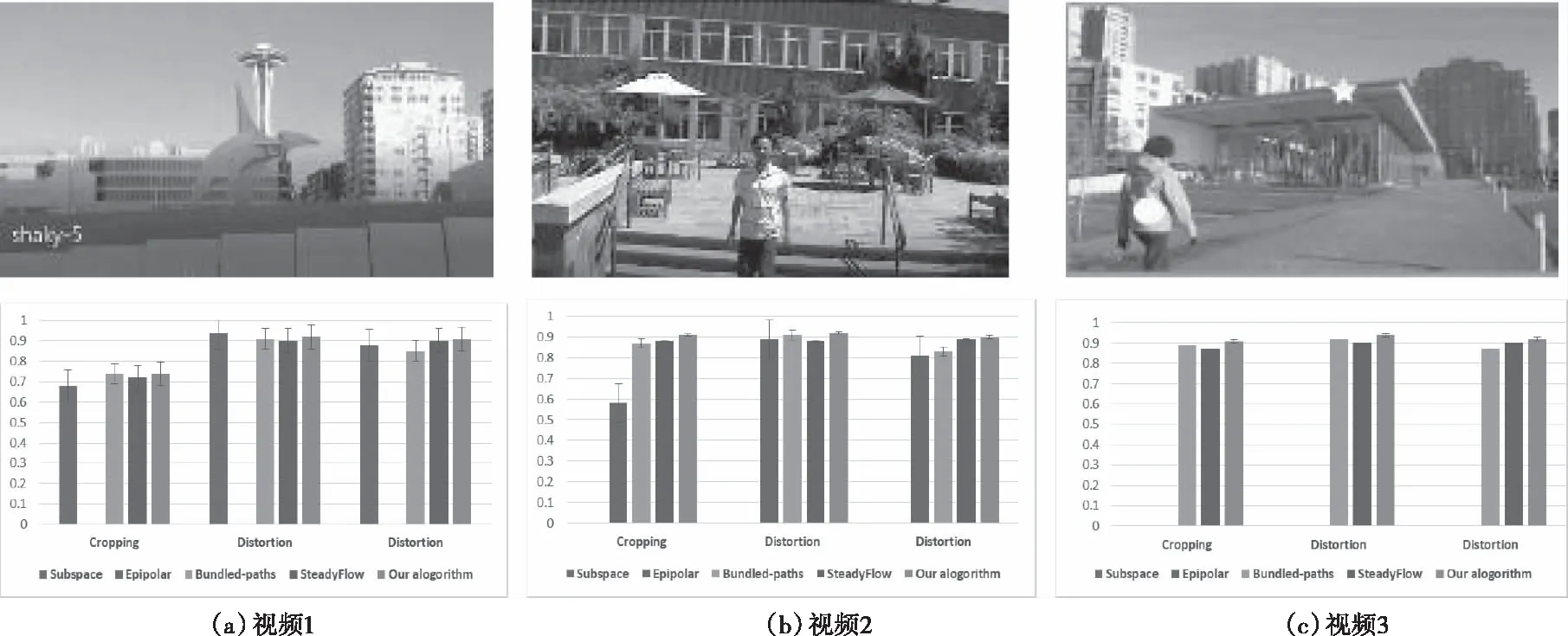
圖11 各算法的穩像指標對比

3.3 運行時間比較

從數據集中選取出分辨率為720×1280,360×640,480×272的三組測試視頻,視頻中均包含了復雜運動前景,本文中分別采用了SteadyFlow[12]、Zhao[13]和本文算法進行穩像實驗,各算法的運行時間結果如表3所示。

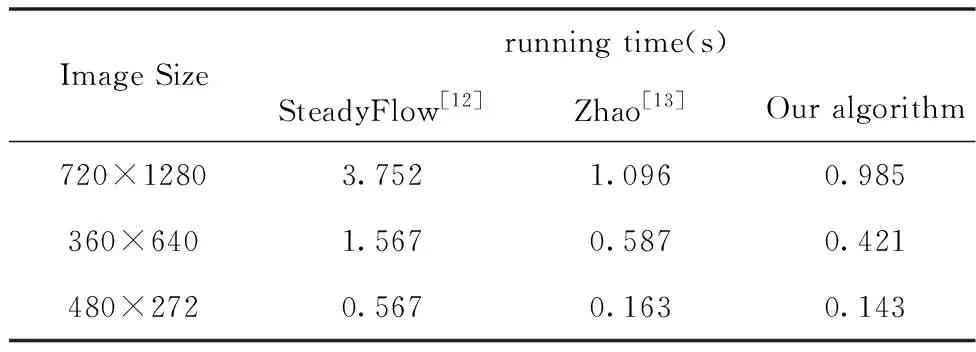
表3 各算法的運行時間結果

通過表3中各算法運行時間,可以看出,在三種不同圖像尺寸下,SteadyFlow算法[12]的運行時間分別約為本文算法運行時間的3.8倍、3.7倍、3.9倍,本算法的實時性更具優勢,主要是因為本算法僅需要收集每網格頂點處的運動矢量,運動矢量場稀疏化,因此運算效率得到明顯提高。另外,雖然本文算法與Zhao[13]算法相比,運行效率也得到一定程度的提高,但本文算法的穩像精度比Zhao算法[13]更高,本文算法的穩像精度和實時性能滿足工程應用的實際需求。

4 結論

為了解決復雜運動前景對穩像精度干擾的難題,本文提出一種基于頂點輪廓的魯棒性抗前景干擾穩像方法,實驗結果表明,該算法在裁剪率、失真率和穩定度三個指標方面表現較好,運算效率更高,更能滿足穩像算法的實時性要求。但本算法對于背景比較復雜的情況仍有一定局限性,需要后續進行深入研究。